动态规划帮我通关了《魔塔》
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
———–
「魔塔」是一款经典的地牢类游戏,碰怪物要掉血,吃血瓶能加血,你要收集钥匙,一层一层上楼,最后救出美丽的公主。
现在手机上仍然可以玩这个游戏:
嗯,相信这款游戏承包了不少人的童年回忆,记得小时候,一个人拿着游戏机玩,两三个人围在左右指手画脚,这导致玩游戏的人体验极差,而左右的人异常快乐 😂
力扣第 174 题是一道类似的题目,我简单描述一下:
输入一个存储着整数的二维数组 grid,如果 grid[i][j] > 0,说明这个格子装着血瓶,经过它可以增加对应的生命值;如果 grid[i][j] == 0,则这是一个空格子,经过它不会发生任何事情;如果 grid[i][j] < 0,说明这个格子有怪物,经过它会损失对应的生命值。
现在你是一名骑士,将会出现在最上角,公主被困在最右下角,你只能向右和向下移动,请问你初始至少需要多少生命值才能成功救出公主?
换句话说,就是问你至少需要多少初始生命值,能够让骑士从最左上角移动到最右下角,且任何时候生命值都要大于 0。
函数签名如下:
int calculateMinimumHP(int[][] grid);
比如题目给我们举的例子,输入如下一个二维数组 grid,用 K 表示骑士,用 P 表示公主:
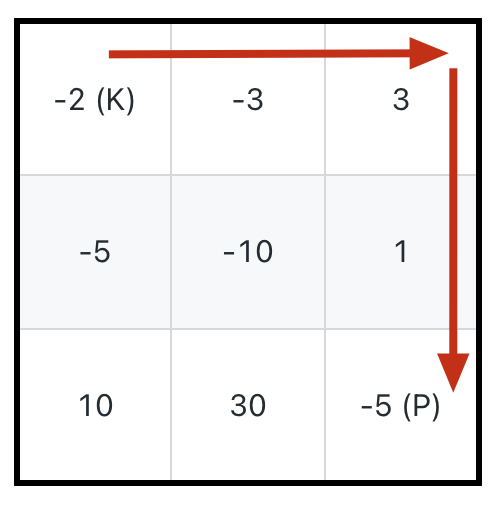
算法应该返回 7,也就是说骑士的初始生命值至少为 7 时才能成功救出公主,行进路线如图中的箭头所示。
上篇文章最小路径和写过类似的问题,问你从左上角到右下角的最小路径和是多少。
我们做算法题一定要尝试举一反三,感觉今天这道题和最小路径和有点关系对吧?
想要最小化骑士的初始生命值,是不是意味着要最大化骑士行进路线上的血瓶?是不是相当于求「最大路径和」?是不是可以直接套用计算「最小路径和」的思路?
但是稍加思考,发现这个推论并不成立,吃到最多的血瓶,并不一定就能获得最小的初始生命值。
比如如下这种情况,如果想要吃到最多的血瓶获得「最大路径和」,应该按照下图箭头所示的路径,初始生命值需要 11:
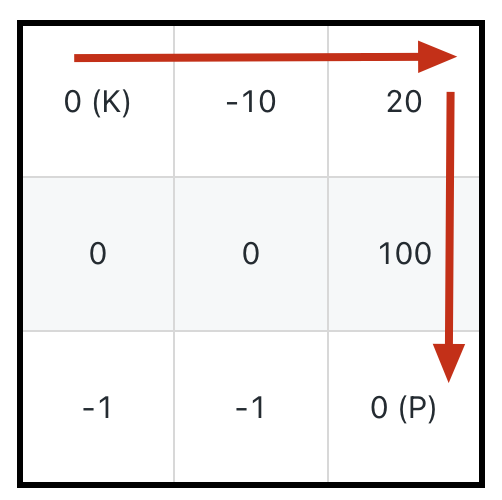
但也很容易看到,正确的答案应该是下图箭头所示的路径,初始生命值只需要 1:
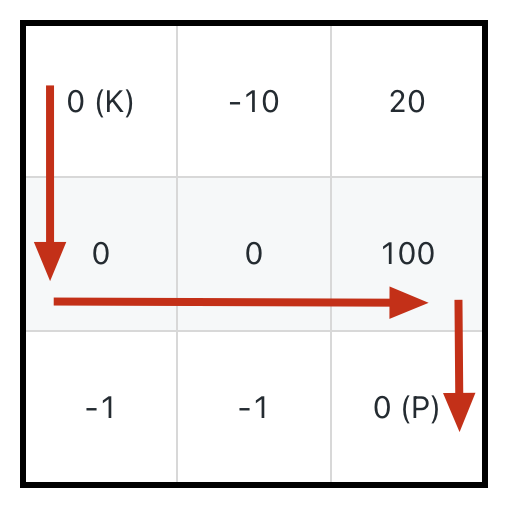
所以,关键不在于吃最多的血瓶,而是在于如何损失最少的生命值。
这类求最值的问题,肯定要借助动态规划技巧,要合理设计 dp 数组/函数的定义。类比前文最小路径和问题,dp 函数签名肯定长这样:
int dp(int[][] grid, int i, int j);
但是这道题对 dp 函数的定义比较有意思,按照常理,这个 dp 函数的定义应该是:
从左上角(grid[0][0])走到 grid[i][j] 至少需要 dp(grid, i, j) 的生命值。
这样定义的话,base case 就是 i, j 都等于 0 的时候,我们可以这样写代码:
int calculateMinimumHP(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
// 我们想计算左上角到右下角所需的最小生命值
return dp(grid, m - 1, n - 1);
}
int dp(int[][] grid, int i, int j) {
// base case
if (i == 0 && j == 0) {
// 保证骑士落地不死就行了
return gird[i][j] > 0 ? 1 : -grid[i][j] + 1;
}
...
}
PS:为了简洁,之后 dp(grid, i, j) 就简写为 dp(i, j),大家理解就好。
接下来我们需要找状态转移了,还记得如何找状态转移方程吗?我们这样定义 dp 函数能否正确进行状态转移呢?
我们希望 dp(i, j) 能够通过 dp(i-1, j) 和 dp(i, j-1) 推导出来,这样就能不断逼近 base case,也就能够正确进行状态转移。
具体来说,「到达 A 的最小生命值」应该能够由「到达 B 的最小生命值」和「到达 C 的最小生命值」推导出来:
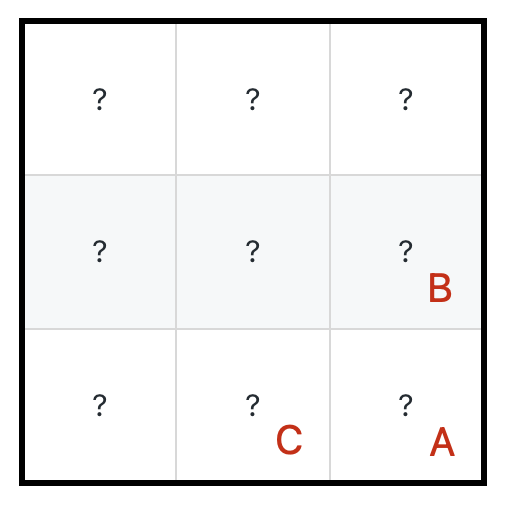
但问题是,能推出来么?实际上是不能的。
因为按照 dp 函数的定义,你只知道「能够从左上角到达 B 的最小生命值」,但并不知道「到达 B 时的生命值」。
「到达 B 时的生命值」是进行状态转移的必要参考,我给你举个例子你就明白了,假设下图这种情况:
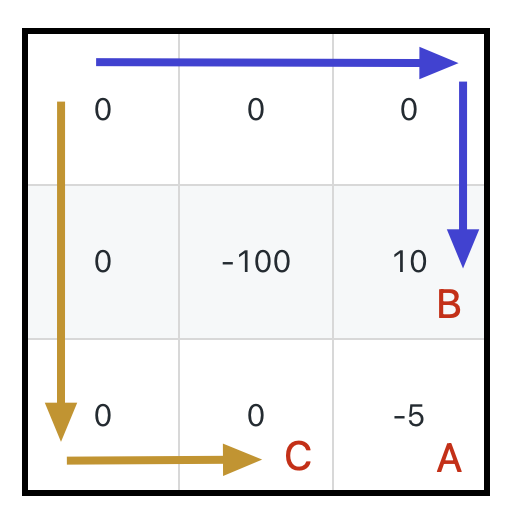
你说这种情况下,骑士救公主的最优路线是什么?
显然是按照图中蓝色的线走到 B,最后走到 A 对吧,这样初始血量只需要 1 就可以;如果走黄色箭头这条路,先走到 C 然后走到 A,初始血量至少需要 6。
为什么会这样呢?骑士走到 B 和 C 的最少初始血量都是 1,为什么最后是从 B 走到 A,而不是从 C 走到 A 呢?
因为骑士走到 B 的时候生命值为 11,而走到 C 的时候生命值依然是 1。
如果骑士执意要通过 C 走到 A,那么初始血量必须加到 6 点才行;而如果通过 B 走到 A,初始血量为 1 就够了,因为路上吃到血瓶了,生命值足够抗 A 上面怪物的伤害。
这下应该说的很清楚了,再回顾我们对 dp 函数的定义,上图的情况,算法只知道 dp(1, 2) = dp(2, 1) = 1,都是一样的,怎么做出正确的决策,计算出 dp(2, 2) 呢?
所以说,我们之前对 dp 数组的定义是错误的,信息量不足,算法无法做出正确的状态转移。
正确的做法需要反向思考,依然是如下的 dp 函数:
int dp(int[][] grid, int i, int j);
但是我们要修改 dp 函数的定义:
从 grid[i][j] 到达终点(右下角)所需的最少生命值是 dp(grid, i, j)。
那么可以这样写代码:
int calculateMinimumHP(int[][] grid) {
// 我们想计算左上角到右下角所需的最小生命值
return dp(grid, 0, 0);
}
int dp(int[][] grid, int i, int j) {
int m = grid.length;
int n = grid[0].length;
// base case
if (i == m - 1 && j == n - 1) {
return grid[i][j] >= 0 ? 1 : -grid[i][j] + 1;
}
...
}
根据新的 dp 函数定义和 base case,我们想求 dp(0, 0),那就应该试图通过 dp(i, j+1) 和 dp(i+1, j) 推导出 dp(i, j),这样才能不断逼近 base case,正确进行状态转移。
具体来说,「从 A 到达右下角的最少生命值」应该由「从 B 到达右下角的最少生命值」和「从 C 到达右下角的最少生命值」推导出来:
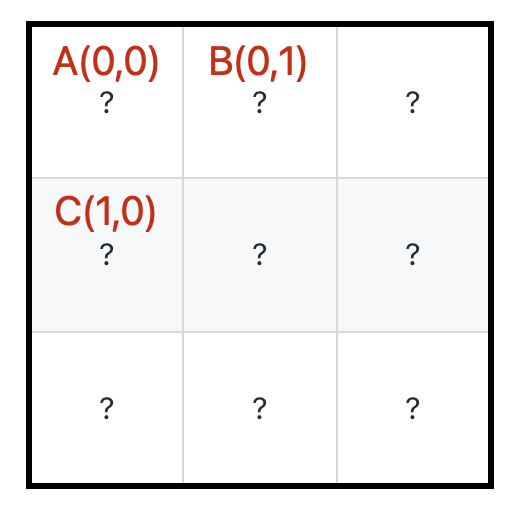
能不能推导出来呢?这次是可以的,假设 dp(0, 1) = 5, dp(1, 0) = 4,那么可以肯定要从 A 走向 C,因为 4 小于 5 嘛。
那么怎么推出 dp(0, 0) 是多少呢?
假设 A 的值为 1,既然知道下一步要往 C 走,且 dp(1, 0) = 4 意味着走到 grid[1][0] 的时候至少要有 4 点生命值,那么就可以确定骑士出现在 A 点时需要 4 - 1 = 3 点初始生命值,对吧。
那如果 A 的值为 10,落地就能捡到一个大血瓶,超出了后续需求,4 - 10 = -6 意味着骑士的初始生命值为负数,这显然不可以,骑士的生命值小于 1 就挂了,所以这种情况下骑士的初始生命值应该是 1。
综上,状态转移方程已经推出来了:
int res = min(
dp(i + 1, j),
dp(i, j + 1)
) - grid[i][j];
dp(i, j) = res <= 0 ? 1 : res;
根据这个核心逻辑,加一个备忘录消除重叠子问题,就可以直接写出最终的代码了:
/* 主函数 */
int calculateMinimumHP(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
// 备忘录中都初始化为 -1
memo = new int[m][n];
for (int[] row : memo) {
Arrays.fill(row, -1);
}
return dp(grid, 0, 0);
}
// 备忘录,消除重叠子问题
int[][] memo;
/* 定义:从 (i, j) 到达右下角,需要的初始血量至少是多少 */
int dp(int[][] grid, int i, int j) {
int m = grid.length;
int n = grid[0].length;
// base case
if (i == m - 1 && j == n - 1) {
return grid[i][j] >= 0 ? 1 : -grid[i][j] + 1;
}
if (i == m || j == n) {
return Integer.MAX_VALUE;
}
// 避免重复计算
if (memo[i][j] != -1) {
return memo[i][j];
}
// 状态转移逻辑
int res = Math.min(
dp(grid, i, j + 1),
dp(grid, i + 1, j)
) - grid[i][j];
// 骑士的生命值至少为 1
memo[i][j] = res <= 0 ? 1 : res;
return memo[i][j];
}
这就是自顶向下带备忘录的动态规划解法,参考前文动态规划套路详解很容易就可以改写成 dp 数组的迭代解法,这里就不写了,读者可以尝试自己写一写。
这道题的核心是定义 dp 函数,找到正确的状态转移方程,从而计算出正确的答案。