经典动态规划:最长公共子序列
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
———–
好久没写动态规划算法相关的文章了,今天来搞一把。
不知道大家做算法题有什么感觉,我总结出来做算法题的技巧就是,把大的问题细化到一个点,先研究在这个小的点上如何解决问题,然后再通过递归/迭代的方式扩展到整个问题。
比如说我们前文手把手带你刷二叉树第三期,解决二叉树的题目,我们就会把整个问题细化到某一个节点上,想象自己站在某个节点上,需要做什么,然后套二叉树递归框架就行了。
动态规划系列问题也是一样,尤其是子序列相关的问题。本文从「最长公共子序列问题」展开,总结三道子序列问题,解这道题仔细讲讲这种子序列问题的套路,你就能感受到这种思维方式了。
最长公共子序列
计算最长公共子序列(Longest Common Subsequence,简称 LCS)是一道经典的动态规划题目,大家应该都见过:
给你输入两个字符串 s1 和 s2,请你找出他们俩的最长公共子序列,返回这个子序列的长度。
力扣第 1143 题就是这道题,函数签名如下:
int longestCommonSubsequence(String s1, String s2);
比如说输入 s1 = "zabcde", s2 = "acez",它俩的最长公共子序列是 lcs = "ace",长度为 3,所以算法返回 3。
如果没有做过这道题,一个最简单的暴力算法就是,把 s1 和 s2 的所有子序列都穷举出来,然后看看有没有公共的,然后在所有公共子序列里面再寻找一个长度最大的。
显然,这种思路的复杂度非常高,你要穷举出所有子序列,这个复杂度就是指数级的,肯定不实际。
正确的思路是不要考虑整个字符串,而是细化到 s1 和 s2 的每个字符。前文子序列解题模板中总结的一个规律:
对于两个字符串求子序列的问题,都是用两个指针 i 和 j 分别在两个字符串上移动,大概率是动态规划思路。
最长公共子序列的问题也可以遵循这个规律,我们可以先写一个 dp 函数:
// 定义:计算 s1[i..] 和 s2[j..] 的最长公共子序列长度
int dp(String s1, int i, String s2, int j)
这个 dp 函数的定义是:dp(s1, i, s2, j) 计算 s1[i..] 和 s2[j..] 的最长公共子序列长度。
根据这个定义,那么我们想要的答案就是 dp(s1, 0, s2, 0),且 base case 就是 i == len(s1) 或 j == len(s2) 时,因为这时候 s1[i..] 或 s2[j..] 就相当于空串了,最长公共子序列的长度显然是 0:
int longestCommonSubsequence(String s1, String s2) {
return dp(s1, 0, s2, 0);
}
/* 主函数 */
int dp(String s1, int i, String s2, int j) {
// base case
if (i == s1.length() || j == s2.length()) {
return 0;
}
// ...
接下来,咱不要看 s1 和 s2 两个字符串,而是要具体到每一个字符,思考每个字符该做什么。
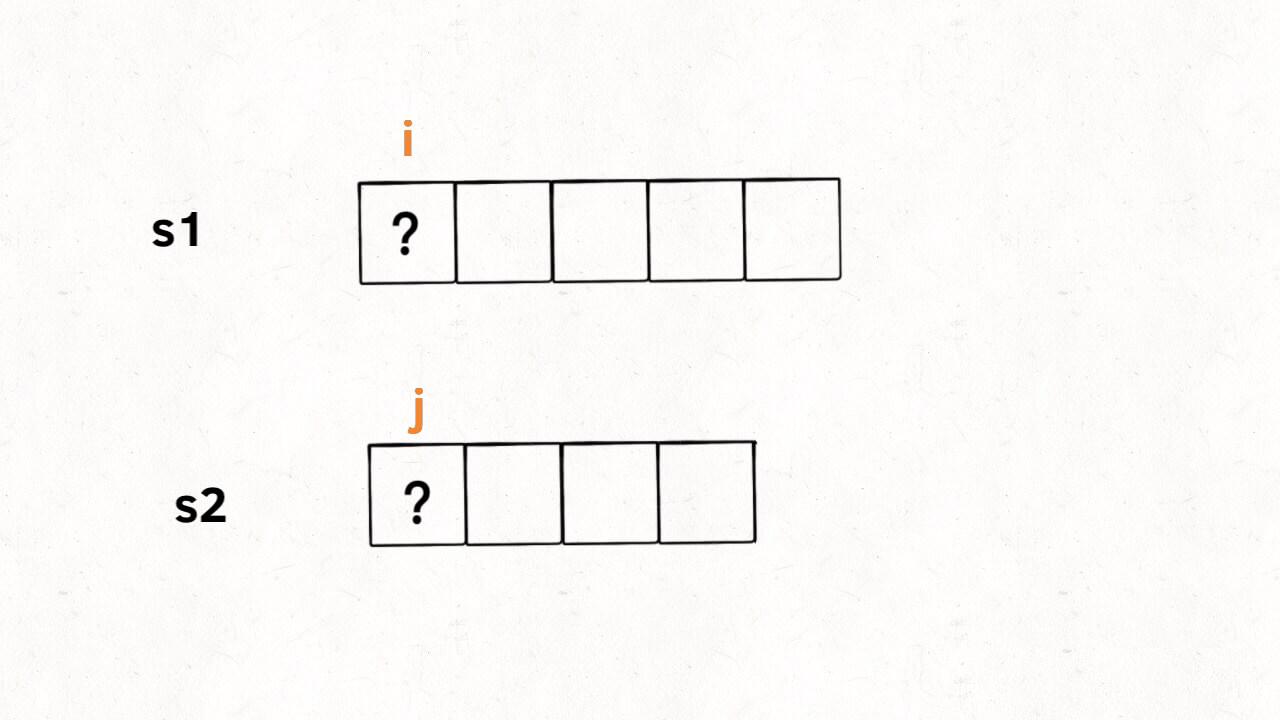
我们只看 s1[i] 和 s2[j],如果 s1[i] == s2[j],说明这个字符一定在 lcs 中:
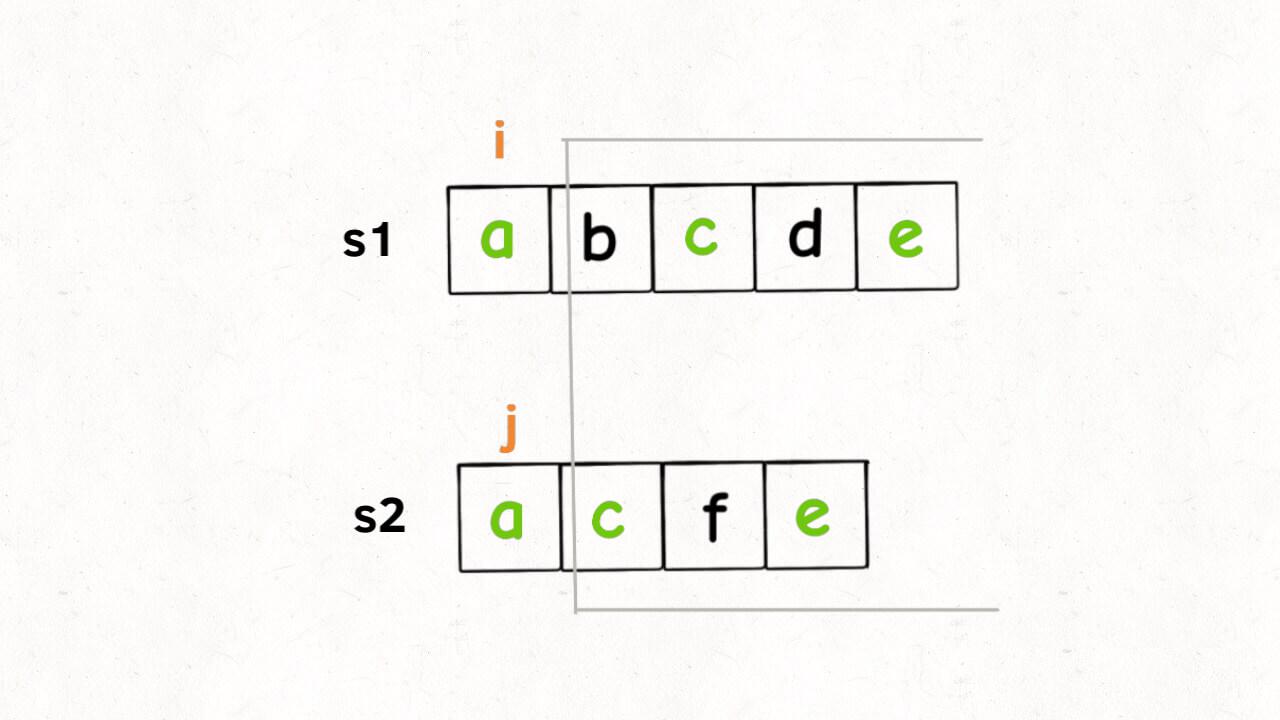
这样,就找到了一个 lcs 中的字符,根据 dp 函数的定义,我们可以完善一下代码:
// 定义:计算 s1[i..] 和 s2[j..] 的最长公共子序列长度
int dp(String s1, int i, String s2, int j) {
if (s1.charAt(i) == s2.charAt(j)) {
// s1[i] 和 s2[j] 必然在 lcs 中,
// 加上 s1[i+1..] 和 s2[j+1..] 中的 lcs 长度,就是答案
return 1 + dp(s1, i + 1, s2, j + 1)
} else {
// ...
}
}
刚才说的 s1[i] == s2[j] 的情况,但如果 s1[i] != s2[j],应该怎么办呢?
s1[i] != s2[j] 意味着,s1[i] 和 s2[j] 中至少有一个字符不在 lcs 中:
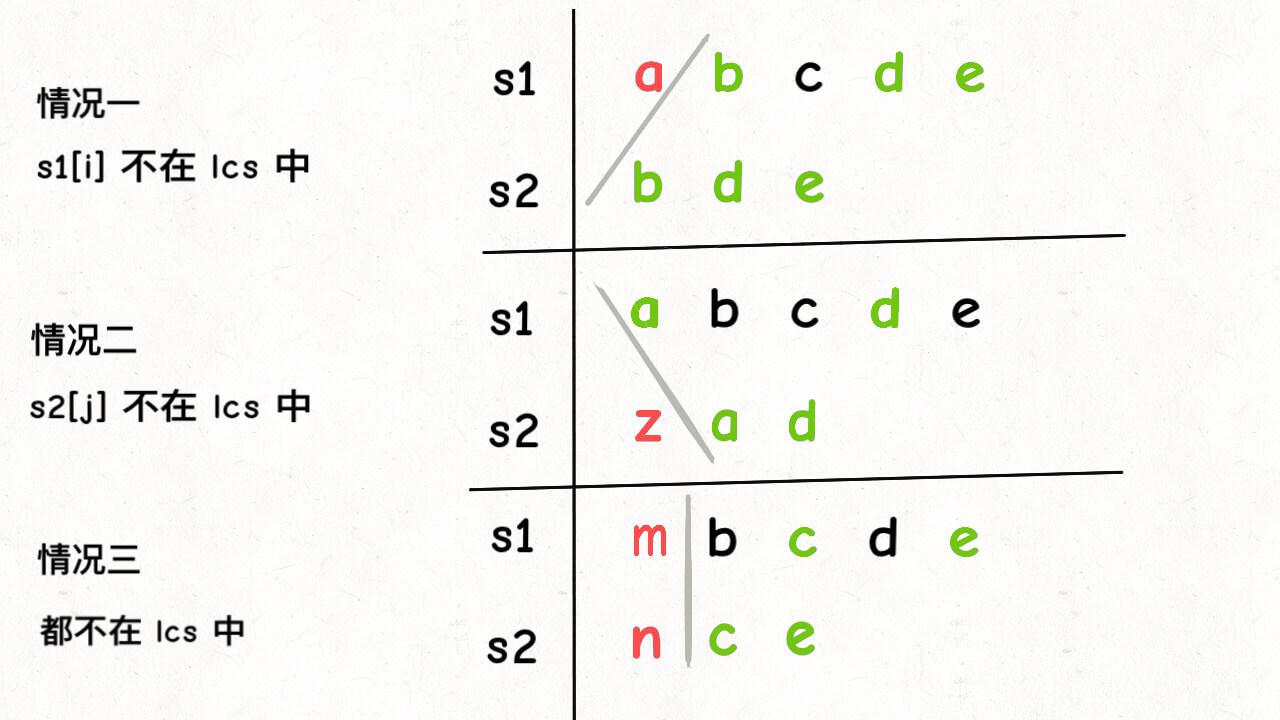
如上图,总共可能有三种情况,我怎么知道具体是那种情况呢?
其实我们也不知道,那就把这三种情况的答案都算出来,取其中结果最大的那个呗,因为题目让我们算「最长」公共子序列的长度嘛。
这三种情况的答案怎么算?回想一下我们的 dp 函数定义,不就是专门为了计算它们而设计的嘛!
代码可以再进一步:
// 定义:计算 s1[i..] 和 s2[j..] 的最长公共子序列长度
int dp(String s1, int i, String s2, int j) {
if (s1.charAt(i) == s2.charAt(j)) {
return 1 + dp(s1, i + 1, s2, j + 1)
} else {
// s1[i] 和 s2[j] 中至少有一个字符不在 lcs 中,
// 穷举三种情况的结果,取其中的最大结果
return max(
// 情况一、s1[i] 不在 lcs 中
dp(s1, i + 1, s2, j),
// 情况二、s2[j] 不在 lcs 中
dp(s1, i, s2, j + 1),
// 情况三、都不在 lcs 中
dp(s1, i + 1, s2, j + 1)
);
}
}
这里就已经非常接近我们的最终答案了,还有一个小的优化,情况三「s1[i] 和 s2[j] 都不在 lcs 中」其实可以直接忽略。
因为我们在求最大值嘛,情况三在计算 s1[i+1..] 和 s2[j+1..] 的 lcs 长度,这个长度肯定是小于等于情况二 s1[i..] 和 s2[j+1..] 中的 lcs 长度的,因为 s1[i+1..] 比 s1[i..] 短嘛,那从这里面算出的 lcs 当然也不可能更长嘛。
同理,情况三的结果肯定也小于等于情况一。说白了,情况三被情况一和情况二包含了,所以我们可以直接忽略掉情况三,完整代码如下:
// 备忘录,消除重叠子问题
int[][] memo;
/* 主函数 */
int longestCommonSubsequence(String s1, String s2) {
int m = s1.length(), n = s2.length();
// 备忘录值为 -1 代表未曾计算
memo = new int[m][n];
for (int[] row : memo)
Arrays.fill(row, -1);
// 计算 s1[0..] 和 s2[0..] 的 lcs 长度
return dp(s1, 0, s2, 0);
}
// 定义:计算 s1[i..] 和 s2[j..] 的最长公共子序列长度
int dp(String s1, int i, String s2, int j) {
// base case
if (i == s1.length() || j == s2.length()) {
return 0;
}
// 如果之前计算过,则直接返回备忘录中的答案
if (memo[i][j] != -1) {
return memo[i][j];
}
// 根据 s1[i] 和 s2[j] 的情况做选择
if (s1.charAt(i) == s2.charAt(j)) {
// s1[i] 和 s2[j] 必然在 lcs 中
memo[i][j] = 1 + dp(s1, i + 1, s2, j + 1);
} else {
// s1[i] 和 s2[j] 至少有一个不在 lcs 中
memo[i][j] = Math.max(
dp(s1, i + 1, s2, j),
dp(s1, i, s2, j + 1)
);
}
return memo[i][j];
}
以上思路完全就是按照我们之前的爆文动态规划套路框架来的,应该是很容易理解的。至于为什么要加 memo 备忘录,我们之前写过很多次,为了照顾新来的读者,这里再简单重复一下,首先抽象出我们核心 dp 函数的递归框架:
int dp(int i, int j) {
dp(i + 1, j + 1); // #1
dp(i, j + 1); // #2
dp(i + 1, j); // #3
}
你看,假设我想从 dp(i, j) 转移到 dp(i+1, j+1),有不止一种方式,可以直接走 #1,也可以走 #2 -> #3,也可以走 #3 -> #2。
这就是重叠子问题,如果我们不用 memo 备忘录消除子问题,那么 dp(i+1, j+1) 就会被多次计算,这是没有必要的。
至此,最长公共子序列问题就完全解决了,用的是自顶向下带备忘录的动态规划思路,我们当然也可以使用自底向上的迭代的动态规划思路,和我们的递归思路一样,关键是如何定义 dp 数组,我这里也写一下自底向上的解法吧:
int longestCommonSubsequence(String s1, String s2) {
int m = s1.length(), n = s2.length();
int[][] dp = new int[m + 1][n + 1];
// 定义:s1[0..i-1] 和 s2[0..j-1] 的 lcs 长度为 dp[i][j]
// 目标:s1[0..m-1] 和 s2[0..n-1] 的 lcs 长度,即 dp[m][n]
// base case: dp[0][..] = dp[..][0] = 0
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
// 现在 i 和 j 从 1 开始,所以要减一
if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
// s1[i-1] 和 s2[j-1] 必然在 lcs 中
dp[i][j] = 1 + dp[i - 1][j - 1];
} else {
// s1[i-1] 和 s2[j-1] 至少有一个不在 lcs 中
dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
}
}
}
return dp[m][n];
}
自底向上的解法中 dp 数组定义的方式和我们的递归解法有一点差异,而且由于数组索引从 0 开始,有索引偏移,不过思路和我们的递归解法完全相同,如果你看懂了递归解法,这个解法应该不难理解。
另外,自底向上的解法可以通过我们前文讲过的动态规划状态压缩技巧来进行优化,把空间复杂度压缩为 O(N),这里由于篇幅所限,就不展开了。
下面,来看两道和最长公共子序列相似的两道题目。
字符串的删除操作
这是力扣第 583 题「两个字符串的删除操作」,看下题目:

函数签名如下:
int minDistance(String s1, String s2);
题目让我们计算将两个字符串变得相同的最少删除次数,那我们可以思考一下,最后这两个字符串会被删成什么样子?
删除的结果不就是它俩的最长公共子序列嘛!
那么,要计算删除的次数,就可以通过最长公共子序列的长度推导出来:
int minDistance(String s1, String s2) {
int m = s1.length(), n = s2.length();
// 复用前文计算 lcs 长度的函数
int lcs = longestCommonSubsequence(s1, s2);
return m - lcs + n - lcs;
}
这道题就解决了!
最小 ASCII 删除和
这是力扣第 712 题,看下题目:

这道题,和上一道题非常类似,这回不问我们删除的字符个数了,问我们删除的字符的 ASCII 码加起来是多少。
那就不能直接复用计算最长公共子序列的函数了,但是可以依照之前的思路,稍微修改 base case 和状态转移部分即可直接写出解法代码:
// 备忘录
int memo[][];
/* 主函数 */
int minimumDeleteSum(String s1, String s2) {
int m = s1.length(), n = s2.length();
// 备忘录值为 -1 代表未曾计算
memo = new int[m][n];
for (int[] row : memo)
Arrays.fill(row, -1);
return dp(s1, 0, s2, 0);
}
// 定义:将 s1[i..] 和 s2[j..] 删除成相同字符串,
// 最小的 ASCII 码之和为 dp(s1, i, s2, j)。
int dp(String s1, int i, String s2, int j) {
int res = 0;
// base case
if (i == s1.length()) {
// 如果 s1 到头了,那么 s2 剩下的都得删除
for (; j < s2.length(); j++)
res += s2.charAt(j);
return res;
}
if (j == s2.length()) {
// 如果 s2 到头了,那么 s1 剩下的都得删除
for (; i < s1.length(); i++)
res += s1.charAt(i);
return res;
}
if (memo[i][j] != -1) {
return memo[i][j];
}
if (s1.charAt(i) == s2.charAt(j)) {
// s1[i] 和 s2[j] 都是在 lcs 中的,不用删除
memo[i][j] = dp(s1, i + 1, s2, j + 1);
} else {
// s1[i] 和 s2[j] 至少有一个不在 lcs 中,删一个
memo[i][j] = Math.min(
s1.charAt(i) + dp(s1, i + 1, s2, j),
s2.charAt(j) + dp(s1, i, s2, j + 1)
);
}
return memo[i][j];
}
base case 有一定区别,计算 lcs 长度时,如果一个字符串为空,那么 lcs 长度必然是 0;但是这道题如果一个字符串为空,另一个字符串必然要被全部删除,所以需要计算另一个字符串所有字符的 ASCII 码之和。
关于状态转移,当 s1[i] 和 s2[j] 相同时不需要删除,不同时需要删除,所以可以利用 dp 函数计算两种情况,得出最优的结果。其他的大同小异,就不具体展开了。
至此,三道子序列问题就解决完了,关键在于将问题细化到字符,根据每两个字符是否相同来判断他们是否在结果子序列中,从而避免了对所有子序列进行穷举。
这也算是在两个字符串中求子序列的常用思路吧,建议好好体会,多多练习~