Binary Search Algorithm Code Template
This article will resolve
| LeetCode | Difficulty |
|---|---|
| 34. Find First and Last Position of Element in Sorted Array | 🟠 |
| 704. Binary Search | 🟢 |
This article is a revised version of the old article Detailed Binary Search, with more detailed analysis of the binary search algorithm.
Let me start with a joke:
One day, A-Dong borrowed N books from the library. When leaving, the alarm went off. The security guard stopped A-Dong to check which book was not properly checked out. A-Dong was about to scan each book under the detector to find the problem book, but the security guard rolled his eyes: "You don't know binary search?"
The guard divided the books into two piles and scanned the first pile. The alarm went off, so the problem book was in that pile. He split the pile again, scanned the first half, the alarm went off again, and so on...
After about logN scans, the guard found the problem book and looked smug. A-Dong left with the other books.
Since then, the library lost N - 1 books.
Binary search is not easy. Even Knuth (the creator of the KMP algorithm) once said: The concept is simple, but the details are tricky. Many people talk about integer overflow bugs, but the real difficulties with binary search aren't just about that. It's about whether you should add or subtract one from mid, and whether the while loop should use <= or <.
If you don't understand these details, writing binary search is just guesswork. If there are bugs, you can only hope you get lucky.
This article explores the most common binary search situations: finding a number, finding the left boundary, and finding the right boundary. We will dive deep into details, such as whether inequalities should include the equal sign, and whether mid should be adjusted up or down. We will look at why these differences exist so you can flexibly and accurately write correct binary search algorithms.
One more note: For every scenario, I will show different code styles. This is so you understand why these small differences exist. At least, you won't be confused by others' code. There is no "best" style—use the one you like.
0. Binary Search Template
int binarySearch(int[] nums, int target) {
int left = 0, right = ...;
while(...) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
...
} else if (nums[mid] < target) {
left = ...
} else if (nums[mid] > target) {
right = ...
}
}
return ...;
}int binarySearch(vector<int>& nums, int target) {
int left = 0, right = nums.size() - 1;
while (...) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
...
} else if (nums[mid] < target) {
left = ...
} else if (nums[mid] > target) {
right = ...
}
}
}def binarySearch(nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1
while ...:
mid = left + (right - left) // 2
if nums[mid] == target:
...
elif nums[mid] < target:
left = ...
elif nums[mid] > target:
right = ...
return ...func binarySearch(nums []int, target int) int {
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right-left)/2
if nums[mid] == target {
...
} else if nums[mid] < target {
left = ...
} else if nums[mid] > target {
right = ...
}
}
return ...
}var binarySearch = function(nums, target) {
var left = 0, right = nums.length - 1;
while (...) {
var mid = left + Math.floor((right - left) / 2);
if (nums[mid] == target) {
...
} else if (nums[mid] < target) {
left = ...
} else if (nums[mid] > target) {
right = ...
}
}
return ...;
}A good tip when writing binary search: Don't use else. Instead, use else if to show every possible case clearly. In this article, I will use else if to make all the details clear. Once you understand, you can simplify the code yourself.
The parts marked with ... are the places where tricky details can hide. When you see binary search code, always pay special attention to these spots. Later, we will use examples to talk about how these can change.
By the way, to avoid overflow when calculating mid, use left + (right - left) / 2 instead of (left + right) / 2. This prevents overflow when left and right are big numbers.
1. Finding a Number (Basic Binary Search)
This is the simplest and most common situation: search for a number in a sorted array. If found, return its index. Otherwise, return -1.
class Solution {
// standard binary search framework, search for the index of
// the target element, return -1 if it does not exist
public int search(int[] nums, int target) {
int left = 0;
// note
int right = nums.length - 1;
while(left <= right) {
int mid = left + (right - left) / 2;
if(nums[mid] == target) {
return mid;
} else if (nums[mid] < target) {
// note
left = mid + 1;
} else if (nums[mid] > target) {
// note
right = mid - 1;
}
}
return -1;
}
}class Solution {
public:
// standard binary search framework, search for the index of
// the target element, return -1 if it does not exist
int search(vector<int>& nums, int target) {
int left = 0;
// note
int right = nums.size() - 1;
while(left <= right) {
int mid = left + (right - left) / 2;
if(nums[mid] == target) {
return mid;
} else if (nums[mid] < target) {
// note
left = mid + 1;
} else if (nums[mid] > target) {
// note
right = mid - 1;
}
}
return -1;
}
};class Solution:
# standard binary search framework, search for the index
# of the target element, return -1 if it does not exist
def search(self, nums: List[int], target: int) -> int:
left = 0
# note
right = len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] == target:
return mid
elif nums[mid] < target:
# note
left = mid + 1
elif nums[mid] > target:
# note
right = mid - 1
return -1// standard binary search framework, search for the index
// of the target element, return -1 if it does not exist
func search(nums []int, target int) int {
left := 0
// note
right := len(nums) - 1
for left <= right {
mid := left + (right-left)/2
if nums[mid] == target {
return mid
} else if nums[mid] < target {
// note
left = mid + 1
} else if nums[mid] > target {
// note
right = mid - 1
}
}
return -1
}var search = function(nums, target) {
// standard binary search framework, search for the index of
// the target element, return -1 if it does not exist
let left = 0;
// note
let right = nums.length - 1;
while (left <= right) {
let mid = left + Math.floor((right - left) / 2);
if (nums[mid] === target) {
return mid;
} else if (nums[mid] < target) {
// note
left = mid + 1;
} else if (nums[mid] > target) {
// note
right = mid - 1;
}
}
return -1;
};Algorithm Visualization
This code works for LeetCode problem 704: Binary Search. But let's look closer at the details.
Why is the while loop condition <= and not <?
Answer: Because right is set to nums.length - 1 at the start, which is the last index—not nums.length.
In some versions of binary search, you might see right = nums.length. The difference is:
right = nums.length - 1means the search interval is closed on both sides:[left, right].right = nums.lengthmeans the search interval is[left, right): left-closed, right-open.
Since an index of nums.length is out of bounds, we treat the right side as an open interval in that case.
This code uses [left, right], closed on both sides. This is the current search interval.
When should searching stop? Of course, when we find the target:
if (nums[mid] == target)
return mid;But if we don't find it, we need the while loop to end and return -1. So, when does the while loop end? When the search interval is empty. That means there is nothing left to look for.
while (left <= right) ends when left == right + 1. The interval becomes [right + 1, right], for example [3, 2]. This interval is empty, since no number can satisfy both conditions. So, ending the loop here and returning -1 is correct.
With while (left < right), the loop ends when left == right. The interval is [right, right], for example [2, 2]. This interval is not empty (it still holds the number at index 2). If we just return -1 now, we might be skipping the last possible check, and that could be a mistake.
Of course, you can use while (left < right) if you fix this:
// ...
while (left < right) {
// ...
}
return nums[left] == target ? left : -1;Why do we do left = mid + 1 and right = mid - 1?
Some code uses right = mid or left = mid, without the +1 or -1. How do you decide which is correct?
Answer: It's all about the search interval.
We said before that our search interval is [left, right] (closed on both sides). So, when mid is not the target, what next?
We should search either [left, mid - 1] or [mid + 1, right]. Because we already know mid is not the answer—it's already checked and should be excluded.
What is the limitation of this algorithm?
Now you know all the details for this case, and why things are done this way. But this algorithm has some limits.
For example, given the sorted array nums = [1,2,2,2,3], and target = 2, this code returns index 2. That's fine. But what if you want the leftmost index (1) or rightmost index (3) of the target? This code does not handle those.
This need comes up often. You might say, "Just scan to the left or right after finding the target." Sure, but then you're back to brute-force and lose the log(N) efficiency.
In the next section, we will talk about finding the left and right boundaries with binary search.
2. Binary Search for the Left Boundary
Here is the most common code pattern. Pay attention to the details marked below:
int left_bound(int[] nums, int target) {
int left = 0;
// note
int right = nums.length;
// note
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
right = mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
// note
right = mid;
}
}
return left;
}int left_bound(vector<int>& nums, int target) {
int left = 0;
// note
int right = nums.size();
// note
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
right = mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
// note
right = mid;
}
}
return left;
}def left_bound(nums: List[int], target: int) -> int:
left = 0
# note
right = len(nums)
# note
while left < right:
mid = left + (right - left) // 2
if nums[mid] == target:
right = mid
elif nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
# note
right = mid
return leftfunc left_bound(nums []int, target int) int {
left := 0
// note
right := len(nums)
// note
for left < right {
mid := left + (right - left) / 2
if nums[mid] == target {
right = mid
} else if nums[mid] < target {
left = mid + 1
} else if nums[mid] > target {
// note
right = mid
}
}
return left
}var left_bound = function(nums, target) {
var left = 0;
// note
var right = nums.length;
// note
while (left < right) {
var mid = left + Math.floor((right - left) / 2);
if (nums[mid] == target) {
right = mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
// note
right = mid;
}
}
return left;
}Why is the while condition < and not <=?
Because we set right = nums.length instead of nums.length - 1, the search range each loop is [left, right), which is left-closed, right-open.
The loop while(left < right) ends when left == right. At this point, the search range [left, left) is empty, so the loop stops correctly.
Info
Many people ask: Isn't right usually nums.length - 1? Why here do we use nums.length and make the search range left-closed, right-open?
The reason is, for searching the left or right boundaries, this way of writing is common. I use this approach as an example to make sure you can understand code you see later. If you prefer, you can use the version where both sides are closed, which is even simpler. Later, I will unify all three binary search patterns using the closed interval version, so keep reading.
What if target does not exist? What does the function return?
If target is not in nums, what does the returned index mean? What if you want it to return -1?
What does left_bound return if target does not exist?
This is a good and important question. Once you understand this, you will not get confused when applying binary search in real problems.
Here's the answer: If target does not exist, the binary search for the left boundary returns the smallest index where the element is greater than target.
Example: nums = [2,3,5,7], target = 4, the left_bound function returns 2, because the element 5 is the smallest element greater than 4.
This might sound a bit confusing. The left_bound function is for finding the left boundary, but if target does not exist, it returns the index of the smallest element greater than target. Don't memorize this conclusion; just try a simple example if you are not sure.
Binary search is simple in idea, but the details are tricky, and there are many pitfalls. If you want to be strong at this, you need to understand these details well. If you use code templates without knowing these details, you might face weird bugs and not know how to fix them.
Actually, this left_bound behavior has a good use. For example, if you need to write a floor function, you can use left_bound like this:
// In a sorted array, find the index of the largest element less than target.
// Example: nums = [1,2,2,2,3], target = 2, function returns 0 because 1 is the largest element less than 2.
// Example: nums = [1,2,3,5,6], target = 4, function returns 2 because 3 is the largest element less than 4.
int floor(int[] nums, int target) {
// If target does not exist, e.g. [4,6,8,10], target = 7:
// left_bound returns 2, minus one is 1, element 6 is the largest less than 7.
// If target exists, e.g. [4,6,8,8,8,10], target = 8:
// left_bound returns 2, minus one is 1, element 6 is the largest less than 8.
return left_bound(nums, target) - 1;
}My suggestion: if you must write binary search by hand, you need to understand all these details. This article helps you sort them out. If possible, use the standard library functions provided by your language. They are well documented and less likely to cause bugs.
If you want the function to return -1 when target does not exist, that's easy. Just add a check before you return: check if nums[left] == target. If not, return -1. You must also make sure left is not out of bounds:
while (left < right) {
// ...
}
// If index is out of bounds, target is not in array, return -1
if (left < 0 || left >= nums.length) {
return -1;
}
// Tip: Actually, "left < 0" is never true here, because left starts from 0 and only moves right,
// but it is a good habit to check both ends, especially for unified templates or when searching right boundary.
return nums[left] == target ? left : -1;Why do we use left = mid + 1 and right = mid?
Because our search range is [left, right), left-closed, right-open. So after checking nums[mid], we should next search either [left, mid) or [mid + 1, right).
Why does this algorithm find the left boundary?
The key is how we handle nums[mid] == target:
if (nums[mid] == target)
right = mid;When we find target, we do not return immediately. Instead, we move the upper boundary right to mid and keep searching in [left, mid). We keep shrinking the search area to the left, locking in the left boundary.
Why return left instead of right?
They are the same, because the loop ends with left == right.
Can we use a search range that is closed on both ends?
Can we set right to be nums.length - 1, making both ends of the search interval closed? This would make it more similar to the first type of binary search.
Answer: Yes, you can. As long as you understand the idea of "search interval," you won't miss any element, and you can adjust the code as you like. Let's change it according to the logic:
Since you want to use a closed interval on both ends, set right to nums.length - 1, and the while loop condition should be left <= right:
int left_bound(int[] nums, int target) {
// Search range is [left, right]
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
// if else ...
}
}Because both ends are included, and we are searching for the left boundary, update left and right like this:
if (nums[mid] < target) {
// Search range becomes [mid+1, right]
left = mid + 1;
} else if (nums[mid] > target) {
// Search range becomes [left, mid-1]
right = mid - 1;
} else if (nums[mid] == target) {
// Narrow the right boundary
right = mid - 1;
}If you want to return -1 when the target is not found, just check if nums[left] equals target:
// If target is larger than all numbers, return -1
if (left == nums.length) return -1;
// Check if nums[left] is target
return nums[left] == target ? left : -1;Now the algorithm is done. Here is the full code:
int left_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
// the search range is [left, right]
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
// the search range becomes [mid+1, right]
left = mid + 1;
} else if (nums[mid] > target) {
// the search range becomes [left, mid-1]
right = mid - 1;
} else if (nums[mid] == target) {
// shrink the right boundary
right = mid - 1;
}
}
// determine if target exists in nums
// if out of bounds, target definitely does not exist, return -1
if (left < 0 || left >= nums.length) {
return -1;
}
// check if nums[left] is the target
return nums[left] == target ? left : -1;
}int left_bound(vector<int>& nums, int target) {
int left = 0, right = nums.size() - 1;
// the search range is [left, right]
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
// the search range becomes [mid+1, right]
left = mid + 1;
} else if (nums[mid] > target) {
// the search range becomes [left, mid-1]
right = mid - 1;
} else if (nums[mid] == target) {
// shrink the right boundary
right = mid - 1;
}
}
// determine if target exists in nums
// if out of bounds, target definitely does not exist, return -1
if (left < 0 || left >= nums.size()) {
return -1;
}
// check if nums[left] is target
return nums[left] == target ? left : -1;
}def left_bound(nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1
# the search range is [left, right]
while left <= right:
mid = left + (right - left) // 2
if nums[mid] < target:
# the search range becomes [mid+1, right]
left = mid + 1
elif nums[mid] > target:
# the search range becomes [left, mid-1]
right = mid - 1
elif nums[mid] == target:
# shrink the right boundary
right = mid - 1
# determine if target exists in nums
# if out of bounds, target definitely does not exist, return -1
if left < 0 or left >= len(nums):
return -1
# determine if nums[left] is target
return left if nums[left] == target else -1// Search for the left boundary of the target in the given nums
func left_bound(nums []int, target int) int {
left := 0
right := len(nums) - 1
// the search range is [left, right]
for left <= right {
mid := left + (right - left) / 2
if nums[mid] < target {
// the search range becomes [mid+1, right]
left = mid + 1
} else if nums[mid] > target {
// the search range becomes [left, mid-1]
right = mid - 1
} else if nums[mid] == target {
// shrink the right boundary
right = mid - 1
}
}
// determine if the target exists in nums
if left < 0 || left >= len(nums) {
return -1
}
// if out of bounds, the target definitely does not exist, return -1
if nums[left] == target {
// determine if nums[left] is the target
return left
}
return -1
}var left_bound = function(nums, target) {
var left = 0, right = nums.length - 1;
// the search range is [left, right]
while (left <= right) {
var mid = left + Math.floor((right - left) / 2);
if (nums[mid] < target) {
// the search range becomes [mid+1, right]
left = mid + 1;
} else if (nums[mid] > target) {
// the search range becomes [left, mid-1]
right = mid - 1;
} else if (nums[mid] == target) {
// shrink the right boundary
right = mid - 1;
}
}
// determine if target exists in nums
// if out of bounds, target definitely does not exist, return -1
if (left < 0 || left >= nums.length) {
return -1;
}
// check if nums[left] is target
return nums[left] == target ? left : -1;
};Algorithm Visualization
Now, this is the same as the first type of binary search. Both use fully closed search intervals, and the final result is also the value of left. As long as you follow the logic, you can remember whichever style you prefer.
3. Finding the Right Boundary in Binary Search
This is similar to finding the left boundary. Here are two methods. Let’s start with the common left-closed, right-open style. Compared to searching for the left boundary, there are two changes:
int right_bound(int[] nums, int target) {
int left = 0, right = nums.length;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
// Important!
left = mid + 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
// Important!
return left - 1;
}Why does this code find the right boundary?
Answer: The key point is here:
if (nums[mid] == target) {
left = mid + 1;
}When nums[mid] == target, do not return immediately. Instead, increase the left boundary (left). This makes the search interval move right, helping us lock in the right boundary.
Why return left - 1?
Why do we return left - 1 instead of left (as in the left boundary search)? Shouldn't we return right when searching for the right boundary?
Answer: The while loop ends when left == right, so left and right are equal at that point. To show we are searching the right side, you can return right - 1.
As for why we need to subtract one, it's because of how we update left:
// Increase left to lock right boundary
if (nums[mid] == target) {
left = mid + 1;
// Think about it like: mid = left - 1
}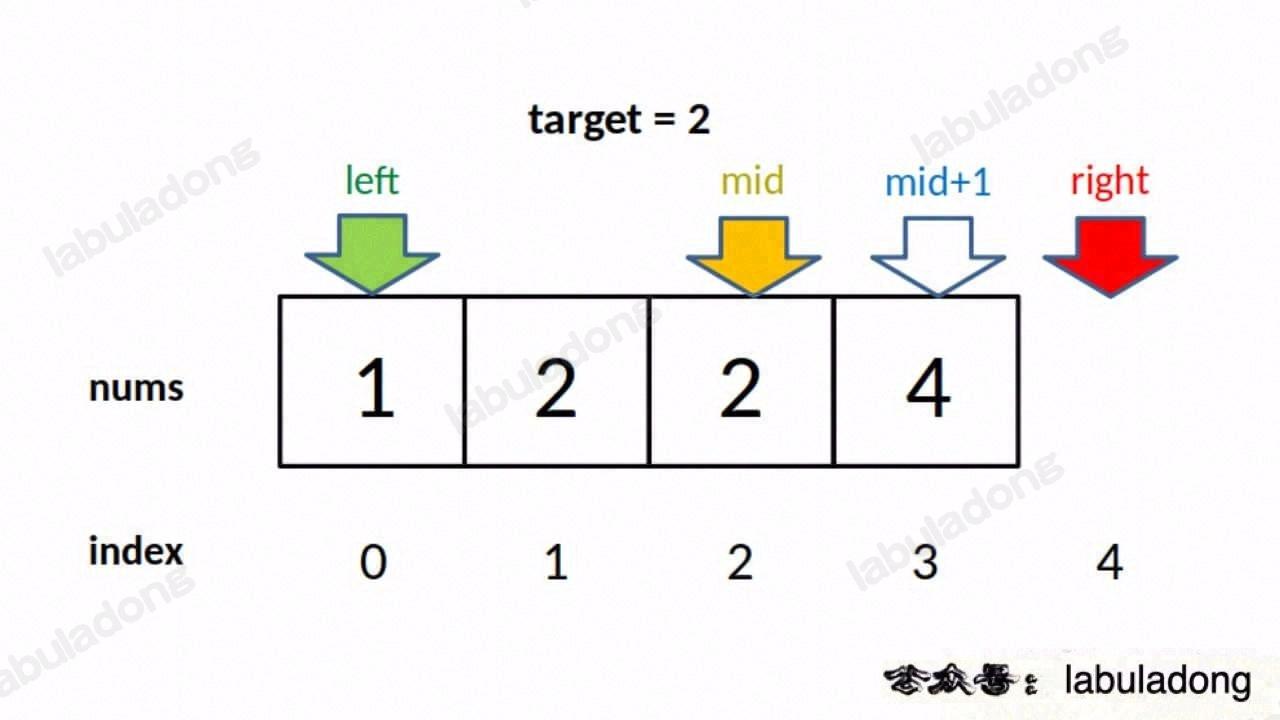
Because we always set left = mid + 1, at the end of the loop, nums[left] is not equal to target anymore, but nums[left - 1] might be the target.
The reason we must use left = mid + 1 is to make sure that nums[mid] is excluded from the search interval. We won't go over this in detail here.
What to return if target does not exist?
If target is not in nums, what does the returned index mean? What if I want it to return -1?
What does right_bound return when target is not found
Here is the answer. Opposite to the left_bound: If target does not exist, the binary search for the right boundary returns the largest index whose value is less than target.
You don't need to memorize this. You can figure it out with an example. For example, nums = [2,3,5,7], target = 4, the right_bound function returns 1, because 3 is the largest element less than 4.
Just like before, since binary search code can be tricky, if not necessary, try to use the standard library functions that your programming language provides.
If you want to return -1 when target does not exist, it is simple. In the end, you just need to check if nums[left-1] is target, similar to the left boundary search, just add an extra check:
while (left < right) {
// ...
}
// Check if target exists in nums
// If left - 1 is out of bounds, target is not in nums
if (left - 1 < 0 || left - 1 >= nums.length) {
return -1;
}
// Check if nums[left - 1] is target
return nums[left - 1] == target ? (left - 1) : -1;4. Can we also use a "both closed" search range for this algorithm? Then all three versions of binary search will be the same, and you can write them easily next time.
Yes, you can. Similar to searching for the left boundary, you just need to change two things in the code:
int right_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// here change to shrink the left boundary
left = mid + 1;
}
}
// finally change to return left - 1
if (left - 1 < 0 || left - 1 >= nums.length) {
return -1;
}
return nums[left - 1] == target ? (left - 1) : -1;
}int right_bound(vector<int>& nums, int target) {
int left = 0, right = nums.size() - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// here, change it to shrink the left boundary
left = mid + 1;
}
}
// finally, change it to return left - 1
if (left - 1 < 0 || left - 1 >= nums.size()) {
return -1;
}
return nums[left - 1] == target ? (left - 1) : -1;
}def right_bound(nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
right = mid - 1
elif nums[mid] == target:
# here, change it to shrink the left boundary
left = mid + 1
# finally, change it to return left - 1
if left - 1 < 0 or left - 1 >= len(nums):
return -1
return left - 1 if nums[left - 1] == target else -1func rightBound(nums []int, target int) int {
left, right := 0, len(nums) - 1
for left <= right {
mid := left + (right - left) / 2
if nums[mid] < target {
left = mid + 1
} else if nums[mid] > target {
right = mid - 1
} else if nums[mid] == target {
// here, just shrink the left boundary
left = mid + 1
}
}
// finally, return left - 1
if left - 1 < 0 || left - 1 >= len(nums) {
return -1
}
if nums[left - 1] == target {
return left - 1
}
return -1
}var right_bound = function(nums, target) {
var left = 0, right = nums.length - 1;
while (left <= right) {
var mid = left + Math.floor((right - left) / 2);
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// change here to shrink the left boundary
left = mid + 1;
}
}
// finally, change to return left - 1
if (left - 1 < 0 || left - 1 >= nums.length) {
return -1;
}
return nums[left - 1] == target ? (left - 1) : -1;
};Algorithm Visualization
Also, since the while loop ends with right == left - 1, you can just change all the left - 1 above to right. This makes it a bit clearer that you are searching for the right boundary:
int right_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// Move the left boundary to the right
left = mid + 1;
}
}
// Now return right
if (right < 0 || right >= nums.length) {
return -1;
}
return nums[right] == target ? right : -1;
}Now you have two ways to write the binary search for the right boundary. In fact, unifying the search range as "both closed" is easier to remember, right?
4. Unified Logic
With binary search for finding left and right boundaries, you can solve LeetCode 34: Find First and Last Position of Element in Sorted Array. Let’s go through the logic behind the small differences in these binary search methods:
First, the most basic binary search:
Because we initialize right = nums.length - 1
This means the search range is [left, right]
So we use while (left <= right)
And we update left = mid + 1 and right = mid - 1
Since we only need to find one target index,
When nums[mid] == target, we can return immediatelySecond, binary search for the left boundary:
Because we initialize right = nums.length
This means the search range is [left, right)
So we use while (left < right)
And we update left = mid + 1 and right = mid
Since we need to find the leftmost index,
When nums[mid] == target, do not return immediately
We should tighten the right boundary to lock the leftmost indexThird, binary search for the right boundary:
Because we initialize right = nums.length
This means the search range is [left, right)
So we use while (left < right)
And we update left = mid + 1 and right = mid
Since we need to find the rightmost index,
When nums[mid] == target, do not return immediately
We should tighten the left boundary to lock the rightmost index
Also, since we always move left = mid + 1 when locking the left boundary,
In the end, we must subtract one from left or right as the resultTo find left or right boundaries, a common method is to use a left-closed, right-open [left, right) search range. If you want to remember them easily, you can turn all search ranges into both ends closed [left, right]. Only change two places in your code to get all three search versions.
int binary_search(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while(left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if(nums[mid] == target) {
// return directly
return mid;
}
}
// return directly
return -1;
}
int left_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// do not return, lock the left boundary
right = mid - 1;
}
}
// determine if target exists in nums
if (left < 0 || left >= nums.length) {
return -1;
}
// check if nums[left] is the target
return nums[left] == target ? left : -1;
}
int right_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// do not return, lock the right boundary
left = mid + 1;
}
}
// since the while loop ends with right == left - 1
// and we are now looking for the right boundary
// it's easier to remember to use right instead of left - 1
if (right < 0 || right >= nums.length) {
return -1;
}
return nums[right] == target ? right : -1;
}int binary_search(vector<int>& nums, int target) {
int left = 0, right = nums.size()-1;
while(left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if(nums[mid] == target) {
// return directly
return mid;
}
}
// return directly
return -1;
}
int left_bound(vector<int>& nums, int target) {
int left = 0, right = nums.size()-1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// do not return, lock the left boundary
right = mid - 1;
}
}
// determine if target exists in nums
if (left < 0 || left >= nums.size()) {
return -1;
}
// check if nums[left] is target
return nums[left] == target ? left : -1;
}
int right_bound(vector<int>& nums, int target) {
int left = 0, right = nums.size()-1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// do not return, lock the right boundary
left = mid + 1;
}
}
// since the while loop ends when right == left -
// 1, and we are now finding the right boundary
// so it's easier to remember to use right instead of left - 1
if (right < 0 || right >= nums.size()) {
return -1;
}
return nums[right] == target ? right : -1;
}def binary_search(nums: List[int], target: int) -> int:
# set left and right indexes
left, right = 0, len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
right = mid - 1
elif nums[mid] == target:
# found the target value
return mid
# target value not found
return -1
def left_bound(nums: List[int], target: int) -> int:
# set left and right indexes
left, right = 0, len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
right = mid - 1
elif nums[mid] == target:
# target exists, narrow the right boundary
right = mid - 1
# determine if the target exists
if left < 0 or left >= len(nums):
return -1
# determine if the left boundary found is the target value
return left if nums[left] == target else -1
def right_bound(nums: List[int], target: int) -> int:
# set left and right indexes
left, right = 0, len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
right = mid - 1
elif nums[mid] == target:
# target exists, narrow the left boundary
left = mid + 1
# determine if the target exists
if right < 0 or right >= len(nums):
return -1
# determine if the right boundary found is the target value
return right if nums[right] == target else -1func binarySearch(nums []int, target int) int {
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right - left) / 2
if nums[mid] < target {
left = mid + 1
} else if nums[mid] > target {
right = mid - 1
} else if nums[mid] == target {
// return directly
return mid
}
}
// return directly
return -1
}
func leftBound(nums []int, target int) int {
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right - left) / 2
if nums[mid] < target {
left = mid + 1
} else if nums[mid] > target {
right = mid - 1
} else if nums[mid] == target {
// do not return, lock the left boundary
right = mid - 1
}
}
// determine if target exists in nums
if left < 0 || left >= len(nums) {
return -1
}
// determine if nums[left] is target
if nums[left] == target {
return left
}
return -1
}
func rightBound(nums []int, target int) int {
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right - left) / 2
if nums[mid] < target {
left = mid + 1
} else if nums[mid] > target {
right = mid - 1
} else if nums[mid] == target {
// do not return, lock the right boundary
left = mid + 1
}
}
if right < 0 || right >= len(nums) {
return -1
}
if nums[right] == target {
return right
}
return -1
}var binary_search = function(nums, target) {
var left = 0, right = nums.length - 1;
while(left <= right) {
var mid = left + Math.floor((right - left) / 2);
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if(nums[mid] == target) {
// return directly
return mid;
}
}
// return directly
return -1;
}
var left_bound = function(nums, target) {
var left = 0, right = nums.length - 1;
while (left <= right) {
var mid = left + Math.floor((right - left) / 2);
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// do not return, lock the left boundary
right = mid - 1;
}
}
// determine if target exists in nums
if (left < 0 || left >= nums.length) {
return -1;
}
// check if nums[left] is the target
return nums[left] == target ? left : -1;
}
var right_bound = function(nums, target) {
var left = 0, right = nums.length - 1;
while (left <= right) {
var mid = left + Math.floor((right - left) / 2);
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// do not return, lock the right boundary
left = mid + 1;
}
}
// since the loop ends when right == left - 1 and we are looking for the right boundary
// so using right instead of left - 1 is easier to remember
if (right < 0 || right >= nums.length) {
return -1;
}
return nums[right] == target ? right : -1;
}If you understand the above, congratulations, these are all the details for binary search algorithms. Through this article, you have learned:
When writing binary search code, try not to use plain else. Write all logic as else if for better understanding. Once you write the correct logic, you can then merge branches to improve efficiency.
Pay attention to the search range and the stopping condition of the while loop. If there might be elements left out, remember to check at the end.
If you use a left-closed, right-open
[left, right)search range to find boundaries, just make some changes in the code whennums[mid] == target. When searching for the right boundary, you need to subtract one at the end.If you always use a left-closed, right-closed
[left, right]search range, it's easier to remember. Only slightly change the code where you check fornums[mid] == targetand how you return your answer. It is recommended to note this down as your binary search template.
Finally, I want to say, the frameworks above are techniques. If we look at the idea behind it, the key point of binary search is to use known information to reduce (cut in half) the search range as much as possible, so you can search faster and avoid brute-force searching.
If you understand this article, you can write correct binary search code. However, for real problems, you are not likely to be asked to write plain binary search code. I will explain more about applying binary search in Binary Search In Real World and More Binary Search Exercises.