Backtracking Algorithm Common Patterns and Code Template

This article is an advanced version of a long-ago Detailed Explanation of Backtracking Algorithm. Once you understand the framework, you'll realize that backtracking algorithm problems follow a common pattern.

This article addresses several questions:

What is the backtracking algorithm? What are the techniques for solving problems related to it? How can you learn the backtracking algorithm? Is there a pattern to writing backtracking algorithm code?

In fact, the backtracking algorithm can essentially be considered the same as what we commonly refer to as the DFS algorithm. Their subtle differences are explained in detail in Several Issues About DFS and Backtracking Algorithm. This article focuses on backtracking without delving into those differences.

Abstractly speaking, solving a backtracking problem is essentially a process of traversing a decision tree, where each leaf node of the tree contains a valid solution. By traversing the entire tree and collecting the solutions at the leaf nodes, you can obtain all valid solutions.

When standing at a node on the backtracking tree, you only need to consider three questions:

1. Path: the choices you have already made.
2. Choice List: the choices you can currently make.
3. End Condition: the condition under which you reach the bottom level of the decision tree and can no longer make choices.

If you don't understand these terms yet, that's okay. We will use the classic backtracking problem "permutations" later to help you understand what these terms mean. For now, just keep them in mind.

In terms of code, the framework for the backtracking algorithm is:

result = []
def backtrack(path, choice_list):
    if end_condition_met:
        result.add(path)
        return
    
    for choice in choice_list:
        make_choice
        backtrack(path, choice_list)
        undo_choice

The core concept is recursion within a for loop, making a choice before the recursive call and undoing the choice after the call. It is quite simple.

What does making and undoing a choice mean, and what is the fundamental principle of this framework? Let's resolve these questions through the "permutation" problem and explore the mysteries within it in detail!

Analysis of the Permutation Problem

LeetCode Problem 46 "Permutations" requires you to input an array nums and return all possible permutations of the numbers.

In high school, we solved mathematical problems of permutations and combinations. We know that for n distinct numbers, there are n! permutations in total. How did we enumerate all permutations back then?

For instance, given three numbers [1,2,3], you wouldn't enumerate them randomly without pattern. Generally, you would proceed like this:

First, fix the first position as 1, then the second position can be 2, leaving 3 for the third position. Then, change the second position to 3, leaving 2 for the third position. Next, change the first position to 2, and enumerate the last two positions...

This is essentially the backtracking algorithm. We naturally used it in high school without being taught, or some might have drawn a backtracking tree like this:

By traversing this tree from the root and recording the numbers on the path, you obtain all permutations. We might as well call this tree the "decision tree" of the backtracking algorithm.

Why call it a decision tree? Because at each node, you are making decisions. For example, standing at the red node below:

You are making a decision, choosing between the branch with 1 or the branch with 3. Why only between 1 and 3? Because the branch with 2 is behind you, a choice already made, and permutations do not allow repeated numbers.

Now we can clarify the initial terms: [2] is the "path," recording the choices you've made; [1,3] is the "choice list," representing the choices you can currently make; the "end condition" is reaching the leaf nodes at the tree's bottom layer, where the choice list is empty.

If you understand these terms, consider the "path" and "choice list" as attributes of each node on the decision tree, as shown with blue nodes below:

The backtrack function we define acts like a pointer, traversing this tree while correctly maintaining each node's attributes. When it reaches a leaf node, the "path" constitutes a permutation.

Further, how do we traverse a tree? It shouldn't be hard. Recall the framework of Learning Data Structures with a Systematic Approach, where various search problems are essentially tree traversal problems, and the framework for traversing an n-ary tree is as follows:

void traverse(TreeNode root) {
    for (TreeNode child : root.childern) {
        // operations needed at the preorder position
        traverse(child);
        // operations needed at the postorder position
    }
}

void traverse(TreeNode* root) {
    for (TreeNode* child : root->childern) {
        // operations needed at the preorder position
        traverse(child);
        // operations needed at the postorder position
    }
}

def traverse(root: TreeNode):
    for child in root.children:
        # operations needed at the preorder position
        traverse(child)
        # operations needed at the postorder position

func traverse(root *TreeNode) {
    for _, child := range root.children {
        // operations needed at the preorder position
        traverse(child)
        // operations needed at the postorder position
    }
}

var traverse = function(root) {
    for (var i = 0; i < root.children.length; i++) {
        // operations needed at the preorder position
        traverse(root.children[i]);
        // operations needed at the postorder position
    }
}

Regarding pre-order and post-order traversals, they represent two significant time points. Here's a diagram to illustrate:

Pre-order traversal code executes at the time point before entering a node, while post-order traversal code executes after leaving a node.

Recall our earlier discussion: "path" and "choice" are attributes of each node. As the function traverses the tree, it must correctly handle these node attributes. This involves taking actions at these two specific time points:

Do you now understand the core framework of the backtracking algorithm?

for choice in choice_list:
    # make a choice
    remove the choice from the choice list
    path.add(choice)
    backtrack(path, choice_list)
    # undo the choice
    path.remove(choice)
    re-add the choice to the choice list

By making a choice before the recursive call and undoing it afterward, we can correctly manage the choice list and path for each node.

Next, let's directly examine the code for generating permutations:

class Solution {
    List<List<Integer>> res = new LinkedList<>();

    // main function, input a set of non-repeating numbers, return all permutations
    List<List<Integer>> permute(int[] nums) {
        // record the "path"
        LinkedList<Integer> track = new LinkedList<>();
        // elements in the "path" are marked as true to avoid reuse
        boolean[] used = new boolean[nums.length];
        
        backtrack(nums, track, used);
        return res;
    }

    // path: recorded in track
    // choice list: elements not in track in nums (used[i] is false)
    // end condition: all elements in nums have appeared in track
    void backtrack(int[] nums, LinkedList<Integer> track, boolean[] used) {
        // trigger the end condition
        if (track.size() == nums.length) {
            res.add(new LinkedList(track));
            return;
        }
        
        for (int i = 0; i < nums.length; i++) {
            // exclude illegal choices
            if (used[i]) {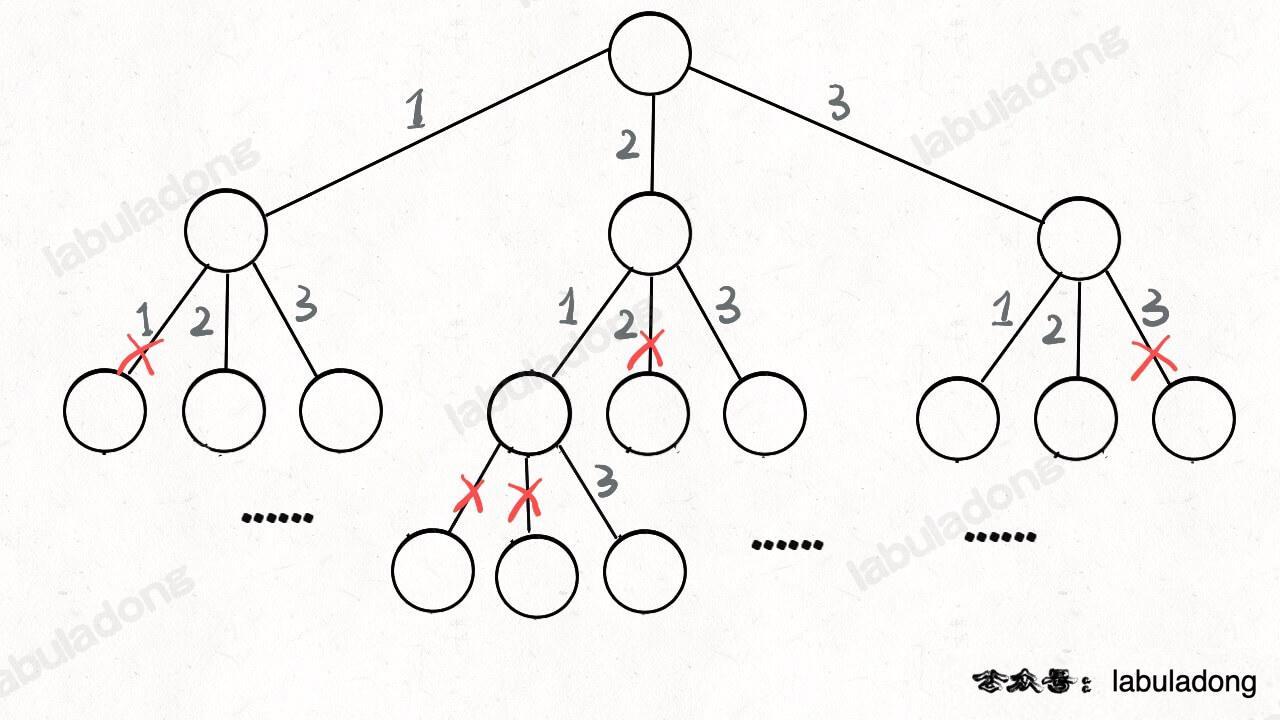

                // nums[i] is already in track, skip
                continue;
            }
            // make a choice
            track.add(nums[i]);
            used[i] = true;
            // go to the next level of decision tree
            backtrack(nums, track, used);
            // cancel the choice
            track.removeLast();
            used[i] = false;
        }
    }
}

class Solution {
private:
    vector<vector<int>> res;
public:
    // main function, input a set of non-repeating numbers, return all permutations
    vector<vector<int>> permute(vector<int>& nums) {
        // record the "path"
        vector<int> track;
        // elements in the "path" are marked as true to avoid reuse
        vector<bool> used(nums.size(), false);

        backtrack(nums, track, used);
        return res;
    }

    // path: recorded in track
    // choice list: elements not in track in nums
    // end condition: all elements in nums have appeared in track
    void backtrack(vector<int>& nums, vector<int>& track, vector<bool>& used) {
        // trigger the end condition
        if (track.size() == nums.size()) {
            res.push_back(track);
            return;
        }

        for (int i = 0; i < nums.size(); i++) {
            // exclude illegal choices
            if (used[i]) {

                // nums[i] is already in track, skip
                continue;
            }
            // make a choice
            track.push_back(nums[i]);
            used[i] = true;
            // enter the next level of decision tree
            backtrack(nums, track, used);
            // cancel the choice
            track.pop_back();
            used[i] = false;
        }
    }
};

from typing import List

class Solution:
    def __init__(self):
        self.res = []

    # main function, input a group of non-repeating numbers, return all permutations
    def permute(self, nums: List[int]) -> List[List[int]]:
        # record the "path"
        track = []
        # elements in the "path" are marked as true to avoid reuse
        used = [False] * len(nums)
        
        self.backtrack(nums, track, used)
        return self.res

    # path: recorded in track
    # choice list: elements not in track in nums (used[i] is false)
    # end condition: all elements in nums are present in track
    def backtrack(self, nums: List[int], track: List[int], used: List[bool]):
        # trigger end condition
        if len(track) == len(nums):
            self.res.append(track.copy())
            return
        
        for i in range(len(nums)):
            # exclude invalid choices
            if used[i]: 

                # nums[i] is already in track, skip
                continue
            # make a choice
            track.append(nums[i])
            used[i] = True
            # enter the next level of decision tree
            self.backtrack(nums, track, used)
            # cancel the choice
            track.pop()
            used[i] = False

func permute(nums []int) [][]int {
    res := [][]int{}
    track := []int{}
    used := make([]bool, len(nums))
    
    backtrack(nums, track, used, &res)
    return res
}

// path: recorded in track
// choice list: elements in nums that are not in track
// termination condition: all elements in nums have appeared in track
func backtrack(nums []int, track []int, used []bool, res *[][]int) {
    // trigger the termination condition
    if len(track) == len(nums) {
        // since track is a global variable, a new
        // array needs to be created to store a
        temp := make([]int, len(track))
        copy(temp, track)
        *res = append(*res, temp)
        return
    }
    
    for i := range nums {
        // exclude illegal choices
        if used[i] {

            // pruning to avoid reusing the same number
            continue
        }
        // make a choice
        track = append(track, nums[i])
        used[i] = true
        // go to the next level of the decision tree
        backtrack(nums, track, used, res)
        // cancel the choice
        track = track[:len(track)-1]
        used[i] = false
    }
}

var permute = function(nums) {
    let res = [];
    let track = [];
    let used = new Array(nums.length).fill(false);

    // path: recorded in track
    // choice list: elements in nums that are not in track
    // end condition: all elements in nums have appeared in track
    const backtrack = (nums, track, used) => {
        // trigger the end condition
        if (track.length === nums.length) {
            res.push(track.slice());
            return;
        }

        for (let i = 0; i < nums.length; i++) {
            // exclude illegal choices
            if (used[i]) {

                // pruning to avoid using the same number repeatedly
                continue;
            }
            // make a choice
            track.push(nums[i]);
            used[i] = true;
            // go to the next level of the decision tree
            backtrack(nums, track, used);
            // cancel the choice
            track.pop();
            used[i] = false;
        }
    }

    backtrack(nums, track, used);
    return res;
};

Here, we made some adjustments by not explicitly recording the "choice list." Instead, we use an used array to exclude elements already in track, thereby deriving the current choice list:

With this, we have explained the underlying principles of the backtracking algorithm through the permutation problem. Of course, this algorithm is not the most efficient for solving permutations. You might encounter solutions that do not use the used array and achieve the goal by swapping elements. However, those solutions are slightly harder to understand, which I will introduce in Ball and Box Model: Two Perspectives of Backtracking.

It is important to note that no matter how you optimize, the solutions all adhere to the backtracking framework, and the time complexity cannot be lower than O(N!) because exhaustive traversal of the entire decision tree is unavoidable. In the end, you must enumerate N! permutation results.

This is also a characteristic of the backtracking algorithm. Unlike dynamic programming, which can optimize overlapping subproblems, the backtracking algorithm is purely brute-force enumeration, generally with high complexity.

Final Summary

The backtracking algorithm is essentially a traversal problem of a multi-branch tree. The key is to perform some operations at the positions of pre-order and post-order traversal. The algorithm framework is as follows:

def backtrack(...):
    for choice in choice_list:
        make_choice
        backtrack(...)
        undo_choice

When writing the backtrack function, you need to maintain the "path" that has been taken and the current "choice list." When the "end condition" is triggered, record the "path" in the result set.

If you think about it, isn't the backtracking algorithm somewhat similar to dynamic programming? In our articles on dynamic programming, we repeatedly emphasized that the three key points are "state," "choice," and "base case," which correspond to the "path" taken, the current "choice list," and the "end condition"?

Both dynamic programming and backtracking algorithms abstract problems into tree structures at their core, but their approaches are entirely different. In Binary Tree Methodology (Guiding Principles), you will see a deeper comparison and connection between dynamic programming and backtracking algorithms.