One Method to Solve all Stock Problems on LeetCode

Many readers complain that there are too many solutions to the stock series problems on LeetCode. If you encounter such problems in an interview, you probably won't think of those clever methods. So what should you do? Therefore, this article does not focus on overly clever approaches but instead adopts a solid and steady method to solve all problems with a universal approach, meeting changes with constancy.

This article refers to the ideas from the highly-rated English solution and uses the state machine technique to solve the problems, which can pass all submissions. Don't be intimidated by this term; it's just a literary expression. In reality, it's just a DP table, and you'll understand it at a glance.

Let's randomly pick a problem and look at other people's solutions:

int maxProfit(int[] prices) {
    if(prices.empty()) return 0;
    int s1 = -prices[0], s2 = INT_MIN, s3 = INT_MIN, s4 = INT_MIN;

    for(int i = 1; i < prices.size(); ++i) {            
        s1 = max(s1, -prices[i]);
        s2 = max(s2, s1 + prices[i]);
        s3 = max(s3, s2 - prices[i]);
        s4 = max(s4, s3 + prices[i]);
    }
    return max(0, s4);
}

Can you understand it? Have you solved it yet? Probably not; it's normal if you don't understand it. Even if you barely grasp it, you might still struggle with the next problem. Why can others write such complex yet efficient solutions? Because these types of problems have a framework, but no one will tell you. Once you know, you can learn it in five minutes, and the algorithm problem loses its mystery and becomes easy to tackle.

This article will reveal that framework and guide you through solving problems swiftly. We will use state machine techniques to solve these problems, allowing you to submit all of them successfully. Don't be intimidated by the term; it's just a literary term for a DP table, which becomes clear at a glance.

These six problems share similarities. We only need to extract LeetCode problem 188, "Best Time to Buy and Sell Stock IV" for analysis, as it is the most generalized form. Other problems are simplified versions of this form. Let's look at the problem:

Input: k = 2, prices = [2,4,1]
Output: 2
Explanation: Buy on day 1 (price = 2) and sell on day 2 (price = 4), profit = 4-2 = 2.

Input: k = 2, prices = [3,2,6,5,0,3]
Output: 7
Explanation: Buy on day 2 (price = 2) and sell on day 3 (price = 6), profit = 6-2 = 4. Then buy on day 5 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.

The first problem involves making only one transaction, equivalent to k = 1. The second problem allows unlimited transactions, equivalent to k = +infinity (positive infinity). The third problem involves exactly two transactions, equivalent to k = 2. The remaining two problems also allow unlimited transactions but add extra conditions of a "cool-down period" and a "transaction fee," which are variations of the second problem and are easy to handle.

Now, let's get back to the main topic and start solving.

1. Brute-Force Framework

First, let's consider the same question: How to enumerate all possibilities?

As mentioned in Dynamic Programming Core Techniques, dynamic programming algorithms essentially enumerate all possible "states" and then select the optimal solution from the "choices".

For this problem, let's break it down day by day to identify all possible "states" and the corresponding "choices" for each state. We need to enumerate all "states" to update them based on the corresponding "choices". This might sound abstract, but just remember the terms "state" and "choice". It will become clear with a practical example.

for state1 in all_values_of_state1:
    for state2 in all_values_of_state2:
        for ...
            dp[state1][state2][...] = optimize(choice1, choice2, ...)

For instance, in this problem, there are three "choices" available each day: buy, sell, and do nothing (rest). We represent these choices with buy, sell, and rest.

However, not all choices are available every day. For example, sell must follow buy, and buy must follow sell. Therefore, the rest operation should be divided into two states: one after buy (holding a stock) and one after sell (not holding a stock). Additionally, we have a limit on the number of transactions k, meaning buy can only be executed if k > 0.

Sounds complicated, right? Don't worry. Our goal right now is just to enumerate everything. No matter how many states you have, my job is to list them all out in one go.

This problem has three "states": the first is the number of days, the second is the maximum number of transactions allowed, and the third is the current holding state (i.e., the previously mentioned rest state, which we can represent as 1 for holding and 0 for not holding). We can use a three-dimensional array to store all combinations of these states:

dp[i][k][0 or 1]
0 <= i <= n - 1, 1 <= k <= K
n is the number of days, K is the upper limit of transactions, and 0 and 1 represent whether you hold a stock.
This problem has n × K × 2 states in total, and we can solve it by enumerating all of them.

for 0 <= i < n:
    for 1 <= k <= K:
        for s in {0, 1}:
            dp[i][k][s] = max(buy, sell, rest)

Moreover, we can describe the meaning of each state in natural language. For example, dp[3][2][1] means: it's the third day, I currently hold a stock, and I have made at most 2 transactions so far. Another example, dp[2][3][0] means: it's the second day, I currently do not hold any stock, and I have made at most 3 transactions so far. It's quite easy to understand, right?

The final answer we want is dp[n - 1][K][0], which means on the last day, with at most K transactions allowed, the maximum profit we can achieve.

You might wonder why not dp[n - 1][K][1]? Because dp[n - 1][K][1] means holding a stock on the last day, while dp[n - 1][K][0] means the stock has been sold by the last day. Obviously, the latter will yield a higher profit than the former.

Remember how to interpret "states". Whenever you find something hard to understand, translating it into natural language can make it easier to grasp.

II. State Transition Framework

Having completed the exhaustive enumeration of "states," we now consider the "choices" available for each "state" and how to update these "states."

Focusing on the "holding state," we can illustrate a state transition diagram:

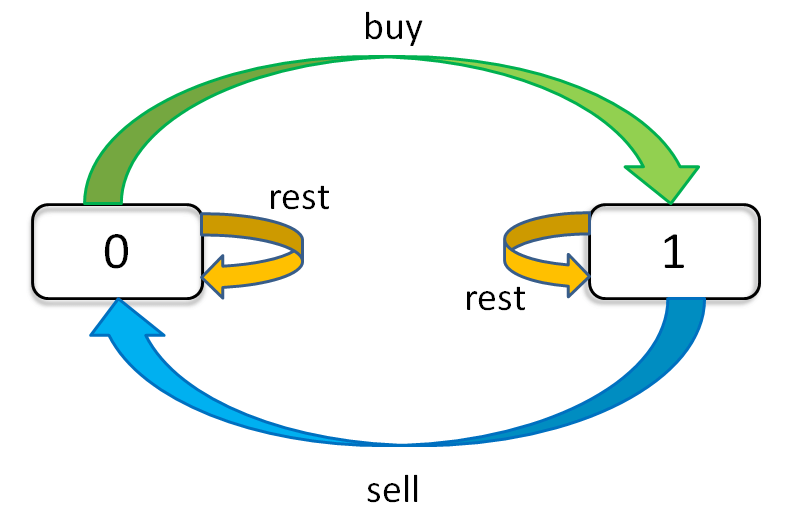
This diagram clearly shows how each state (0 and 1) transitions. Based on this diagram, we can write the state transition equations:

dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
              max( choose rest today,        choose sell today       )

Explanation: Today, I do not hold any stock. There are two possibilities, and I seek the maximum profit from these:

1. I did not hold any stock yesterday, with a maximum transaction limit of k up to yesterday; then I choose rest today, so I still do not hold any stock today, and the maximum transaction limit remains k.

2. I held a stock yesterday, with a maximum transaction limit of k up to yesterday; but I sell today, so I do not hold any stock today, and the maximum transaction limit remains k.

dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
              max( choose rest today,         choose buy today         )

Explanation: Today, I hold a stock with a maximum transaction limit of k. For yesterday, there are two possibilities, and I seek the maximum profit from these:

1. I held a stock yesterday, with a maximum transaction limit of k; then I choose rest today, so I still hold the stock today, and the maximum transaction limit remains k.

2. I did not hold any stock yesterday, with a maximum transaction limit of k - 1; but I choose buy today, so I hold a stock today, and the maximum transaction limit is k.

This explanation should be clear: if you buy, subtract prices[i] from the profit; if you sell, add prices[i] to the profit. The maximum profit today is the larger of these two choices.

Note the limit of k: choosing buy effectively starts a new transaction, so for yesterday, the upper limit of transactions k should decrease by 1.

Now, we have completed the most challenging step in dynamic programming: the state transition equation. If you understood the previous content, you can already solve all problems quickly by applying this framework. However, there's one last bit missing, which is defining the base case, the simplest scenario.

dp[-1][...][0] = 0
Explanation: Since `i` starts from 0, `i = -1` means we haven't started yet, so the profit is naturally 0.

dp[-1][...][1] = -infinity
Explanation: Before we start, it's impossible to hold any stock.
Since our algorithm requires a maximum value, we set the initial value to the smallest possible value to easily find the maximum.

dp[...][0][0] = 0
Explanation: Since `k` starts from 1, `k = 0` means no transactions are allowed, so the profit is naturally 0.

dp[...][0][1] = -infinity
Explanation: When no transactions are allowed, it's impossible to hold any stock.
Again, we set the initial value to the smallest possible value for ease of finding the maximum.

Summarizing the state transition equations:

Base case:
dp[-1][...][0] = dp[...][0][0] = 0
dp[-1][...][1] = dp[...][0][1] = -infinity

State transition equations:
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])

You might be wondering how to represent an array index of -1 in programming, or how to represent negative infinity. These are detail issues and there are many ways to handle them. Now that the complete framework is in place, let's move on to specific examples.

3. Quick Solve Problems

121. Best Time to Buy and Sell Stock

First, let's discuss LeetCode Problem 121: Best Time to Buy and Sell Stock, which is equivalent to the case of k = 1:

Input: prices = [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.

Input: prices = [7,6,4,3,1]
Output: 0
Explanation: In this case, no transactions are done and the max profit = 0.

Directly apply the state transition equations. Based on the base case, we can simplify:

dp[i][1][0] = max(dp[i-1][1][0], dp[i-1][1][1] + prices[i])
dp[i][1][1] = max(dp[i-1][1][1], dp[i-1][0][0] - prices[i]) 
            = max(dp[i-1][1][1], -prices[i])
Explanation: In the base case of k = 0, dp[i-1][0][0] = 0.

Now, we notice that k is always 1 and does not change, meaning k no longer affects state transitions. We can simplify further by removing all k:
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], -prices[i])

Directly write the code:

int n = prices.length;
int[][] dp = new int[n][2];
for (int i = 0; i < n; i++) {
    dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
    dp[i][1] = Math.max(dp[i-1][1], -prices[i]);
}
return dp[n - 1][0];

int n = prices.size();
vector<vector<int>> dp(n, vector<int>(2));
dp[0][0] = 0;
dp[0][1] = -prices[0];

for (int i = 1; i < n; ++i) {
    dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
    dp[i][1] = max(dp[i-1][1], -prices[i]);
}

return dp[n-1][0];

n = len(prices)
dp = [[0]*2 for _ in range(n)]
for i in range(n):
    dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
    dp[i][1] = max(dp[i-1][1], -prices[i])
return dp[n - 1][0]

n := len(prices)
dp := make([][2]int, n)
for i := 0; i < n; i++ {
    if i == 0 {
        dp[i][0] = 0
        dp[i][1] = -prices[i]
        continue
    }
    dp[i][0] = max(dp[i-1][0], dp[i-1][1]+prices[i])
    dp[i][1] = max(dp[i-1][1], -prices[i])
}
return dp[n-1][0]

var n = prices.length;
var dp = Array.from({ length: n }, () => new Array(2).fill(0));
for (var i = 0; i < n; i++) {
    dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
    dp[i][1] = Math.max(dp[i-1][1], -prices[i]);
}
return dp[n - 1][0];

Clearly, when i = 0, i - 1 is an invalid index. This is because we haven't handled the base case for i. We can give a special treatment like this:

if (i - 1 == -1) {
    dp[i][0] = 0;
    // According to the state transition equation:
    //   dp[i][0] 
    // = max(dp[-1][0], dp[-1][1] + prices[i])
    // = max(0, -infinity + prices[i]) = 0
    //   dp[i][0] 
    // = max(dp[-1][0], dp[-1][1] + prices[i])
    // = max(0, -infinity + prices[i]) = 0

    dp[i][1] = -prices[i];
    // According to the state transition equation:
    //   dp[i][1] 
    // = max(dp[-1][1], dp[-1][0] - prices[i])
    // = max(-infinity, 0 - prices[i]) 
    // = -prices[i]
    //   dp[i][1] 
    // = max(dp[-1][1], dp[-1][0] - prices[i])
    // = max(-infinity, 0 - prices[i]) 
    // = -prices[i]
    continue;
}

The first problem is solved, but handling the base case this way is quite troublesome. Also, notice the state transition equation: the new state only depends on the adjacent state. Therefore, we can use the technique from the previous article Dimensionality Reduction in Dynamic Programming: Space Compression Techniques. Instead of using the entire dp array, we only need a single variable to store the adjacent state. This reduces the space complexity to O(1):

// Original version
int maxProfit_k_1(int[] prices) {
    int n = prices.length;
    int[][] dp = new int[n][2];
    for (int i = 0; i < n; i++) {
        if (i - 1 == -1) {
            // base case
            dp[i][0] = 0;
            dp[i][1] = -prices[i];
            continue;
        }
        dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
        dp[i][1] = Math.max(dp[i-1][1], -prices[i]);
    }
    return dp[n - 1][0];
}

// Space complexity optimized version
int maxProfit_k_1(int[] prices) {
    int n = prices.length;
    // base case: dp[-1][0] = 0, dp[-1][1] = -infinity
    int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
    for (int i = 0; i < n; i++) {
        // dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
        // dp[i][1] = max(dp[i-1][1], -prices[i])
        dp_i_1 = Math.max(dp_i_1, -prices[i]);
    }
    return dp_i_0;
}

// Original version
int maxProfit_k_1(vector<int>& prices) {
    int n = prices.size();
    vector<vector<int>> dp(n, vector<int>(2));
    for (int i = 0; i < n; i++) {
        if (i - 1 == -1) {
            // base case
            dp[i][0] = 0;
            dp[i][1] = -prices[i];
            continue;
        }
        dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
        dp[i][1] = max(dp[i-1][1], -prices[i]);
    }
    return dp[n - 1][0];
}

// Space complexity optimized version
int maxProfit_k_1(vector<int>& prices) {
    int n = prices.size();
    // base case: dp[-1][0] = 0, dp[-1][1] = -infinity
    int dp_i_0 = 0, dp_i_1 = INT_MIN;
    for (int i = 0; i < n; i++) {
        // dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        dp_i_0 = max(dp_i_0, dp_i_1 + prices[i]);
        // dp[i][1] = max(dp[i-1][1], -prices[i])
        dp_i_1 = max(dp_i_1, -prices[i]);
    }
    return dp_i_0;
}

# Original version
def maxProfit_k_1(prices: List[int]) -> int:
    n = len(prices)
    dp = [[0 for i in range(2)] for j in range(n)]
    for i in range(n):
        if i - 1 == -1:
            # base case
            dp[i][0] = 0
            dp[i][1] = -prices[i]
            continue
        dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        dp[i][1] = max(dp[i-1][1], -prices[i])
    return dp[n-1][0]

# Space complexity optimized version
def maxProfit_k_1(prices: List[int]) -> int:
    n = len(prices)
    # base case: dp[-1][0] = 0, dp[-1][1] = -infinity
    dp_i_0, dp_i_1 = 0, float('-inf')
    for i in range(n):
        # dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        dp_i_0, dp_i_1 = max(dp_i_0, dp_i_1 + prices[i]), max(dp_i_1, -prices[i])
    return dp_i_0

// Original version
func maxProfit_k_1(prices []int) int {
    n := len(prices)
    dp := make([][2]int, n)
    for i := 0; i < n; i++ {
        if i - 1 == -1 {
            // base case
            dp[i][0] = 0
            dp[i][1] = -prices[i]
            continue
        }
        dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        dp[i][1] = max(dp[i-1][1], -prices[i])
    }
    return dp[n - 1][0]
}

// Space complexity optimized version
func maxProfit_k_1(prices []int) int {
    n := len(prices)
    // base case: dp[-1][0] = 0, dp[-1][1] = -infinity
    dp_i_0, dp_i_1 := 0, -2147483648
    for i := 0; i < n; i++ {
        // dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        dp_i_0 = max(dp_i_0, dp_i_1 + prices[i])
        // dp[i][1] = max(dp[i-1][1], -prices[i])
        dp_i_1 = max(dp_i_1, -prices[i])
    }
    return dp_i_0
}

var maxProfit_k_1 = function(prices) {
    var n = prices.length;
    var dp = new Array(n).fill(0).map(() => new Array(2).fill(0));
    for (var i = 0; i < n; i++) {
        if (i - 1 == -1) {
            // base case
            dp[i][0] = 0;
            dp[i][1] = -prices[i];
            continue;
        }
        dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
        dp[i][1] = Math.max(dp[i-1][1], -prices[i]);
    }
    return dp[n - 1][0];
};

// version optimized for space complexity
var maxProfit_k_1 = function(prices) {
    var n = prices.length;
    // base case: dp[-1][0] = 0, dp[-1][1] = negative infinity
    var dp_i_0 = 0, dp_i_1 = -Infinity;
    for (var i = 0; i < n; i++) {
        // dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
        // dp[i][1] = max(dp[i-1][1], -prices[i])
        dp_i_1 = Math.max(dp_i_1, -prices[i]);
    }
    return dp_i_0;
};

Both methods are the same, but this programming approach is much more concise. However, without the guidance of the previous state transition equation, it would be impossible to understand. In the subsequent problems, you can compare how to optimize the space of the dp array.

122. Best Time to Buy and Sell Stock II

The second problem, let's look at LeetCode problem 122: "Best Time to Buy and Sell Stock II", which is the case where k is infinite:

Input: prices = [7,1,5,3,6,4]
Output: 7
Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.
Total profit is 4 + 3 = 7.

Input: prices = [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Total profit is 4.

Input: prices = [7,6,4,3,1]
Output: 0
Explanation: There is no way to make a positive profit, so we never buy the stock to achieve the maximum profit of 0.

The problem specifically emphasizes that you can sell on the same day, but I think this condition is purely redundant. If you buy and sell on the same day, the profit is obviously 0, which is the same as not making a transaction at all. The characteristic of this problem is that there is no limit on the total number of transactions k, which is equivalent to k being infinite.

If k is infinite, then k and k - 1 are essentially the same. The framework can be rewritten as follows:

dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
            = max(dp[i-1][k][1], dp[i-1][k][0] - prices[i])

We find that `k` in the array no longer changes, meaning there's no need to track the state of `k`:
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])

Directly translated into code:

// Original version
int maxProfit_k_inf(int[] prices) {
    int n = prices.length;
    int[][] dp = new int[n][2];
    for (int i = 0; i < n; i++) {
        if (i - 1 == -1) {
            // base case
            dp[i][0] = 0;
            dp[i][1] = -prices[i];
            continue;
        }
        dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
        dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i]);
    }
    return dp[n - 1][0];
}

// Space complexity optimized version
int maxProfit_k_inf(int[] prices) {
    int n = prices.length;
    int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
    for (int i = 0; i < n; i++) {
        int temp = dp_i_0;
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
        dp_i_1 = Math.max(dp_i_1, temp - prices[i]);
    }
    return dp_i_0;
}

// Original version
int maxProfit_k_inf(vector<int>& prices) {
    int n = prices.size();
    vector<vector<int>> dp(n, vector<int>(2, 0));
    for (int i = 0; i < n; i++) {
        if (i - 1 == -1) {
            // base case
            dp[i][0] = 0;
            dp[i][1] = -prices[i];
            continue;
        }
        dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
        dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i]);
    }
    return dp[n - 1][0];
}

// Space complexity optimization version
int maxProfit_k_inf(vector<int>& prices) {
    int n = prices.size();
    int dp_i_0 = 0, dp_i_1 = INT_MIN;
    for (int i = 0; i < n; i++) {
        int temp = dp_i_0;
        dp_i_0 = max(dp_i_0, dp_i_1 + prices[i]);
        dp_i_1 = max(dp_i_1, temp - prices[i]);
    }
    return dp_i_0;
}

# Original version
class Solution:
    def maxProfit_k_inf(self, prices: List[int]) -> int:
        n = len(prices)
        dp = [[0]*2 for _ in range(n)]
        for i in range(n):
            if i - 1 == -1:
                # base case
                dp[i][0] = 0
                dp[i][1] = -prices[i]
                continue
            dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
            dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])
        return dp[n - 1][0]

# Space complexity optimized version
class Solution:
    def maxProfit_k_inf(self, prices: List[int]) -> int:
        n = len(prices)
        dp_i_0, dp_i_1 = 0, float('-inf')
        for i in range(n):
            temp = dp_i_0
            dp_i_0 = max(dp_i_0, dp_i_1 + prices[i])
            dp_i_1 = max(dp_i_1, temp - prices[i])
        return dp_i_0

// Original version
func maxProfit(prices []int) int {
    n := len(prices)
    dp := make([][2]int, n)
    for i := 0; i < n; i++ {
        if i - 1 == -1 {
            dp[i][0] = 0
            dp[i][1] = -prices[i]
            continue
        }
        dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])
    }
    return dp[n-1][0]
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

// Space complexity optimized version
func maxProfit(prices []int) int {
    n := len(prices)
    dp_i_0, dp_i_1 := 0, math.MinInt32
    for i := 0; i < n; i++ {
        temp := dp_i_0
        dp_i_0 = max(dp_i_0, dp_i_1 + prices[i])
        dp_i_1 = max(dp_i_1, temp - prices[i])
    }
    return dp_i_0
}

// Original version
var maxProfit_k_inf = function(prices) {
    var n = prices.length;
    var dp = Array.from(Array(n), () => Array(2).fill(0));
    for (var i = 0; i < n; i++) {
        if (i - 1 == -1) {
            // base case
            dp[i][0] = 0;
            dp[i][1] = -prices[i];
            continue;
        }
        dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
        dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
    }
    return dp[n - 1][0];
}

// Space complexity optimized version
var maxProfit_k_inf = function(prices) {
    var n = prices.length;
    var dp_i_0 = 0, dp_i_1 = Number.MIN_VALUE;
    for (var i = 0; i < n; i++) {
        var temp = dp_i_0;
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
        dp_i_1 = Math.max(dp_i_1, temp - prices[i]);
    }
    return dp_i_0;
}

309. Best Time to Buy and Sell Stock with Cooldown

For the third problem, refer to LeetCode Problem 309: "Best Time to Buy and Sell Stock with Cooldown", which is the case where k is infinite, but includes a cooldown period after each transaction:

Input: prices = [1,2,3,0,2]
Output: 3
Explanation: transactions = [buy, sell, cooldown, buy, sell]

Input: prices = [1]
Output: 0

Similar to the previous problem, but after each sell, you have to wait a day before you can trade again. Simply incorporate this feature into the state transition equation from the previous problem:

dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i])
Explanation: On day i, if you choose to buy, transition from the state of i-2, not i-1.

Translated into code:

// Original version
int maxProfit_with_cool(int[] prices) {
    int n = prices.length;
    int[][] dp = new int[n][2];
    for (int i = 0; i < n; i++) {
        if (i - 1 == -1) {
            // base case 1
            dp[i][0] = 0;
            dp[i][1] = -prices[i];
            continue;
        }
        if (i - 2 == -1) {
            // base case 2
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
            // when i - 2 is less than 0, derive the
            // corresponding base case based on the state
            dp[i][1] = Math.max(dp[i-1][1], -prices[i]);
            //   dp[i][1] 
            // = max(dp[i-1][1], dp[-1][0] - prices[i])
            // = max(dp[i-1][1], 0 - prices[i])
            // = max(dp[i-1][1], -prices[i])
            continue;
        }
        dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
        dp[i][1] = Math.max(dp[i-1][1], dp[i-2][0] - prices[i]);
    }
    return dp[n - 1][0];
}

// Space complexity optimization version
int maxProfit_with_cool(int[] prices) {
    int n = prices.length;
    int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
    // represents dp[i-2][0]
    int dp_pre_0 = 0;
    for (int i = 0; i < n; i++) {
        int temp = dp_i_0;
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
        dp_i_1 = Math.max(dp_i_1, dp_pre_0 - prices[i]);
        dp_pre_0 = temp;
    }
    return dp_i_0;
}

// Original version
int maxProfit_with_cool(vector<int>& prices) {
    int n = prices.size();
    vector<vector<int>> dp(n, vector<int>(2));
    for (int i = 0; i < n; i++) {
        if (i - 1 == -1) {
            // base case 1
            dp[i][0] = 0;
            dp[i][1] = -prices[i];
            continue;
        }
        if (i - 2 == -1) {
            // base case 2
            dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
            // when i - 2 is less than 0, derive the
            // corresponding base case according to the state
            dp[i][1] = max(dp[i-1][1], -prices[i]);
            //   dp[i][1] 
            // = max(dp[i-1][1], dp[-1][0] - prices[i])
            // = max(dp[i-1][1], 0 - prices[i])
            // = max(dp[i-1][1], -prices[i])
            continue;
        }
        dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
        dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i]);
    }
    return dp[n - 1][0];
}

// Space complexity optimization version
int maxProfit_with_cool(vector<int>& prices) {
    int n = prices.size();
    int dp_i_0 = 0, dp_i_1 = INT_MIN;
    // represents dp[i-2][0]
    int dp_pre_0 = 0;
    for (int i = 0; i < n; i++) {
        int temp = dp_i_0;
        dp_i_0 = max(dp_i_0, dp_i_1 + prices[i]);
        dp_i_1 = max(dp_i_1, dp_pre_0 - prices[i]);
        dp_pre_0 = temp;
    }
    return dp_i_0;
}

# Original version
def maxProfit_with_cool(prices: List[int]) -> int:
    n = len(prices)
    dp = [[0] * 2 for _ in range(n)]
    for i in range(n):
        if i - 1 == -1:
            # base case 1
            dp[i][0] = 0
            dp[i][1] = -prices[i]
            continue
        if i - 2 == -1:
            # base case 2
            dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
            # When i = 1, dp[i-2] is not valid, so we can only transition from dp[i-1][1]
            dp[i][1] = max(dp[i-1][1], -prices[i])
            # Explanation as above
            continue
        dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i])
    return dp[n-1][0]

# Space complexity optimized version
def maxProfit_with_cool(prices: List[int]) -> int:
    n = len(prices)
    dp_i_0, dp_i_1, dp_pre_0 = 0, float('-inf'), 0
    for i in range(n):
        temp = dp_i_0
        dp_i_0 = max(dp_i_0, dp_i_1 + prices[i])
        dp_i_1 = max(dp_i_1, dp_pre_0 - prices[i])
        dp_pre_0 = temp
    return dp_i_0

// Original version
func maxProfit_with_cool(prices []int) int {
    n := len(prices)
    dp := make([][2]int, n)
    for i := 0; i < n; i++ {
        if i - 1 == -1 {
            // base case 1
            dp[i][0] = 0
            dp[i][1] = -prices[i]
            continue
        }
        if i - 2 == -1 {
            // base case 2
            dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
            // when i - 2 is less than 0, derive the
            // corresponding base case based on the state
            dp[i][1] = max(dp[i-1][1], -prices[i])
            //   dp[i][1] 
            // = max(dp[i-1][1], dp[-1][0] - prices[i])
            // = max(dp[i-1][1], 0 - prices[i])
            // = max(dp[i-1][1], -prices[i])
            continue
        }
        dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i])
    }
    return dp[n - 1][0]
}

// Space complexity optimization version
func maxProfit_with_cool(prices []int) int {
    n := len(prices)
    dp_i_0, dp_i_1 := 0, math.MinInt32
    // represents dp[i-2][0]
    dp_pre_0 := 0
    for i := 0; i < n; i++ {
        temp := dp_i_0
        dp_i_0 = max(dp_i_0, dp_i_1 + prices[i])
        dp_i_1 = max(dp_i_1, dp_pre_0 - prices[i])
        dp_pre_0 = temp
    }
    return dp_i_0
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

var maxProfit_with_cool = function(prices) {
    let n = prices.length;
    let dp = new Array(n).fill(null).map(() => new Array(2).fill(0));
    for (let i = 0; i < n; i++) {
        if (i - 1 == -1) {
            // base case 1
            dp[i][0] = 0;
            dp[i][1] = -prices[i];
            continue;
        }
        if (i - 2 == -1) {
            // base case 2
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
            // when i - 2 is less than 0, derive the
            // corresponding base case based on the state
            dp[i][1] = Math.max(dp[i-1][1], -prices[i]);
            //   dp[i][1] 
            // = max(dp[i-1][1], dp[-1][0] - prices[i])
            // = max(dp[i-1][1], 0 - prices[i])
            // = max(dp[i-1][1], -prices[i])
            continue;
        }
        dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
        dp[i][1] = Math.max(dp[i-1][1], dp[i-2][0] - prices[i]);
    }
    return dp[n - 1][0];
};

var maxProfit_with_cool = function(prices) {
    let n = prices.length;
    let dp_i_0 = 0;
    let dp_i_1 = Number.MIN_SAFE_INTEGER;
    // represents dp[i-2][0]
    let dp_pre_0 = 0;
    for (let i = 0; i < n; i++) {
        let temp = dp_i_0;
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
        dp_i_1 = Math.max(dp_i_1, dp_pre_0 - prices[i]);
        dp_pre_0 = temp;
    }
    return dp_i_0;
};

714. 买卖股票的最佳时机含手续费

For the fourth problem, refer to LeetCode Problem 714: "Best Time to Buy and Sell Stock with Transaction Fee", which considers the case where k is infinity and transaction fees are involved:

Input: prices = [1,3,2,8,4,9], fee = 2
Output: 8
Explanation: The maximum profit can be achieved by:
- Buying at prices[0] = 1
- Selling at prices[3] = 8
- Buying at prices[4] = 4
- Selling at prices[5] = 9
The total profit is ((8 - 1) - 2) + ((9 - 4) - 2) = 8.

Input: prices = [1,3,7,5,10,3], fee = 3
Output: 6

A fee is charged for each transaction, simply subtract the fee from the profit to rewrite the equation:

dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i] - fee)
Explanation: It is equivalent to increasing the buying price of the stock.
Subtracting in the first equation is the same as reducing the selling price of the stock.

Translate directly into code, note that after changing the state transition equation, the base case must also be adjusted accordingly:

// Original version
int maxProfit_with_fee(int[] prices, int fee) {
    int n = prices.length;
    int[][] dp = new int[n][2];
    for (int i = 0; i < n; i++) {
        if (i - 1 == -1) {
            // base case
            dp[i][0] = 0;
            dp[i][1] = -prices[i] - fee;
            //   dp[i][1]
            // = max(dp[i - 1][1], dp[i - 1][0] - prices[i] - fee)
            // = max(dp[-1][1], dp[-1][0] - prices[i] - fee)
            // = max(-inf, 0 - prices[i] - fee)
            // = -prices[i] - fee
            continue;
        }
        dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
        dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i] - fee);
    }
    return dp[n - 1][0];
}

// Space complexity optimization version
int maxProfit_with_fee(int[] prices, int fee) {
    int n = prices.length;
    int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE;
    for (int i = 0; i < n; i++) {
        int temp = dp_i_0;
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
        dp_i_1 = Math.max(dp_i_1, temp - prices[i] - fee);
    }
    return dp_i_0;
}

// Original version
int maxProfit_with_fee(vector<int>& prices, int fee) {
    int n = prices.size();
    vector<vector<int>> dp(n, vector<int>(2));
    for (int i = 0; i < n; i++) {
        if (i - 1 == -1) {
            // base case
            dp[i][0] = 0;
            dp[i][1] = -prices[i] - fee;
            //   dp[i][1]
            // = max(dp[i - 1][1], dp[i - 1][0] - prices[i] - fee)
            // = max(dp[-1][1], dp[-1][0] - prices[i] - fee)
            // = max(-inf, 0 - prices[i] - fee)
            // = -prices[i] - fee
            continue;
        }
        dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
        dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i] - fee);
    }
    return dp[n - 1][0];
}

// Space complexity optimization version
int maxProfit_with_fee(vector<int>& prices, int fee) {
    int n = prices.size();
    int dp_i_0 = 0, dp_i_1 = INT_MIN;
    for (int i = 0; i < n; i++) {
        int temp = dp_i_0;
        dp_i_0 = max(dp_i_0, dp_i_1 + prices[i]);
        dp_i_1 = max(dp_i_1, temp - prices[i] - fee);
    }
    return dp_i_0;
}

# Original version
def maxProfit_with_fee(prices: List[int], fee: int) -> int:
    n = len(prices)
    dp = [[0] * 2 for _ in range(n)]
    for i in range(n):
        if i - 1 == -1:
            # base case
            dp[i][0] = 0
            dp[i][1] = -prices[i] - fee
            #   dp[i][1]
            # = max(dp[i - 1][1], dp[i - 1][0] - prices[i] - fee)
            # = max(dp[-1][1], dp[-1][0] - prices[i] - fee)
            # = max(-inf, 0 - prices[i] - fee)
            # = -prices[i] - fee
            continue
        dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i])
        dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i] - fee)
    return dp[n - 1][0]

# Space complexity optimized version
def maxProfit_with_fee(prices: List[int], fee: int) -> int:
    n = len(prices)
    dp_i_0, dp_i_1 = 0, float('-inf')
    for i in range(n):
        temp = dp_i_0
        dp_i_0 = max(dp_i_0, dp_i_1 + prices[i])
        dp_i_1 = max(dp_i_1, temp - prices[i] - fee)
    return dp_i_0

// Original version
func maxProfit_with_fee(prices []int, fee int) int {
    n := len(prices)
    dp := make([][2]int, n)
    for i := 0; i < n; i++ {
        if i - 1 == -1 {
            // base case
            dp[i][0] = 0
            dp[i][1] = -prices[i] - fee
            //   dp[i][1]
            // = max(dp[i - 1][1], dp[i - 1][0] - prices[i] - fee)
            // = max(dp[-1][1], dp[-1][0] - prices[i] - fee)
            // = max(-inf, 0 - prices[i] - fee)
            // = -prices[i] - fee
            continue
        }
        dp[i][0] = Max(dp[i-1][0], dp[i-1][1]+prices[i])
        dp[i][1] = Max(dp[i-1][1], dp[i-1][0]-prices[i]-fee)
    }
    return dp[n-1][0]
}

// Space complexity optimized version
func maxProfit_with_fee(prices []int, fee int) int {
    n := len(prices)
    dp_i_0, dp_i_1 := 0, -1<<31
    for i := 0; i < n; i++ {
        temp := dp_i_0
        dp_i_0 = Max(dp_i_0, dp_i_1+prices[i])
        dp_i_1 = Max(dp_i_1, temp-prices[i]-fee)
    }
    return dp_i_0
}

func Max(x, y int) int {
    if x > y {
        return x
    }
    return y
}

var maxProfit_with_fee = function(prices, fee) {
    var n = prices.length;
    var dp = new Array(n);
    for (var i = 0; i < n; i++) {
        dp[i] = new Array(2);
        if (i - 1 == -1) {
            // initial state
            dp[i][0] = 0;
            dp[i][1] = -prices[i] - fee;
            //   dp[i][1]
            // = max(dp[i - 1][1], dp[i - 1][0] - prices[i] - fee)
            // = max(dp[-1][1], dp[-1][0] - prices[i] - fee)
            // = max(-inf, 0 - prices[i] - fee)
            // = -prices[i] - fee
            continue;
        }
        dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
        dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i] - fee);
    }
    return dp[n - 1][0];
};

var maxProfit_with_fee_2 = function(prices, fee) {
    var n = prices.length;
    var dp_i_0 = 0, dp_i_1 = Number.MIN_VALUE;
    for (var i = 0; i < n; i++) {
        var temp = dp_i_0;
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]);
        dp_i_1 = Math.max(dp_i_1, temp - prices[i] - fee);
    }
    return dp_i_0;
};

123. Best Time to Buy and Sell Stock III

The fifth question, see LeetCode Problem 123 "Best Time to Buy and Sell Stock III", which is the case of k = 2:

Input: prices = [3,3,5,0,0,3,1,4]
Output: 6
Explanation: Buy on day 4 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
Then buy on day 7 (price = 1) and sell on day 8 (price = 4), profit = 4-1 = 3.

Input: prices = [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are engaging multiple transactions at the same time. You must sell before buying again.

Input: prices = [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.

The situation with k = 2 is slightly different from the earlier problems, because in those situations the relationship with k was not very significant: either k is positive infinity, making the state transition independent of k; or k = 1, which is close to the base case of k = 0, rendering it less noticeable.

In this problem where k = 2 and in the upcoming discussion where k is any positive integer, the handling of k becomes prominent. Let's write the code and analyze the reasons as we go.

Original state transition equations, no simplification possible
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])

Based on previous code, we might naively write it like this (incorrectly):

int k = 2;
int[][][] dp = new int[n][k + 1][2];
for (int i = 0; i < n; i++) {
    if (i - 1 == -1) {
        // handle the base case
        dp[i][k][0] = 0;
        dp[i][k][1] = -prices[i];
        continue;
    }
    dp[i][k][0] = Math.max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
    dp[i][k][1] = Math.max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);
}
return dp[n - 1][k][0];

int k = 2;
vector<vector<vector<int>>> dp(n, vector<vector<int>>(k + 1, vector<int>(2)));
for (int i = 0; i < n; i++) {
    if (i - 1 == -1) {
        // handle the base case
        dp[i][k][0] = 0;
        dp[i][k][1] = -prices[i];
        continue;
    }
    dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
    dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);
}
return dp[n - 1][k][0];

k = 2
dp = [[[0 for _ in range(2)] for _ in range(k + 1)] for _ in range(n)]
for i in range(n):
    if i - 1 == -1:
        # handle the base case
        dp[i][k][0] = 0
        dp[i][k][1] = -prices[i]
        continue
    dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
    dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
return dp[n - 1][k][0]

k := 2
dp := make([][][]int, n)
for i := range dp {
    // build a 3-dimensional DP array
    dp[i] = make([][]int, k+1)
    for j := range dp[i] {
        // initialize the DP array
        dp[i][j] = make([]int, 2)
    }
}

for i := 0; i < n; i++ {
    if i-1 == -1 {
        // handle the base case
        dp[i][k][0] = 0
        dp[i][k][1] = -prices[i]
        continue
    }
    dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1]+prices[i])
    dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0]-prices[i])
}

return dp[n-1][k][0]

var k = 2;
var dp = new Array(n);
for (var i = 0; i < n; i++) {
    dp[i] = new Array(k + 1);
    for (var j = 0; j < k + 1; j++) {
        dp[i][j] = new Array(2);
    }
    if (i - 1 == -1) {
        // handle the base case
        dp[i][k][0] = 0;
        dp[i][k][1] = -prices[i];
        continue;
    }
    dp[i][k][0] = Math.max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
    dp[i][k][1] = Math.max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);
}
return dp[n - 1][k][0];

Why is it wrong? I followed the state transition equation, didn't I?

Do you remember the "Exhaustive Framework" we summarized earlier? It means we must enumerate all possible states. In fact, our previous solutions were all about enumerating all states, but in those problems, k was simplified.

For example, the code framework for the first problem when k = 1:

int n = prices.length;
int[][] dp = new int[n][2];
for (int i = 0; i < n; i++) {
    dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
    dp[i][1] = Math.max(dp[i-1][1], -prices[i]);
}
return dp[n - 1][0];

int n = prices.size();
vector<vector<int>> dp(n, vector<int>(2));
dp[0][0] = 0;
dp[0][1] = -prices[0];

for (int i = 1; i < n; ++i) {
    dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);
    dp[i][1] = max(dp[i-1][1], -prices[i]);
}

return dp[n-1][0];

# LeeCode Solution
n = len(prices)
dp = [[0]*2 for _ in range(n)]
for i in range(n):
    dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
    dp[i][1] = max(dp[i-1][1], -prices[i])
return dp[n - 1][0]