Union-Find Algorithm

The Union-Find algorithm is designed for the problem of "dynamic connectivity". It is tested very often, and you must master it.

First, let’s talk about what dynamic connectivity in a graph means.

1. Dynamic Connectivity

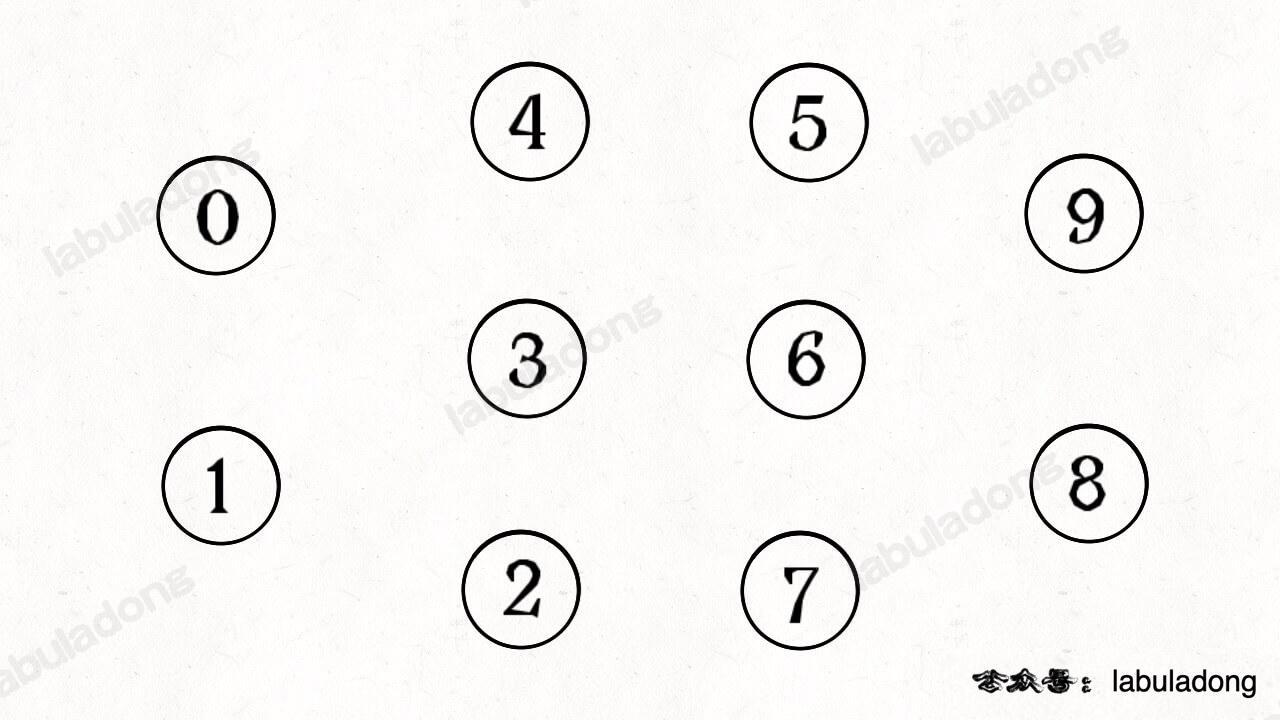
Simply put, dynamic connectivity can be seen as connecting nodes in a graph. For example, in the graph below, there are 10 nodes. They are not connected to each other, and are labeled from 0 to 9:

Our Union-Find algorithm mainly needs to implement these two APIs:

class UF {
    // connect p and q
    public void union(int p, int q);
    // determine if p and q are connected
    public boolean connected(int p, int q);
    // return the number of connected components in the graph
    public int count();
}

class UF {
public:
    // connect p and q
    void union_(int p, int q) = 0;

    // determine if p and q are connected
    bool connected(int p, int q) = 0;

    // return the number of connected components in the graph
    int count() = 0;
};

class UF:
    # connect p and q
    def union(self, p, q):
        pass
    
    # determine if p and q are connected
    def connected(self, p, q):
        pass

    # return the number of connected components in the graph
    def count(self):
        pass

type UF struct{}
// connect p and q
func (uf *UF) Union(p int, q int) {}
// determine if p and q are connected
func (uf *UF) Connected(p int, q int) bool {
   return false
}
// return the number of connected components in the graph
func (uf *UF) Count() int {
   return 0
}

var UF = function() {
    // connect p and q
    this.union = function(p, q) {}; 

    // determine if p and q are connected
    this.connected = function(p, q) {};

    // return the number of connected components in the graph
    this.count = function() {};
};

The "connected" relation here is an equivalence relation. It has these three properties:

1. Reflexive: node p is connected to itself p.

2. Symmetric: if node p is connected to q, then q is also connected to p.

3. Transitive: if node p is connected to q, and q is connected to r, then p is connected to r.

For example, in the graph above, any two different nodes from 0 to 9 are not connected. Calling connected on any pair returns false, and there are 10 connected components.

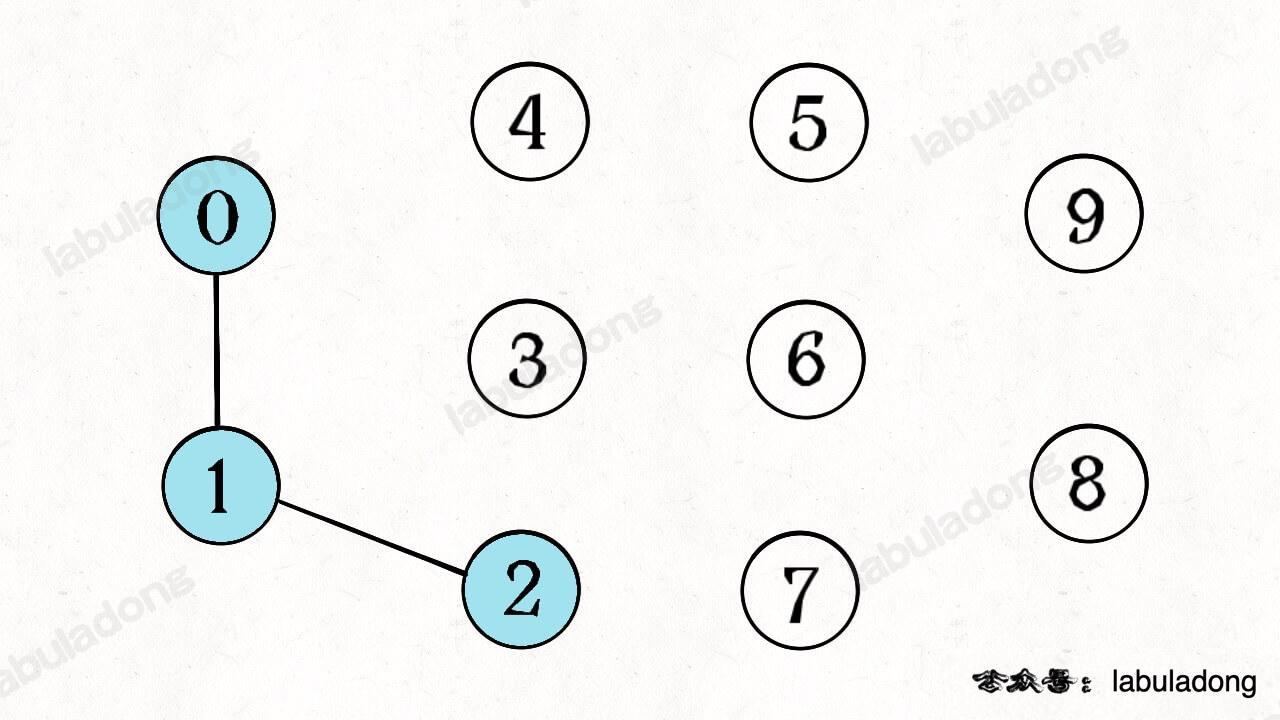
If we call union(0, 1), then 0 and 1 become connected, and the number of connected components drops to 9.

Then we call union(1, 2). Now 0, 1, 2 are all connected. Calling connected(0, 2) will return true, and the number of connected components becomes 8.

Checking this kind of equivalence relation is very useful, like when a compiler checks different references to the same variable, or when social networks compute friend circles, and so on.

Now you should have a basic idea of what dynamic connectivity is. The key of the Union-Find algorithm is the efficiency of the union and connected functions. So, what model should we use to represent the connectivity of this graph? What data structure should we use to implement the code?

2. Basic Idea

3. Balance Optimization

4. Path Compression