Key Points to Implement Linear Probing

labuladongOriginalAbout 2392 words

Prerequisite Knowledge

Before reading this article, you need to learn:

Core Principles of Hash Tables

In the previous article Core Principles of Hash Tables, I introduced the core principles and key concepts of hash tables. It mentioned that there are mainly two methods to resolve hash collisions: chaining and linear probing (also known as open addressing):

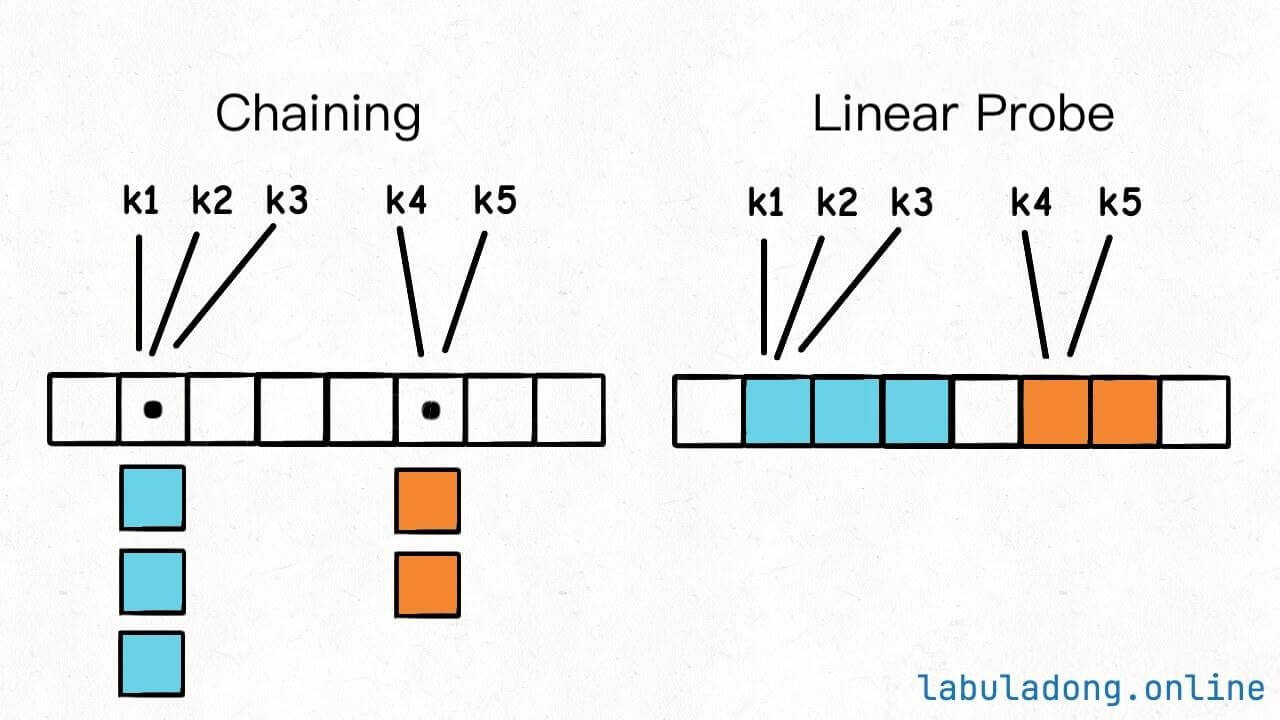
Since linear probing is a bit more complex, this article will first explain several challenges in implementing linear probing, and the next article will provide the actual code implementation.

Simplified Scenario

The previously introduced chaining method is relatively straightforward, where each element in the table is a linked list, and when a hash collision occurs, you simply insert the element into the list.

Linear probing is more complex, primarily due to two challenges that involve various array operation techniques. Before clarifying these challenges, let's establish a simplified scenario:

Assume our hash table only supports key and value types as int, with a fixed table.length of 10, and the hash function implemented as hash(key) = key % 10. This setup easily simulates hash collisions, such as both hash(1) and hash(11) resulting in 1.

The general logic of linear probing is as follows:

java 🟢

// The basic logic of linear probing, pseudocode implementation

class MyLinearProbingHashMap {
    // Each element in the array stores a key-value pair
    private KVNode[] table = new KVNode[10];

    private int hash(int key) {
        return key % table.length;
    }

    public void put(int key, int value) {
        int index = hash(key);
        KVNode node = table[index];
        if (node == null) {
            table[index] = new KVNode(key, value);
        } else {
            // Logic of linear probing
            // Probe backwards until the key is found or an empty slot is found
            while (index < table.length && table[index] != null && table[index].key != key) {
                index++;
            }
            table[index] = new KVNode(key, value);
        }
    }

    public int get(int key) {
        int index = hash(key);
        // Probe backwards until the key is found or an empty slot is found
        while (index < table.length && table[index] != null && table[index].key != key) {
            index++;
        }
        if (table[index] == null) {
            return -1;
        }
        return table[index].value;
    }

    public void remove(int key) {
        int index = hash(key);
        // Probe backwards until the key is found or an empty slot is found
        while (index < table.length && table[index] != null && table[index].key != key) {
            index++;
        }
        // Remove table[index]
        // ...
    }
}

cpp 🤖

// The basic logic of linear probing, pseudo-code implementation

class KVNode {
public:
    int key;
    int value;
    KVNode(int k, int v) : key(k), value(v) {}
};

class MyLinearProbingHashMap {
private:
    // Each element in the array stores a key-value pair
    KVNode* table[10] = {nullptr};

    int hash(int key) {
        return key % 10;
    }

public:
    // Destructor
    ~MyLinearProbingHashMap() {
        for (int i = 0; i < 10; i++) {
            if (table[i] != nullptr) {
                delete table[i];
                table[i] = nullptr;
            }
        }
    }

    void put(int key, int value) {
        int index = hash(key);
        KVNode* node = table[index];
        if (node == nullptr) {
            table[index] = new KVNode(key, value);
        } else {
            // The logic of linear probing
            // Probe backwards until the key is found or an empty slot is found
            while (index < 10 && table[index] != nullptr && table[index]->key != key) {
                index++;
            }
            delete table[index];
            table[index] = new KVNode(key, value);
        }
    }

    int get(int key) {
        int index = hash(key);
        // Probe backwards until the key is found or an empty slot is found
        while (index < 10 && table[index] != nullptr && table[index]->key != key) {
            index++;
        }
        if (index >= 10 || table[index] == nullptr) {
            return -1;
        }
        return table[index]->value;
    }

    void remove(int key) {
        int index = hash(key);
        // Probe backwards until the key is found or an empty slot is found
        while (index < 10 && table[index] != nullptr && table[index]->key != key) {
            index++;
        }
        // Delete table[index]
        // ...
    }
};

python 🤖

# Basic logic of linear probing, pseudo-code implementation

class KVNode:
    def __init__(self, key, value):
        self.key = key
        self.value = value

class MyLinearProbingHashMap:
    # Each element in the array stores a key-value pair
    def __init__(self):
        self.table = [None] * 10
    
    def hash(self, key):
        return key % len(self.table)

    def put(self, key, value):
        index = self.hash(key)
        node = self.table[index]
        if node is None:
            self.table[index] = KVNode(key, value)
        else:
            # Logic of linear probing
            # Probe backwards until key is found or an empty slot is found
            while index < len(self.table) and self.table[index] is not None and self.table[index].key != key:
                index += 1
            self.table[index] = KVNode(key, value)
    
    def get(self, key):
        index = self.hash(key)
        # Probe backwards until key is found or an empty slot is found
        while index < len(self.table) and self.table[index] is not None and self.table[index].key != key:
            index += 1
        if self.table[index] is None:
            return -1
        return self.table[index].value
    
    def remove(self, key):
        index = self.hash(key)
        # Probe backwards until key is found or an empty slot is found
        while index < len(self.table) and self.table[index] is not None and self.table[index].key != key:
            index += 1
        # Delete table[index]
        # ...

go 🤖

// Basic logic of linear probing, pseudo-code implementation

// Each element in the array stores a key-value pair
type KVNode struct {
	key   int
	value int
}

type MyLinearProbingHashMap struct {
	table []*KVNode
}

func NewMyLinearProbingHashMap() *MyLinearProbingHashMap {
	return &MyLinearProbingHashMap{
		table: make([]*KVNode, 10),
	}
}

func (m *MyLinearProbingHashMap) hash(key int) int {
	return key % len(m.table)
}

func (m *MyLinearProbingHashMap) Put(key int, value int) {
	index := m.hash(key)
	node := m.table[index]
	if node == nil {
		m.table[index] = &KVNode{key: key, value: value}
	} else {
		// Logic of linear probing
		// Probe backwards until you find the key or an empty slot
		for index < len(m.table) && m.table[index] != nil && m.table[index].key != key {
			index++
		}
		m.table[index] = &KVNode{key: key, value: value}
	}
}

func (m *MyLinearProbingHashMap) Get(key int) int {
	index := m.hash(key)
	// Probe backwards until you find the key or an empty slot
	for index < len(m.table) && m.table[index] != nil && m.table[index].key != key {
		index++
	}
	if m.table[index] == nil {
		return -1
	}
	return m.table[index].value
}

func (m *MyLinearProbingHashMap) Remove(key int) {
	index := m.hash(key)
	// Probe backwards until you find the key or an empty slot
	for index < len(m.table) && m.table[index] != nil && m.table[index].key != key {
		index++
	}
	// Delete table[index]
    // ...
}

func main() {
	hashMap := NewMyLinearProbingHashMap()
	hashMap.Put(1, 10)
	hashMap.Put(2, 20)
	fmt.Println(hashMap.Get(1)) // 10
	fmt.Println(hashMap.Get(2)) // 20
	fmt.Println(hashMap.Get(3)) // -1

	hashMap.Put(2, 30)
	fmt.Println(hashMap.Get(2)) // 30

	hashMap.Remove(2)
	fmt.Println(hashMap.Get(2)) // -1
}

javascript 🤖

// basic logic of linear probing method, pseudo-code implementation
class MyLinearProbingHashMap {
    constructor() {
        // each element in the array stores a key-value pair
        this.table = new Array(10).fill(null);
    }

    hash(key) {
        return key % this.table.length;
    }

    put(key, value) {
        var index = this.hash(key);
        var node = this.table[index];
        if (node === null) {
            this.table[index] = { key: key, value: value };
        } else {
            // logic of linear probing method
            // probe backwards until a key is found or an empty slot is found
            while (index < this.table.length && this.table[index] !== null && this.table[index].key !== key) {
                index++;
            }
            this.table[index] = { key: key, value: value };
        }
    }

    get(key) {
        var index = this.hash(key);
        // probe backwards until a key is found or an empty slot is found
        while (index < this.table.length && this.table[index] !== null && this.table[index].key !== key) {
            index++;
        }
        if (this.table[index] === null) {
            return -1;
        }
        return this.table[index].value;
    }

    remove(key) {
        var index = this.hash(key);
        // probe backwards until a key is found or an empty slot is found
        while (index < this.table.length && this.table[index] !== null && this.table[index].key !== key) {
            index++;
        }
        // delete this.table[index]
        // ...
    }
}

Based on this hypothetical scenario, let's examine the two challenges of linear probing.

Key Points to Implement Linear Probing

Simplified Scenario

Difficulty 1: The Need for Circular Array Techniques

Challenge Two: Complex Deletion Operation

Method 1: Data Shifting to Avoid Gaps

Method 2: Placeholder Marking for Deletion

Summary