球盒模型:回溯算法穷举的两种视角
本文讲解的例题
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 46. Permutations | 46. 全排列 | 🟠 |
| 78. Subsets | 78. 子集 | 🟠 |
阅读本文之前,需要你熟悉 回溯算法核心框架 以及 回溯算法秒杀所有排列/组合/子集问题。
在上面这两篇文章中,有读者提出了不同的排列/组合/子集代码写法,比如通过 swap 元素实现全排列,还有没有 for 循环的子集解法代码。我之前不提这些不同的解法,是为了保持这些问题解法形式的一致性,如果在一开始就给大家太多选择,反而容易让人迷糊。
在这篇文章,我不仅会具体介绍之前没有讲到的回溯算法写法,还会告诉你为什么可以那样写,两种写法的本质区别是什么。
先说结论
1、回溯算法穷举的本质思维模式是「球盒模型」,一切回溯算法,皆从此出,别无二法。
2、球盒模型,必然有两种穷举视角,分别为「球」的视角穷举和「盒」的视角穷举,对应的,就是两种不同的代码写法。
3、从理论上分析,两种穷举视角本质上是一样的。但是涉及到具体的代码实现,两种写法的复杂度可能有优劣之分。你需要选择效率更高的写法。
球盒模型这个词是我随口编的,因为下面我会用「球」和「盒」两种视角来解释,你理解就好。
暴力穷举思维方法:球盒模型
一切暴力穷举算法,都从球盒模型开始,没有例外。
你懂了这个,就可以随心所欲运用暴力穷举算法,下面的内容,请你仔细看,认真想。
首先,我们回顾一下以前学过的排列组合知识:
1、P(n, k)(也有很多书写成 A(n, k))表示从 n 个不同元素中拿出 k 个元素的排列(Permutation/Arrangement)总数;C(n, k) 表示从 n 个不同元素中拿出 k 个元素的组合(Combination)总数。
2、「排列」和「组合」的主要区别在于是否考虑顺序的差异。
3、排列、组合总数的计算公式:
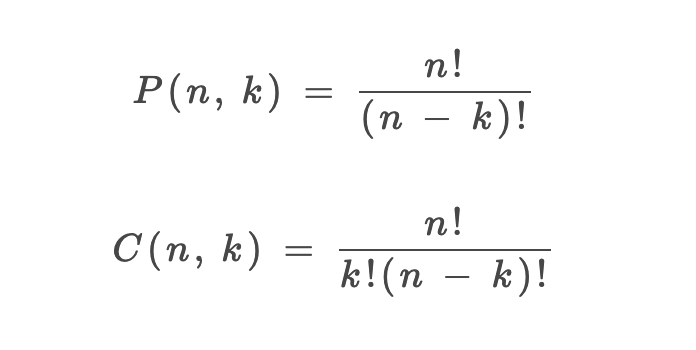
排列 P(n, k)
好,现在我问一个问题,这个排列公式 P(n, k) 是如何推导出来的?为了搞清楚这个问题,我需要讲一点组合数学的知识。
排列组合问题的各种变体都可以抽象成「球盒模型」,P(n, k) 就可以抽象成下面这个场景:
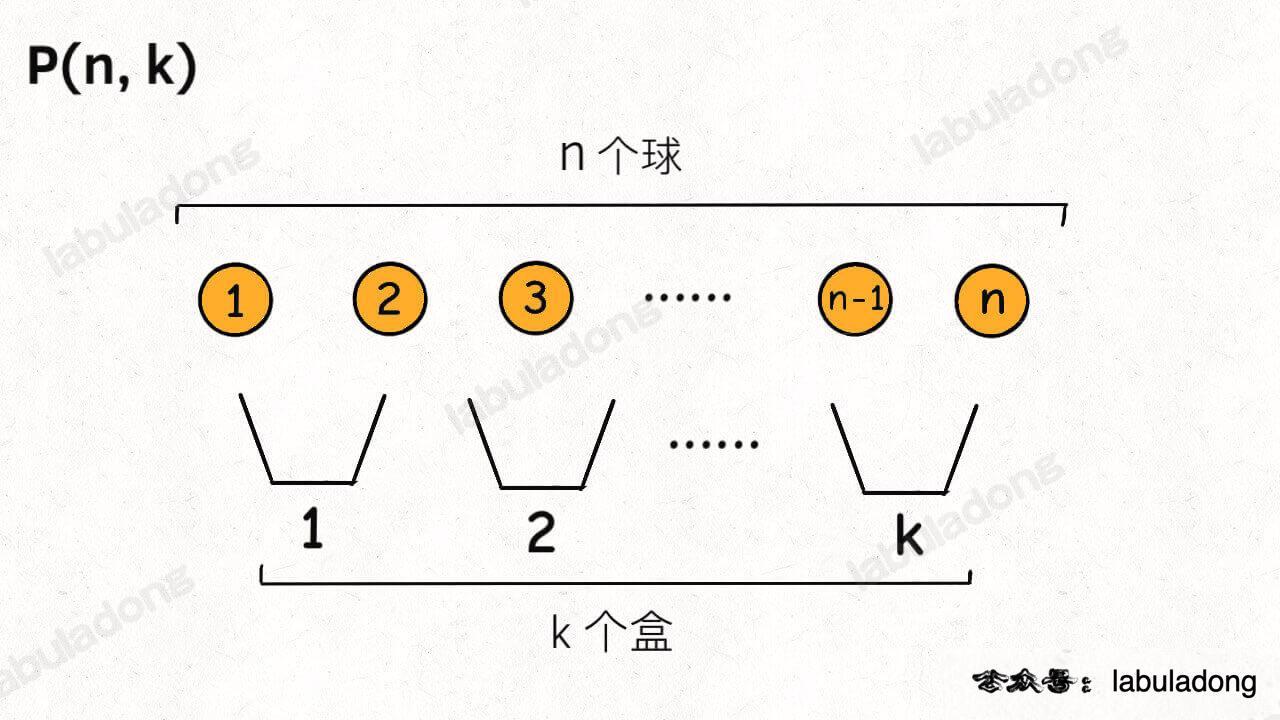
即,将 n 个标记了不同序号的球(标号为了体现顺序的差异),放入 k 个标记了不同序号的盒子中(其中 n >= k,每个盒子最终都装有恰好一个球),共有 P(n, k) 种不同的方法。
现在你来,往盒子里放球,你怎么放?其实有两种视角。
首先,你可以站在盒子的视角,每个盒子必然要选择一个球。
这样,第一个盒子可以选择 n 个球中的任意一个,然后你需要让剩下 k - 1 个盒子在 n - 1 个球中选择(这就是子问题 P(n - 1, k - 1)):
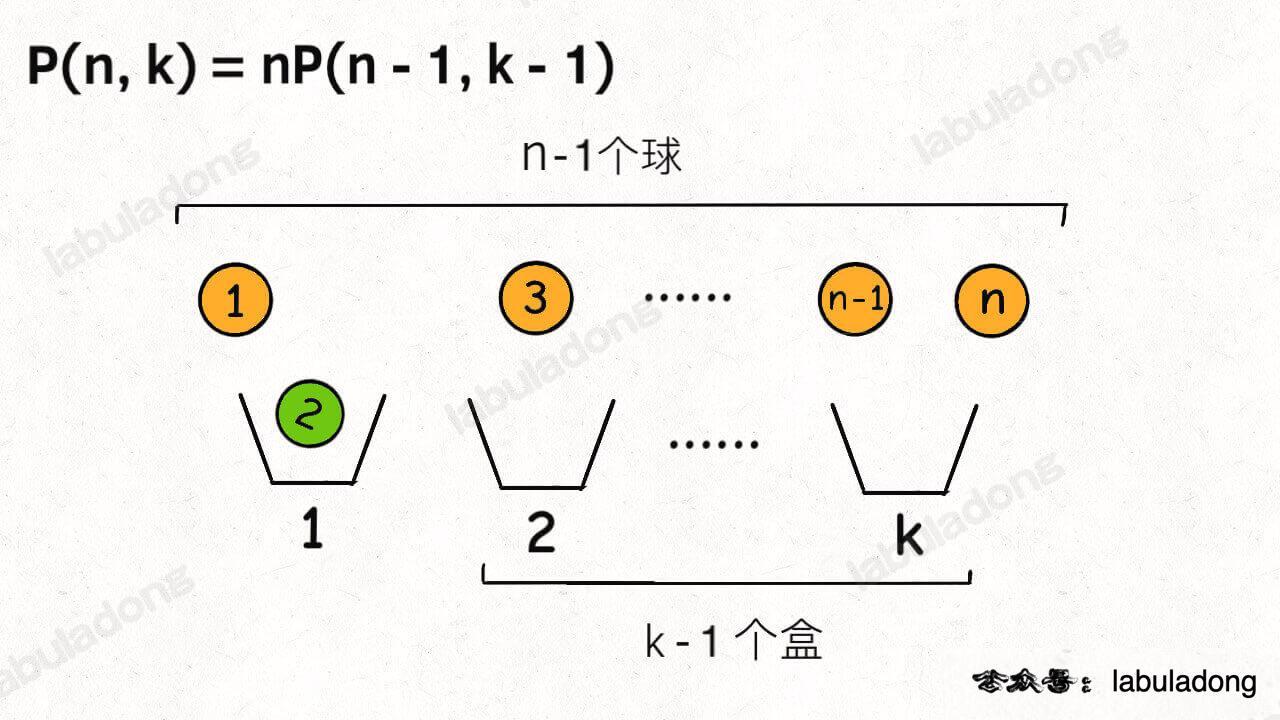
另外,你也可以站在球的视角,因为并不是每个球都会被装进盒子,所以球的视角分两种情况:
1、第一个球可以不装进任何一个盒子,这样的话你就需要将剩下 n - 1 个球放入 k 个盒子。
2、第一个球可以装进 k 个盒子中的任意一个,这样的话你就需要将剩下 n - 1 个球放入 k - 1 个盒子。
结合上述两种情况,可以得到:
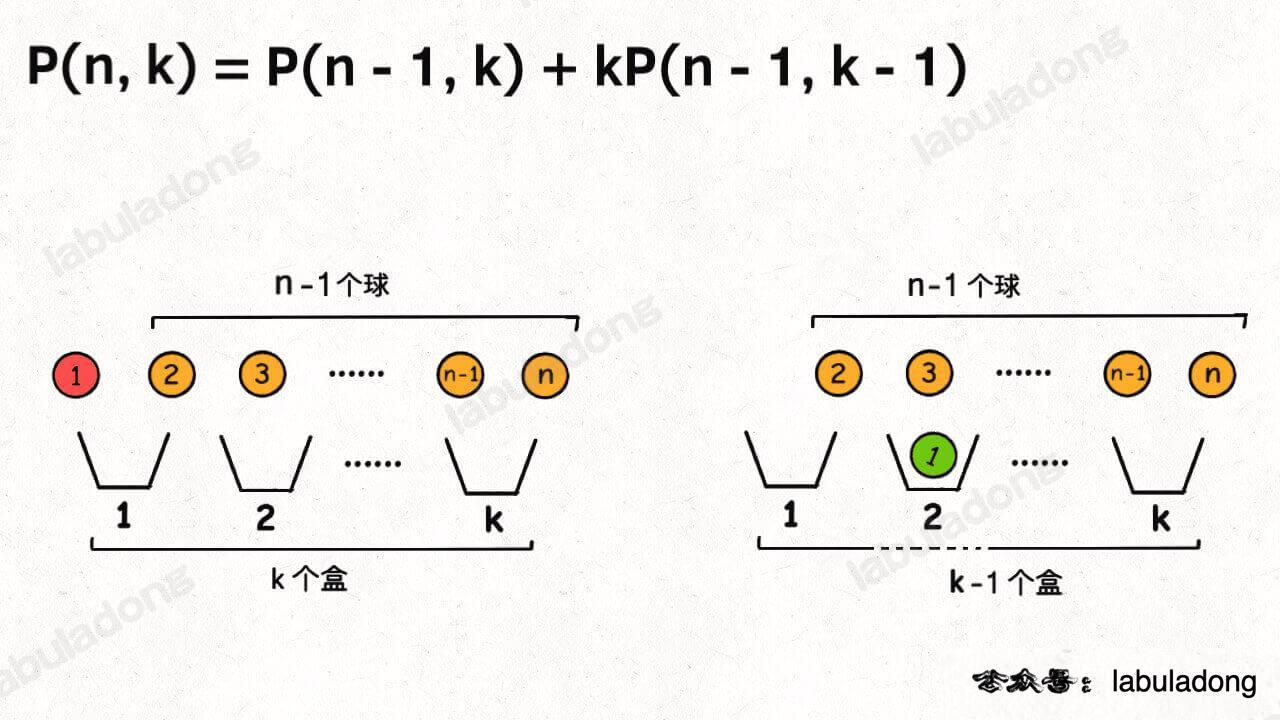
你看,两种视角得到两个不同的递归式,但这两个递归式解开的结果都是我们熟知的阶乘形式:
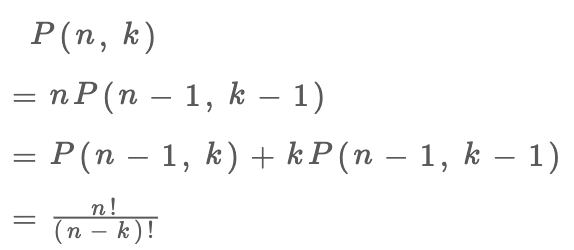
至于如何解递归式,涉及数学的内容比较多,这里就不做深入探讨了,有兴趣的读者可以自行学习组合数学相关知识。