回溯算法实践:数独和 N 皇后问题
本文讲解的例题
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 37. Sudoku Solver | 37. 解数独 | 🔴 |
| 51. N-Queens | 51. N 皇后 | 🔴 |
| 52. N-Queens II | 52. N皇后 II | 🔴 |
你已经学习过 回溯算法核心框架,那么本文就来探讨两道经典算法题:数独游戏和 N 皇后问题。
选择这两个问题,主要是它们的解法思路非常相似,而且它们都是回溯算法在实际生活中的有趣应用。
游戏简介
数独游戏
大家应该都玩过数独游戏,就是给你一个 9x9 的棋盘,其中有一些格子预先填入了数字,让你在其余空的格子中填入数字 1~9,要求每行、每列和每个 3x3 的九宫格内数字都不能重复。
下面是一个数独游戏的例子(来源 Wikipedia):

我小的时候也尝试过玩数独游戏,但只要稍微有些难度,就搞不定了。后来我才知道做数独是有技巧的,有一些比较专业的数独游戏软件会教你玩数独的技巧,不过在我看来这些技巧都太复杂,根本就没有兴趣看下去。
现在学习了回溯算法,多困难的数独问题都拦不住我了。只要有规则,就一定可以暴力穷举出符合条件的答案来,不是吗?
下面是我用回溯算法完成数独的例子:

稍后我会详细讲解这道题的解法。
N 皇后问题
在国际象棋中,皇后可以攻击同一行、同一列和同一条对角线上的任意单位。N 皇后问题是指在一个 N×N 的棋盘上摆放 N 个皇后,要求任何两个皇后之间都不能互相攻击。
换句话说,就是让你在一个 N×N 的棋盘上放置 N 个皇后,使得每行、每列和每个对角线都只有一个皇后。
比如这是 8 皇后问题的一个解(来源 Wikipedia):
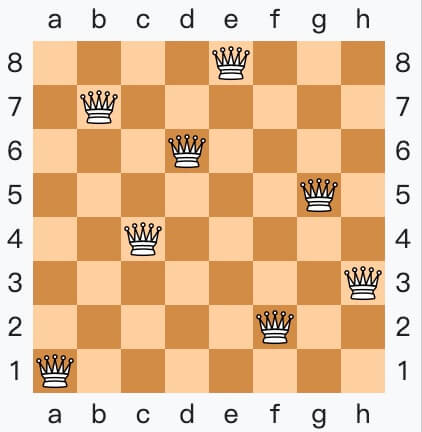
可以看到,对于任意一个皇后,它所在的行、列和对角线(左上、右上、左下、右下)都没有其他皇后,所以这就是一个符合规则的解。
在讲上述题目之前,我需要先讲一道比较简单的回溯算法问题,把这个问题作为铺垫,就能更容易理解数独游戏和 N 皇后问题的解法了。
n 位二进制数的所有可能
我来给你编一道简单的题目,请你实现这样一个函数:
List<String> generateBinaryNumber(int n);vector<string> generateBinaryNumber(int n);def generateBinaryNumber(n: int) -> List[str]:func generateBinaryNumber(n int) []string {}var generateBinaryNumber = function(n) {};函数的输入是一个正整数 n,请你返回所有长度为 n 的二进制数(0、1 组成),你可以按任意顺序返回答案。
比如说 n = 3,那么你需要以字符串形式返回如下 种不同的二进制数:
000
001
010
011
100
101
110
111这道题可以认为是数独游戏和 N 皇后问题的简化版:
这道题相当于让你对一个长度为 n 的一维数组中的每一个位置进行穷举,其中每个位置可以填 0 或 1。
数独游戏相当于让你对一个 9x9 的二维数组中的每个位置进行穷举,其中每个位置可以是数字 1~9,且同一行、同一列和同一个 3x3 的九宫格内数字不能重复。
N 皇后问题相当于让你对一个 N x N 的二维数组中的每个位置进行穷举,其中每个位置可以不放皇后或者放置皇后(相当于 0 或 1),且不能存在多个皇后在同一行、同一列或同一对角线上。
所以,只要你把这道简化版的题目的穷举过程搞明白,其他问题都迎刃而解了,无非是规则多了一些而已。