拓展：快速排序详解及应用

前文 归并排序算法详解 通过二叉树的视角描述了归并排序的算法原理以及应用，很多读者大呼精妙，那我就趁热打铁，今天继续用二叉树的视角讲一讲快速排序算法的原理以及运用。

快速排序算法思路

首先我们看一下快速排序的代码框架：

void sort(int[] nums, int lo, int hi) {
    if (lo >= hi) {
        return;
    }
    // 对 nums[lo..hi] 进行切分
    // 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]
    int p = partition(nums, lo, hi);
    // 去左右子数组进行切分
    sort(nums, lo, p - 1);
    sort(nums, p + 1, hi);
}

void sort(int nums[], int lo, int hi) {
    if (lo >= hi) {
        return;
    }
    // 对 nums[lo..hi] 进行切分
    // 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]
    int p = partition(nums, lo, hi);
    // 去左右子数组进行切分
    sort(nums, lo, p - 1);
    sort(nums, p + 1, hi);
}

def sort(nums: List[int], lo: int, hi: int):
    if lo >= hi:
        return
    # 对 nums[lo..hi] 进行切分
    # 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]
    p = partition(nums, lo, hi)
    # 去左右子数组进行切分
    sort(nums, lo, p - 1)
    sort(nums, p + 1, hi)

func sort(nums []int, lo int, hi int) {
    if lo >= hi {
        return
    }
    // 对 nums[lo..hi] 进行切分
    // 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]
    p := partition(nums, lo, hi)
    // 去左右子数组进行切分
    sort(nums, lo, p-1)
    sort(nums, p+1, hi)
}

var sort = function(nums, lo, hi) {
    if (lo >= hi) {
        return;
    }
    // 对 nums[lo..hi] 进行切分
    // 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]
    var p = partition(nums, lo, hi);
    // 去左右子数组进行切分
    sort(nums, lo, p - 1);
    sort(nums, p + 1, hi);
};

其实你对比之后可以发现，快速排序就是一个二叉树的前序遍历：

// 二叉树遍历框架
void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    // ***** 前序位置 *****
    print(root.val);
    // *******************
    traverse(root.left);
    traverse(root.right);
}

// 二叉树遍历框架
void traverse(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    // ***** 前序位置 *****
    cout << root->val << endl;
    // *******************
    traverse(root->left);
    traverse(root->right);
}

# 二叉树遍历框架
def traverse(root: TreeNode):
    if not root:
        return
    # 前序位置
    print(root.val)
    traverse(root.left)
    traverse(root.right)

// 二叉树遍历框架
func traverse(root *TreeNode) {
    if root == nil {
        return
    }
    // 前序位置
    fmt.Println(root.Val)
    traverse(root.Left)
    traverse(root.Right)
}

// 二叉树遍历框架
var traverse = function(root) {
    if (root === null) {
        return;
    }
    // ***** 前序位置 *****
    console.log(root.val);
    // *******************
    traverse(root.left);
    traverse(root.right);
};

另外，前文 归并排序详解 用一句话总结了归并排序：先把左半边数组排好序，再把右半边数组排好序，然后把两半数组合并。

同时我提了一个问题，让你一句话总结快速排序，这里说一下我的答案：

快速排序是先将一个元素排好序，然后再将剩下的元素排好序。

为什么这么说呢，且听我慢慢道来。

快速排序的核心无疑是 partition 函数， partition 函数的作用是在 nums[lo..hi] 中寻找一个切分点 p，通过交换元素使得 nums[lo..p-1] 都小于等于 nums[p]，且 nums[p+1..hi] 都大于 nums[p]：

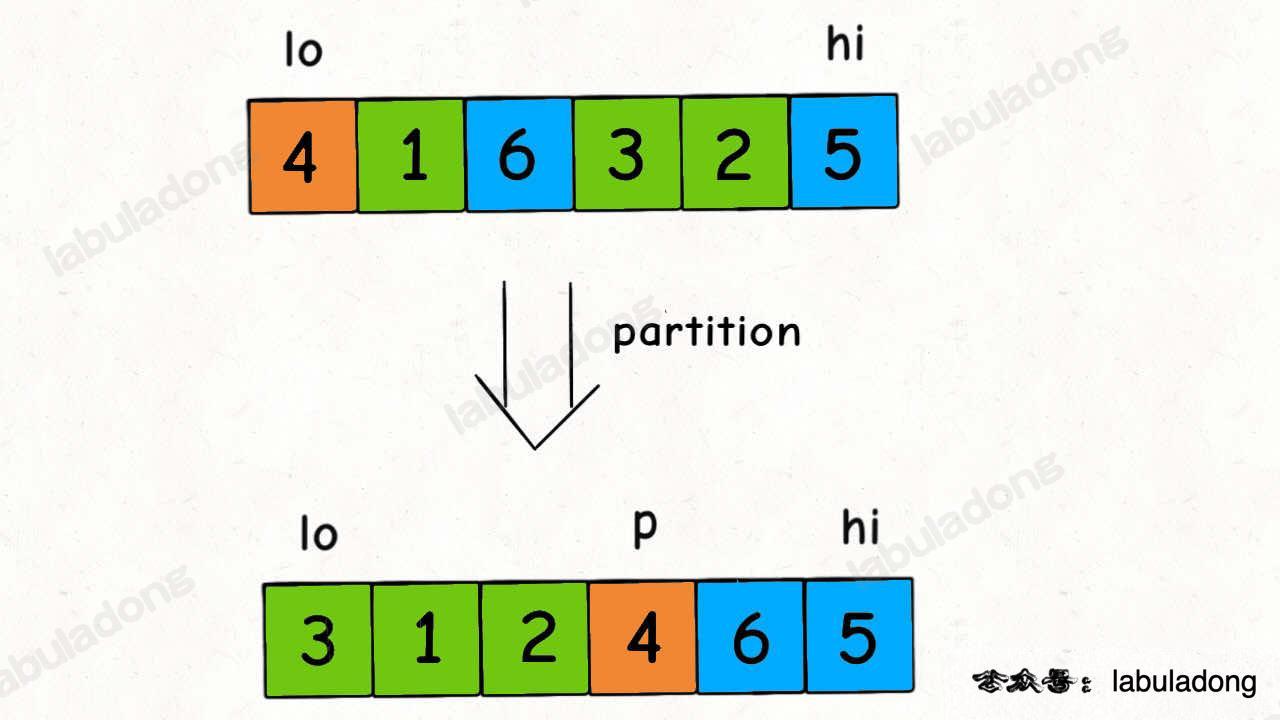
一个元素左边的元素都比它小，右边的元素都比它大，啥意思？不就是它自己已经被放到正确的位置上了吗？

所以 partition 函数干的事情，其实就是把 nums[p] 这个元素排好序了。

一个元素被排好序了，然后呢？你再把剩下的元素排好序不就得了。

剩下的元素有哪些？左边一坨，右边一坨，去吧，对子数组进行递归，用 partition 函数把剩下的元素也排好序。

从二叉树的视角，我们可以把子数组 nums[lo..hi] 理解成二叉树节点上的值，sort 函数理解成二叉树的遍历函数。

参照二叉树的前序遍历顺序，快速排序的运行过程如下 GIF：