二维数组的花式遍历技巧
本文讲解的例题
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 151. Reverse Words in a String | 151. 反转字符串中的单词 | 🟠 |
| 48. Rotate Image | 48. 旋转图像 | 🟠 |
| 54. Spiral Matrix | 54. 螺旋矩阵 | 🟠 |
| 59. Spiral Matrix II | 59. 螺旋矩阵 II | 🟠 |
| 61. Rotate List | 61. 旋转链表 | 🟠 |
| - | 剑指 Offer 29. 顺时针打印矩阵 | 🟢 |
有些读者说,看了本站的很多文章,掌握了框架思维,可以解决大部分有套路框架可循的题目。
但是框架思维也不是万能的,有一些特定技巧呢,属于会者不难,难者不会的类型,只能通过多刷题进行总结和积累。
那么本文我分享一些巧妙的二维数组的花式操作,你只要有个印象,以后遇到类似题目就不会懵圈了。
顺/逆时针旋转矩阵
对二维数组进行旋转是常见的笔试题,力扣第 48 题「旋转图像」就是很经典的一道:
48. 旋转图像 | 力扣 | LeetCode | 🟠
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
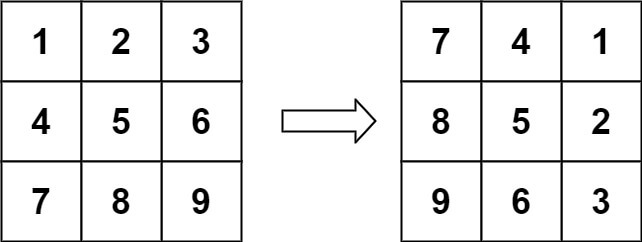
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[[7,4,1],[8,5,2],[9,6,3]]
示例 2:
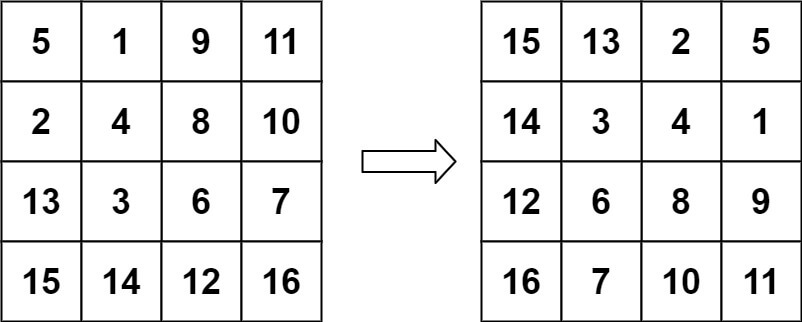
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
提示:
n == matrix.length == matrix[i].length1 <= n <= 20-1000 <= matrix[i][j] <= 1000
题目很好理解,就是让你将一个二维矩阵顺时针旋转 90 度,难点在于要「原地」修改,函数签名如下:
void rotate(int[][] matrix)void rotate(vector<vector<int>>& matrix)def rotate(matrix: List[List[int]]) -> None:func rotate(matrix [][]int) {}var rotate = function(matrix) {}如何「原地」旋转二维矩阵?稍想一下,感觉操作起来非常复杂,可能要设置巧妙的算法机制来「一圈一圈」旋转矩阵:
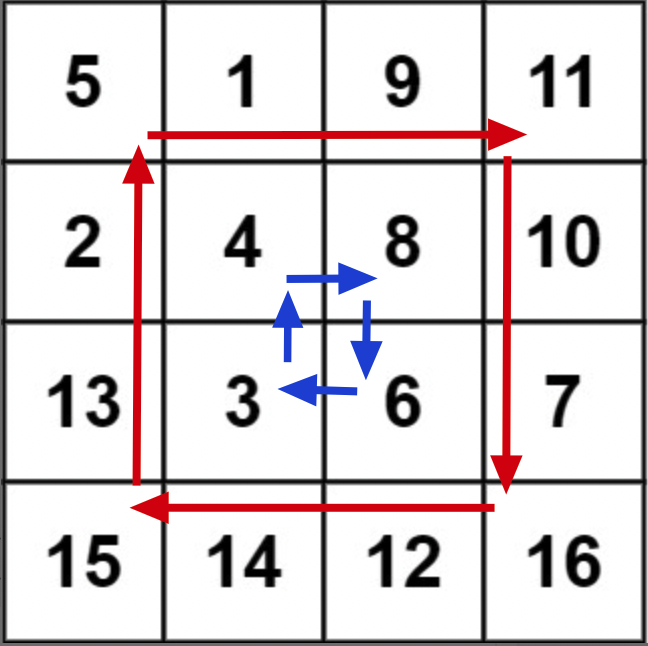
但实际上,这道题不能走寻常路,在讲巧妙解法之前,我们先看另一道谷歌曾经考过的算法题热热身:
给你一个包含若干单词和空格的字符串 s,请你写一个算法,原地反转所有单词的顺序。
比如说,给你输入这样一个字符串:
s = "hello world labuladong"你的算法需要原地反转这个字符串中的单词顺序:
s = "labuladong world hello"常规的方式是把 s 按空格 split 成若干单词,然后 reverse 这些单词的顺序,最后把这些单词 join 成句子。但这种方式使用了额外的空间,并不是「原地反转」单词。
正确的做法是,先将整个字符串 s 反转:
s = "gnodalubal dlrow olleh"然后将每个单词分别反转:
s = "labuladong world hello"这样,就实现了原地反转所有单词顺序的目的。力扣第 151 题「颠倒字符串中的单词」就是类似的问题,你可以顺便去做一下。
上面这个小技巧还可以再包装包装,比如说你可以去看一下力扣第 61 题「旋转链表」:给你一个单链表,让你旋转链表,将链表每个节点向右移动 k 个位置。
比如说输入单链表 1 -> 2 -> 3 -> 4 -> 5,k = 2,你的算法需要返回 4 -> 5 -> 1 -> 2 -> 3,即将链表每个节点向右移动 2 个位置。
这个题,不要真傻乎乎地一个一个去移动链表节点,我给你翻译翻译,其实就是将链表的后 k 个节点移动到链表的头部嘛,反应过来没有?
还没反应过来,那再提示一下,把后 k 个节点移动到链表的头部,其实就是让你把链表的前 n - k 个节点和后 k 个节点原地翻转,对不对?
这样,是不是和前面说的原地翻转字符串中的单词是一样的道理呢?你只需要先将整个链表反转,然后将前 n - k 个节点和后 k 个节点分别反转,就得到了结果。
当然,这个题有一些小细节,比如这个 k 可能大于链表的长度,那么你需要先求出链表的长度 n,然后取模 k = k % n,这样 k 就不会大于链表的长度,且最后得到的结果也是正确的。
有时间的话自己去做一下这个题吧,比较简单,我这里就不贴代码了。
我讲上面这两道题的目的是什么呢?
旨在说明,有时候咱们拍脑袋的常规思维,在计算机看来可能并不是最优雅的;但是计算机觉得最优雅的思维,对咱们来说却不那么直观。也许这就是算法的魅力所在吧。