算法可视化面板使用说明
写给初学/希望速成算法的读者
每道题的可视化代码我都提前写好了，甚至我会在文章或者注释中告诉你应该如何操作可视化面板来观察算法的执行过程。
所以对于初学者和希望速成的读者，了解本文第一部分「基本用法」中的内容就够用了。
写给进阶读者/算法爱好者
有些读者希望修改我的预设代码，或者对自己的一些奇思妙想进行可视化验证，那么就需要了解可视化面板的特殊能力，可以参考本文后半部分的内容。
可视化面板目前只支持 JavaScript 代码。如果你阅读可视化面板中的 JavaScript 代码有困难，我专门写了一个使用可视化面板的 极简 JavaScript 教程，帮助你 5 分钟上手。
可视化面板编辑器网页地址：
https://labuladong.online/algo-visualize/
另外，本站以及所有配套插件中嵌套的算法可视化面板也添加了「编辑」按钮，点击后即可直接修改并执行你的代码进行可视化。
基本用法
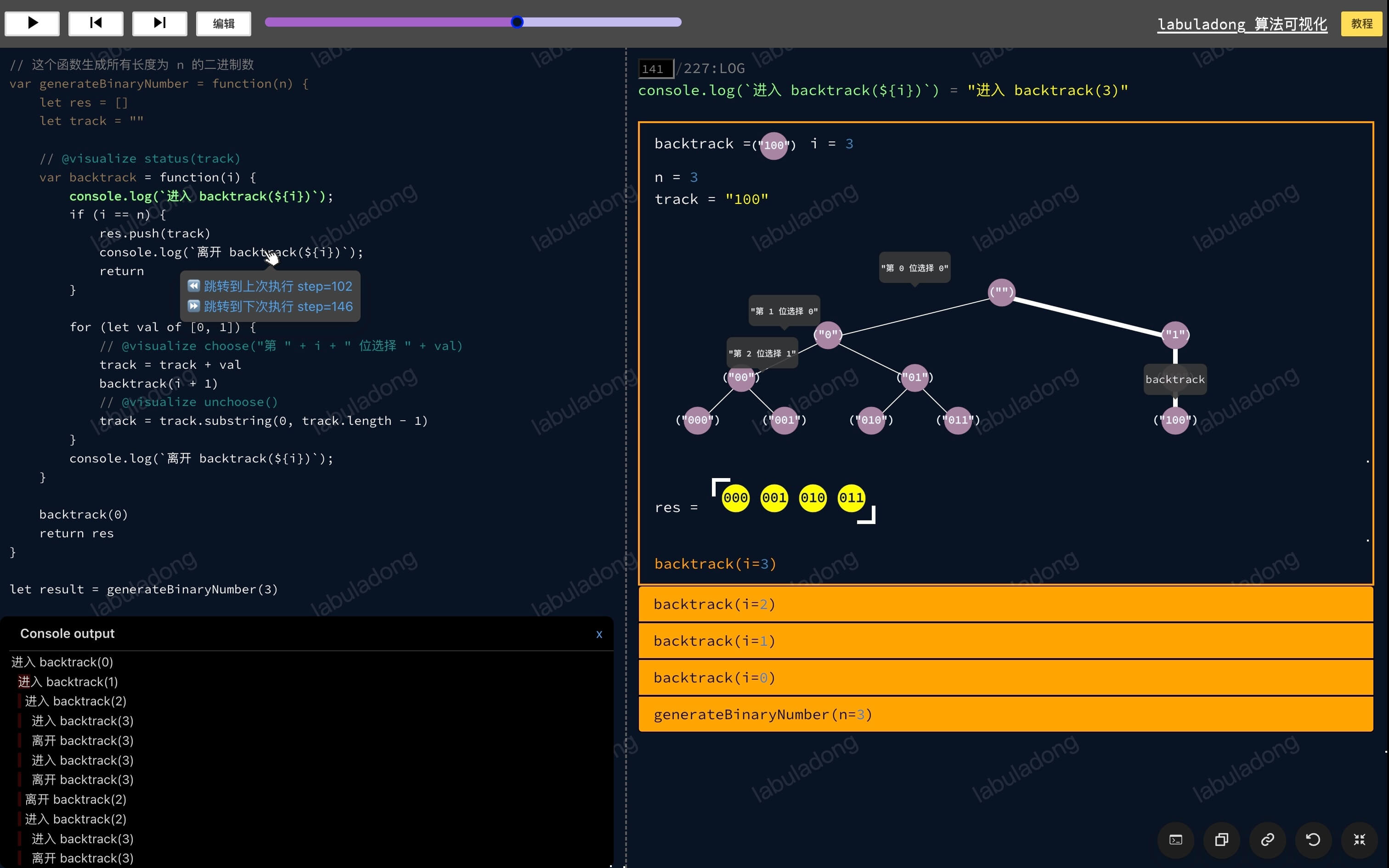
左侧是代码面板，当前执行到的代码行会高亮显示，点击代码可以直接运行到指定位置；鼠标悬浮到代码上可以跳转到上次执行或下次执行的位置。
最常用的技巧
点击代码运行到指定位置是最常用的，这个功能就和你在 IDE 中 debug 代码的那个「运行到光标位置」功能一样。
一般我们不会从头开始一步步播放算法的执行，而是直接点击代码跳转到某个感兴趣的位置，然后再一步步执行，观察算法的执行过程。
顶部主要是一些控制按钮和滑动条，可以精细控制代码逐步执行，编辑按钮允许你修改运行我预设的代码。
右侧是可视化区域，用来显示变量、数据结构、堆栈信息、递归树等等。鼠标悬浮到数据结构上可以查看详细信息。
左下角是 Log Console，如果你的代码中使用了 console.log，输出内容会被打印在这里。console.log 函数被我加强了，可以自动根据递归深度给输出内容加上缩进，方便你观察递归过程。
右下角有一些悬浮按钮，提供复制代码、刷新面板、全屏显示、显示/隐藏 Log Console 等功能。
了解这些就足够你玩转可视化面板了，你可以在这两个面板上玩一玩点一点，尝试一下这些功能。
初学者了解上面的内容就够用了。下面的内容介绍可视化面板的特殊功能，供有需要的读者参考。
数据结构的可视化
面板可以可视化数组、链表、二叉树、哈希表、哈希集合等常见数据结构，下面具体介绍一下如何创建这些数据结构。
标准库数据结构
类似数组、哈希表等 JavaScript 内置的数据结构，就正常初始化和操作它们即可，比如：
单链表
首先说一下单链表，单链表的每个节点有 val, next 属性，和力扣上的定义完全一致。
API 文档
// 单链表节点
abstract class ListNode {
val: any
next: ListNode | null
constructor(val: any, next: ListNode | null = null) {
this.val = val
this.next = next
}
}
abstract class LinkedList {
// 创建链表并返回头结点
static createHead(elems: any[]): ListNode {
}
// 创建带环的链表并返回头结点
static createCyclicHead(elems: any[], index: number): ListNode {
}
}双链表
双链表的每个节点有 val, prev, next 属性，构造函数和力扣完全一致。
API 文档
// 双链表节点
abstract class DListNode {
next: DListNode | null = null
prev: DListNode | null = null
val: any
constructor(val: any = 0, prev: DListNode = null, next: DListNode = null) {
this.val = val
this.prev = prev
this.next = next
}
}
// 双链表
abstract class DLinkedList {
// 创建双链表并返回头结点
static createHead(elems: any[]): DListNode {
}
}基于拉链法的哈希表
JavaScript 标准库提供了 Map 存储键值对，我这里提供的哈希表主要是为了配合 哈希表原理及实现 进行教学。
ChainingHashMap.create 方法可以创建一个基于拉链法的简化哈希表，仅支持存储整数键值对，不支持扩缩容。具体实现可以参考 拉链法实现哈希表。
API 文档
// 简化版的拉链法哈希表
abstract class ChainingHashMap {
// 创建一个拉链法哈希表，容量为 capacity
static create(capacity: number): ChainingHashMap {
}
// 添加或更新键值对
abstract put(key: number, value: number): void;
// 获取键值，如果不存在则返回 -1
abstract get(key: number): number;
// 删除键值对
abstract remove(key: number): void;
// 获取内部数组
abstract getTable(): Array<ListNode | null>;
// 获取指定索引处的链表头结点
abstract getTableIndex(index: number): ListNode | null;
}基于线性探查法的哈希表
和拉链法类似，基于线性探查法的哈希表也是为了配合 哈希表原理及实现 进行教学。
LinearProbingHashMap.create 方法可以创建一个基于线性探查法的简化哈希表，仅支持存储整数键值对，不支持扩缩容。具体实现可以参考 线性探查法实现哈希表。
API 文档
// 简化版的线性探测哈希表
abstract class LinearProbingHashMap {
// 创建一个线性探测哈希表，容量为 capacity
static create(capacity: number): LinearProbingHashMap {
}
// 添加或更新键值对
abstract put(key: number, value: number): void;
// 获取键值，如果不存在则返回 -1
abstract get(key: number): number;
// 删除键值对
abstract remove(key: number): void;
// 获取内部数组
abstract getTable(): Array<string | null>;
}二叉树
二叉树每个节点有 val, left, right 属性，构造函数和力扣保持一致。
你可以用 BTree.create 方法快速创建一棵二叉树。注意我们用列表来表示二叉树，表示方式和 力扣题目中表示二叉树的方式 相同。
API 文档
// 二叉树节点
abstract class TreeNode {
val: any
left: TreeNode | null
right: TreeNode | null
constructor(val: any, left: TreeNode | null = null, right: TreeNode | null = null) {
this.val = val
this.left = left
this.right = right
}
}
abstract class BTree {
// 按照力扣格式输入一个数组，返回一个二叉树的根节点
static createRoot(elems: any[]): TreeNode {
}
// 输入若干元素，构造一棵二叉搜索树，返回根节点
static createBSTRoot(elems: number[]): TreeNode {
}
}多叉树
多叉树的每个节点有 val, children 属性，构造函数和力扣完全一致。
API 文档
// N 叉树节点
abstract class NTreeNode {
val: any
children: NTreeNode[]
}
abstract class NTree {
// 输入一个数组，构造一棵 N 叉树
// 输入的格式参见力扣的这道题目：
// https://leetcode.cn/problems/n-ary-tree-level-order-traversal/
static create(items: any[]) {
}
}普通二叉搜索树
可以用 BSTMap.create 创建普通的二叉搜索树存储键值对，底层原理见 动手实现 TreeMap/TreeSet。
如果不需要存储键值对，可以用上面介绍的 BTree.createBSTRoot 基于标准的二叉树节点创建二叉搜索树。
API 文档
type compareFn = (a: any, b: any) => number
const defaultCompare = (a: any, b: any) => {
if (a === b) return 0
return a < b ? -1 : 1
}
abstract class BSTNode {
abstract key: any
abstract value: any
abstract left: null | BSTNode
abstract right: null | BSTNode
}
abstract class BSTMap {
static create(elems: any[] = [], compare: compareFn = defaultCompare): BSTMap {
}
abstract get(key: any): any
abstract containsKey(key: any): boolean
abstract put(key: any, value: any): void
abstract remove(key: any): void
abstract getMinKey(): any | null
abstract getMaxKey(): any | null
abstract keys(): any[]
abstract _getRoot(): BSTNode | null
}红黑二叉搜索树
可以用 RBTreeMap 类创建红黑二叉搜索树存储键值对，使用案例见 红黑树基础。
API 文档
type compareFn = (a: any, b: any) => number
const defaultCompare = (a: any, b: any) => {
if (a === b) return 0
return a < b ? -1 : 1
}
// 红黑树节点
abstract class RBTreeNode {
// 节点的颜色
static RED: string = '#b10000'
static BLACK: string = '#464546'
abstract key: any
abstract value: any
abstract color: string
abstract left: null | RBTreeNode
abstract right: null | RBTreeNode
static isRed(node: RBTreeNode): boolean {
if (!node) return false
return node.color === RBTreeNode.RED
}
}
abstract class RBTreeMap {
static create(elems: any[][] = [], compare: compareFn = defaultCompare): RBTreeMap {
}
abstract put(key: any, value: any): void
abstract get(key: any): any
abstract containsKey(key: any): boolean
abstract getMinKey(): any | null
abstract getMaxKey(): any | null
abstract deleteMinKey(): void
abstract deleteMaxKey(): void
abstract delete(key: any): void
abstract keys(): any[]
abstract _getRoot(): RBTreeNode | null
// 红黑树的一些关键方法
static makeNode(key: any, value: any, color: string): RBTreeNode {
}
static makeRedNode(key: any, value: any): RBTreeNode {
}
static makeBlackNode(key: any, value: any): RBTreeNode {
}
// 左旋操作
static rotateLeft(node: RBTreeNode): RBTreeNode {
}
static moveRedLeft(node: RBTreeNode): RBTreeNode {
}
// 右旋操作
static rotateRight(node: RBTreeNode): RBTreeNode {
}
static moveRedRight(node: RBTreeNode): RBTreeNode {
}
// 颜色翻转
static flipColors(node: RBTreeNode): void {
}
// 平衡操作
static balance(node: RBTreeNode): RBTreeNode {
}
}二叉堆（优先级队列）
我在 二叉堆基础及实现 中就结合可视化面板给大家讲解了二叉堆的基本概念、优先级队列的代码实现以及两个核心操作上浮 (swim) 和下沉 (sink) 的实现。同时，堆排序算法详解 中也用到了二叉堆的一些方法完成排序。
API 文档
type compareFn = (a: any, b: any) => number
const defaultCompare: compareFn = (a, b) => {
if (a < b) return -1;
if (a > b) return 1;
return 0;
};
// 二叉堆节点
abstract class HeapNode {
abstract val: any;
abstract left: HeapNode;
abstract right: HeapNode;
}
abstract class Heap {
// 创建一个堆，可以传入初始元素或者比较函数
static create(items: any[] = [], fn: compareFn = defaultCompare): Heap {
}
// 创建一个最大堆，可以传入初始元素
static createMax(items?: any[]): Heap {
}
// 创建一个最小堆，可以传入初始元素
static createMin(items?: any[]): Heap {
}
// 创建一个二叉堆节点
static makeNode(value: any): HeapNode {
}
// 向堆顶添加元素
abstract push(value: any): void;
// 弹出堆顶元素
abstract pop(): any;
// 查看堆顶元素
abstract peek(): any;
// 获取堆的元素个数
abstract size(): number;
// 显示堆底层的数组
abstract showArray(varName?: string): any[];
// 返回堆的根节点
// 主要用来讲解二叉堆原理
abstract _getRoot(): HeapNode | null;
// 将数组转换成完全二叉树，但不会自动应用堆的性质
// 主要用来讲解堆排序
static init(items: any[], fn: compareFn = defaultCompare) {
}
// 使节点上浮，维护二叉堆性质
// 主要用来讲解堆排序
static sink(heap: Heap, topIndex: number, size: number, compare: compareFn) {
}
// 使节点下沉，维护二叉堆性质
// 主要用来讲解堆排序
static swim(heap: Heap, index: number, compare: compareFn) {
}
}可视化面板默认使用二叉树的逻辑结构展示二叉堆，调用 showArray 方法可以同时显示二叉堆的底层数组结构。下面是一些使用示例：
线段树
SegementTree 类可以创建线段树，支持 query, update 等方法，底层原理见 线段树基础介绍。
目前内置了求和线段树、最大值线段树、最小值线段树，你可以直接调用 SegementTree.create 方法创建自定义线段树。
API 文档
type mergeFn = (a: any, b: any) => any
const sumMerger = (a: any, b: any) => a + b
const maxMerger = (a: any, b: any) => Math.max(a, b)
const minMerger = (a: any, b: any) => Math.min(a, b)
// 线段树节点
abstract class SegmentNode {
abstract val: any
abstract l: number
abstract r: number
abstract left: SegmentNode | null
abstract right: SegmentNode | null
}
// 线段树
abstract class SegmentTree {
// 创建自定义线段树
// merger 是一个函数，用来定义线段树的合并逻辑
// mergerName 是合并规则的名称，便于在可视化面板中的线段树节点显示
static create(items: any[], merger: mergeFn = sumMerger, mergerName: string = 'sum'): SegmentTree {
}
// 创建求和线段树，支持区间求和查询和单点更新
static createSum(items: any[]): SegmentTree {
return SegmentTree.create(items, sumMerger, 'sum')
}
// 创建最小值线段树，支持区间最小值查询和单点更新
static createMin(items: any[]): SegmentTree {
return SegmentTree.create(items, minMerger, 'min')
}
// 创建最大值线段树，支持区间最大值查询和单点更新
static createMax(items: any[]): SegmentTree {
return SegmentTree.create(items, maxMerger, 'max')
}
// 更新索引 index 的值为 value
abstract update(index: number, value: any): void
// 查询闭区间 [left, right] 的值
abstract query(left: number, right: number): any
// 显示底层数组
abstract showArray(varName: string): any[]
// 获取线段树的根节点
abstract _getRoot(): SegmentNode | null
}下面的可视化面板创建了一个求和线段树，展示了线段树的逻辑结构、底层数组和基本操作 query, update：
并查集（Union Find）
UF 类可以创建并查集结构，用来解决图结构的动态连通性问题，底层原理见 并查集核心原理。
由于并查集结构有多种优化方式，比如路径压缩、按权重合并等，所以 UF 类提供了多种初始化方式：
UF.createNative(n: number)：创建一个未经优化的并查集结构，包含n个节点。UF.createWeighted(n: number)：创建一个权重数组优化的并查集结构，包含n个节点。UF.createPathCompression(n: number)：创建一个路径压缩优化的并查集结构，包含n个节点。
UF 对象主要有如下三个方法，用来解决动态连通性问题：
union(p: number, q: number)：合并两个节点p和q所在的连通分量。connected(p: number, q: number)：判断节点p和q是否在同一个连通分量中。count()：返回当前并查集中连通分量的数量。
并查集的逻辑结构是一个森林（若干棵多叉树），可视化面板为了方便展示，给这个森林创建了一个虚拟节点上，其中虚拟节点是透明的，每棵多叉树的根节点显示为红色，普通节点显示为绿色。这样就可以用一棵多叉树的形式展示森林结构，同时又能方便地看到每个连通分量的根节点。
并查集底层是用一个数组来实现森林的，调用 showArray 方法可以让可视化面板同时显示这个底层数组。
下面是使用权重数组优化的并查集的例子：
API 文档
abstract class UF {
// 创建一个大小为 n 的普通并查集
static createNaive(n: number): UF {
}
// 创建一个大小为 n 的加权并查集
static createWeighted(n: number): UF {
}
// 创建一个大小为 n 的路径压缩并查集
static createPathCompression(n: number): UF {
}
// 创建一个大小为 n 的并查集，默认使用路径压缩
static create(n: number): UF {
return UF.createPathCompression(n)
}
// 寻找 p 的根节点
find(p: number): number {
}
// 合并 p 和 q 所在的连通分量
union(p: number, q: number): void {
}
// 判断 p 和 q 是否在同一个连通分量
connected(p: number, q: number): boolean {
}
// 返回连通分量的数量
count(): number {
}
// 显示并查集的 parent 数组
showArray(varName: string): void {
}
}Trie 树/前缀树/字典树
Trie.create() 可以创建一棵 Trie 树，其中蓝色的节点是普通 Trie 节点，紫色的节点是包含单词的节点，鼠标移动到节点上可以显示该节点保存的单词。
API 文档
// 字典树节点
abstract class TrieNode {
abstract char: string
abstract isWord: boolean
abstract children: TrieNode[]
}
// 字典树 API
abstract class Trie {
// 创建一个字典树，words 中的单词将初始化到字典树中
static create(words?: string[]): Trie {
}
// 向字典树中添加字符串 word
add(word: string) {
}
// 从字典树中删除 word
remove(word: string) {
}
// 返回 word 的最短前缀
shortestPrefixOf(word: string) {
}
// 返回 word 的最长前缀
longestPrefixOf(word: string) {
}
// 判断是否存在以 prefix 为前缀的字符串
hasKeyWithPrefix(prefix: string) {
}
// 返回所有以 prefix 为前缀的字符串
keysWithPrefix(prefix: string) {
}
// 返回所有符合 pattern 的字符串
keysWithPattern(pattern: string) {
}
// 判断 word 是否存在于字典树中
containsKey(word: string) {
}
// 返回字典树中的字符串数量
size() {
}
}console.log 增强
我在很久之前分享过一种在笔试中仅使用标准输出调试递归算法的技巧，即使用额外的缩进来区分递归深度。
所以我在可视化面板中对 console.log 函数（JavaScript 的打印输出函数）进行了增强，方便大家更直观地观察复杂算法的输出。
具体加强如下：
1、如果你在可视化面板中使用 console.log，输出内容会被打印在左下角的 Log Console 中，且会根据递归深度自动添加缩进。
2、点击控制台中的输出，会有一条虚线标记对齐所有相同缩进的输出，方便你了解哪些输出是同一递归深度的。
代码在开始递归和结束递归的时候进行输出，可以看到左下角的控制台输出了如下内容，相同层数的递归函数中的输出都有相同的缩进，方便区分：
enter traverse(1)
enter traverse(2)
enter traverse(3)
enter traverse(4)
leave traverse(4)
leave traverse(3)
leave traverse(2)
leave traverse(1)你可以点击控制台中每行输出的第一个字符 e 或者 l，可以看到一条虚线标记对齐所有相同缩进的输出，更容易看出 enter 和 leave 的对应关系。
如果不想用自动缩进的功能，可以把代码中的 console.log 改成 console._log，这样输出就不会自动缩进了。你可以自己修改代码试一试。
排序算法可视化
@visualize shape nums rect 注释可以把数组按照元素大小转化成类似直方图的形式，有助于直观地感受数组元素的大小关系，以便观察排序算法的执行过程。使用 @visualize shape nums cycle 可以将数组元素转换回默认的圆形显示。
下面以 插入排序 为例：
变量绑定为数组索引
默认情况下，当变量名作为索引值访问数组时，该变量会自动绑定到数组上，数组上会出现一个游标显示该变量所指向的元素。但有些时候一个变量可能并不会访问数组元素，但我们依然希望让这个变量显示在数组上。
比如上面的插入排序可视化中的 sortedIndex 变量，代码中始终没有出现类似 nums[sortedIndex] 这样的数组访问，但我们希望 sortedIndex 变量在右侧可视化面板中显示，因为它是一个用来标记已排序元素和未排序元素边界的变量。
这种情况下，我们可以使用 @visualize bind nums[sortedIndex] 注释，将 sortedIndex 变量绑定到 nums 数组上，这样右侧 nums 数组上就会始终出现一个游标显示 sortedIndex 所在的位置。
如果希望解绑，可以使用 @visualize unbind nums[sortedIndex] 注释。
颜色系统
可以用 @visualize color 注释来设置节点/元素的颜色，颜色是一个以 # 开头的十六进制颜色代码（Hex Color Code），比如 #8ec7dd 就是浅蓝色。
颜色代码中可以出现 ?，表示一个随机的十六进制数，以此生成随机颜色，比如 #8e??dd。
比如上面的插入排序可视化中，我使用 @visualize color nums[sortedIndex] #8ec7dd 设置变量 sortedIndex 的颜色。即 sortedIndex 索引指向的数组元素会变成浅蓝色，当 sortedIndex 变量移到新的索引时，旧索引的元素会恢复默认颜色。
如果你想对数组的某个索引染色，不希望随着变量的移动而移动，要用 * 标记声明对固定元素染色，不随着变量移动。
比如 @visualize color *nums[0] #8ec7dd 或 @visualize color *nums[sortedIndex] #8ec7dd，当 sortedIndex = 2 时，nums[2] 会变成浅蓝色，无论 sortedIndex 的值如何变化，nums[2] 都会保持浅蓝色。
对于节点对象也是类似的，可以对变量染色，比如 @visualize color root #8ec7dd；或者对指定节点染色，比如 @visualize color *root.left #8ec7dd。
如果想取消设置的颜色，可以使用 unset 作为颜色代码，比如 @visualize color *root.left unset 注释，即可恢复默认颜色。
通过 @visualize color 注释设置颜色后，颜色代码会被显示成一个颜色选择器，你也可以点击颜色选择器来修改颜色。
变量隐藏和作用域提升
使用 @visualize global 可以将变量的作用域提升到全局，这样，一些闭包变量就可以一直显示在右侧的可视化面板中。
使用 @visualize hide 可以隐藏变量，这样，你可以把一些无关的数据结构隐藏起来，避免右侧可视化面板过于拥挤。
用一个例子说明上面这两种注释的用法。比如说我想实现一个简单的 Stack 类，实现栈的 push, pop, peek 三个方法，我可以利用 JavaScript 函数的闭包这样来写：
但是拉到最后一步可以看到，stack 这个变量一直作为一个 Object 存在于右侧的可视化面板中，并没有什么实际意义，还占很大的地方。
其实我们更关心的是那个 items 变量，因为我们可以观察这个数组中元素变化的情况以了解 push, pop 方法是如何工作的。
然而由于 items 是在 Stack 函数内部声明的变量，所以当代码在函数体之外执行时，items 变量不在当前的作用域，所以右侧面板也不会把它可视化出来。
对于这种情况，我们可以使用 @visualize global 注释将 items 变量提升到全局作用域，然后用 @visualize hide 注释让 stack 变量在右侧面板中隐藏。
这样就可以达到我们想要的效果。请你点击 stack.push(1); 这行代码并往下执行，可以看到 stack 变量不会再出现，且 items 数组的更新过程会显示在右侧：
回溯/DFS 递归过程可视化
递归算法是很多读者头痛的，我之前写过一篇 从树的角度理解一切递归算法，从理论上抽象出了递归算法最基本的思维模型和编写技巧。
简单来说就是：把递归函数理解成递归树上的一个指针，回溯算法是在遍历一棵多叉树，并收集叶子节点的值；动态规划是在分解问题，用子问题的答案来推导原问题的答案。
现在，我把文章中所阐述的思维模型融入了算法可视化面板，一定可以让你更直观地理解递归算法的执行过程。
对于递归算法，@visualize status，@visualize choose 和 @visualize unchoose 这几种注释可以帮到大忙，下面一一介绍。
@visualize status 举例
一句话，@visualize status 注释可以放在需要可视化的递归函数的上方，用来控制递归树上节点的值。
看个最简单的例子，我在讲解 动态规划算法核心框架 时画出了斐波那契问题的递归树，上层规模较大的问题逐渐被分解：
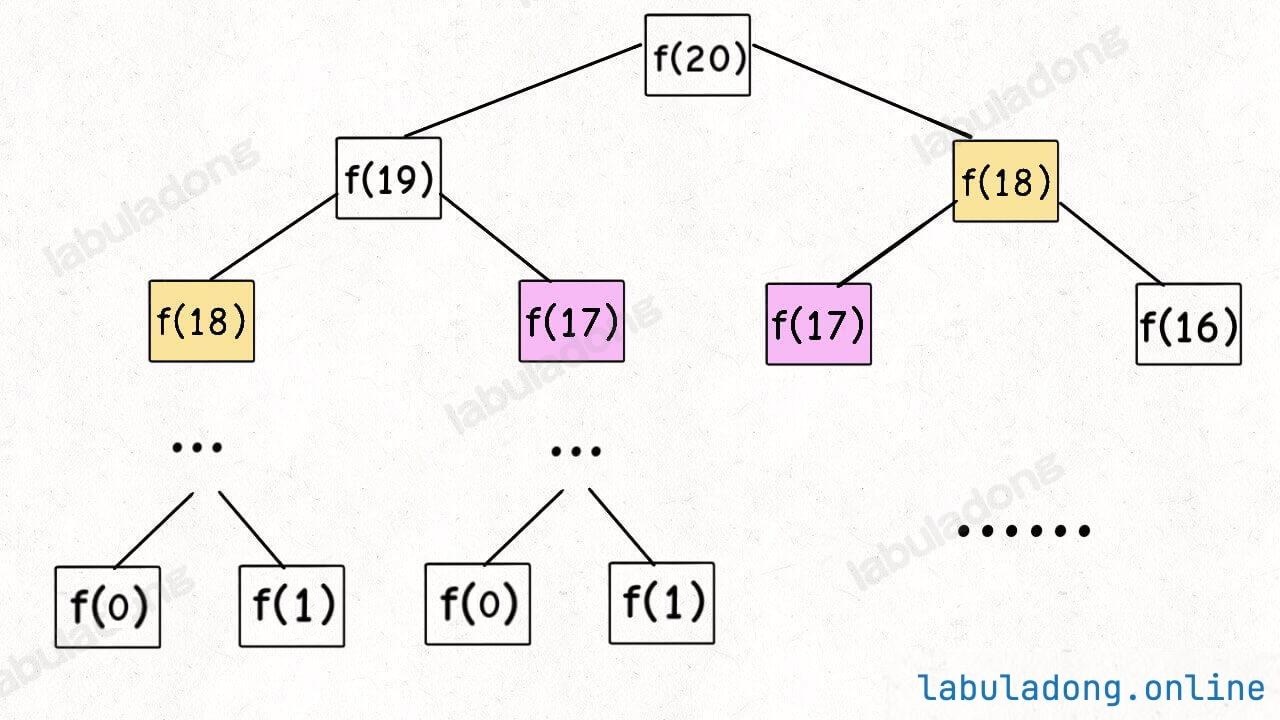
如何描述算法运行的过程？递归函数 fib 就好像递归树上的一个指针，它不断把原问题分解成子问题，当问题分解到 base case（叶子节点）时，开始逐层返回子问题的答案，推导出原问题的答案。
结合 @visualize status 注释，可以很直观地看到这个过程。下面这个面板是斐波那契算法的递归树，正在试图计算 fib(3) 的值：
@visualize status 注释写在 fib 函数上边，具体含义是：
1、对这个 fib 函数开启递归树可视化功能，每次递归调用会被可视化为递归树上的一个节点，函数参数中的 n 的值会作为状态显示在节点上。
2、fib 函数被视为一个遍历这棵递归树的指针，处于堆栈路径的树枝会加粗显示。
3、如果函数有返回值，那么当函数结束，计算出某个节点返回值时，鼠标移动到这个节点上，会显示该返回值。
实操
请你在步数栏输入 27 并敲回车，就可以跳转到第 27 步。把鼠标移动到节点 (2) 上，可以看到 fib(2) = 1，这说明 fib(2) 的值已经被计算出来了。
而处在递归路径上的 (5),(4),(3) 节点，它们的值还没被计算出来，你把鼠标移动上去也不会显示返回值。
实操
请你尝试点击可视化面板的前进后退按钮，让算法向后运行几步，理解动态规划算法的递归树生长过程。
实操
待到整棵递归树遍历完成之时，就是原问题 fib(5) 被计算出来之日，那时候整棵递归树上的所有节点都会显示返回值。
请你尝试拉动进度条到最后，看看这棵递归树的样子，并把鼠标移动到各个节点上，看看显示什么。
前面展示的斐波那契解法代码没有添加备忘录，是一个指数级时间复杂度的算法，现在我们来体验一下添加备忘录之后会对整棵递归树的生长产生什么影响。
实操
👇 请你拉动进度条到算法的最后，看看递归树长什么样子。
实操
👇 这是一个带备忘录优化的版本，请你拉动进度条到算法的最后，看看递归树长什么样子，和不带备忘录优化的递归树进行对比。
这样把整棵树可视化出来，你是不是就能很直观地理解动态规划通过备忘录消除重叠子问题的原理了？
@visualize choose/unchoose 举例
一句话，@visualize choose/unchoose 注释分别放在递归函数调用之前和之后，控制递归树树枝上的值。
我编一个简单的回溯算法的题目吧，比如让你写一个 generateBinaryNumber 函数，生成长度为 n 的二进制数，比如 n = 3 时，生成 000, 001, 010, 011, 100, 101, 110, 111 这 8 个二进制数。
这道题的解法代码也不复杂，我来展示一下如何用 @visualize choose/unchoose 注释来可视化回溯过程的：
你可以把鼠标移动到递归树上的任意节点，就可以显示出从根节点到该节点的路径上的所有信息。
你结合这棵递归树去理解递归算法的代码，是不是就很直观了？
BFS 过程可视化
正如 二叉树思维（纲领篇） 所说，BFS 算法是从二叉树的层序遍历扩展而来。
既然递归树都可以可视化出来，那么 BFS 过程也可以可视化出来。你可以使用 @visualize bfs 开启 BFS 算法的可视化自动生成穷举树。节点上的值是队列中元素的值，用 @visualize choose/unchoose 注释可以控制树枝上的值。
下面我用一个简单的例子来展示 BFS 过程的可视化：
场景练习题
下面我会结合具体的算法题目，向你提问，要求你利用可视化面板高效分析题目和算法的执行过程。我会给出问题的答案，你可以先自己思考，然后再看我的解答。
这部分主要用到的是可视化面板的「执行到指定代码位置」的功能：你可以点击代码的某一部分，然后算法就会执行到那里，并将执行过程可视化。这个功能用得好，可以大幅提升你对算法的理解。
热身
首先，我带大家熟悉一下「执行到指定代码位置」的功能，在之前展示的单链表成环算法中，我其实已经带你用过了，我让你不断点击代码中的 if (slow === fast) 这一行，观看快板指针的追逐过程：
为什么点击这部分就可以展示快慢指针的追逐呢？因为执行这部分代码时，fast, slow 指针刚刚移动完毕，所以点击这里，可以看到它们最完整的移动过程。
在下面的练习中，请你着重思考代码执行到某一部分时算法的状态，这样你就能更好地利用可视化面板，精确地控制算法的执行。
场景一：二叉树的前中后序遍历
实操
上面这段代码是二叉树前中后序遍历，相信大家都不陌生。
请你点击播放按钮，查看这段代码的执行流程。播放时，上一步/下一步按钮将变成加速/减速按钮，用来调整播放速度。
提问
你可以看到，二叉树将会被可视化出来，root 变量就好像一个指针，在二叉树上游走。我希望你能够使用「执行到指定代码位置」的功能，点击代码中的合适位置，精确控制 root 指针的移动顺序。
1、把面板复位，让 root 指针按照前序顺序访问整棵二叉树，即 root 指针按照 1,2,4,3,5,6 的顺序遍历二叉树。
2、把面板复位，root 指针按照中序顺序访问整棵二叉树，即 root 指针按照 2,4,1,5,3,6 的顺序遍历二叉树。
3、把面板复位，root 指针按照后序顺序访问整棵二叉树，即 root 指针按照 4,2,5,6,3,1 的顺序遍历二叉树。
答案
这几个问题不难：
1、不断点击 preorderResult.push(root.val) 这部分代码。
2、不断点击 inorderResult.push(root.val) 这部分代码。
3、不断点击 postorderResult.push(root.val) 这部分代码。
场景二：观察递归树的生长
提问
👇 这是刚才讲到的不带备忘录的斐波那契算法，现在请结合你对递归树的理解，点击代码中的合适位置，使得每点击一次，递归树就向下生长一个节点，直到递归树完全长成。
答案
你可以不断点击代码中 if (n < 2) 这一行，观察递归树的生长过程。
为什么点击这部分就可以展示递归树的生长过程呢？因为这部分代码是递归函数的 base case，每次递归必然都会执行这个判断逻辑，而递归树的每个节点其实就对应着每次递归，所以点击这个 if 语句就可以看到递归树上节点的生长过程。
这是一个非常常用的技巧，可以用来观察递归过程。
场景三：快速获得一个穷举结果
提问一
👇 这是前文展示的全排列算法的可视化面板，在场景二中你观察了斐波那契问题的递归树生长，现在请你点击代码中的合适位置，观察全排列问题的递归树生长。
答案一
这个很简单，不断点击 if (track.length === nums.length) 这部分代码即可观察递归树的生长。
提问二
将面板复位。
现在，我不想看递归树一个一个节点地生长了，没什么意思，我希望你点击代码中的合适位置，每点击一次，递归树就生长出一条「树枝」。
这是个回溯算法中很常见的场景哦，因为每条「树枝」的末端是叶子节点，而叶子节点一般就存储这回溯算法穷举出来的一个结果。比如你看这道题，每条树枝末端的叶子节点就是一个排列结果。
答案二
不断点击 res.push([...track]) 这部分代码，每次点击，回溯树都将生长出一条「树枝」。
因为叶子节点其实就是递归树结束生长的节点，即 backtrack 函数的 base case。那么我们只要点击 base case 中的代码，就可以直接跳到递归树的叶子节点，也就相当于生长出了一条树枝。
场景四：理解自顶向下/自底向上两种思维模式
提问
我在 动态规划核心框架 中讲过，自顶向下用 memo 备忘录的递归解法和自底向上用 dp 数组的迭代解法本质上是一样的，dp 数组中的值和 memo 备忘录中的值完全一样，两种解法可以互相转化。
下面我将同时给你自顶向下的递归解法和自底向上的迭代解法，请你完成如下题目：
1、在自顶向下递归解法的面板上，点击代码的合适位置，使得每次点击都在 memo 中更新一个元素。
2、在自底向上迭代解法的面板上，点击代码的合适位置，使得每次点击都在 dp 中更新一个元素。
3、对比两个解法中 dp 数组和 memo 数组的更新，理解自顶向下的递归解法和自底向上的迭代解法本质上是相同的。
答案
1、在自顶向下递归解法的面板上，每次点击 memo[n] = dp(memo, n - 1) + dp(memo, n - 2) 这部分代码，都会在 memo 数组中更新一个元素。
2、在自底向上迭代解法的面板上，每次点击 dp[i] = dp[i - 1] + dp[i - 2] 这部分代码，都会在 dp 数组中更新一个元素。
3、结合可视化面板应该不难理解，不过你会发现 memo[1] 和 dp[1] 的值不一样，那是因为我们把 dp[1] 作为 base case 设置了初始值，而递归解法中的 base case 是直接 return 的，并不需要设置在 memo 中。