速成读者学习规划
视频导读
这个视频会快速过一遍速成目录的内容,建议观看。

有些读者跟我反馈:本站的内容确实够扎实了,如果认真学习,必然可以彻底掌握数据结构和算法,但他们现在的问题是没有那么多时间,何解?
能不能抓大放小,先把必知必会的技巧学会,临阵磨枪快速提升一下,日后有时间再慢慢学习?我觉得这确实是相当一部分读者的需求,所以专门写了这个精简的速成规划。
如果你时间充裕,且对算法有一定的兴趣,那么可以按照 初学者规划 完整学习本站的目录内容。
如果你准备算法的时间不充裕,或者在纠结到底该选 初学者规划 还是 速成规划,那么不用犹豫,直接跟速成规划吧。不要贪多嚼不烂,先把速成规划中的内容掌握好,如果还有时间和兴趣的话,可以再回头学习本站的其他内容,这并不冲突。
速成规划的文章和题目已经整理到这个路线图里,点击图中节点即可展开相关教程和题单,方便你追踪进度和复习:
提示
由于路线图是树形结构,而目录是线性结构,所以路线图中的编排顺序和下面给出的目录有所不同,但内容是完全相同的,你可以选择自己喜欢的形式进行学习。
算法速成路线图
关于题单
经常有读者问公司题单相关的问题,所以这里多说几句。
速成目录包含必知必会的算法套路 + 经典算法题,不局限于具体某家公司的题单。目的是从根本上搞定算法这个硬骨头,让你能够独立解决中等难度的常考算法题,而不是依赖运气和记忆,死记硬背某个题单。
有些读者准备算法,上来就刷公司题单,这是不对的。我的建议是,你先把常见的算法框架学明白,下一步,再考虑刷题单。
不同公司的题单内容和难度不一样,但是算法本身也就那么些框架套路。你把套路都掌握了,一个题单最多也就两三个小时就刷完了,没啥神奇的。
题单只有两个价值:
1、提前了解公司考题的难度及算法类别。比方说你的公司明确说了不会考察动态规划算法,那么你可以跳过本目录的动态规划部分,把时间花在其他算法技巧上。
2、方便复习。学完算法框架之后就可以独立解题了,此时可以独立刷几遍题单,用来检验学习效果,巩固知识点。
速成目录涉及的题目看起来比较多,但大多都是框架题,学完教程后顺手就能全部做完,不用单独去刷。
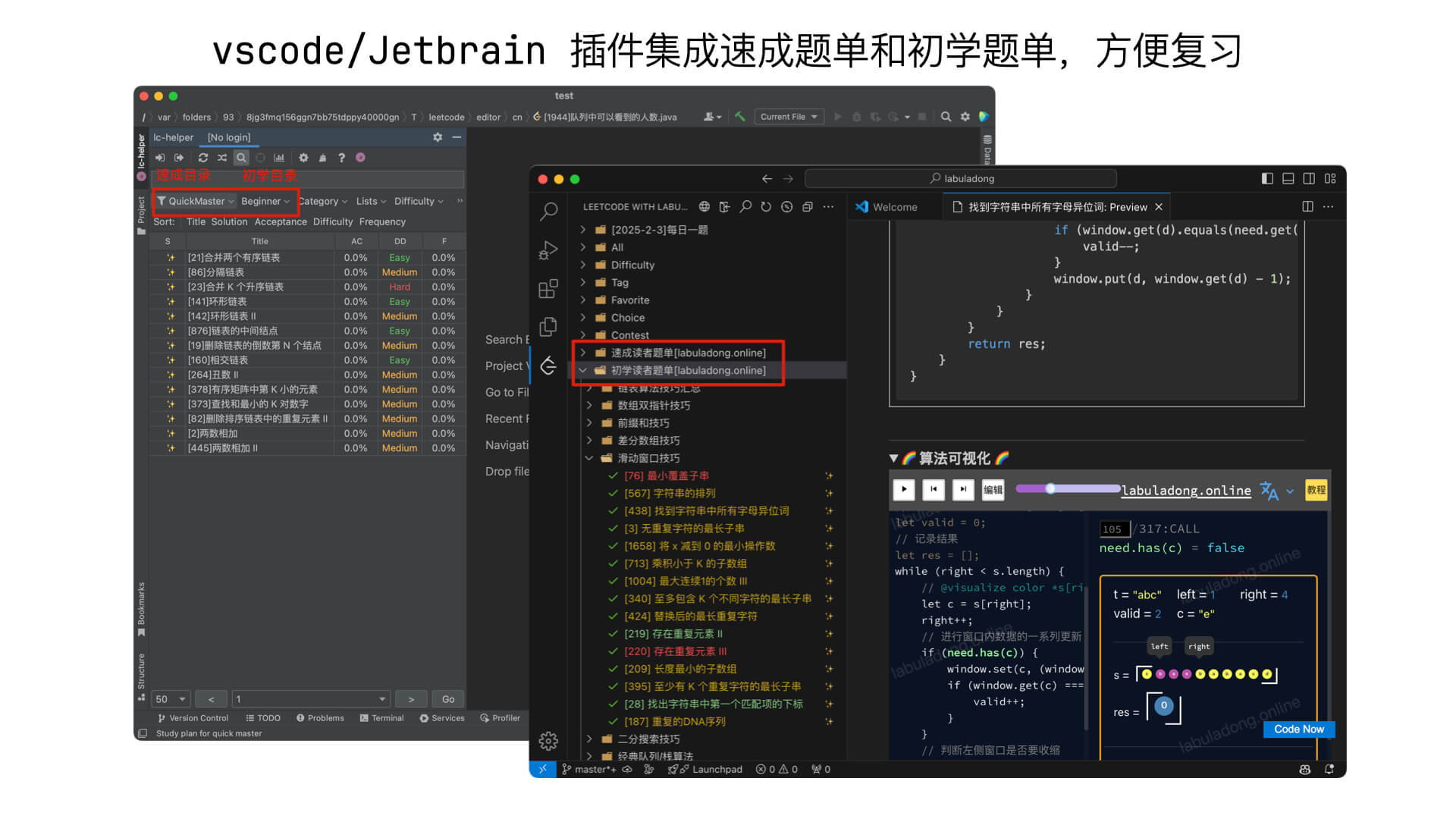
本站插件对速成目录的题目进行了整合,安装 Chrome 插件 后,浏览器打开力扣题目页面将显示本站的思路讲解,vscode 插件 和 Jetbrains 插件 中也集成了这个速成目录的题目列表
速成目录的原理
为什么速成目录能够在短时间内快速提升算法能力?
1、基于模板框架,统一的解法风格。
这个速成目录不是简单的题目列表,而是针对每个算法总结出一套框架模板,习题都使用统一的流程框架进行求解。你学会的是真正的算法解题能力而不是死记硬背,所以你不会局限于具体的题目列表,而是能够收发自如,独立解决没见过的题目。
2、循序渐进,由浅入深,同时包含数据结构和算法。
一个算法技巧 A,可能是算法 B 和算法 C 融合而来的,不给你任何背景铺垫直接讲 A,你就觉得算法高深莫测不可捉摸。但如果把 B 和 C 的基础补齐,你自己都能推导出 A,简直太简单了,有什么了不起的么。
比方很多读者畏惧递归算法,我就多次强调,算法的本质是穷举,递归是基于树结构的一种经典穷举手段,你只要把二叉树结构玩明白,就能玩明白一切递归算法。所以本目录会先从关键数据结构入手,然后再开始刷题。先把基础补齐,刷题就会顺畅高效。
3、科学的学习方法,丰富的辅助工具。例题和习题配合,先讲后练,结合刷题插件、可视化面板,尽一切努力帮助读者降低理解成本,提高学习效率。
再次强调,我非常理解有些读者时间紧迫,但是你不要图省事,不学框架就直接刷题。
只刷题单的问题在于过度依赖运气。运气好遇到原题的话,也许你能默写出解法;一旦没有运气加持,就得靠算法框架解题,你没学过就凉凉了。所谓基础不牢地动山摇,一开始先花时间把基础夯实,算总账反而是最省时间的。
下面就开始吧,速成目录主要分「数据结构」部分和「算法刷题」部分:数据结构部分基本不涉及算法题,相对较简单;刷题部分是重点,一定要认真思考,亲自动手实践。
关于建议用时
下面对每篇文章的建议用时是一个偏大的粗略的估计,假设读者时间并不充裕,每天只花碎片化的 1~2 小时左右的时间学习。
所以这个建议用时仅供参考,具体的学习时间会根据每个人有所差异,如果能够花整块的完整时间学习,速度会快很多。
另外,速成读者不要过度死磕。有些东西不可能完全靠自己想出来的,第一次学习时主要以理解和模仿为主,跟着网站的思路把整个知识体系建立起来;到时候回头再看,很多问题自然就迎刃而解了。
数据结构
数组链表
介绍基本的数组链表概念,比较简单。主要是环形数组这个技巧是重点,可以用 的时间复杂度在数组头部进行插入删除操作。
关键基础,建议用时 1 天
哈希表原理及应用
作为速成教程,我们可以跳过哈希表的两种解决哈希冲突的代码实现,但是哈希表的原理是必须掌握的。
哈希表可以和数组、双链表进行结合,形成更强大的数据结构 LinkedHashMap 和 ArrayHashMap,它们可以给哈希表增加新的特性,你要了解其中的原理,遇到对应的使用场景时,就知道有这么一个工具可以使用。
关键基础,建议用时 1~2 天
二叉树基础及遍历
虽然现在只是基础知识章节,但是二叉树部分必须重视起来,尤其是二叉树的遍历,是入门递归思维关键。后面开始刷题后,所有递归算法的本质上都是二叉树的遍历。
关键基础,建议用时 1~2 天
层序遍历的三种写法模板
第一种,最简单的写法:
void levelOrderTraverse(TreeNode root) {
if (root == null) {
return;
}
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
while (!q.isEmpty()) {
TreeNode cur = q.poll();
// 访问 cur 节点
System.out.println(cur.val);
// 把 cur 的左右子节点加入队列
if (cur.left != null) {
q.offer(cur.left);
}
if (cur.right != null) {
q.offer(cur.right);
}
}
}void levelOrderTraverse(TreeNode* root) {
if (root == nullptr) {
return;
}
std::queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
TreeNode* cur = q.front();
q.pop();
// 访问 cur 节点
std::cout << cur->val << std::endl;
// 把 cur 的左右子节点加入队列
if (cur->left != nullptr) {
q.push(cur->left);
}
if (cur->right != nullptr) {
q.push(cur->right);
}
}
}from collections import deque
def levelOrderTraverse(root):
if root is None:
return
q = deque()
q.append(root)
while q:
cur = q.popleft()
# 访问 cur 节点
print(cur.val)
# 把 cur 的左右子节点加入队列
if cur.left is not None:
q.append(cur.left)
if cur.right is not None:
q.append(cur.right)func levelOrderTraverse(root *TreeNode) {
if root == nil {
return
}
q := []*TreeNode{}
q = append(q, root)
for len(q) > 0 {
cur := q[0]
q = q[1:]
// 访问 cur 节点
fmt.Println(cur.Val)
// 把 cur 的左右子节点加入队列
if cur.Left != nil {
q = append(q, cur.Left)
}
if cur.Right != nil {
q = append(q, cur.Right)
}
}
}var levelOrderTraverse = function(root) {
if (root === null) {
return;
}
var q = [];
q.push(root);
while (q.length !== 0) {
var cur = q.shift();
// 访问 cur 节点
console.log(cur.val);
// 把 cur 的左右子节点加入队列
if (cur.left !== null) {
q.push(cur.left);
}
if (cur.right !== null) {
q.push(cur.right);
}
}
}第二种,可以利用 step 记录层数信息,较常用:
void levelOrderTraverse(TreeNode root) {
if (root == null) {
return;
}
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
// 记录当前遍历到的层数(根节点视为第 1 层)
int depth = 1;
while (!q.isEmpty()) {
int sz = q.size();
for (int i = 0; i < sz; i++) {
TreeNode cur = q.poll();
// 访问 cur 节点,同时知道它所在的层数
System.out.println("depth = " + depth + ", val = " + cur.val);
// 把 cur 的左右子节点加入队列
if (cur.left != null) {
q.offer(cur.left);
}
if (cur.right != null) {
q.offer(cur.right);
}
}
depth++;
}
}void levelOrderTraverse(TreeNode* root) {
if (root == nullptr) {
return;
}
queue<TreeNode*> q;
q.push(root);
// 记录当前遍历到的层数(根节点视为第 1 层)
int depth = 1;
while (!q.empty()) {
int sz = q.size();
for (int i = 0; i < sz; i++) {
TreeNode* cur = q.front();
q.pop();
// 访问 cur 节点,同时知道它所在的层数
cout << "depth = " << depth << ", val = " << cur->val << endl;
// 把 cur 的左右子节点加入队列
if (cur->left != nullptr) {
q.push(cur->left);
}
if (cur->right != nullptr) {
q.push(cur->right);
}
}
depth++;
}
}from collections import deque
def levelOrderTraverse(root):
if root is None:
return
q = deque()
q.append(root)
# 记录当前遍历到的层数(根节点视为第 1 层)
depth = 1
while q:
sz = len(q)
for i in range(sz):
cur = q.popleft()
# 访问 cur 节点,同时知道它所在的层数
print(f"depth = {depth}, val = {cur.val}")
# 把 cur 的左右子节点加入队列
if cur.left is not None:
q.append(cur.left)
if cur.right is not None:
q.append(cur.right)
depth += 1func levelOrderTraverse(root *TreeNode) {
if root == nil {
return
}
q := []*TreeNode{root}
// 记录当前遍历到的层数(根节点视为第 1 层)
depth := 1
for len(q) > 0 {
// 获取当前队列长度
sz := len(q)
for i := 0; i < sz; i++ {
// 弹出队列头
cur := q[0]
q = q[1:]
// 访问 cur 节点,同时知道它所在的层数
fmt.Printf("depth = %d, val = %d\n", depth, cur.Val)
// 把 cur 的左右子节点加入队列
if cur.Left != nil {
q = append(q, cur.Left)
}
if cur.Right != nil {
q = append(q, cur.Right)
}
}
depth++
}
}var levelOrderTraverse = function(root) {
if (root === null) {
return;
}
let q = [];
q.push(root);
// 记录当前遍历到的层数(根节点视为第 1 层)
let depth = 1;
while (q.length !== 0) {
let sz = q.length;
for (let i = 0; i < sz; i++) {
let cur = q.shift();
// 访问 cur 节点,同时知道它所在的层数
console.log("depth = " + depth + ", val = " + cur.val);
// 把 cur 的左右子节点加入队列
if (cur.left !== null) {
q.push(cur.left);
}
if (cur.right !== null) {
q.push(cur.right);
}
}
depth++;
}
};第三种,使用自定义 State 类维护每个节点的信息,复杂一些但最灵活,会在图算法或复杂 BFS 算法中见到:
class State {
TreeNode node;
int depth;
State(TreeNode node, int depth) {
this.node = node;
this.depth = depth;
}
}
void levelOrderTraverse(TreeNode root) {
if (root == null) {
return;
}
Queue<State> q = new LinkedList<>();
// 根节点的路径权重和是 1
q.offer(new State(root, 1));
while (!q.isEmpty()) {
State cur = q.poll();
// 访问 cur 节点,同时知道它的路径权重和
System.out.println("depth = " + cur.depth + ", val = " + cur.node.val);
// 把 cur 的左右子节点加入队列
if (cur.node.left != null) {
q.offer(new State(cur.node.left, cur.depth + 1));
}
if (cur.node.right != null) {
q.offer(new State(cur.node.right, cur.depth + 1));
}
}
}class State {
public:
TreeNode* node;
int depth;
State(TreeNode* node, int depth) : node(node), depth(depth) {}
};
void levelOrderTraverse(TreeNode* root) {
if (root == nullptr) {
return;
}
queue<State> q;
// 根节点的路径权重和是 1
q.push(State(root, 1));
while (!q.empty()) {
State cur = q.front();
q.pop();
// 访问 cur 节点,同时知道它的路径权重和
cout << "depth = " << cur.depth << ", val = " << cur.node->val << endl;
// 把 cur 的左右子节点加入队列
if (cur.node->left != nullptr) {
q.push(State(cur.node->left, cur.depth + 1));
}
if (cur.node->right != nullptr) {
q.push(State(cur.node->right, cur.depth + 1));
}
}
}class State:
def __init__(self, node, depth):
self.node = node
self.depth = depth
def levelOrderTraverse(root):
if root is None:
return
q = deque()
# 根节点的路径权重和是 1
q.append(State(root, 1))
while q:
cur = q.popleft()
# 访问 cur 节点,同时知道它的路径权重和
print(f"depth = {cur.depth}, val = {cur.node.val}")
# 把 cur 的左右子节点加入队列
if cur.node.left is not None:
q.append(State(cur.node.left, cur.depth + 1))
if cur.node.right is not None:
q.append(State(cur.node.right, cur.depth + 1))type State struct {
node *TreeNode
depth int
}
func levelOrderTraverse(root *TreeNode) {
if root == nil {
return
}
q := []State{{root, 1}}
for len(q) > 0 {
cur := q[0]
q = q[1:]
// 访问 cur 节点,同时知道它的路径权重和
fmt.Printf("depth = %d, val = %d\n", cur.depth, cur.node.Val)
// 把 cur 的左右子节点加入队列
if cur.node.Left != nil {
q = append(q, State{cur.node.Left, cur.depth + 1})
}
if cur.node.Right != nil {
q = append(q, State{cur.node.Right, cur.depth + 1})
}
}
}function State(node, depth) {
this.node = node;
this.depth = depth;
}
var levelOrderTraverse = function(root) {
if (root === null) {
return;
}
// @visualize bfs
var q = [];
// 根节点的路径权重和是 1
q.push(new State(root, 1));
while (q.length !== 0) {
var cur = q.shift();
// 访问 cur 节点,同时知道它的路径权重和
console.log("depth = " + cur.depth + ", val = " + cur.node.val);
// 把 cur 的左右子节点加入队列
if (cur.node.left !== null) {
q.push(new State(cur.node.left, cur.depth + 1));
}
if (cur.node.right !== null) {
q.push(new State(cur.node.right, cur.depth + 1));
}
}
};二叉堆原理
二叉堆的关键应用是优先级队列。作为速成教程,我们可以跳过优先级队列的实现,但是要理解以下关键点:
1、优先级队列是一种能够自动排序的数据结构,增删元素的复杂度是 ,底层使用二叉堆实现。
2、二叉堆是一种拥有特殊性质的完全二叉树。
3、优先级队列(二叉堆)的核心方法是 swim, sink,用来维护二叉堆的性质。
关键基础,建议用时 0.5 天
图结构
图论算法是一个很大的话题,但是作为数据结构基础章节,我们目前只需要了解图的逻辑表示和具体实现,以及图的遍历算法。
其实也不算复杂,本质上还是前文二叉树结构的延伸,下面这两篇文章给出了图结构的通用实现和遍历算法模板。
关键基础,建议用时 1 天
开始刷题
现在开始刷题,如果你是第一次接触在线刷题平台,可以先看一下 力扣/LeetCode 解题须知 了解力扣刷题的基本规则。
核心框架,建议用时 0.5 天
这篇文章是本站全站内容的纲领,不仅会对上面介绍的数据结构进行总结,还会直接指出所有算法的本质。
其中会出现大量其他文章的链接引用,初次阅读肯定不容易完全理解,但是不必死磕,只要大致了解文中介绍的思维方法即可,在学习后面内容的时候你将会逐渐领会到本文的精髓。
链表
链表相关的题目套路比较固定,主要是双指针技巧。
核心框架,建议用时 1 天
习题,建议用时 1 天
单链表的一个进阶技巧是递归操作单链表,不过这种思路一般用于面试时说一下就行,笔试时就用标准的指针操作即可。
核心框架,建议用时 1 天
数组
数组相关的技巧也主要是双指针,只不过可以分为快慢指针、左右指针几种不同的类型。经典的数组双指针算法有二分搜索、滑动窗口。
有些读者问我为什么不出字符串算法的专题,因为字符串就是字符数组,字符串算法本质上还是数组算法。
核心框架,建议用时 0.5 天
习题,建议用时 1~2 天
核心框架,建议用时 1 天
滑动窗口代码模板(伪码)
// 滑动窗口算法伪码框架
void slidingWindow(String s) {
// 用合适的数据结构记录窗口中的数据,根据具体场景变通
// 比如说,我想记录窗口中元素出现的次数,就用 map
// 如果我想记录窗口中的元素和,就可以只用一个 int
Object window = ...
int left = 0, right = 0;
while (right < s.length()) {
// c 是将移入窗口的字符
char c = s[right];
window.add(c)
// 增大窗口
right++;
// 进行窗口内数据的一系列更新
...
// *** debug 输出的位置 ***
// 注意在最终的解法代码中不要 print
// 因为 IO 操作很耗时,可能导致超时
printf("window: [%d, %d)\n", left, right);
// ***********************
// 判断左侧窗口是否要收缩
while (left < right && window needs shrink) {
// d 是将移出窗口的字符
char d = s[left];
window.remove(d)
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
...
}
}
}// 滑动窗口算法伪码框架
void slidingWindow(string s) {
// 用合适的数据结构记录窗口中的数据,根据具体场景变通
// 比如说,我想记录窗口中元素出现的次数,就用 map
// 如果我想记录窗口中的元素和,就可以只用一个 int
auto window = ...
int left = 0, right = 0;
while (right < s.size()) {
// c 是将移入窗口的字符
char c = s[right];
window.add(c);
// 增大窗口
right++;
// 进行窗口内数据的一系列更新
...
// *** debug 输出的位置 ***
printf("window: [%d, %d)\n", left, right);
// 注意在最终的解法代码中不要 print
// 因为 IO 操作很耗时,可能导致超时
// 判断左侧窗口是否要收缩
while (window needs shrink) {
// d 是将移出窗口的字符
char d = s[left];
window.remove(d);
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
...
}
}
}# 滑动窗口算法伪码框架
def slidingWindow(s: str):
# 用合适的数据结构记录窗口中的数据,根据具体场景变通
# 比如说,我想记录窗口中元素出现的次数,就用 map
# 如果我想记录窗口中的元素和,就可以只用一个 int
window = ...
left, right = 0, 0
while right < len(s):
# c 是将移入窗口的字符
c = s[right]
window.add(c)
# 增大窗口
right += 1
# 进行窗口内数据的一系列更新
...
# *** debug 输出的位置 ***
# 注意在最终的解法代码中不要 print
# 因为 IO 操作很耗时,可能导致超时
# print(f"window: [{left}, {right})")
# ***********************
# 判断左侧窗口是否要收缩
while left < right and window needs shrink:
# d 是将移出窗口的字符
d = s[left]
window.remove(d)
# 缩小窗口
left += 1
# 进行窗口内数据的一系列更新
...// 滑动窗口算法伪码框架
func slidingWindow(s string) {
// 用合适的数据结构记录窗口中的数据,根据具体场景变通
// 比如说,我想记录窗口中元素出现的次数,就用 map
// 如果我想记录窗口中的元素和,就可以只用一个 int
var window = ...
left, right := 0, 0
for right < len(s) {
// c 是将移入窗口的字符
c := rune(s[right])
window[c]++
// 增大窗口
right++
// 进行窗口内数据的一系列更新
...
// *** debug 输出的位置 ***
// 注意在最终的解法代码中不要 print
// 因为 IO 操作很耗时,可能导致超时
fmt.Println("window: [",left,", ",right,")")
// ***********************
// 判断左侧窗口是否要收缩
for left < right && window needs shrink {
// d 是将移出窗口的字符
d := rune(s[left])
window[d]--
// 缩小窗口
left++
// 进行窗口内数据的一系列更新
...
}
}
}// 滑动窗口算法伪码框架
var slidingWindow = function(s) {
// 用合适的数据结构记录窗口中的数据,根据具体场景变通
// 比如说,我想记录窗口中元素出现的次数,就用 map
// 如果我想记录窗口中的元素和,就可以只用一个 int
var window = ...;
var left = 0, right = 0;
while (right < s.length) {
// c 是将移入窗口的字符
var c = s[right];
window.add(c);
// 增大窗口
right++;
// 进行窗口内数据的一系列更新
...
// *** debug 输出的位置 ***
// 注意在最终的解法代码中不要 print
// 因为 IO 操作很耗时,可能导致超时
console.log("window: [%d, %d)\n", left, right);
// *********************
// 判断左侧窗口是否要收缩
while (window needs shrink) {
// d 是将移出窗口的字符
var d = s[left];
window.remove(d);
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
...
}
}
};习题,建议用时 1 天
核心框架,建议用时 1~2 天
二分搜索三种代码模板
int binary_search(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while(left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if(nums[mid] == target) {
// 直接返回
return mid;
}
}
// 直接返回
return -1;
}
int left_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 别返回,锁定左侧边界
right = mid - 1;
}
}
// 判断 target 是否存在于 nums 中
if (left < 0 || left >= nums.length) {
return -1;
}
// 判断一下 nums[left] 是不是 target
return nums[left] == target ? left : -1;
}
int right_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 别返回,锁定右侧边界
left = mid + 1;
}
}
// 由于 while 的结束条件是 right == left - 1,且现在在求右边界
// 所以用 right 替代 left - 1 更好记
if (right < 0 || right >= nums.length) {
return -1;
}
return nums[right] == target ? right : -1;
}int binary_search(vector<int>& nums, int target) {
int left = 0, right = nums.size()-1;
while(left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if(nums[mid] == target) {
// 直接返回
return mid;
}
}
// 直接返回
return -1;
}
int left_bound(vector<int>& nums, int target) {
int left = 0, right = nums.size()-1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 别返回,锁定左侧边界
right = mid - 1;
}
}
// 判断 target 是否存在于 nums 中
if (left < 0 || left >= nums.size()) {
return -1;
}
// 判断一下 nums[left] 是不是 target
return nums[left] == target ? left : -1;
}
int right_bound(vector<int>& nums, int target) {
int left = 0, right = nums.size()-1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 别返回,锁定右侧边界
left = mid + 1;
}
}
// 由于 while 的结束条件是 right == left - 1,且现在在求右边界
// 所以用 right 替代 left - 1 更好记
if (right < 0 || right >= nums.size()) {
return -1;
}
return nums[right] == target ? right : -1;
}def binary_search(nums: List[int], target: int) -> int:
# 设置左右下标
left, right = 0, len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
right = mid - 1
elif nums[mid] == target:
# 找到目标值
return mid
# 没有找到目标值
return -1
def left_bound(nums: List[int], target: int) -> int:
# 设置左右下标
left, right = 0, len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
right = mid - 1
elif nums[mid] == target:
# 存在目标值,缩小右边界
right = mid - 1
# 判断是否存在目标值
if left < 0 or left >= len(nums):
return -1
# 判断找到的左边界是否是目标值
return left if nums[left] == target else -1
def right_bound(nums: List[int], target: int) -> int:
# 设置左右下标
left, right = 0, len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
right = mid - 1
elif nums[mid] == target:
# 存在目标值,缩小左边界
left = mid + 1
# 判断是否存在目标值
if right < 0 or right >= len(nums):
return -1
# 判断找到的右边界是否是目标值
return right if nums[right] == target else -1func binarySearch(nums []int, target int) int {
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right - left) / 2
if nums[mid] < target {
left = mid + 1
} else if nums[mid] > target {
right = mid - 1
} else if nums[mid] == target {
// 直接返回
return mid
}
}
// 直接返回
return -1
}
func leftBound(nums []int, target int) int {
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right - left) / 2
if nums[mid] < target {
left = mid + 1
} else if nums[mid] > target {
right = mid - 1
} else if nums[mid] == target {
// 别返回,锁定左侧边界
right = mid - 1
}
}
// 判断 target 是否存在于 nums 中
if left < 0 || left >= len(nums) {
return -1
}
// 判断一下 nums[left] 是不是 target
if nums[left] == target {
return left
}
return -1
}
func rightBound(nums []int, target int) int {
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right - left) / 2
if nums[mid] < target {
left = mid + 1
} else if nums[mid] > target {
right = mid - 1
} else if nums[mid] == target {
// 别返回,锁定右侧边界
left = mid + 1
}
}
if right < 0 || right >= len(nums) {
return -1
}
if nums[right] == target {
return right
}
return -1
}var binary_search = function(nums, target) {
var left = 0, right = nums.length - 1;
while(left <= right) {
var mid = left + Math.floor((right - left) / 2);
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if(nums[mid] == target) {
// 直接返回
return mid;
}
}
// 直接返回
return -1;
}
var left_bound = function(nums, target) {
var left = 0, right = nums.length - 1;
while (left <= right) {
var mid = left + Math.floor((right - left) / 2);
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 别返回,锁定左侧边界
right = mid - 1;
}
}
// 判断 target 是否存在于 nums 中
if (left < 0 || left >= nums.length) {
return -1;
}
// 判断一下 nums[left] 是不是 target
return nums[left] == target ? left : -1;
}
var right_bound = function(nums, target) {
var left = 0, right = nums.length - 1;
while (left <= right) {
var mid = left + Math.floor((right - left) / 2);
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// 别返回,锁定右侧边界
left = mid + 1;
}
}
// 由于 while 的结束条件是 right == left - 1,且现在在求右边界
// 所以用 right 替代 left - 1 更好记
if (right < 0 || right >= nums.length) {
return -1;
}
return nums[right] == target ? right : -1;
}核心框架,建议用时 1~2 天
前缀和数组代码模板
一维前缀和:
class NumArray {
// 前缀和数组
private int[] preSum;
// 输入一个数组,构造前缀和
public NumArray(int[] nums) {
// preSum[0] = 0,便于计算累加和
preSum = new int[nums.length + 1];
// 计算 nums 的累加和
for (int i = 1; i < preSum.length; i++) {
preSum[i] = preSum[i - 1] + nums[i - 1];
}
}
// 查询闭区间 [left, right] 的累加和
public int sumRange(int left, int right) {
return preSum[right + 1] - preSum[left];
}
}#include <vector>
class NumArray {
// 前缀和数组
std::vector<int> preSum;
// 输入一个数组,构造前缀和
public:
NumArray(std::vector<int>& nums) {
// preSum[0] = 0,便于计算累加和
preSum.resize(nums.size() + 1);
// 计算 nums 的累加和
for (int i = 1; i < preSum.size(); i++) {
preSum[i] = preSum[i - 1] + nums[i - 1];
}
}
// 查询闭区间 [left, right] 的累加和
int sumRange(int left, int right) {
return preSum[right + 1] - preSum[left];
}
};class NumArray:
# 前缀和数组
def __init__(self, nums: List[int]):
# 输入一个数组,构造前缀和
# preSum[0] = 0,便于计算累加和
self.preSum = [0] * (len(nums) + 1)
# 计算 nums 的累加和
for i in range(1, len(self.preSum)):
self.preSum[i] = self.preSum[i - 1] + nums[i - 1]
# 查询闭区间 [left, right] 的累加和
def sumRange(self, left: int, right: int) -> int:
return self.preSum[right + 1] - self.preSum[left]type NumArray struct {
// 前缀和数组
PreSum []int
}
// 输入一个数组,构造前缀和
func Constructor(nums []int) NumArray {
// PreSum[0] = 0,便于计算累加和
preSum := make([]int, len(nums)+1)
// 计算 nums 的累加和
for i := 1; i < len(preSum); i++ {
preSum[i] = preSum[i-1] + nums[i-1]
}
return NumArray{PreSum: preSum}
}
// 查询闭区间 [left, right] 的累加和
func (this *NumArray) SumRange(left int, right int) int {
// The following line includes the missing comment:
// preSum[0] = 0,便于计算累加和
return this.PreSum[right+1] - this.PreSum[left] // Here we are using the prefix sum property, no need to repeat the comment here.
}var NumArray = function(nums) {
// 前缀和数组
let preSum = new Array(nums.length + 1).fill(0);
// preSum[0] = 0,便于计算累加和
preSum[0] = 0;
// 输入一个数组,构造前缀和
for (let i = 1; i < preSum.length; i++) {
// 计算 nums 的累加和
preSum[i] = preSum[i - 1] + nums[i - 1];
}
this.preSum = preSum;
};
// 查询闭区间 [left, right] 的累加和
NumArray.prototype.sumRange = function(left, right) {
return this.preSum[right + 1] - this.preSum[left];
};二维前缀和:
class NumMatrix {
// preSum[i][j] 记录矩阵 [0, 0, i-1, j-1] 的元素和
private int[][] preSum;
public NumMatrix(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
if (m == 0 || n == 0) return;
// 构造前缀和矩阵
preSum = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
// 计算每个矩阵 [0, 0, i, j] 的元素和
preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i - 1][j - 1] - preSum[i-1][j-1];
}
}
}
// 计算子矩阵 [x1, y1, x2, y2] 的元素和
public int sumRegion(int x1, int y1, int x2, int y2) {
// 目标矩阵之和由四个相邻矩阵运算获得
return preSum[x2+1][y2+1] - preSum[x1][y2+1] - preSum[x2+1][y1] + preSum[x1][y1];
}
}#include <vector>
class NumMatrix {
// preSum[i][j] 记录矩阵 [0, 0, i-1, j-1] 的元素和
std::vector<std::vector<int>> preSum;
public:
NumMatrix(std::vector<std::vector<int>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
if (m == 0 || n == 0) return;
// 构造前缀和矩阵
preSum.resize(m + 1, std::vector<int>(n + 1, 0));
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
// 计算每个矩阵 [0, 0, i, j] 的元素和
preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i - 1][j - 1] - preSum[i-1][j-1];
}
}
}
// 计算子矩阵 [x1, y1, x2, y2] 的元素和
int sumRegion(int x1, int y1, int x2, int y2) {
// 目标矩阵之和由四个相邻矩阵运算获得
return preSum[x2+1][y2+1] - preSum[x1][y2+1] - preSum[x2+1][y1] + preSum[x1][y1];
}
};class NumMatrix:
# preSum[i][j] 记录矩阵 [0, 0, i-1, j-1] 的元素和
def __init__(self, matrix: List[List[int]]):
m = len(matrix)
n = len(matrix[0])
if m == 0 or n == 0:
return
# 构造前缀和矩阵
self.preSum = [[0] * (n + 1) for _ in range(m + 1)]
for i in range(1, m + 1):
for j in range(1, n + 1):
# 计算每个矩阵 [0, 0, i, j] 的元素和
self.preSum[i][j] = (self.preSum[i - 1][j] + self.preSum[i][j - 1] +
matrix[i - 1][j - 1] - self.preSum[i - 1][j - 1])
# 计算子矩阵 [x1, y1, x2, y2] 的元素和
def sumRegion(self, x1: int, y1: int, x2: int, y2: int) -> int:
# 目标矩阵之和由四个相邻矩阵运算获得
return (self.preSum[x2 + 1][y2 + 1] - self.preSum[x1][y2 + 1] -
self.preSum[x2 + 1][y1] + self.preSum[x1][y1])type NumMatrix struct {
// preSum[i][j] 记录矩阵 [0, 0, i-1, j-1] 的元素和
preSum [][]int
}
func Constructor(matrix [][]int) NumMatrix {
m := len(matrix)
if m == 0 {
return NumMatrix{}
}
n := len(matrix[0])
if n == 0 {
return NumMatrix{}
}
// 构造前缀和矩阵
preSum := make([][]int, m+1)
for i := range preSum {
preSum[i] = make([]int, n+1)
}
for i := 1; i <= m; i++ {
for j := 1; j <= n; j++ {
// 计算每个矩阵 [0, 0, i, j] 的元素和
preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i-1][j-1] - preSum[i-1][j-1]
}
}
return NumMatrix{preSum: preSum}
}
// 计算子矩阵 [x1, y1, x2, y2] 的元素和
func (this *NumMatrix) SumRegion(x1, y1, x2, y2 int) int {
// 目标矩阵之和由四个相邻矩阵运算获得
return this.preSum[x2+1][y2+1] - this.preSum[x1][y2+1] - this.preSum[x2+1][y1] + this.preSum[x1][y1]
}var NumMatrix = function(matrix) {
let m = matrix.length, n = matrix[0].length;
// preSum[i][j] 记录矩阵 [0, 0, i-1, j-1] 的元素和
this.preSum = Array.from({length: m + 1}, () => Array(n + 1).fill(0));
if (m == 0 || n == 0) return;
// 构造前缀和矩阵
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
// 计算每个矩阵 [0, 0, i, j] 的元素和
this.preSum[i][j] = this.preSum[i-1][j] + this.preSum[i][j-1] + matrix[i - 1][j - 1] - this.preSum[i-1][j-1];
}
}
};
NumMatrix.prototype.sumRegion = function(x1, y1, x2, y2) {
// 计算子矩阵 [x1, y1, x2, y2] 的元素和
// 目标矩阵之和由四个相邻矩阵运算获得
return this.preSum[x2+1][y2+1] - this.preSum[x1][y2+1] - this.preSum[x2+1][y1] + this.preSum[x1][y1];
};差分数组代码模板
// 差分数组工具类
class Difference {
// 差分数组
private int[] diff;
// 输入一个初始数组,区间操作将在这个数组上进行
public Difference(int[] nums) {
assert nums.length > 0;
diff = new int[nums.length];
// 根据初始数组构造差分数组
diff[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
diff[i] = nums[i] - nums[i - 1];
}
}
// 给闭区间 [i, j] 增加 val(可以是负数)
public void increment(int i, int j, int val) {
diff[i] += val;
if (j + 1 < diff.length) {
diff[j + 1] -= val;
}
}
// 返回结果数组
public int[] result() {
int[] res = new int[diff.length];
// 根据差分数组构造结果数组
res[0] = diff[0];
for (int i = 1; i < diff.length; i++) {
res[i] = res[i - 1] + diff[i];
}
return res;
}
}// 差分数组工具类
class Difference {
// 差分数组
private:
vector<int> diff;
// 输入一个初始数组,区间操作将在这个数组上进行
public:
Difference(vector<int>& nums) {
diff = vector<int>(nums.size());
// 根据初始数组构造差分数组
diff[0] = nums[0];
for (int i = 1; i < nums.size(); i++) {
diff[i] = nums[i] - nums[i - 1];
}
}
// 给闭区间 [i, j] 增加 val(可以是负数)
void increment(int i, int j, int val) {
diff[i] += val;
if (j + 1 < diff.size()) {
diff[j + 1] -= val;
}
}
// 返回结果数组
vector<int> result() {
vector<int> res(diff.size());
// 根据差分数组构造结果数组
res[0] = diff[0];
for (int i = 1; i < diff.size(); i++) {
res[i] = res[i - 1] + diff[i];
}
return res;
}
};# 差分数组工具类
class Difference:
# 差分数组
def __init__(self, nums: List[int]):
assert len(nums) > 0
self.diff = [0] * len(nums)
# 根据初始数组构造差分数组
self.diff[0] = nums[0]
for i in range(1, len(nums)):
self.diff[i] = nums[i] - nums[i - 1]
# 给闭区间 [i, j] 增加 val(可以是负数)
def increment(self, i: int, j: int, val: int) -> None:
self.diff[i] += val
if j + 1 < len(self.diff):
self.diff[j + 1] -= val
# 返回结果数组
def result(self) -> List[int]:
res = [0] * len(self.diff)
# 根据差分数组构造结果数组
res[0] = self.diff[0]
for i in range(1, len(self.diff)):
res[i] = res[i - 1] + self.diff[i]
return res// 差分数组工具类
type Difference struct {
// 差分数组
diff []int
}
// 输入一个初始数组,区间操作将在这个数组上进行
func NewDifference(nums []int) *Difference {
diff := make([]int, len(nums))
// 根据初始数组构造差分数组
diff[0] = nums[0]
for i := 1; i < len(nums); i++ {
diff[i] = nums[i] - nums[i-1]
}
return &Difference{diff: diff}
}
// 给闭区间 [i, j] 增加 val(可以是负数)
func (d *Difference) Increment(i, j, val int) {
d.diff[i] += val
if j+1 < len(d.diff) {
d.diff[j+1] -= val
}
}
// 返回结果数组
func (d *Difference) Result() []int {
res := make([]int, len(d.diff))
// 根据差分数组构造结果数组
res[0] = d.diff[0]
for i := 1; i < len(d.diff); i++ {
res[i] = res[i-1] + d.diff[i]
}
return res
}class Difference {
constructor(nums) {
// 差分数组
this.diff = new Array(nums.length);
// 根据初始数组构造差分数组
this.diff[0] = nums[0];
for (let i = 1; i < nums.length; i++) {
this.diff[i] = nums[i] - nums[i - 1];
}
}
// 给闭区间 [i, j] 增加 val(可以是负数)
increment(i, j, val) {
this.diff[i] += val;
if (j + 1 < this.diff.length) {
this.diff[j + 1] -= val;
}
}
// 返回结果数组
result() {
let res = new Array(this.diff.length);
// 根据差分数组构造结果数组
res[0] = this.diff[0];
for (let i = 1; i < this.diff.length; i++) {
res[i] = res[i - 1] + this.diff[i];
}
return res;
}
}队列/栈
队列和栈本身是比较简单的数据结构,但是它们在算法题中的运用需要专门练习。
核心框架,建议用时 0.5 天
习题,建议用时 1~2 天
单调栈和单调队列是基于栈和队列的两种变体,它们能够解决一些特殊的问题,需要掌握。
核心框架,建议用时 1~2 天
习题,建议用时 1~2 天
二叉树 & 递归思想
所有递归算法的本质上都是二叉树的遍历,而且二叉树算法经常出现在面试/笔试中,所以二叉树章节我多放几篇文章,希望大家认真学习理解,亲自动手实践。
核心框架,建议用时 1 天
这篇核心纲领是一个总纲,主要有两部分内容:第一部分是如何在实际的算法题中理解二叉树的前中后序位置;第二部分是从二叉树的角度介绍回溯/动态规划等算法。
现在你已经了解了二叉树遍历算法,所以请认真学习第一部分。第二部分讲到的高级算法目前还没有学习,你只要有个印象就行了,等到后面学习了回溯/动态规划再回来看就会有更深的理解。
习题,建议用时 1 天
习题,建议用时 2 天
我非常强调二叉树相关算法题的重要性,因为算法的本质是穷举,树结构是所有暴力穷举算法的核心抽象。你把二叉树玩明白了,后面的高级算法都能很容易理解。
本站的 二叉树算法习题集 专门用一整个章节来练习二叉树算法,依照 二叉树算法(纲领篇) 的分类,把二叉树的习题分为三大部分:
1、递归,用「遍历」的思维模式解题。
2、递归,用「分解问题」的思维模式解题。
3、非递归,用「层序遍历」的思维模式解题。
其中「遍历」的思维模式就是后面讲的 DFS 算法、回溯算法的原型,「分解问题」的思维模式就是后面讲的动态规划、分治算法的原型,「层序遍历」就是后面讲的 BFS 算法的原型。
所以这里必须要对这几种二叉树算法进行练习。二叉树算法习题集 总量比较多,下面仅为速成读者列出难度适中且考察频率高的习题:
如果你有时间和兴趣,可以自行查看其他习题章节进行练习。
二叉搜索树
二叉搜索树是特殊的二叉树,你就记住它的特点是「左小右大」,好好利用这个特点,来优化二叉树的遍历过程。
核心框架,建议用时 1~2 天
核心框架,建议用时 1 天
数据结构设计
LRU 是经典的数据结构设计问题,必须掌握;LFU 难度更大一些,可以作为选学。
习题,建议用时 1 天
习题,建议用时 1 天
实现计算器是一个经典的数据结构设计题目,没时间的话可以把最后给出的计算器代码保存下来,如果笔试遇到字符串计算相关的题目,可以直接复制粘贴拿去用。
通用计算器代码实现
class Solution {
public int calculate(String s) {
// key 是左括号的索引,value 是对应的右括号的索引
Map<Integer, Integer> rightIndex = new HashMap<>();
// 利用栈结构来找到对应的括号
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {
stack.push(i);
} else if (s.charAt(i) == ')') {
rightIndex.put(stack.pop(), i);
}
}
return _calculate(s, 0, s.length() - 1, rightIndex);
}
// 定义:返回 s[start..end] 内的表达式的计算结果
private int _calculate(String s, int start, int end, Map<Integer, Integer> rightIndex) {
// 需要把字符串转成双端队列方便操作
Stack<Integer> stk = new Stack<>();
// 记录算式中的数字
int num = 0;
// 记录 num 前的符号,初始化为 +
char sign = '+';
for (int i = start; i <= end; i++) {
char c = s.charAt(i);
if (Character.isDigit(c)) {
num = 10 * num + (c - '0');
}
if (c == '(') {
// 递归计算括号内的表达式
num = _calculate(s, i + 1, rightIndex.get(i) - 1, rightIndex);
i = rightIndex.get(i);
}
if (c == '+' || c == '-' || c == '*' || c == '/' || i == end) {
int pre;
switch (sign) {
case '+':
stk.push(num);
break;
case '-':
stk.push(-num);
break;
// 只要拿出前一个数字做对应运算即可
case '*':
pre = stk.pop();
stk.push(pre * num);
break;
case '/':
pre = stk.pop();
stk.push(pre / num);
break;
}
// 更新符号为当前符号,数字清零
sign = c;
num = 0;
}
}
// 将栈中所有结果求和就是答案
int res = 0;
while (!stk.isEmpty()) {
res += stk.pop();
}
return res;
}
}class Solution {
public:
int calculate(string s) {
// key 是左括号的索引,value 是对应的右括号的索引
unordered_map<int, int> rightIndex;
// 利用栈结构来找到对应的括号
stack<int> stack;
for (int i = 0; i < s.length(); i++) {
if (s[i] == '(') {
stack.push(i);
} else if (s[i] == ')') {
rightIndex[stack.top()] = i;
stack.pop();
}
}
return _calculate(s, 0, s.length() - 1, rightIndex);
}
private:
// 定义:返回 s[start..end] 内的表达式的计算结果
int _calculate(string s, int start, int end, unordered_map<int, int> &rightIndex) {
// 需要把字符串转成双端队列方便操作
stack<int> stk;
// 记录算式中的数字
int num = 0;
// 记录 num 前的符号,初始化为 +
char sign = '+';
for (int i = start; i <= end; i++) {
char c = s[i];
if (isdigit(c)) {
num = 10 * num + (c - '0');
}
if (c == '(') {
// 递归计算括号内的表达式
num = _calculate(s, i + 1, rightIndex[i] - 1, rightIndex);
i = rightIndex[i];
}
if (c == '+' || c == '-' || c == '*' || c == '/' || i == end) {
int pre;
switch (sign) {
case '+':
stk.push(num);
break;
case '-':
stk.push(-num);
break;
// 只要拿出前一个数字做对应运算即可
case '*':
pre = stk.top(); stk.pop();
stk.push(pre * num);
break;
case '/':
pre = stk.top(); stk.pop();
stk.push(pre / num);
break;
}
// 更新符号为当前符号,数字清零
sign = c;
num = 0;
}
}
// 将栈中所有结果求和就是答案
int res = 0;
while (!stk.empty()) {
res += stk.top();
stk.pop();
}
return res;
}
};class Solution:
def calculate(self, s: str) -> int:
# key 是左括号的索引,value 是对应的右括号的索引
rightIndex = {}
# 利用栈结构来找到对应的括号
stack = []
for i in range(len(s)):
if s[i] == '(':
stack.append(i)
elif s[i] == ')':
rightIndex[stack.pop()] = i
return self._calculate(s, 0, len(s) - 1, rightIndex)
# 定义:返回 s[start..end] 内的表达式的计算结果
def _calculate(self, s, start, end, rightIndex):
# 需要把字符串转成双端队列方便操作
stk = []
# 记录算式中的数字
num = 0
# 记录 num 前的符号,初始化为 +
sign = '+'
i = start
while i <= end:
c = s[i]
if c.isdigit():
num = 10 * num + int(c)
if c == '(':
# 递归计算括号内的表达式
num = self._calculate(s, i + 1, rightIndex[i] - 1, rightIndex)
i = rightIndex[i]
if c in '+-*/' or i == end:
if sign == '+':
stk.append(num)
elif sign == '-':
stk.append(-num)
elif sign == '*':
pre = stk.pop()
stk.append(pre * num)
elif sign == '/':
pre = stk.pop()
stk.append(int(pre / num))
# 更新符号为当前符号,数字清零
sign = c
num = 0
i += 1
# 将栈中所有结果求和就是答案
res = 0
while stk:
res += stk.pop()
return resfunc calculate(s string) int {
// key 是左括号的索引,value 是对应的右括号的索引
rightIndex := make(map[int]int)
// 利用栈结构来找到对应的括号
stack := []int{}
for i := 0; i < len(s); i++ {
if s[i] == '(' {
stack = append(stack, i)
} else if s[i] == ')' {
pop := stack[len(stack)-1]
stack = stack[:len(stack)-1]
rightIndex[pop] = i
}
}
return _calculate(s, 0, len(s)-1, rightIndex)
}
// 定义:返回 s[start..end] 内的表达式的计算结果
func _calculate(s string, start int, end int, rightIndex map[int]int) int {
// 需要把字符串转成双端队列方便操作
stk := []int{}
// 记录算式中的数字
num := 0
// 记录 num 前的符号,初始化为 +
// 修改为 byte 类型
sign := byte('+')
for i := start; i <= end; i++ {
c := s[i]
if c >= '0' && c <= '9' {
num = 10*num + int(c-'0')
}
if c == '(' {
// 递归计算括号内的表达式
num = _calculate(s, i+1, rightIndex[i]-1, rightIndex)
i = rightIndex[i]
}
if c == '+' || c == '-' || c == '*' || c == '/' || i == end {
var pre int
switch sign {
case '+':
stk = append(stk, num)
case '-':
stk = append(stk, -num)
// 只要拿出前一个数字做对应运算即可
case '*':
pre = stk[len(stk)-1]
stk[len(stk)-1] = pre * num
case '/':
pre = stk[len(stk)-1]
stk[len(stk)-1] = pre / num
}
// 更新符号为当前符号,数字清零
sign = c
num = 0
}
}
// 将栈中所有结果求和就是答案
res := 0
for len(stk) != 0 {
res += stk[len(stk)-1]
stk = stk[:len(stk)-1]
}
return res
}var calculate = function(s) {
// key 是左括号的索引,value 是对应的右括号的索引
let rightIndex = new Map();
// 利用栈结构来找到对应的括号
let stack = [];
for (let i = 0; i < s.length; i++) {
if (s[i] === '(') {
stack.push(i);
} else if (s[i] === ')') {
rightIndex.set(stack.pop(), i);
}
}
return _calculate(s, 0, s.length - 1, rightIndex);
};
var _calculate = function(s, start, end, rightIndex) {
// 需要把字符串转成双端队列方便操作
let stk = [];
// 记录算式中的数字
let num = 0;
// 记录 num 前的符号,初始化为 +
let sign = '+';
for (let i = start; i <= end; i++) {
let c = s[i];
if (/\d/.test(c)) {
num = 10 * num + (c - '0');
}
if (c === '(') {
// 递归计算括号内的表达式
num = _calculate(s, i + 1, rightIndex.get(i) - 1, rightIndex);
i = rightIndex.get(i);
}
if ('+-*/'.includes(c) || i === end) {
let pre;
switch (sign) {
case '+':
stk.push(num);
break;
case '-':
stk.push(-num);
break;
// 只要拿出前一个数字做对应运算即可
case '*':
pre = stk.pop();
stk.push(pre * num);
break;
case '/':
pre = stk.pop();
// 修正整数除法
stk.push(Math.trunc(pre / num));
break;
}
// 更新符号为当前符号,数字清零
sign = c;
num = 0;
}
}
// 将栈中所有结果求和就是答案
let res = 0;
while (stk.length) {
res += stk.pop();
}
return res;
};习题,建议用时 1 天
图算法
环检测、拓扑排序、二分图判定是经典的图算法,本质上就是对图的遍历,并不难掌握。
核心框架,建议用时 1~2 天
Union Find 算法是比较实用的图算法,你需要了解它的原理和 API。
建议把最后给出的 UF 类提前保存下来,若笔试允许使用 IDE 则可以直接复用。
核心框架,建议用时 1 天
Union Find 代码模板
这里直接给出效率最高的路径压缩代码实现:
class UF {
// 连通分量个数
private int count;
// 存储每个节点的父节点
private int[] parent;
// n 为图中节点的个数
public UF(int n) {
this.count = n;
parent = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
// 将节点 p 和节点 q 连通
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
parent[rootQ] = rootP;
// 两个连通分量合并成一个连通分量
count--;
}
// 判断节点 p 和节点 q 是否连通
public boolean connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
public int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
// 返回图中的连通分量个数
public int count() {
return count;
}
}class UF {
private:
// 连通分量个数
int _count;
// 存储每个节点的父节点
vector<int> parent;
public:
// n 为图中节点的个数
UF(int n) {
this->_count = n;
this->parent.resize(n);
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
// 将节点 p 和节点 q 连通
void union_(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
parent[rootQ] = rootP;
// 两个连通分量合并成一个连通分量
_count--;
}
// 判断节点 p 和节点 q 是否连通
bool connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
// 返回图中的连通分量个数
int count() {
return _count;
}
};class UF:
# 连通分量个数
_count: int
# 存储每个节点的父节点
parent: List[int]
# n 为图中节点的个数
def __init__(self, n: int):
self._count = n
self.parent = [i for i in range(n)]
# 将节点 p 和节点 q 连通
def union(self, p: int, q: int):
rootP = self.find(p)
rootQ = self.find(q)
if rootP == rootQ:
return
self.parent[rootQ] = rootP
# 两个连通分量合并成一个连通分量
self._count -= 1
# 判断节点 p 和节点 q 是否连通
def connected(self, p: int, q: int) -> bool:
rootP = self.find(p)
rootQ = self.find(q)
return rootP == rootQ
def find(self, x: int) -> int:
if self.parent[x] != x:
self.parent[x] = self.find(self.parent[x])
return self.parent[x]
# 返回图中的连通分量个数
def count(self) -> int:
return self._counttype UF struct {
// 连通分量个数
count int
// 存储每个节点的父节点
parent []int
}
// n 为图中节点的个数
func NewUF(n int) *UF {
parent := make([]int, n)
for i := 0; i < n; i++ {
parent[i] = i
}
return &UF{
count: n,
parent: parent,
}
}
// 将节点 p 和节点 q 连通
func (u *UF) Union(p, q int) {
rootP := u.Find(p)
rootQ := u.Find(q)
if rootP == rootQ {
return
}
u.parent[rootQ] = rootP
// 两个连通分量合并成一个连通分量
u.count--
}
// 判断节点 p 和节点 q 是否连通
func (u *UF) Connected(p, q int) bool {
rootP := u.Find(p)
rootQ := u.Find(q)
return rootP == rootQ
}
func (u *UF) Find(x int) int {
if u.parent[x] != x {
u.parent[x] = u.Find(u.parent[x])
}
return u.parent[x]
}
// 返回图中的连通分量个数
func (u *UF) Count() int {
return u.count
}class UF {
// n 为图中节点的个数
constructor(n) {
// 连通分量个数
this._count = n
// 存储每个节点的父节点
this.parent = Array.from({ length: n }, (_, index) => index)
}
// 将节点 p 和节点 q 连通
union(p, q) {
const rootP = this.find(p)
const rootQ = this.find(q)
if (rootP === rootQ) {
return
}
this.parent[rootQ] = rootP
// 两个连通分量合并成一个连通分量
this._count--
}
// 判断节点 p 和节点 q 是否连通
connected(p, q) {
const rootP = this.find(p)
const rootQ = this.find(q)
return rootP === rootQ
}
find(x) {
if (this.parent[x] !== x) {
this.parent[x] = this.find(this.parent[x])
}
return this.parent[x]
}
// 返回图中的连通分量个数
count() {
return this._count
}
}最小生成树问题也是比较实用的图论算法,你需要了解它的定义及使用场景。
Kruskal 和 Prim 是两种经典的最小生成树算法。其中 Kruskal 算法的本质是 Union Find 算法 + 排序,相对简单,所以速成读者了解 Kruskal 算法即可。
核心框架,建议用时 1 天
Dijkstra 最短路径算法属于经典图论算法,需要掌握。它的本质就经过改良的二叉树 BFS 算法,你可以把模板保存下来,以便笔试时快速运用。
核心框架,建议用时 1 天
Dijkstra 算法模板(伪码)
class State {
// 当前节点 ID
int node;
// 从起点 s 到当前 node 节点的最小路径权重和
int distFromStart;
public State(int node, int distFromStart) {
this.node = node;
this.distFromStart = distFromStart;
}
}
// 输入不包含负权重边的加权图 graph 和起点 src
// 返回从起点 src 到其他节点的最小路径权重和
int[] dijkstra(Graph graph, int src) {
// 记录从起点 src 到其他节点的最小路径权重和
// distTo[i] 表示从起点 src 到节点 i 的最小路径权重和
int[] distTo = new int[graph.size()];
// 都初始化为正无穷,表示未计算
Arrays.fill(distTo, Integer.MAX_VALUE);
// 优先级队列,distFromStart 较小的节点排在前面
Queue<State> pq = new PriorityQueue<>((a, b) -> {
return a.distFromStart - b.distFromStart;
});
// 从起点 src 开始进行 BFS
pq.offer(new State(src, 0));
distTo[src] = 0;
while (!pq.isEmpty()) {
State state = pq.poll();
int curNode = state.node;
int curDistFromStart = state.distFromStart;
if (distTo[curNode] < curDistFromStart) {
// 在 Dijkstra 算法中,队列中可能存在重复的节点 state
// 所以要在元素出队时进行判断,去除较差的重复节点
continue;
}
for (Edge e : graph.neighbors(curNode)) {
int nextNode = e.to;
int nextDistFromStart = curDistFromStart + e.weight;
if (distTo[nextNode] <= nextDistFromStart) {
continue;
}
// 将 nextNode 节点加入优先级队列
pq.offer(new State(nextNode, nextDistFromStart));
// 记录 nextNode 节点到起点的最小路径权重和
distTo[nextNode] = nextDistFromStart;
}
}
return distTo;
}// 记录队列中的状态
struct State {
// 当前节点 ID
int node;
// 从起点 s 到当前 node 节点的最小路径权重和
int distFromStart;
State(int _node, int _distFromStart)
: node(_node), distFromStart(_distFromStart) {}
};
// 自定义比较器,使得 distFromStart 较小的 State 先出队
struct Compare {
bool operator()(const State& a, const State& b) const {
return a.distFromStart > b.distFromStart;
}
};
// 输入不包含负权重边的加权图 graph 和起点 src
// 返回从起点 src 到其他节点的最小路径权重和
std::vector<int> dijkstra(Graph& graph, int src) {
// 记录从起点 src 到其他节点的最小路径权重和
// distTo[i] 表示从起点 src 到节点 i 的最小路径权重和
std::vector<int> distTo(graph.size(), INT_MAX);
// 优先级队列,distFromStart 较小的节点排在前面
std::priority_queue<State, std::vector<State>, Compare> pq;
// 从起点 src 开始进行 BFS
pq.emplace(src, 0);
distTo[src] = 0;
while (!pq.empty()) {
State state = pq.top();
pq.pop();
int curNode = state.node;
int curDistFromStart = state.distFromStart;
if (distTo[curNode] < curDistFromStart) {
// 在 Dijkstra 算法中,队列中可能存在重复的节点 state
// 所以要在元素出队时进行判断,去除较差的重复节点
continue;
}
for (const Edge& e : graph.neighbors(curNode)) {
int nextNode = e.to;
int nextDistFromStart = curDistFromStart + e.weight;
if (distTo[nextNode] <= nextDistFromStart) {
continue;
}
// 将 nextNode 节点加入优先级队列
pq.emplace(nextNode, nextDistFromStart);
// 记录 nextNode 节点到起点的最小路径权重和
distTo[nextNode] = nextDistFromStart;
}
}
return distTo;
}import heapq
from typing import List
class State:
# 当前节点 ID
def __init__(self, node: int, distFromStart: int):
self.node = node
# 从起点 s 到当前 node 节点的最小路径权重和
self.distFromStart = distFromStart
# 定义小顶堆所需的比较函数
def __lt__(self, other: "State") -> bool:
return self.distFromStart < other.distFromStart
# 输入不包含负权重边的加权图 graph 和起点 src
# 返回从起点 src 到其他节点的最小路径权重和
def dijkstra(graph: Graph, src: int) -> List[int]:
# 记录从起点 src 到其他节点的最小路径权重和
# distTo[i] 表示从起点 src 到节点 i 的最小路径权重和
distTo: List[int] = [float('inf')] * graph.size()
# 优先级队列,distFromStart 较小的节点排在前面
pq: List[State] = []
# 从起点 src 开始进行 BFS
heapq.heappush(pq, State(src, 0))
distTo[src] = 0
while pq:
state = heapq.heappop(pq)
curNode = state.node
curDistFromStart = state.distFromStart
if distTo[curNode] < curDistFromStart:
# 在 Dijkstra 算法中,队列中可能存在重复的节点 state
# 所以要在元素出队时进行判断,去除较差的重复节点
continue
package main
import (
"container/heap"
"math"
)
// 记录队列中的状态
type State struct {
// 当前节点 ID
node int
// 从起点 s 到当前 node 节点的最小路径权重和
distFromStart int
}
// 优先级队列,distFromStart 较小的节点排在前面
type PriorityQueue []*State
func (pq PriorityQueue) Len() int { return len(pq) }
func (pq PriorityQueue) Less(i, j int) bool {
return pq[i].distFromStart < pq[j].distFromStart
}
func (pq PriorityQueue) Swap(i, j int) { pq[i], pq[j] = pq[j], pq[i] }
func (pq *PriorityQueue) Push(x interface{}) {
*pq = append(*pq, x.(*State))
}
func (pq *PriorityQueue) Pop() interface{} {
old := *pq
n := len(old)
item := old[n-1]
*pq = old[:n-1]
return item
}
// 输入不包含负权重边的加权图 graph 和起点 src
// 返回从起点 src 到其他节点的最小路径权重和
func dijkstra(graph Graph, src int) []int {
// 记录从起点 src 到其他节点的最小路径权重和
// distTo[i] 表示从起点 src 到节点 i 的最小路径权重和
distTo := make([]int, graph.Size())
// 都初始化为正无穷,表示未计算
for i := range distTo {
distTo[i] = math.MaxInt32
}
pq := &PriorityQueue{}
heap.Init(pq)
// 从起点 src 开始进行 BFS
heap.Push(pq, &State{node: src, distFromStart: 0})
distTo[src] = 0
for pq.Len() > 0 {
state := heap.Pop(pq).(*State)
curNode := state.node
curDistFromStart := state.distFromStart
if distTo[curNode] < curDistFromStart {
// 在 Dijkstra 算法中,队列中可能存在重复的节点 state
// 所以要在元素出队时进行判断,去除较差的重复节点
continue
}
for _, e := range graph.neighbors(curNode) {
nextNode := e.to
nextDistFromStart := curDistFromStart + e.weight
if distTo[nextNode] <= nextDistFromStart {
continue
}
// 将 nextNode 节点加入优先级队列
heap.Push(pq, &State{node: nextNode, distFromStart: nextDistFromStart})
// 记录 nextNode 节点到起点的最小路径权重和
distTo[nextNode] = nextDistFromStart
}
}
return distTo
}// 记录队列中的状态
class State {
// 当前节点 ID
constructor(node, distFromStart) {
this.node = node;
// 从起点 s 到当前 node 节点的最小路径权重和
this.distFromStart = distFromStart;
}
}
// 输入不包含负权重边的加权图 graph 和起点 src
// 返回从起点 src 到其他节点的最小路径权重和
function dijkstra(graph, src) {
// 记录从起点 src 到其他节点的最小路径权重和
// distTo[i] 表示从起点 src 到节点 i 的最小路径权重和
const distTo = Array(graph.size()).fill(Infinity);
// 优先级队列,distFromStart 较小的节点排在前面
const pq = new PriorityQueue((a, b) => a.distFromStart - b.distFromStart);
// 从起点 src 开始进行 BFS
pq.enqueue(new State(src, 0));
distTo[src] = 0;
while (!pq.isEmpty()) {
const state = pq.dequeue();
const curNode = state.node;
const curDistFromStart = state.distFromStart;
if (distTo[curNode] < curDistFromStart) {
// 在 Dijkstra 算法中,队列中可能存在重复的节点 state
// 所以要在元素出队时进行判断,去除较差的重复节点
continue;
}
for (const e of graph.neighbors(curNode)) {
const nextNode = e.to;
const nextDistFromStart = curDistFromStart + e.weight;
if (distTo[nextNode] <= nextDistFromStart) {
continue;
}
// 将 nextNode 节点加入优先级队列
pq.enqueue(new State(nextNode, nextDistFromStart));
// 记录 nextNode 节点到起点的最小路径权重和
distTo[nextNode] = nextDistFromStart;
}
}
return distTo;
}DFS/回溯算法
回溯算法是一种纯粹的暴力穷举算法,必须掌握。
因为笔试时是按照通过的测试用例数量来算分的,如果有些题目你实在写不出最优解,写一个回溯算法暴力穷举一下,虽然过不了所有测试用例,但是能过一部分,也能捞到一点分数。
下面列举的文章中的例题都是经典的回溯算法题目,必知必会,一定要透彻地掌握。
核心框架,建议用时 1~2 天
核心框架,建议用时 1~2 天
习题,建议用时 2 天
大部分回溯算法的本质就是排列组合,你把 回溯算法秒杀所有排列/组合/子集问题 想明白,很多回溯题目都可以直接秒。
本站的回溯算法习题章节如下:
不过习题章节的题目比较多,如果你有时间可以都看一看,时间紧的话我帮你精选几道。建议安装 Chrome 插件,在题目页面可以查看本站的思路和解法代码:
BFS 算法
BFS 也是一种暴力穷举算法,必须掌握。它的本质就是二叉树的层序遍历,适合解决最短路径问题。
核心框架,建议用时 1 天
习题,建议用时 2 天
本站的 BFS 习题章节如下:
不过这两章习题比较多,如果你有时间可以都刷完,时间紧的话我帮你精选几道做一做。建议安装 Chrome 插件,在题目页面可以查看本站的思路和解法代码:
动态规划
动态规划本质上也是暴力穷举,只不过有些问题的穷举过程中存在重叠子问题,所以可以通过备忘录进行优化,对于这类算法,我们通常称为动态规划算法。
动态规划的暴力穷举解法一般是递归形式,优化方法非常固定,要么就是添加备忘录,要么就是改写成迭代形式。
动态规划的难点在于那个暴力解(状态转移方程)怎么写,请你阅读下面的文章,尤其注意得到状态转移方程的思维过程。
核心框架,建议用时 1~2 天
核心框架,建议用时 1~2 天
习题,建议用时 1~2 天
习题,建议用时 1~2 天
贪心算法
一般的算法问题,需要暴力穷举所有解,从中找到最优解。
而有些算法问题,如果你充分利用信息,不需要用暴力穷举所有解,就能找到最优解,这就叫贪心选择性质,这种算法叫贪心算法。
所以贪心算法没有固定的套路,它的关键在于细心观察,看看是否能够充分利用信息,提前排除一些不可能是最优解的情况。
核心框架,建议用时 1 天
分治算法
有一部分算法问题,分而治之会有更高的效率,下面这篇分治算法教程所讲的例题是前面讲过的一道链表题目。
核心框架,建议用时 1 天
数学
一般笔试中数学相关算法比较少,不过一些经典的技巧还是有必要掌握。
习题,建议用时 1~2 天
其他经典面试题
这里列出一些经典算法题,它们本质上都是上面介绍的算法的运用。掌握了上面的所有算法后,一般难度的面试题你应该都能够解决了。
习题,建议用时 1~2 天
习题,建议用时 1~2 天
nSum 万能函数
// 注意:调用这个函数之前一定要先给 nums 排序
// n 填写想求的是几数之和,start 从哪个索引开始计算(一般填 0),target 填想凑出的目标和
List<List<Integer>> nSumTarget(int[] nums, int n, int start, long target) {
int sz = nums.length;
List<List<Integer>> res = new ArrayList<>();
// 至少是 2Sum,且数组大小不应该小于 n
if (n < 2 || sz < n) return res;
// 2Sum 是 base case
if (n == 2) {
// 双指针那一套操作
int lo = start, hi = sz - 1;
while (lo < hi) {
int sum = nums[lo] + nums[hi];
int left = nums[lo], right = nums[hi];
if (sum < target) {
while (lo < hi && nums[lo] == left) lo++;
} else if (sum > target) {
while (lo < hi && nums[hi] == right) hi--;
} else {
res.add(new ArrayList<>(Arrays.asList(left, right)));
while (lo < hi && nums[lo] == left) lo++;
while (lo < hi && nums[hi] == right) hi--;
}
}
} else {
// n > 2 时,递归计算 (n-1)Sum 的结果
for (int i = start; i < sz; i++) {
List<List<Integer>> sub = nSumTarget(nums, n - 1, i + 1, target - nums[i]);
for (List<Integer> arr : sub) {
// (n-1)Sum 加上 nums[i] 就是 nSum
arr.add(nums[i]);
res.add(arr);
}
while (i < sz - 1 && nums[i] == nums[i + 1]) i++;
}
}
return res;
}// 注意:调用这个函数之前一定要先给 nums 排序
// n 填写想求的是几数之和,start 从哪个索引开始计算(一般填 0),target 填想凑出的目标和
vector<vector<int>> nSumTarget(vector<int>& nums, int n, int start, long target) {
int sz = nums.size();
vector<vector<int>> res;
// 至少是 2Sum,且数组大小不应该小于 n
if (n < 2 || sz < n) return res;
// 2Sum 是 base case
if (n == 2) {
// 双指针那一套操作
int lo = start, hi = sz - 1;
while (lo < hi) {
int sum = nums[lo] + nums[hi];
int left = nums[lo], right = nums[hi];
if (sum < target) {
while (lo < hi && nums[lo] == left) lo++;
} else if (sum > target) {
while (lo < hi && nums[hi] == right) hi--;
} else {
res.push_back({left, right});
while (lo < hi && nums[lo] == left) lo++;
while (lo < hi && nums[hi] == right) hi--;
}
}
} else {
// n > 2 时,递归计算 (n-1)Sum 的结果
for (int i = start; i < sz; i++) {
vector<vector<int>> sub = nSumTarget(nums, n - 1, i + 1, target - nums[i]);
for (vector<int>& arr : sub) {
// (n-1)Sum 加上 nums[i] 就是 nSum
arr.push_back(nums[i]);
res.push_back(arr);
}
while (i < sz - 1 && nums[i] == nums[i + 1]) i++;
}
}
return res;
}# 注意:调用这个函数之前一定要先给 nums 排序
# n 填写想求的是几数之和,start 从哪个索引开始计算(一般填 0),target 填想凑出的目标和
def nSumTarget(nums: List[int], n: int, start: int, target: int) -> List[List[int]]:
sz = len(nums)
res = []
# 至少是 2Sum,且数组大小不应该小于 n
if n < 2 or sz < n:
return res
# 2Sum 是 base case
if n == 2:
# 双指针那一套操作
lo, hi = start, sz-1
while lo < hi:
sum = nums[lo] + nums[hi]
left, right = nums[lo], nums[hi]
if sum < target:
while lo < hi and nums[lo] == left:
lo += 1
elif sum > target:
while lo < hi and nums[hi] == right:
hi -= 1
else:
res.append([left, right])
while lo < hi and nums[lo] == left:
lo += 1
while lo < hi and nums[hi] == right:
hi -= 1
return res
else:
# n > 2 时,递归计算 (n-1)Sum 的结果
for i in range(start, sz):
if i > start and nums[i] == nums[i - 1]:
# 跳过重复元素
continue
subs = nSumTarget(nums, n-1, i+1, target-nums[i])
for sub in subs:
# (n-1)Sum 加上 nums[i] 就是 nSum
sub.append(nums[i])
res.append(sub)
return res// 注意:调用这个函数之前一定要先给 nums 排序
// n 填写想求的是几数之和,start 从哪个索引开始计算(一般填 0),target 填想凑出的目标和
func nSumTarget(nums []int, n int, start int, target int64) [][]int {
sz := len(nums)
res := [][]int{}
// 至少是 2Sum,且数组大小不应该小于 n
if n < 2 || sz < n {
return res
}
// 2Sum 是 base case
if n == 2 {
// 双指针那一套操作
lo, hi := start, sz-1
for lo < hi {
sum := nums[lo] + nums[hi]
left, right := nums[lo], nums[hi]
if int64(sum) < target {
for lo < hi && nums[lo] == left {
lo++
}
} else if int64(sum) > target {
for lo < hi && nums[hi] == right {
hi--
}
} else {
res = append(res, []int{left, right})
for lo < hi && nums[lo] == left {
lo++
}
for lo < hi && nums[hi] == right {
hi--
}
}
}
} else {
// n > 2 时,递归计算 (n-1)Sum 的结果
for i := start; i < sz; i++ {
subs := nSumTarget(nums, n-1, i+1, target-int64(nums[i]))
for _, sub := range subs {
// (n-1)Sum 加上 nums[i] 就是 nSum
sub = append(sub, nums[i])
res = append(res, sub)
}
for i < sz-1 && nums[i] == nums[i+1] {
i++
}
}
}
return res
}// 注意:调用这个函数之前一定要先给 nums 排序
// n 填写想求的是几数之和,start 从哪个索引开始计算(一般填 0),target 填想凑出的目标和
var nSumTarget = function(nums, n, start, target) {
let sz = nums.length;
let res = [];
// 至少是 2Sum,且数组大小不应该小于 n
if (n < 2 || sz < n) return res;
// 2Sum 是 base case
if (n == 2) {
// 双指针那一套操作
let lo = start, hi = sz - 1;
while (lo < hi) {
let sum = nums[lo] + nums[hi];
let left = nums[lo], right = nums[hi];
if (sum < target) {
while (lo < hi && nums[lo] == left) lo++;
} else if (sum > target) {
while (lo < hi && nums[hi] == right) hi--;
} else {
res.push([left, right]);
while (lo < hi && nums[lo] == left) lo++;
while (lo < hi && nums[hi] == right) hi--;
}
}
// n > 2 时,递归计算 (n-1)Sum 的结果
} else {
for (let i = start; i < sz; i++) {
let sub = nSumTarget(nums, n - 1, i + 1, target - nums[i]);
for (let arr of sub) {
// (n-1)Sum 加上 nums[i] 就是 nSum
arr.push(nums[i]);
res.push(arr);
}
while (i < sz - 1 && nums[i] == nums[i + 1]) i++;
}
}
return res;
}排序算法
在笔试和面试中,一般不会出现排序算法的题目让你写代码;但是在面试中可能会问到经典排序算法的原理、时间复杂度和适用场景,所以你需要对十大经典排序算法有所了解。
排序算法串讲,建议用时 1 天
建议观看 十大排序算法导读 中的视频,了解十大排序算法的核心原理、复杂度分析和适用场景。