如何高效解决接雨水问题

labuladong原创约 2116 字

本文讲解的例题

LeetCode	力扣	难度
11. Container With Most Water	11. 盛最多水的容器	🟠
42. Trapping Rain Water	42. 接雨水	🔴

前置知识

阅读本文前，你需要先学习：

力扣第 42 题「接雨水」挺有意思，在面试题中出现频率还挺高的，本文就来步步优化，讲解一下这道题。

先看一下题目：

42. 接雨水 | 力扣 | LeetCode |

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

就是用一个数组表示一个条形图，问你这个条形图最多能接多少水。

java 🟢

int trap(int[] height);

cpp 🤖

int trap(vector<int>& height);

python 🤖

def trap(height: List[int]) -> int:

go 🤖

func trap(height []int) int {}

javascript 🤖

 var trap = function(height) {}

下面就来由浅入深介绍暴力解法 -> 备忘录解法 -> 双指针解法，在 O(N) 时间 O(1) 空间内解决这个问题。

一、核心思路

小技巧

做算法题，如果对题目提出的问题没有思路，不妨尝试化简问题，先从局部思考，先写出最简单粗暴的解法，也许会有突破点。逐步优化后也许就能找到最优解。

比如这道题，先不考虑整个柱状图能装多少水，仅仅考虑位置 i 这一个位置能装下多少水？

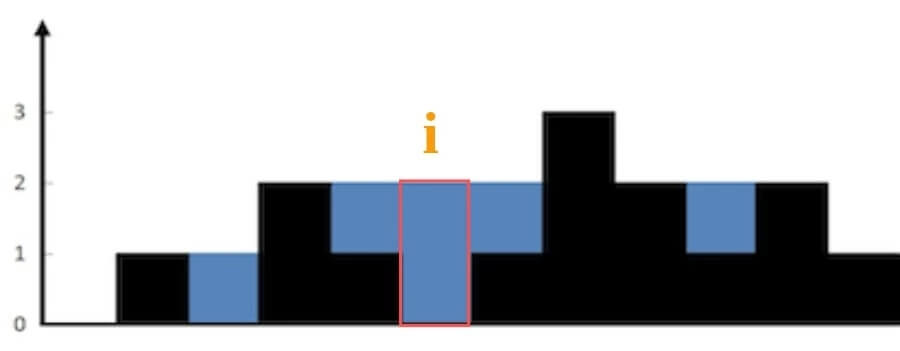
能装 2 格水，因为 height[i] 的高度为 0，而这里最多能盛 2 格水，2-0=2。

为什么位置 i 最多能盛 2 格水呢？因为，位置 i 能达到的水柱高度和其左边的最高柱子、右边的最高柱子有关，我们分别称这两个柱子高度为 l_max 和 r_max；位置 i 最大的水柱高度就是 min(l_max, r_max)。

也就是说，对于位置 i，能够装的水为：