如何判定完美矩形
本文讲解的例题
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 391. Perfect Rectangle | 391. 完美矩形 | 🔴 |
今天讲一道非常有意思,而且比较有难度的题目。
我们知道一个矩形有四个顶点,但是只要两个顶点的坐标就可以确定一个矩形了(比如左下角和右上角两个顶点坐标)。
今天来看看力扣第 391 题「完美矩形」,题目会给我们输入一个数组 rectangles,里面装着若干四元组 (x1,y1,x2,y2),每个四元组就是记录一个矩形的左下角和右上角坐标。
391. 完美矩形 | 力扣 | LeetCode | 🔴
给你一个数组 rectangles ,其中 rectangles[i] = [xi, yi, ai, bi] 表示一个坐标轴平行的矩形。这个矩形的左下顶点是 (xi, yi) ,右上顶点是 (ai, bi) 。
如果所有矩形一起精确覆盖了某个矩形区域,则返回 true ;否则,返回 false 。
示例 1:
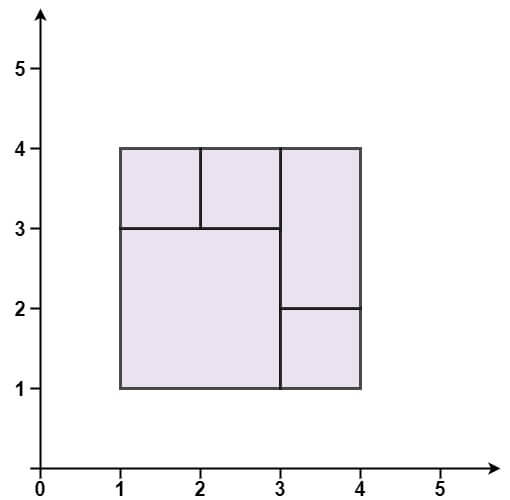
输入:rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]] 输出:true 解释:5 个矩形一起可以精确地覆盖一个矩形区域。
示例 2:
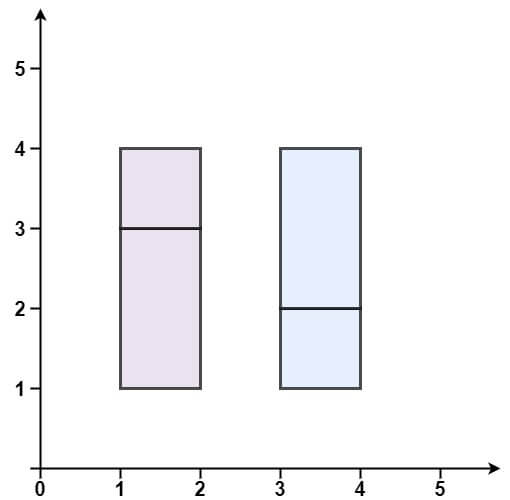
输入:rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]] 输出:false 解释:两个矩形之间有间隔,无法覆盖成一个矩形。
示例 3:
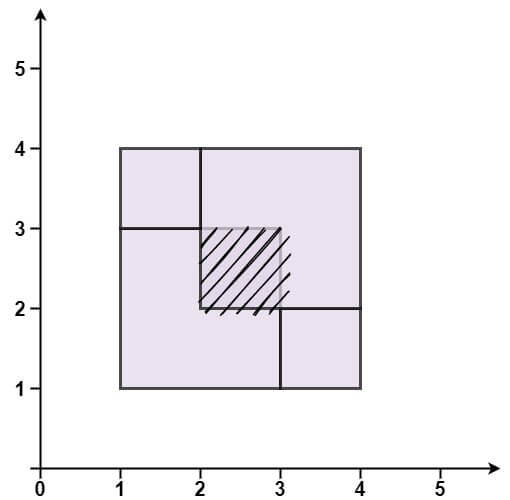
输入:rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]] 输出:false 解释:因为中间有相交区域,虽然形成了矩形,但不是精确覆盖。
提示:
1 <= rectangles.length <= 2 * 104rectangles[i].length == 4-105 <= xi, yi, ai, bi <= 105
也就是说,输入的 rectangles 数组实际上就是很多小矩形,题目要求我们输出一个布尔值,判断这些小矩形能否构成一个「完美矩形」。函数签名如下:
boolean isRectangleCover(int[][] rectangles)bool isRectangleCover(vector<vector<int>>& rectangles)def isRectangleCover(rectangles: List[List[int]]) -> boolfunc isRectangleCover(rectangles [][]int) bool {}function isRectangleCover(rectangles) {}所谓「完美矩形」,就是说 rectangles 中的小矩形拼成图形必须是一个大矩形,且大矩形中不能有重叠和空缺。
这个题目难度是 Hard,如果没有做过类似的题目,还真做不出来。
常规的思路,起码要把最终形成的图形表示出来吧,而且你要有方法去判断两个矩形是否有重叠,是否有空隙,虽然可以做到,不过感觉异常复杂。
其实,想判断最终形成的图形是否是完美矩形,需要从「面积」和「顶点」两个角度来处理。
先说说什么叫从「面积」的角度。
rectangles 数组中每个元素都是一个四元组 (x1, y1, x2, y2),表示一个小矩形的左下角顶点坐标和右上角顶点坐标。
那么假设这些小矩形最终形成了一个「完美矩形」,你会不会求这个完美矩形的左下角顶点坐标 (X1, Y1) 和右上角顶点的坐标 (X2, Y2)?
这个很简单吧,左下角顶点 (X1, Y1) 就是 rectangles 中所有小矩形中最靠左下角的那个小矩形的左下角顶点;右上角顶点 (X2, Y2) 就是所有小矩形中最靠右上角的那个小矩形的右上角顶点。
注意我们用小写字母表示小矩形的坐标,大写字母表示最终形成的完美矩形的坐标,可以这样写代码:
// 左下角顶点,初始化为正无穷,以便记录最小值
double X1 = Double.POSITIVE_INFINITY, Y1 = Double.POSITIVE_INFINITY;
// 右上角顶点,初始化为负无穷,以便记录最大值
double X2 = Double.NEGATIVE_INFINITY, Y2 = Double.NEGATIVE_INFINITY;
for(int[] rectangle : rectangles){
int x1 = rectangle[0], y1 = rectangle[1], x2 = rectangle[2], y2 = rectangle[3];
// 取小矩形左下角顶点的最小值
X1 = Math.min(X1, x1);
Y1 = Math.min(Y1, y1);
// 取小矩形右上角顶点的最大值
X2 = Math.max(X2, x2);
Y2 = Math.max(Y2, y2);
}// 左下角顶点,初始化为正无穷,以便记录最小值
int X1 = INT_MAX, Y1 = INT_MAX;
// 右上角顶点,初始化为负无穷,以便记录最大值
int X2 = INT_MIN, Y2 = INT_MIN;
for(auto &rectangle : rectangles) {
int x1 = rectangle[0], y1 = rectangle[1], x2 = rectangle[2], y2 = rectangle[3];
// 取小矩形左下角顶点的最小值
X1 = min(X1, x1); Y1 = min(Y1, y1);
// 取小矩形右上角顶点的最大值
X2 = max(X2, x2); Y2 = max(Y2, y2);
}# 左下角顶点,初始化为正无穷,以便记录最小值
X1, Y1 = inf, inf
# 右上角顶点,初始化为负无穷,以便记录最大值
X2, Y2 = -inf, -inf
for x1, y1, x2, y2 in rectangles:
# 取小矩形左下角顶点的最小值
X1, Y1 = min(X1, x1), min(Y1, y1)
# 取小矩形右上角顶点的最大值
X2, Y2 = max(X2, x2), max(Y2, y2)// 左下角顶点,初始化为正无穷,以便记录最小值
var X1, Y1 float64 = math.MaxFloat64, math.MaxFloat64
// 右上角顶点,初始化为负无穷,以便记录最大值
var X2, Y2 float64 = math.SmallestNonzeroFloat64, math.SmallestNonzeroFloat64
for _, rectangle := range rectangles {
x1, y1, x2, y2 := rectangle[0], rectangle[1], rectangle[2], rectangle[3]
// 取小矩形左下角顶点的最小值
X1, Y1 = math.Min(X1, x1), math.Min(Y1, y1)
// 取小矩形右上角顶点的最大值
X2, Y2 = math.Max(X2, x2), math.Max(Y2, y2)
}// 左下角顶点,初始化为正无穷,以便记录最小值
var X1 = Number.POSITIVE_INFINITY, Y1 = Number.POSITIVE_INFINITY;
// 右上角顶点,初始化为负无穷,以便记录最大值
var X2 = Number.NEGATIVE_INFINITY, Y2 = Number.NEGATIVE_INFINITY;
for (let i = 0; i < rectangles.length; i++) {
let rectangle = rectangles[i];
// 取小矩形左下角顶点的最小值
X1 = Math.min(X1, rectangle[0]);
Y1 = Math.min(Y1, rectangle[1]);
// 取小矩形右上角顶点的最大值
X2 = Math.max(X2, rectangle[2]);
Y2 = Math.max(Y2, rectangle[3]);
}这样就能求出完美矩形的左下角顶点坐标 (X1, Y1) 和右上角顶点的坐标 (X2, Y2) 了。
计算出的 X1,Y1,X2,Y2 坐标是完美矩形的「理论坐标」,如果所有小矩形的面积之和不等于这个完美矩形的理论面积,那么说明最终形成的图形肯定存在空缺或者重叠,肯定不是完美矩形。
代码可以进一步:
boolean isRectangleCover(int[][] rectangles) {
int X1 = Integer.MAX_VALUE, Y1 = Integer.MAX_VALUE;
int X2 = Integer.MIN_VALUE, Y2 = Integer.MIN_VALUE;
// 记录所有小矩形的面积之和
int actualArea = 0;
for (int[] rect : rectangles) {
int x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
// 计算完美矩形的理论坐标
X1 = Math.min(X1, x1);
Y1 = Math.min(Y1, y1);
X2 = Math.max(X2, x2);
Y2 = Math.max(Y2, y2);
// 累加所有小矩形的面积
actualArea += (x2 - x1) * (y2 - y1);
}
// 计算完美矩形的理论面积
int expectedArea = (X2 - X1) * (Y2 - Y1);
// 面积应该相同
if (actualArea != expectedArea) {
return false;
}
return true;
}bool isRectangleCover(vector<vector<int>>& rectangles) {
int X1 = numeric_limits<int>::max(), Y1 = numeric_limits<int>::max();
int X2 = numeric_limits<int>::min(), Y2 = numeric_limits<int>::min();
// 记录所有小矩形的面积之和
int actualArea = 0;
for (vector<int>& rect : rectangles) {
int x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
// 计算完美矩形的理论坐标
X1 = min(X1, x1);
Y1 = min(Y1, y1);
X2 = max(X2, x2);
Y2 = max(Y2, y2);
// 累加所有小矩形的面积
actualArea += (x2 - x1) * (y2 - y1);
}
// 计算完美矩形的理论面积
int expectedArea = (X2 - X1) * (Y2 - Y1);
// 面积应该相同
if (actualArea != expectedArea) {
return false;
}
return true;
}def isRectangleCover(rectangles):
X1, Y1 = float('inf'), float('inf')
X2, Y2 = float('-inf'), float('-inf')
# 记录所有小矩形的面积之和
actualArea = 0
for rect in rectangles:
x1, y1, x2, y2 = rect
# 计算完美矩形的理论坐标
X1 = min(X1, x1)
Y1 = min(Y1, y1)
X2 = max(X2, x2)
Y2 = max(Y2, y2)
# 累加所有小矩形的面积
actualArea += (x2 - x1) * (y2 - y1)
# 计算完美矩形的理论面积
expectedArea = (X2 - X1) * (Y2 - Y1)
# 面积应该相同
if actualArea != expectedArea:
return False
return Truefunc isRectangleCover(rectangles [][]int) bool {
X1, Y1, X2, Y2 := math.MaxInt64, math.MaxInt64, math.MinInt64, math.MinInt64
// 记录所有小矩形的面积之和
actualArea := 0
for _, rect := range rectangles {
x1, y1, x2, y2 := rect[0], rect[1], rect[2], rect[3]
// 计算完美矩形的理论坐标
X1 = min(X1, x1)
Y1 = min(Y1, y1)
X2 = max(X2, x2)
Y2 = max(Y2, y2)
// 累加所有小矩形的面积
actualArea += (x2 - x1) * (y2 - y1)
}
// 计算完美矩形的理论面积
expectedArea := (X2 - X1) * (Y2 - Y1)
// 面积应该相同
if actualArea != expectedArea {
return false
}
return true
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func min(a, b int) int {
if a < b {
return a
}
return b
}var isRectangleCover = function(rectangles) {
var X1 = Number.MAX_VALUE, Y1 = Number.MAX_VALUE;
var X2 = Number.MIN_VALUE, Y2 = Number.MIN_VALUE;
// 记录所有小矩形的面积之和
var actualArea = 0;
for (var rect of rectangles) {
var x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
// 计算完美矩形的理论坐标
X1 = Math.min(X1, x1);
Y1 = Math.min(Y1, y1);
X2 = Math.max(X2, x2);
Y2 = Math.max(Y2, y2);
// 累加所有小矩形的面积
actualArea += (x2 - x1) * (y2 - y1);
}
// 计算完美矩形的理论面积
var expectedArea = (X2 - X1) * (Y2 - Y1);
// 面积应该相同
if (actualArea !== expectedArea) {
return false;
}
return true;
}这样,「面积」这个维度就完成了,思路其实不难,无非就是假设最终形成的图形是个完美矩形,然后比较面积是否相等,如果不相等的话说明最终形成的图形一定存在空缺或者重叠部分,不是完美矩形。
但是反过来说,如果面积相同,是否可以证明最终形成的图形是完美矩形,一定不存在空缺或者重叠?
肯定是不行的,举个很简单的例子,你假想一个完美矩形,然后我在它中间挖掉一个小矩形,把这个小矩形向下平移一个单位。这样小矩形的面积之和没变,但是原来的完美矩形中就空缺了一部分,也重叠了一部分,已经不是完美矩形了。
综上,即便面积相同,并不能完全保证不存在空缺或者重叠,所以我们需要从「顶点」的维度来辅助判断。
记得小学的时候有一道智力题,给你一个矩形,切一刀,剩下的图形有几个顶点?答案是,如果沿着对角线切,就剩 3 个顶点;如果横着或者竖着切,剩 4 个顶点;如果只切掉一个小角,那么会出现 5 个顶点。
回到这道题,我们接下来的分析也有那么一点智力题的味道。
显然,完美矩形一定只有四个顶点。矩形嘛,按理说应该有四个顶点,如果存在空缺或者重叠的话,肯定不是四个顶点,比如说题目的这两个例子就有不止 4 个顶点:
Note
我也不知道应该用「顶点」还是「角」来形容,好像都不太准确,本文统一用「顶点」来形容,大家理解就好~
只要我们想办法计算 rectangles 中的小矩形最终形成的图形有几个顶点,就能判断最终的图形是不是一个完美矩形了。
那么顶点是如何形成的呢?我们倒是一眼就可以看出来顶点在哪里,问题是如何让计算机,让算法知道某一个点是不是顶点呢?这也是本题的难点所在。
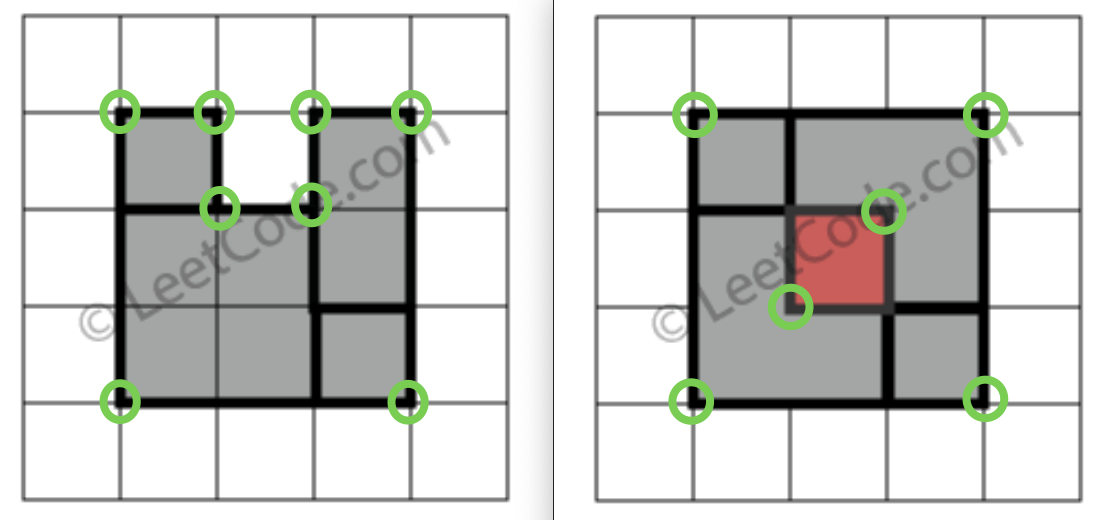
看下图的四种情况:
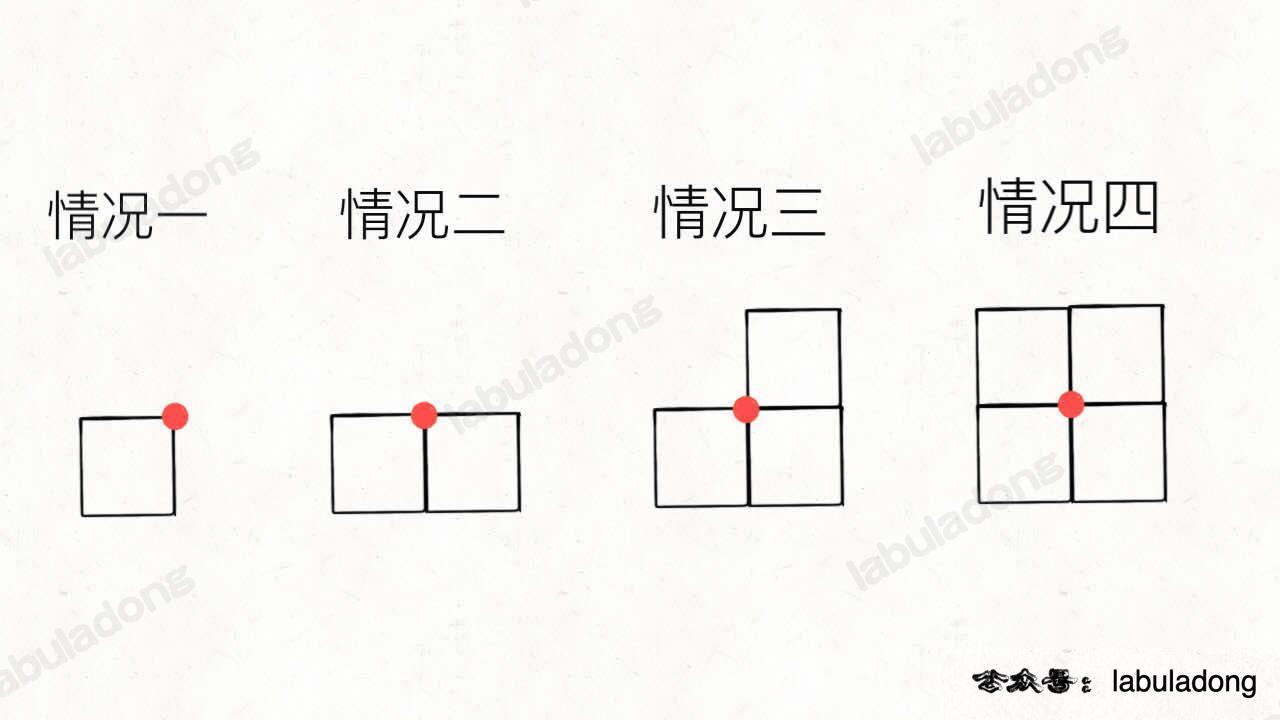
图中画红点的地方,什么时候是顶点,什么时候不是顶点?显然,情况一和情况三的时候是顶点,而情况二和情况四的时候不是顶点。
也就是说,当某一个点同时是 2 个或者 4 个小矩形的顶点时,该点最终不是顶点;当某一个点同时是 1 个或者 3 个小矩形的顶点时,该点最终是一个顶点。
注意,2 和 4 都是偶数,1 和 3 都是奇数,我们想计算最终形成的图形中有几个顶点,也就是要筛选出那些出现了奇数次的顶点,可以这样写代码:
boolean isRectangleCover(int[][] rectangles) {
int X1 = Integer.MAX_VALUE, Y1 = Integer.MAX_VALUE;
int X2 = Integer.MIN_VALUE, Y2 = Integer.MIN_VALUE;
int actualArea = 0;
// 哈希集合,记录最终图形的顶点
Set<String> points = new HashSet<>();
for (int[] rect : rectangles) {
int x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
X1 = Math.min(X1, x1);
Y1 = Math.min(Y1, y1);
X2 = Math.max(X2, x2);
Y2 = Math.max(Y2, y2);
actualArea += (x2 - x1) * (y2 - y1);
// 先算出小矩形每个点的坐标,用字符串表示,方便存入哈希集合
String p1 = x1 + "," + y1;
String p2 = x1 + "," + y2;
String p3 = x2 + "," + y1;
String p4 = x2 + "," + y2;
// 对于每个点,如果存在集合中,删除它;
// 如果不存在集合中,添加它;
// 在集合中剩下的点都是出现奇数次的点
for (String p : new String[]{p1, p2, p3, p4}) {
if (points.contains(p)) {
points.remove(p);
} else {
points.add(p);
}
}
}
int expectedArea = (X2 - X1) * (Y2 - Y1);
if (actualArea != expectedArea) {
return false;
}
// 检查顶点个数
if (points.size() != 4 ||
!points.contains(X1 + "," + Y1) ||
!points.contains(X1 + "," + Y2) ||
!points.contains(X2 + "," + Y1) ||
!points.contains(X2 + "," + Y2)) {
return false;
}
return true;
}bool isRectangleCover(vector<vector<int>>& rectangles) {
int X1 = INT_MAX, Y1 = INT_MAX;
int X2 = INT_MIN, Y2 = INT_MIN;
int actualArea = 0;
// 哈希集合,记录最终图形的顶点
unordered_set<string> points;
for (auto &rect : rectangles) {
int x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
X1 = min(X1, x1);
Y1 = min(Y1, y1);
X2 = max(X2, x2);
Y2 = max(Y2, y2);
actualArea += (x2 - x1) * (y2 - y1);
// 先算出小矩形每个点的坐标,用字符串表示,方便存入哈希集合
string p1 = to_string(x1) + "," + to_string(y1);
string p2 = to_string(x1) + "," + to_string(y2);
string p3 = to_string(x2) + "," + to_string(y1);
string p4 = to_string(x2) + "," + to_string(y2);
vector<string> pointArr = {p1, p2, p3, p4};
// 对于每个点,如果存在集合中,删除它;
// 如果不存在集合中,添加它;
// 在集合中剩下的点都是出现奇数次的点
for (auto &p : pointArr) {
if (points.count(p)) {
points.erase(p);
} else {
points.insert(p);
}
}
}
int expectedArea = (X2 - X1) * (Y2 - Y1);
if (actualArea != expectedArea) {
return false;
}
// 检查顶点个数
if (points.size() != 4 ||
!points.count(to_string(X1) + "," + to_string(Y1)) ||
!points.count(to_string(X1) + "," + to_string(Y2)) ||
!points.count(to_string(X2) + "," + to_string(Y1)) ||
!points.count(to_string(X2) + "," + to_string(Y2))) {
return false;
}
return true;
}def isRectangleCover(rectangles):
X1, Y1, X2, Y2 = float('inf'), float('inf'), float('-inf'), float('-inf')
actualArea = 0
# 哈希集合,记录最终图形的顶点
points = set()
for rect in rectangles:
x1, y1, x2, y2 = rect
X1 = min(X1, x1)
Y1 = min(Y1, y1)
X2 = max(X2, x2)
Y2 = max(Y2, y2)
actualArea += (x2 - x1) * (y2 - y1)
# 先算出小矩形每个点的坐标,用字符串表示,方便存入哈希集合
p1 = str(x1) + "," + str(y1)
p2 = str(x1) + "," + str(y2)
p3 = str(x2) + "," + str(y1)
p4 = str(x2) + "," + str(y2)
pointArr = [p1, p2, p3, p4]
# 对于每个点,如果存在集合中,删除它;
for p in pointArr:
if p in points:
points.remove(p)
else:
points.add(p)
# 如果不存在集合中,添加它;
# 在集合中剩下的点都是出现奇数次的点
expectedArea = (X2 - X1) * (Y2 - Y1)
if actualArea != expectedArea:
return False
# 检查顶点个数
if len(points) != 4 or \
str(X1) + "," + str(Y1) not in points or \
str(X1) + "," + str(Y2) not in points or \
str(X2) + "," + str(Y1) not in points or \
str(X2) + "," + str(Y2) not in points:
return False
return Truefunc isRectangleCover(rectangles [][]int) bool {
X1, Y1 := math.MaxInt32, math.MaxInt32
X2, Y2 := math.MinInt32, math.MinInt32
var actualArea int
// 哈希集合,记录最终图形的顶点
points := map[string]bool{}
for _, rect := range rectangles{
x1 := rect[0]
y1 := rect[1]
x2 := rect[2]
y2 := rect[3]
X1 = int(math.Min(float64(X1), float64(x1)))
Y1 = int(math.Min(float64(Y1), float64(y1)))
X2 = int(math.Max(float64(X2), float64(x2)))
Y2 = int(math.Max(float64(Y2), float64(y2)))
// 计算小矩形的面积
actualArea += (x2 - x1) * (y2 - y1)
// 先算出小矩形每个点的坐标,用字符串表示,方便存入哈希集合
p1 := fmt.Sprintf("%d,%d", x1, y1)
p2 := fmt.Sprintf("%d,%d", x1, y2)
p3 := fmt.Sprintf("%d,%d", x2, y1)
p4 := fmt.Sprintf("%d,%d", x2, y2)
pointArr := []string{p1, p2, p3, p4}
// 对于每个点,如果存在集合中,删除它;
// 如果不存在集合中,添加它;
// 在集合中剩下的点都是出现奇数次的点
for _, p := range pointArr{
if _, exists := points[p]; exists{
delete(points, p)
} else {
points[p] = true
}
}
}
expectedArea := (X2 - X1) * (Y2 - Y1)
if actualArea != expectedArea {
return false
}
// 检查顶点个数
if len(points) != 4 {
return false
}
if _, ex := points[fmt.Sprintf("%d,%d", X1, Y1)];!ex{
return false
}
if _, ex := points[fmt.Sprintf("%d,%d", X1, Y2)];!ex{
return false
}
if _, ex := points[fmt.Sprintf("%d,%d", X2, Y1)];!ex{
return false
}
if _, ex := points[fmt.Sprintf("%d,%d", X2, Y2)];!ex{
return false
}
return true
}var isRectangleCover = function(rectangles) {
var X1 = Number.MAX_VALUE, Y1 = Number.MAX_VALUE;
var X2 = Number.MIN_VALUE, Y2 = Number.MIN_VALUE;
var actualArea = 0;
// 哈希集合,记录最终图形的顶点
var points = new Set();
for (var rect of rectangles) {
var x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
X1 = Math.min(X1, x1);
Y1 = Math.min(Y1, y1);
X2 = Math.max(X2, x2);
Y2 = Math.max(Y2, y2);
actualArea += (x2 - x1) * (y2 - y1);
// 先算出小矩形每个点的坐标,用字符串表示,方便存入哈希集合
var p1 = x1 + "," + y1;
var p2 = x1 + "," + y2;
var p3 = x2 + "," + y1;
var p4 = x2 + "," + y2;
// 对于每个点,如果存在集合中,删除它;
// 如果不存在集合中,添加它;
// 在集合中剩下的点都是出现奇数次的点
for (var p of [p1, p2, p3, p4]) {
if (points.has(p)) {
points.delete(p);
} else {
points.add(p);
}
}
}
var expectedArea = (X2 - X1) * (Y2 - Y1);
if (actualArea !== expectedArea) {
return false;
}
// 检查顶点个数
if (points.size != 4 ||
!points.has(X1 + "," + Y1) ||
!points.has(X1 + "," + Y2) ||
!points.has(X2 + "," + Y1) ||
!points.has(X2 + "," + Y2)) {
return false;
}
return true;
};这段代码中,我们用一个 points 集合记录 rectangles 中小矩形组成的最终图形的顶点坐标,关键逻辑在于如何向 points 中添加坐标:
如果某一个顶点 p 存在于集合 points 中,则将它删除;如果不存在于集合 points 中,则将它插入。
这个简单的逻辑,让 points 集合最终只会留下那些出现了 1 次或者 3 次的顶点,那些出现了 2 次或者 4 次的顶点都被消掉了。
那么首先想到,points 集合中最后应该只有 4 个顶点对吧,如果 len(points) != 4 说明最终构成的图形肯定不是完美矩形。
但是如果 len(points) == 4 是否能说明最终构成的图形肯定是完美矩形呢?也不行,因为题目并没有说 rectangles 中的小矩形不存在重复,比如下面这种情况:
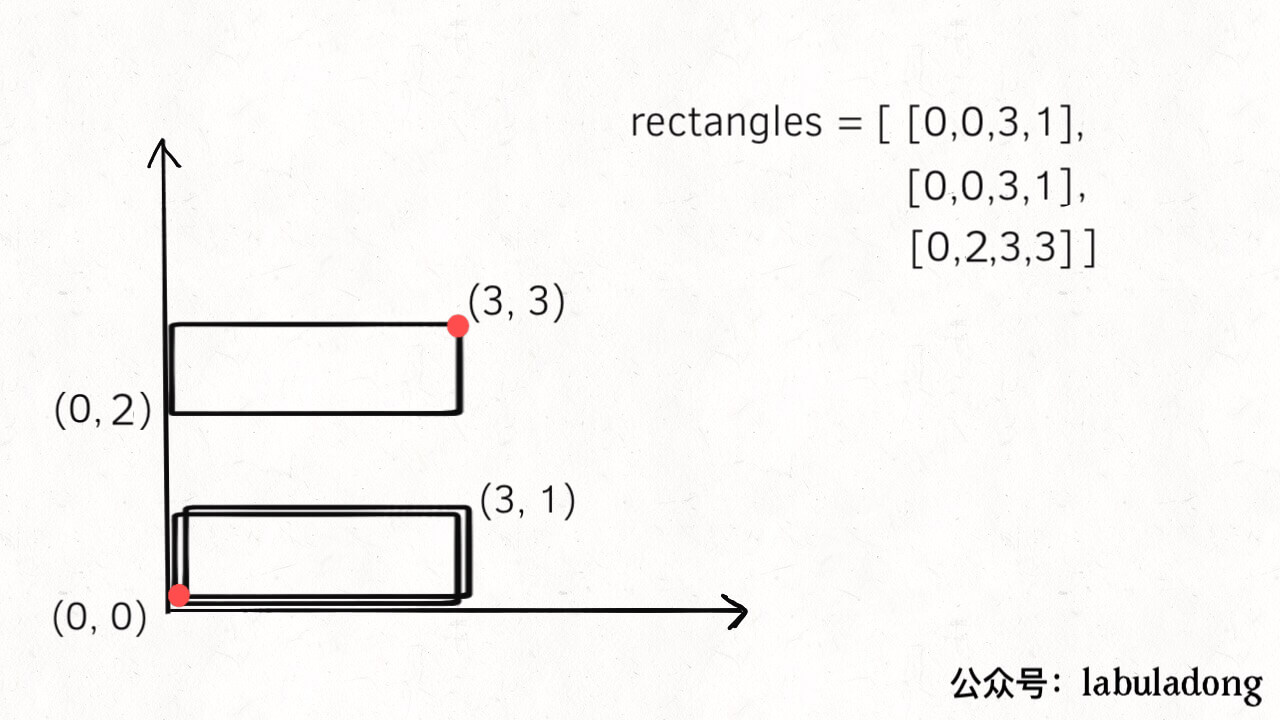
下面两个矩形重复了,按照我们的算法逻辑,它们的顶点都被消掉了,最终是剩下了四个顶点;再看面积,完美矩形的理论坐标是图中红色的点,计算出的理论面积和实际面积也相同。但是显然这种情况不是题目要求完美矩形。
所以不仅要保证 len(points) == 4,而且要保证 points 中最终剩下的点坐标就是完美矩形的四个理论坐标,直接看代码吧:
class Solution {
public boolean isRectangleCover(int[][] rectangles) {
int X1 = Integer.MAX_VALUE, Y1 = Integer.MAX_VALUE;
int X2 = Integer.MIN_VALUE, Y2 = Integer.MIN_VALUE;
Set<String> points = new HashSet<>();
int actualArea = 0;
for (int[] rect : rectangles) {
int x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
// 计算完美矩形的理论顶点坐标
X1 = Math.min(X1, x1);
Y1 = Math.min(Y1, y1);
X2 = Math.max(X2, x2);
Y2 = Math.max(Y2, y2);
// 累加小矩形的面积
actualArea += (x2 - x1) * (y2 - y1);
// 记录最终形成的图形中的顶点
String p1 = x1 + "," + y1;
String p2 = x1 + "," + y2;
String p3 = x2 + "," + y1;
String p4 = x2 + "," + y2;
for (String p : new String[]{p1, p2, p3, p4}) {
if (points.contains(p)) points.remove(p);
else points.add(p);
}
}
// 判断面积是否相同
int expectedArea = (X2 - X1) * (Y2 - Y1);
if (actualArea != expectedArea) {
return false;
}
// 判断最终留下的顶点个数是否为 4
if (points.size() != 4) {
return false;
}
// 判断留下的 4 个顶点是否是完美矩形的顶点
if (!points.contains(X1 + "," + Y1)) return false;
if (!points.contains(X1 + "," + Y2)) return false;
if (!points.contains(X2 + "," + Y1)) return false;
if (!points.contains(X2 + "," + Y2)) return false;
// 面积和顶点都对应,说明矩形符合题意
return true;
}
}#include <vector>
#include <set>
#include <climits>
#include <string>
#include <algorithm>
using namespace std;
class Solution {
public:
bool isRectangleCover(vector<vector<int>>& rectangles) {
int X1 = INT_MAX, Y1 = INT_MAX;
int X2 = INT_MIN, Y2 = INT_MIN;
set<string> points;
long long actualArea = 0; // Change type to long long to avoid overflow
for (const auto& rect : rectangles) {
int x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
// 计算完美矩形的理论顶点坐标
X1 = min(X1, x1);
Y1 = min(Y1, y1);
X2 = max(X2, x2);
Y2 = max(Y2, y2);
// 累加小矩形的面积
actualArea += static_cast<long long>(x2 - x1) * (y2 - y1); // Cast to long long before multiplication
// 记录最终形成的图形中的顶点
string p1 = to_string(x1) + "," + to_string(y1);
string p2 = to_string(x1) + "," + to_string(y2);
string p3 = to_string(x2) + "," + to_string(y1);
string p4 = to_string(x2) + "," + to_string(y2);
for (const auto& p : {p1, p2, p3, p4}) {
if (points.count(p)) points.erase(p);
else points.insert(p);
}
}
// 判断面积是否相同
long long expectedArea = static_cast<long long>(X2 - X1) * (Y2 - Y1); // Cast to long long before multiplication
if (actualArea != expectedArea) {
return false;
}
// 判断最终留下的顶点个数是否为 4
if (points.size() != 4) {
return false;
}
// 判断留下的 4 个顶点是否是完美矩形的顶点
if (!points.count(to_string(X1) + "," + to_string(Y1))) return false;
if (!points.count(to_string(X1) + "," + to_string(Y2))) return false;
if (!points.count(to_string(X2) + "," + to_string(Y1))) return false;
if (!points.count(to_string(X2) + "," + to_string(Y2))) return false;
// 面积和顶点都对应,说明矩形符合题意
return true;
}
};class Solution:
def isRectangleCover(self, rectangles: List[List[int]]) -> bool:
X1, Y1 = float('inf'), float('inf')
X2, Y2 = float('-inf'), float('-inf')
points = set()
actualArea = 0
for rect in rectangles:
x1, y1, x2, y2 = rect
# 计算完美矩形的理论顶点坐标
X1 = min(X1, x1)
Y1 = min(Y1, y1)
X2 = max(X2, x2)
Y2 = max(Y2, y2)
# 累加小矩形的面积
actualArea += (x2 - x1) * (y2 - y1)
# 记录最终形成的图形中的顶点
p1 = f"{x1},{y1}"
p2 = f"{x1},{y2}"
p3 = f"{x2},{y1}"
p4 = f"{x2},{y2}"
for p in [p1, p2, p3, p4]:
if p in points:
points.remove(p)
else:
points.add(p)
# 判断面积是否相同
expectedArea = (X2 - X1) * (Y2 - Y1)
if actualArea != expectedArea:
return False
# 判断最终留下的顶点个数是否为 4
if len(points) != 4:
return False
# 判断留下的 4 个顶点是否是完美矩形的顶点
if not (f"{X1},{Y1}" in points and f"{X1},{Y2}" in points and f"{X2},{Y1}" in points and f"{X2},{Y2}" in points):
return False
# 面积和顶点都对应,说明矩形符合题意
return Truefunc isRectangleCover(rectangles [][]int) bool {
X1, Y1 := int(^uint(0)>>1), int(^uint(0)>>1)
X2, Y2 := -int(^uint(0)>>1)-1, -int(^uint(0)>>1)-1
points := make(map[string]bool)
actualArea := 0
for _, rect := range rectangles {
x1, y1, x2, y2 := rect[0], rect[1], rect[2], rect[3]
// 计算完美矩形的理论顶点坐标
if x1 < X1 { X1 = x1 }
if y1 < Y1 { Y1 = y1 }
if x2 > X2 { X2 = x2 }
if y2 > Y2 { Y2 = y2 }
// 累加小矩形的面积
actualArea += (x2 - x1) * (y2 - y1)
// 记录最终形成的图形中的顶点
p1 := fmt.Sprintf("%d,%d", x1, y1)
p2 := fmt.Sprintf("%d,%d", x1, y2)
p3 := fmt.Sprintf("%d,%d", x2, y1)
p4 := fmt.Sprintf("%d,%d", x2, y2)
for _, p := range []string{p1, p2, p3, p4} {
if points[p] {
delete(points, p)
} else {
points[p] = true
}
}
}
// 判断面积是否相同
expectedArea := (X2 - X1) * (Y2 - Y1)
if actualArea != expectedArea {
return false
}
// 判断最终留下的顶点个数是否为 4
if len(points) != 4 {
return false
}
// 判断留下的 4 个顶点是否是完美矩形的顶点
if !points[fmt.Sprintf("%d,%d", X1, Y1)] ||
!points[fmt.Sprintf("%d,%d", X1, Y2)] ||
!points[fmt.Sprintf("%d,%d", X2, Y1)] ||
!points[fmt.Sprintf("%d,%d", X2, Y2)] {
return false
}
// 面积和顶点都对应,说明矩形符合题意
return true
}var isRectangleCover = function(rectangles) {
let X1 = Number.MAX_VALUE, Y1 = Number.MAX_VALUE;
let X2 = Number.MIN_VALUE, Y2 = Number.MIN_VALUE;
let points = new Set();
let actualArea = 0;
for (let rect of rectangles) {
let x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
// 计算完美矩形的理论顶点坐标
X1 = Math.min(X1, x1);
Y1 = Math.min(Y1, y1);
X2 = Math.max(X2, x2);
Y2 = Math.max(Y2, y2);
// 累加小矩形的面积
actualArea += (x2 - x1) * (y2 - y1);
// 记录最终形成的图形中的顶点
let p1 = x1 + "," + y1;
let p2 = x1 + "," + y2;
let p3 = x2 + "," + y1;
let p4 = x2 + "," + y2;
for (let p of [p1, p2, p3, p4]) {
if (points.has(p)) points.delete(p);
else points.add(p);
}
}
// 判断面积是否相同
let expectedArea = (X2 - X1) * (Y2 - Y1);
if (actualArea !== expectedArea) {
return false;
}
// 判断最终留下的顶点个数是否为 4
if (points.size !== 4) {
return false;
}
// 判断留下的 4 个顶点是否是完美矩形的顶点
if (!points.has(X1 + "," + Y1)) return false;
if (!points.has(X1 + "," + Y2)) return false;
if (!points.has(X2 + "," + Y1)) return false;
if (!points.has(X2 + "," + Y2)) return false;
// 面积和顶点都对应,说明矩形符合题意
return true;
};算法可视化面板
这就是最终的解法代码,从「面积」和「顶点」两个维度来判断:
1、判断面积,通过完美矩形的理论坐标计算出一个理论面积,然后和 rectangles 中小矩形的实际面积和做对比。
2、判断顶点,points 集合中应该只剩下 4 个顶点且剩下的顶点必须都是完美矩形的理论顶点。