常用的位操作
本文讲解的例题
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 136. Single Number | 136. 只出现一次的数字 | 🟢 |
| 191. Number of 1 Bits | 191. 位1的个数 | 🟢 |
| 231. Power of Two | 231. 2 的幂 | 🟢 |
| 268. Missing Number | 268. 丢失的数字 | 🟢 |
位操作(Bit Manipulation)可以有很多技巧,有一个叫做 Bit Twiddling Hacks 的网站收集了几乎所有位操作的黑科技玩法,网址如下:
http://graphics.stanford.edu/~seander/bithacks.html
但是这些技巧大部分都过于晦涩,我觉得可以作为字典查阅,没必要逐条深究。但我认为那些有趣的、有用的位运算技巧,是我们每个人需要掌握的。
所以本文由浅入深,现介绍一些基本的位运算原理,再汇总一些在算法题以及工程开发中常用的位运算技巧。
位运算基础
二进制表示
在计算机中,所有的数据最终都是以二进制形式存储的。二进制只有 0 和 1 两个数字,每一位称为一个比特(bit)。
例如,十进制数字 13 的二进制表示是 1101,我们可以这样理解:
1101 = 1×2³ + 1×2² + 0×2¹ + 1×2⁰ = 8 + 4 + 0 + 1 = 13在 Java 等编程语言中,我们可以用 0b 前缀来表示二进制数字:
int a = 0b1101; // 等价于十进制的 13
int b = 0b1010; // 等价于十进制的 10位移运算
左移运算 <<:将二进制数向左移动若干位,右边用 0 补齐。左移 n 位相当于乘以 2^n。
int a = 5; // 二进制: 0b0101
int b = a << 1; // 二进制: 0b1010,十进制: 10
int c = a << 2; // 二进制: 0b10100,十进制: 20
// 左移 n 位相当于乘以 2^n
// 5 << 1 = 5 * 2¹ = 10
// 5 << 2 = 5 * 2² = 20右移运算 >>:将二进制数向右移动若干位,左边用符号位补齐。右移 n 位相当于除以 2^n(向下取整)。
int a = 20; // 二进制: 0b10100
int b = a >> 1; // 二进制: 0b1010,十进制: 10
int c = a >> 2; // 二进制: 0b101,十进制: 5
// 右移 n 位相当于除以 2^n
// 20 >> 1 = 20 / 2¹ = 10
// 20 >> 2 = 20 / 2² = 5与运算(AND)
与运算 &:两个对应的二进制位都为 1 时,结果才为 1,否则为 0。
int a = 12; // 二进制: 0b1100
int b = 10; // 二进制: 0b1010
int c = a & b; // 二进制: 0b1000,十进制: 8
// 逐位分析:
// 1100
// 1010
// ----
// 1000常见应用:
- 判断奇偶性:
n & 1,结果为 1 表示奇数,为 0 表示偶数 - 取出某一位:
n & (1 << k)可以取出 n 的第 k 位
int n = 13; // 二进制: 0b1101
boolean isOdd = (n & 1) == 1; // true,13 是奇数
// 取出第 2 位(从右往左,从 0 开始计数)
int bit2 = (n & (1 << 2)) != 0 ? 1 : 0; // 结果为 1或运算(OR)
或运算 |:两个对应的二进制位只要有一个为 1,结果就为 1。
int a = 12; // 二进制: 0b1100
int b = 10; // 二进制: 0b1010
int c = a | b; // 二进制: 0b1110,十进制: 14
// 逐位分析:
// 1100
// 1010
// ----
// 1110常见应用:
- 设置某一位为 1:
n | (1 << k)可以将 n 的第 k 位设置为 1
int n = 12; // 二进制: 0b1100
n = n | (1 << 0); // 将第 0 位设为 1,结果: 0b1101,十进制: 13异或运算(XOR)
异或运算 ^:两个对应的二进制位相同时为 0,不同时为 1。
int a = 12; // 二进制: 0b1100
int b = 10; // 二进制: 0b1010
int c = a ^ b; // 二进制: 0b0110,十进制: 6
// 逐位分析:
// 1100
// 1010
// ----
// 0110异或运算的重要性质:
a ^ a = 0:任何数和自己异或的结果是 0a ^ 0 = a:任何数和 0 异或的结果是它本身- 异或运算满足交换律和结合律:
a ^ b ^ c = a ^ (b ^ c) = (a ^ b) ^ c
int a = 5;
int result1 = a ^ a; // 结果为 0
int result2 = a ^ 0; // 结果为 5
// 交换律和结合律
int x = 3, y = 5, z = 7;
int r1 = x ^ y ^ z; // 结果为 1
int r2 = x ^ (y ^ z); // 结果为 1
int r3 = (x ^ y) ^ z; // 结果为 1常见应用:
- 翻转某一位:
n ^ (1 << k)可以翻转 n 的第 k 位(0 变 1,1 变 0) - 交换两个数(后面会详细介绍)
int n = 12; // 二进制: 0b1100
n = n ^ (1 << 0); // 翻转第 0 位,结果: 0b1101,十进制: 13
n = n ^ (1 << 0); // 再次翻转第 0 位,结果: 0b1100,十进制: 12理解了这些基础的位运算,我们就可以来看一些有趣的位操作技巧了。
几个有趣的位操作
// 1. 利用或操作 `|` 和空格将英文字符转换为小写
('a' | ' ') = 'a'
('A' | ' ') = 'a'
// 2. 利用与操作 `&` 和下划线将英文字符转换为大写
('b' & '_') = 'B'
('B' & '_') = 'B'
// 3. 利用异或操作 `^` 和空格进行英文字符大小写互换
('d' ^ ' ') = 'D'
('D' ^ ' ') = 'd'
// 以上操作能够产生奇特效果的原因在于 ASCII 编码
// ASCII 字符其实就是数字,恰巧空格和下划线对应的数字通过位运算就能改变大小写
// 有兴趣的读者可以查 ASCII 码表自己算算,我就不展开讲了
// 4. 不用临时变量交换两个数
int a = 1, b = 2;
a ^= b;
b ^= a;
a ^= b;
// 现在 a = 2, b = 1
// 5. 加一
int n = 1;
n = -~n;
// 现在 n = 2
// 6. 减一
int n = 2;
n = ~-n;
// 现在 n = 1
// 7. 判断两个数是否异号
int x = -1, y = 2;
boolean f = ((x ^ y) < 0); // true
int x = 3, y = 2;
boolean f = ((x ^ y) < 0); // false如果说前 6 个技巧的用处不大,这第 7 个技巧还是比较实用的,利用的是补码编码的符号位。整数编码最高位是符号位,负数的符号位是 1,非负数的符号位是 0,再借助异或的特性,可以判断出两个数字是否异号。
当然,如果不用位运算来判断是否异号,需要使用 if else 分支,还挺麻烦的。你可能想利用乘积来判断两个数是否异号,但是这种处理方式容易造成整型溢出,从而出现错误。
对 2 的幂取模
对于「求模(取余)运算」,我们常用 % 运算符。但你可能在一些代码实现(比如 HashMap 的源码)中看到过 & 运算的身影,这其实是一种优化手段。
当模数 m 是 2 的幂时,x % m 等价于 x & (m - 1)。
位运算 & 的效率比 % 高得多,所以这个技巧在性能敏感的场景中非常有用。
一个常见的应用场景就是实现环形数组。常规的实现方式是利用求模运算,让数组索引在 [0, arr.length - 1] 之间循环:
int[] arr = {1,2,3,4};
int index = 0;
while (true) {
// 在环形数组中转圈
print(arr[index % arr.length]);
index++;
}
// 输出:1,2,3,4,1,2,3,4,1,2,3,4...int arr[] = {1, 2, 3, 4};
int index = 0;
while (true) {
// 绕着循环数组走
cout << arr[index % (sizeof(arr) / sizeof(int))] << endl;
index++;
}
// 输出:1,2,3,4,1,2,3,4,1,2,3,4...arr = [1,2,3,4]
index = 0
while True:
# 在环形数组中转圈
print(arr[index % len(arr)])
index += 1
# 输出:1,2,3,4,1,2,3,4,1,2,3,4...arr := []int{1, 2, 3, 4}
index := 0
for {
// 在环形数组中转圈
fmt.Print(arr[index%len(arr)])
index++
}
// 输出:1,2,3,4,1,2,3,4,1,2,3,4...var arr = [1, 2, 3, 4];
var index = 0;
while (true) {
// 在环形数组中转圈
console.log(arr[index % arr.length]);
index++;
}
// 输出:1,2,3,4,1,2,3,4,1,2,3,4...如果数组的长度恰好是 2 的幂,我们就可以用 & 运算来优化求模操作:
int[] arr = {1,2,3,4};
int index = 0;
while (true) {
// 在环形数组中转圈
print(arr[index & (arr.length - 1)]);
index++;
}
// 输出:1,2,3,4,1,2,3,4,1,2,3,4...vector<int> arr = {1, 2, 3, 4};
int index = 0;
while (true) {
// 在环形数组中转圈
cout << arr[index & (arr.size() - 1)] << " ";
index++;
}
// 输出:1,2,3,4,1,2,3,4,1,2,3,4...arr = [1, 2, 3, 4]
index = 0
while True:
# 在环形数组中转圈
print(arr[index & (len(arr) - 1)], end=", ")
index += 1
# 输出:1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4, ...arr := []int{1, 2, 3, 4}
index := 0
for {
// 在环形数组中转圈
fmt.Print(arr[index&(len(arr)-1)])
index++
}
// 输出:1,2,3,4,1,2,3,4,1,2,3,4...var arr = [1,2,3,4];
var index = 0;
while (true) {
// 在环形数组中转圈
console.log(arr[index & (arr.length - 1)]);
index++;
}
// 输出:1,2,3,4,1,2,3,4,1,2,3,4...Important
注意这个技巧只适用于数组长度是 2 的幂次方的情况,比如 2、4、8、16、32 以此类推。至于如何将数组长度扩展为 2 的幂次方,这也是有比较巧妙的位运算算法的,可以参考 https://graphics.stanford.edu/~seander/bithacks.html#RoundUpPowerOf2
简单说,& (arr.length - 1) 这个位运算能够替代 % arr.length 的模运算,性能会更好一些。
那问题来了,现在是不断地 index++,你做到了循环遍历。但如果不断地 index--,还能做到环形数组的效果吗?
答案是,如果你使用 % 求模的方式,那么当 index 小于 0 之后求模的结果也会出现负数,你需要特殊处理。但通过 & 与运算的方式,index 不会出现负数,依然可以正常工作:
int[] arr = {1,2,3,4};
int index = 0;
while (true) {
// 在环形数组中转圈
print(arr[index & (arr.length - 1)]);
index--;
}
// 输出:1,4,3,2,1,4,3,2,1,4,3,2,1...int arr[] = {1,2,3,4};
int index = 0;
while (true) {
// 在环形数组中转圈
cout << arr[index & (sizeof(arr) / sizeof(*arr) - 1)] << " ";
index--;
}
// 输出:1,4,3,2,1,4,3,2,1,4,3,2,1...arr = [1, 2, 3, 4]
index = 0
while True:
# 在环形数组中转圈
print(arr[index & (len(arr) - 1)])
index -= 1arr := []int{1, 2, 3, 4}
index := 0
for {
// 在环形数组中转圈
fmt.Print(arr[index&(len(arr)-1)])
index--
}
// 输出:1,4,3,2,1,4,3,2,1,4,3,2,1...var arr = [1,2,3,4];
var index = 0;
while (true) {
console.log(arr[index & (arr.length - 1)]);
index--;
}
// 输出:1,4,3,2,1,4,3,2,1,4,3,2,1...我们自己写代码一般用不到这个技巧,但在学习一些其他代码库时可能会经常看到,这里留个印象,到时候就不会懵逼了。
n & (n-1) 的运用
n & (n-1) 这个操作在算法中比较常见,作用是消除数字 n 的二进制表示中的最后一个 1。
看个图就很容易理解了:
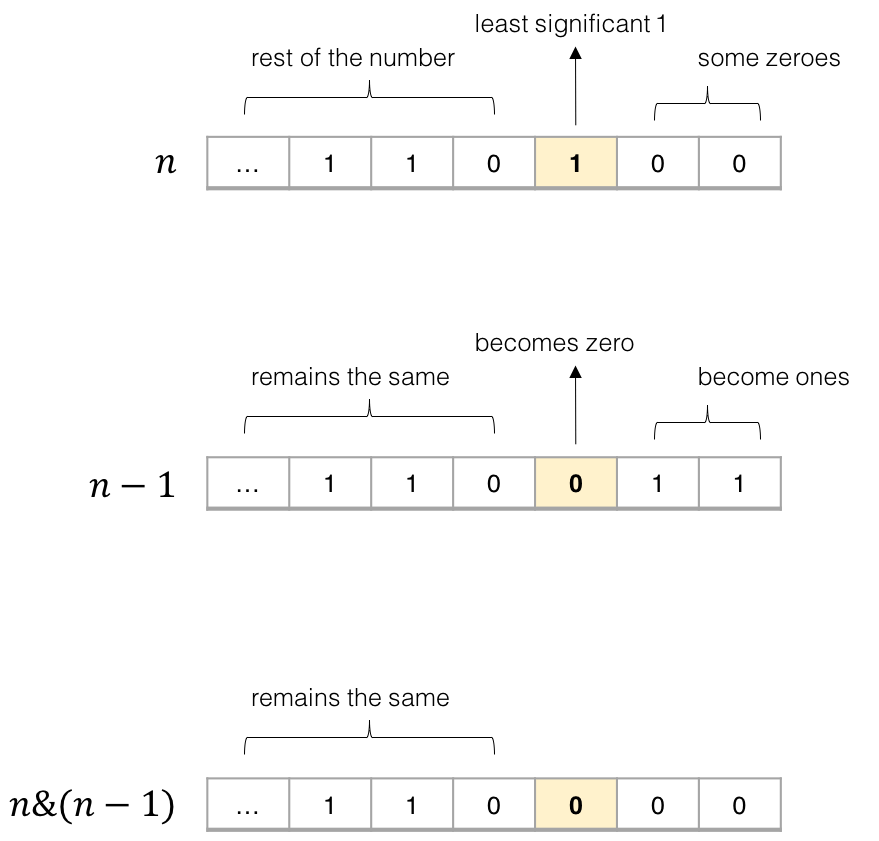
其核心逻辑就是,n - 1 一定可以消除最后一个 1,同时把其后的 0 都变成 1,这样再和 n 做一次 & 运算,就可以仅仅把最后一个 1 变成 0 了。
计算汉明权重(Hamming Weight)
这是力扣第 191 题「位 1 的个数」:
191. 位1的个数 | 力扣 | LeetCode | 🟢
编写一个函数,获取一个正整数的二进制形式并返回其二进制表达式中 设置位 的个数(也被称为汉明重量)。
示例 1:
输入:n = 11
输出:3
解释:输入的二进制串 1011 中,共有 3 个设置位。
示例 2:
输入:n = 128 输出:1 解释:输入的二进制串 10000000 中,共有 1 个设置位。
示例 3:
输入:n = 2147483645 输出:30 解释:输入的二进制串 11111111111111111111111111111101 中,共有 30 个设置位。
提示:
1 <= n <= 231 - 1
进阶:
- 如果多次调用这个函数,你将如何优化你的算法?
就是让你返回 n 的二进制表示中有几个 1。因为 n & (n - 1) 可以消除最后一个 1,所以可以用一个循环不停地消除 1 同时计数,直到 n 变成 0 为止。
public class Solution {
// you need to treat n as an unsigned value
public int hammingWeight(int n) {
int res = 0;
while (n != 0) {
n = n & (n - 1);
res++;
}
return res;
}
}#include <vector>
#include <string>
class Solution {
public:
int hammingWeight(uint32_t n) {
int res = 0;
while (n != 0) {
n = n & (n - 1);
res++;
}
return res;
}
};class Solution:
def hammingWeight(self, n: int) -> int:
res = 0
while n != 0:
n = n & (n - 1)
res += 1
return resfunc hammingWeight(n int) int {
res := 0
for n != 0 {
n = n & (n - 1)
res++
}
return res
}var hammingWeight = function(n) {
let res = 0;
while (n != 0) {
n = n & (n - 1);
res++;
}
return res;
};判断 2 的指数
力扣第 231 题「2 的幂」就是这个问题。
一个数如果是 2 的指数,那么它的二进制表示一定只含有一个 1:
2^0 = 1 = 0b0001
2^1 = 2 = 0b0010
2^2 = 4 = 0b0100如果使用 n & (n-1) 的技巧就很简单了(注意运算符优先级,括号不可以省略):
class Solution {
public boolean isPowerOfTwo(int n) {
if (n <= 0) return false;
return (n & (n - 1)) == 0;
}
}class Solution {
public:
bool isPowerOfTwo(int n) {
if (n <= 0) return false;
return (n & (n - 1)) == 0;
}
};class Solution:
def isPowerOfTwo(self, n: int) -> bool:
if n <= 0:
return False
return (n & (n - 1)) == 0func isPowerOfTwo(n int) bool {
if n <= 0 {
return false
}
return (n & (n - 1)) == 0
}var isPowerOfTwo = function(n) {
if (n <= 0) return false;
return (n & (n - 1)) === 0;
};a ^ a = 0 的运用
异或运算的性质是需要我们牢记的:
一个数和它本身做异或运算结果为 0,即 a ^ a = 0;一个数和 0 做异或运算的结果为它本身,即 a ^ 0 = a。
查找只出现一次的元素
这是力扣第 136 题「只出现一次的数字」:
136. 只出现一次的数字 | 力扣 | LeetCode | 🟢
给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
示例 1 :
输入:nums = [2,2,1] 输出:1
示例 2 :
输入:nums = [4,1,2,1,2] 输出:4
示例 3 :
输入:nums = [1] 输出:1
提示:
1 <= nums.length <= 3 * 104-3 * 104 <= nums[i] <= 3 * 104- 除了某个元素只出现一次以外,其余每个元素均出现两次。
对于这道题目,我们只要把所有数字进行异或,成对儿的数字就会变成 0,落单的数字和 0 做异或还是它本身,所以最后异或的结果就是只出现一次的元素:
class Solution {
public int singleNumber(int[] nums) {
int res = 0;
for (int n : nums) {
res ^= n;
}
return res;
}
}#include <vector>
class Solution {
public:
int singleNumber(std::vector<int>& nums) {
int res = 0;
for (int n : nums) {
res ^= n;
}
return res;
}
};class Solution:
def singleNumber(self, nums: List[int]) -> int:
res = 0
for n in nums:
res ^= n
return resfunc singleNumber(nums []int) int {
res := 0
for _, n := range nums {
res ^= n
}
return res
}var singleNumber = function(nums) {
let res = 0;
for (let n of nums) {
res ^= n;
}
return res;
};寻找缺失的元素
这是力扣第 268 题「丢失的数字」:
268. 丢失的数字 | 力扣 | LeetCode | 🟢
给定一个包含 [0, n] 中 n 个数的数组 nums ,找出 [0, n] 这个范围内没有出现在数组中的那个数。
示例 1:
输入:nums = [3,0,1] 输出:2 解释:n = 3,因为有 3 个数字,所以所有的数字都在范围 [0,3] 内。2 是丢失的数字,因为它没有出现在 nums 中。
示例 2:
输入:nums = [0,1] 输出:2 解释:n = 2,因为有 2 个数字,所以所有的数字都在范围 [0,2] 内。2 是丢失的数字,因为它没有出现在 nums 中。
示例 3:
输入:nums = [9,6,4,2,3,5,7,0,1] 输出:8 解释:n = 9,因为有 9 个数字,所以所有的数字都在范围 [0,9] 内。8 是丢失的数字,因为它没有出现在 nums 中。
示例 4:
输入:nums = [0] 输出:1 解释:n = 1,因为有 1 个数字,所以所有的数字都在范围 [0,1] 内。1 是丢失的数字,因为它没有出现在 nums 中。
提示:
n == nums.length1 <= n <= 1040 <= nums[i] <= nnums中的所有数字都 独一无二
进阶:你能否实现线性时间复杂度、仅使用额外常数空间的算法解决此问题?
给一个长度为 n 的数组,其索引应该在 [0,n),但是现在你要装进去 n + 1 个元素 [0,n],那么肯定有一个元素装不下嘛,请你找出这个缺失的元素。
这道题不难的,我们应该很容易想到,把这个数组排个序,然后遍历一遍,不就很容易找到缺失的那个元素了吗?
或者说,借助数据结构的特性,用一个 HashSet 把数组里出现的数字都储存下来,再遍历 [0,n] 之间的数字,去 HashSet 中查询,也可以很容易查出那个缺失的元素。
排序解法的时间复杂度是 O(NlogN),HashSet 的解法时间复杂度是 O(N),但是还需要 O(N) 的空间复杂度存储 HashSet。
这个问题其实还有一个特别简单的解法:等差数列求和公式。
题目的意思可以这样理解:现在有个等差数列 0, 1, 2,..., n,其中少了某一个数字,请你把它找出来。那这个数字不就是 sum(0,1,..n) - sum(nums) 嘛?
int missingNumber(int[] nums) {
int n = nums.length;
// 虽然题目给的数据范围不大,但严谨起见,用 long 类型防止整型溢出
// 求和公式:(首项 + 末项) * 项数 / 2
long expect = (0 + n) * (n + 1) / 2;
long sum = 0;
for (int x : nums) {
sum += x;
}
return (int)(expect - sum);
}int missingNumber(vector<int>& nums) {
int n = nums.size();
// 虽然题目给的数据范围不大,但严谨起见,用 long 类型防止整型溢出
// 求和公式:(首项 + 末项) * 项数 / 2
long expect = (0 + n) * (n + 1) / 2;
long sum = 0;
for (int x : nums) {
sum += x;
}
return (int)(expect - sum);
}from typing import List
def missingNumber(nums: List[int]) -> int:
n = len(nums)
# 虽然题目给的数据范围不大,但严谨起见,用 long 类型防止整型溢出
# 求和公式:(首项 + 末项) * 项数 / 2
expect = (0 + n) * (n + 1) / 2
sum_ = 0
for x in nums:
sum_ += x
return int(expect - sum_)func missingNumber(nums []int) int {
n := len(nums)
// 虽然题目给的数据范围不大,但严谨起见,用 long 类型防止整型溢出
// 求和公式:(首项 + 末项) * 项数 / 2
expect := (0 + n) * (n + 1) / 2
var sum int64
for _, x := range nums {
sum += int64(x)
}
return int(expect - sum)
}var missingNumber = function(nums) {
var n = nums.length;
// 虽然题目给的数据范围不大,但严谨起见,用 long 类型防止整型溢出
// 求和公式:(首项 + 末项) * 项数 / 2
var expect = (0 + n) * (n + 1) / 2;
var sum = 0;
for (var i = 0; i < n; i++) {
sum += nums[i];
}
return (expect - sum);
};不过,本文的主题是位运算,我们来讲讲如何利用位运算技巧来解决这道题。
再回顾一下异或运算的性质:一个数和它本身做异或运算结果为 0,一个数和 0 做异或运算还是它本身。
而且异或运算满足交换律和结合律,也就是说:
2 ^ 3 ^ 2 = 3 ^ (2 ^ 2) = 3 ^ 0 = 3而这道题索就可以通过这些性质巧妙算出缺失的那个元素,比如说 nums = [0,3,1,4]:
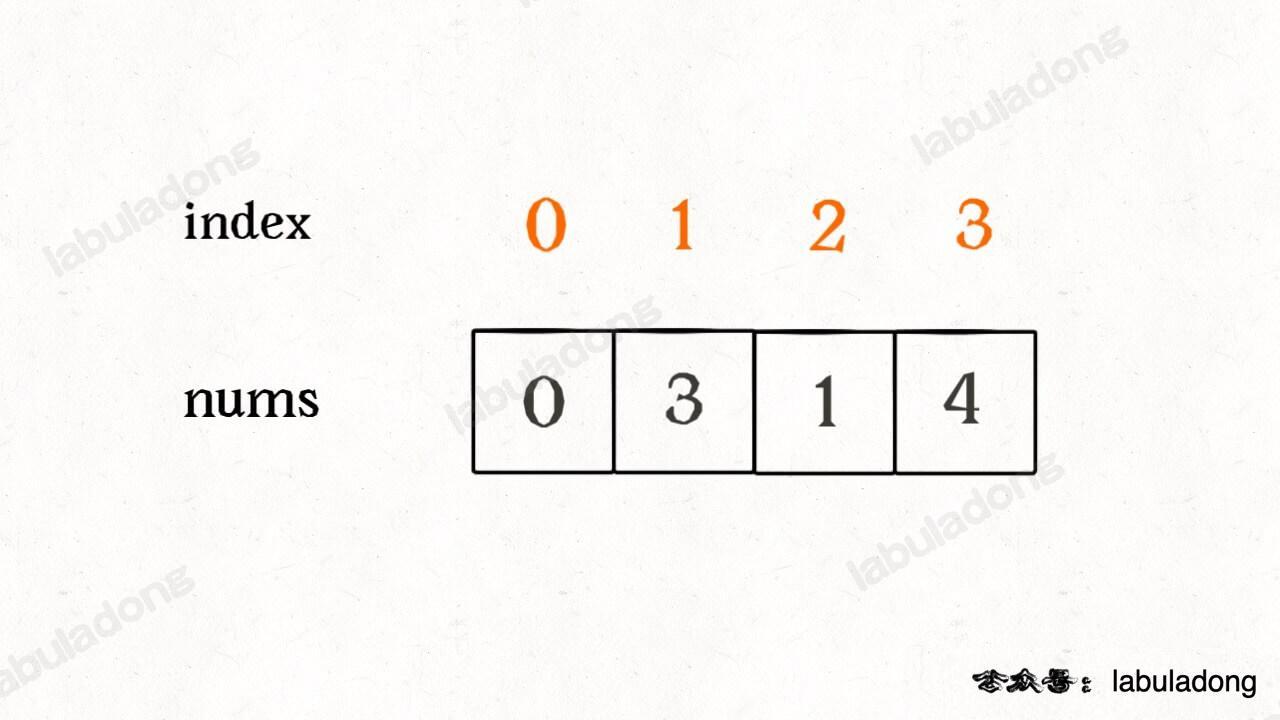
为了容易理解,我们假设先把索引补一位,然后让每个元素和自己相等的索引相对应:
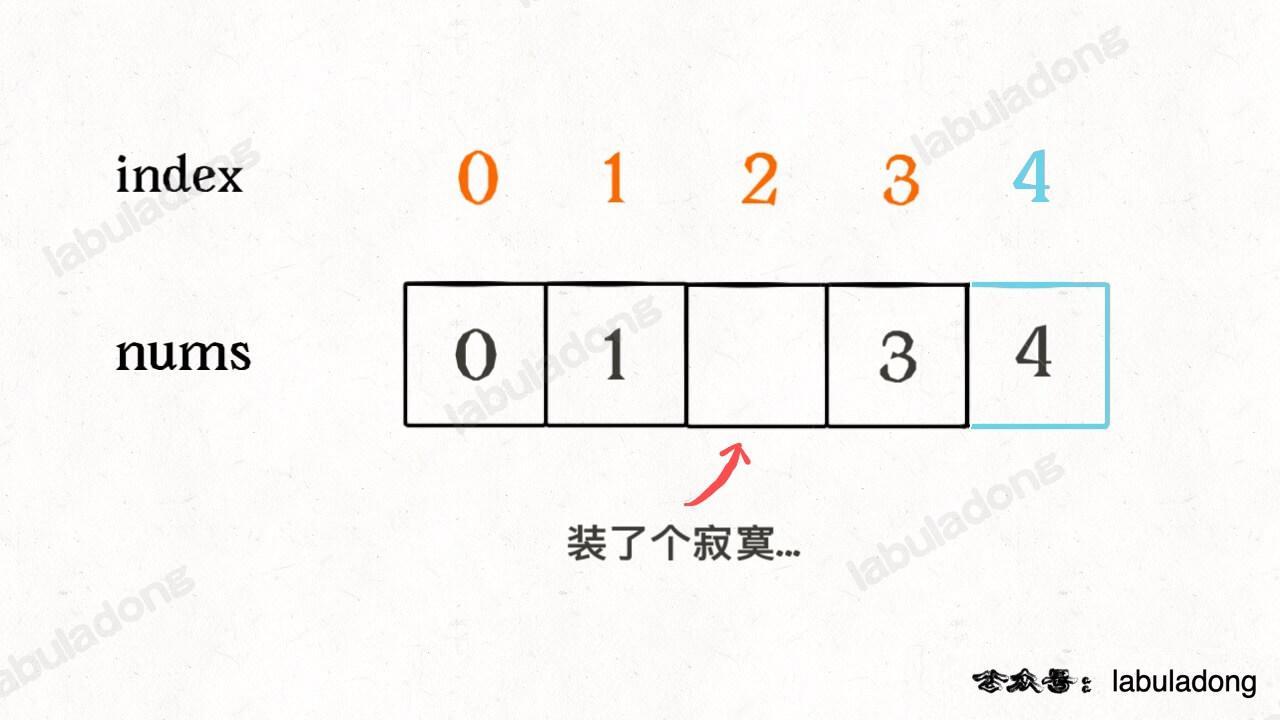
这样做了之后,就可以发现除了缺失元素之外,所有的索引和元素都组成一对儿了,现在如果把这个落单的索引 2 找出来,也就找到了缺失的那个元素。
如何找这个落单的数字呢,只要把所有的元素和索引做异或运算,成对儿的数字都会消为 0,只有这个落单的元素会剩下,也就达到了我们的目的:
class Solution {
public int missingNumber(int[] nums) {
int n = nums.length;
int res = 0;
// 先和新补的索引异或一下
res ^= n;
// 和其他的元素、索引做异或
for (int i = 0; i < n; i++)
res ^= i ^ nums[i];
return res;
}
}#include <vector>
using namespace std;
class Solution {
public:
int missingNumber(vector<int>& nums) {
int n = nums.size();
int res = 0;
// 先和新补的索引异或一下
res ^= n;
// 和其他的元素、索引做异或
for (int i = 0; i < n; i++)
res ^= i ^ nums[i];
return res;
}
};class Solution:
def missingNumber(self, nums: List[int]) -> int:
n = len(nums)
res = 0
# 先和新补的索引异或一下
res ^= n
# 和其他的元素、索引做异或
for i in range(n):
res ^= i ^ nums[i]
return resfunc missingNumber(nums []int) int {
n := len(nums)
res := 0
// 先和新补的索引异或一下
res ^= n
// 和其他的元素、索引做异或
for i := 0; i < n; i++ {
res ^= i ^ nums[i]
}
return res
}var missingNumber = function(nums) {
let n = nums.length;
let res = 0;
// 先和新补的索引异或一下
res ^= n;
// 和其他的元素、索引做异或
for (let i = 0; i < n; i++)
res ^= i ^ nums[i];
return res;
};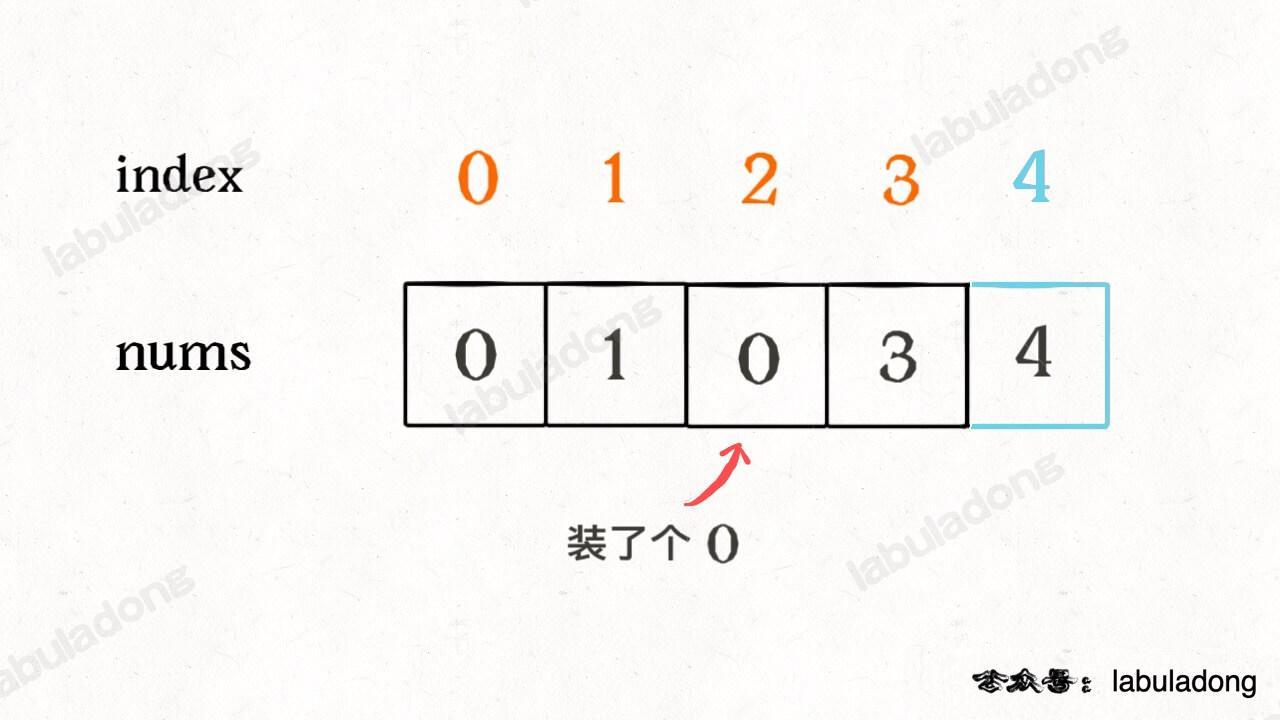
由于异或运算满足交换律和结合律,所以总是能把成对儿的数字消去,留下缺失的那个元素。
到这里,常见的位运算差不多都讲完了。这些技巧就是会者不难难者不会,也不需要死记硬背,只要有个印象就完全够用了。