实际运用二分搜索时的思维框架
原创约 5252 字
本文讲解的例题
| LeetCode | 力扣 | 难度 |
|---|---|---|
| 410. Split Array Largest Sum | 410. 分割数组的最大值 | 🔴 |
| 875. Koko Eating Bananas | 875. 爱吃香蕉的珂珂 | 🟠 |
| 1011. Capacity To Ship Packages Within D Days | 1011. 在 D 天内送达包裹的能力 | 🟠 |
在 二分查找框架详解 中我们详细研究了二分搜索的细节问题，探讨了「搜索一个元素」，「搜索左侧边界」，「搜索右侧边界」这三个情况，教你如何写出正确无 bug 的二分搜索算法。
但是前文总结的二分搜索代码框架仅仅局限于「在有序数组中搜索指定元素」这个基本场景，具体的算法问题没有这么直接，可能你都很难看出这个问题能够用到二分搜索。
所以本文就来总结一套二分搜索算法运用的框架套路，帮你在遇到二分搜索算法相关的实际问题时，能够有条理地思考分析，步步为营，写出答案。
原始的二分搜索代码
二分搜索的原型就是在「有序数组」中搜索一个元素 target，返回该元素对应的索引。
如果该元素不存在，那可以返回一个什么特殊值，这种细节问题只要微调算法实现就可实现。
还有一个重要的问题，如果「有序数组」中存在多个 target 元素，那么这些元素肯定挨在一起，这里就涉及到算法应该返回最左侧的那个 target 元素的索引还是最右侧的那个 target 元素的索引，也就是所谓的「搜索左侧边界」和「搜索右侧边界」，这个也可以通过微调算法的代码来实现。
我们前文 二分搜索核心框架 详细探讨了上述问题，对这块还不清楚的读者建议复习前文，已经搞清楚基本二分搜索算法的读者可以继续看下去。
在具体的算法问题中，常用到的是「搜索左侧边界」和「搜索右侧边界」这两种场景，很少有让你单独「搜索一个元素」。
因为算法题一般都让你求最值，比如让你求吃香蕉的「最小速度」，让你求轮船的「最低运载能力」，求最值的过程，必然是搜索一个边界的过程，所以后面我们就详细分析一下这两种搜索边界的二分算法代码。
注
注意，本文我写的都是左闭右开的二分搜索写法，如果你习惯两端都闭的写法，可以自行改写代码。
「搜索左侧边界」的二分搜索算法的具体代码实现如下：
java 🟢
// 搜索左侧边界
int left_bound(int[] nums, int target) {
if (nums.length == 0) return -1;
int left = 0, right = nums.length;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
// 当找到 target 时，收缩右侧边界
right = mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
return left;
}cpp 🤖
// 搜索左侧边界
int left_bound(vector<int>& nums, int target) {
if (nums.size() == 0) return -1;
int left = 0, right = nums.size();
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
// 当找到 target 时，收缩右侧边界
right = mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
return left;
}python 🤖
def left_bound(nums: List[int], target: int) -> int:
# 搜索左侧边界
if len(nums) == 0:
return -1
left, right = 0, len(nums)
while left < right:
mid = left + (right - left) // 2
if nums[mid] == target:
# 当找到 target 时，收缩右侧边界
right = mid
elif nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
right = mid
return leftgo 🤖
// 搜索左侧边界
func left_bound(nums []int, target int) int {
if len(nums) == 0 {
return -1
}
left, right := 0, len(nums)
for left < right {
mid := left + (right - left) / 2
if nums[mid] == target {
// 当找到 target 时，收缩右侧边界
right = mid
} else if nums[mid] < target {
left = mid + 1
} else if nums[mid] > target {
right = mid
}
}
return left
}javascript 🤖
// 搜索左侧边界
var left_bound = function(nums, target) {
if (nums.length === 0) return -1;
let left = 0, right = nums.length;
while (left < right) {
let mid = left + Math.floor((right - left) / 2);
if (nums[mid] === target) {
// 当找到 target 时，收缩右侧边界
right = mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
return left;
};假设输入的数组 nums = [1,2,3,3,3,5,7]，想搜索的元素 target = 3，那么算法就会返回索引 2。
如果画一个图，就是这样：
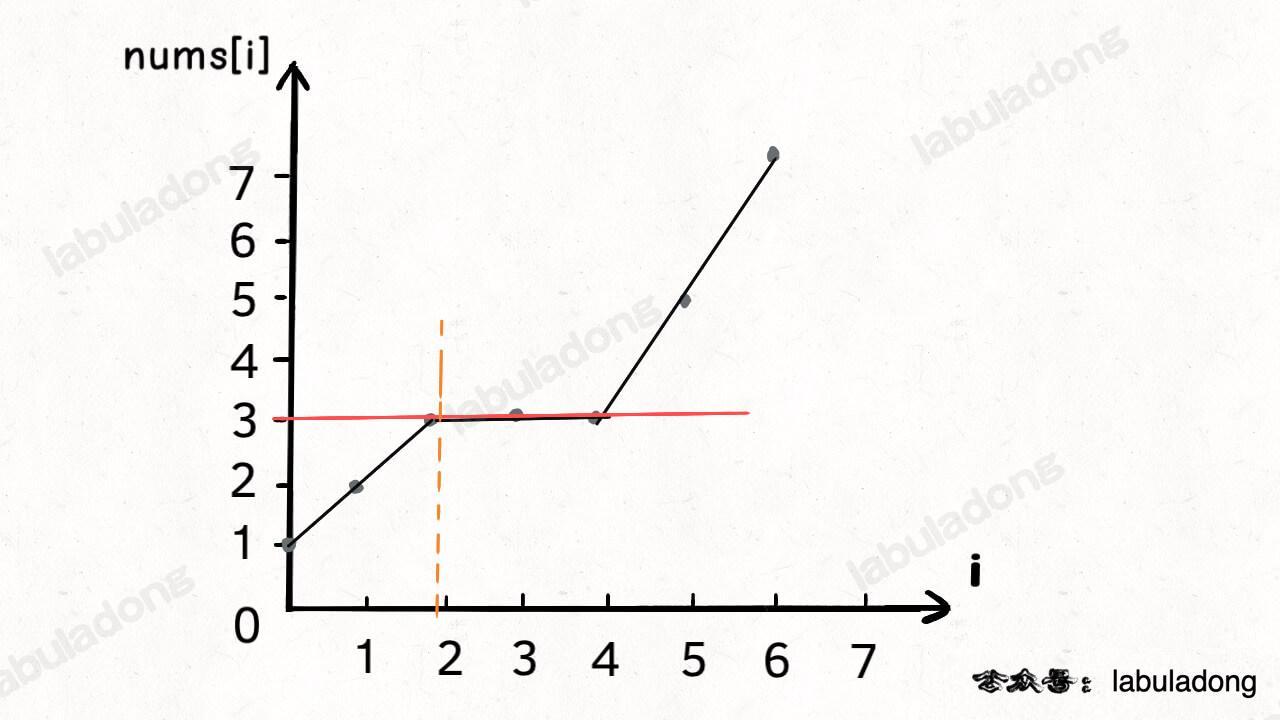
「搜索右侧边界」的二分搜索算法的具体代码实现如下：
java 🟢
// 搜索右侧边界
int right_bound(int[] nums, int target) {
if (nums.length == 0) return -1;
int left = 0, right = nums.length;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
// 当找到 target 时，收缩左侧边界
left = mid + 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
return left - 1;
}cpp 🤖
// 搜索右侧边界
int right_bound(vector<int>& nums, int target) {
if (nums.size() == 0) return -1;
int left = 0, right = nums.size();
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
// 当找到 target 时，收缩左侧边界
left = mid + 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
return left - 1;
}python 🤖
# 搜索右侧边界
def right_bound(nums: list[int], target: int) -> int:
if len(nums) == 0:
return -1
left, right = 0, len(nums)
while left < right:
mid = left + (right - left) // 2
if nums[mid] == target:
# 当找到 target 时，收缩左侧边界
left = mid + 1
elif nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
right = mid
return left - 1go 🤖
// 搜索右侧边界
func right_bound(nums []int, target int) int {
if len(nums) == 0 {
return -1
}
left, right := 0, len(nums)
for left < right {
mid := left + (right-left)/2
if nums[mid] == target {
// 当找到 target 时，收缩左侧边界
left = mid + 1
} else if nums[mid] < target {
left = mid + 1
} else if nums[mid] > target {
right = mid
}
}
return left - 1
}javascript 🤖
// 搜索右侧边界
var right_bound = function(nums, target) {
if (nums.length === 0) return -1;
let left = 0, right = nums.length;
while (left < right) {
let mid = left + Math.floor((right - left) / 2);
if (nums[mid] === target) {
// 当找到 target 时，收缩左侧边界
left = mid + 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
return left - 1;
};输入同上，那么算法就会返回索引 4，如果画一个图，就是这样：
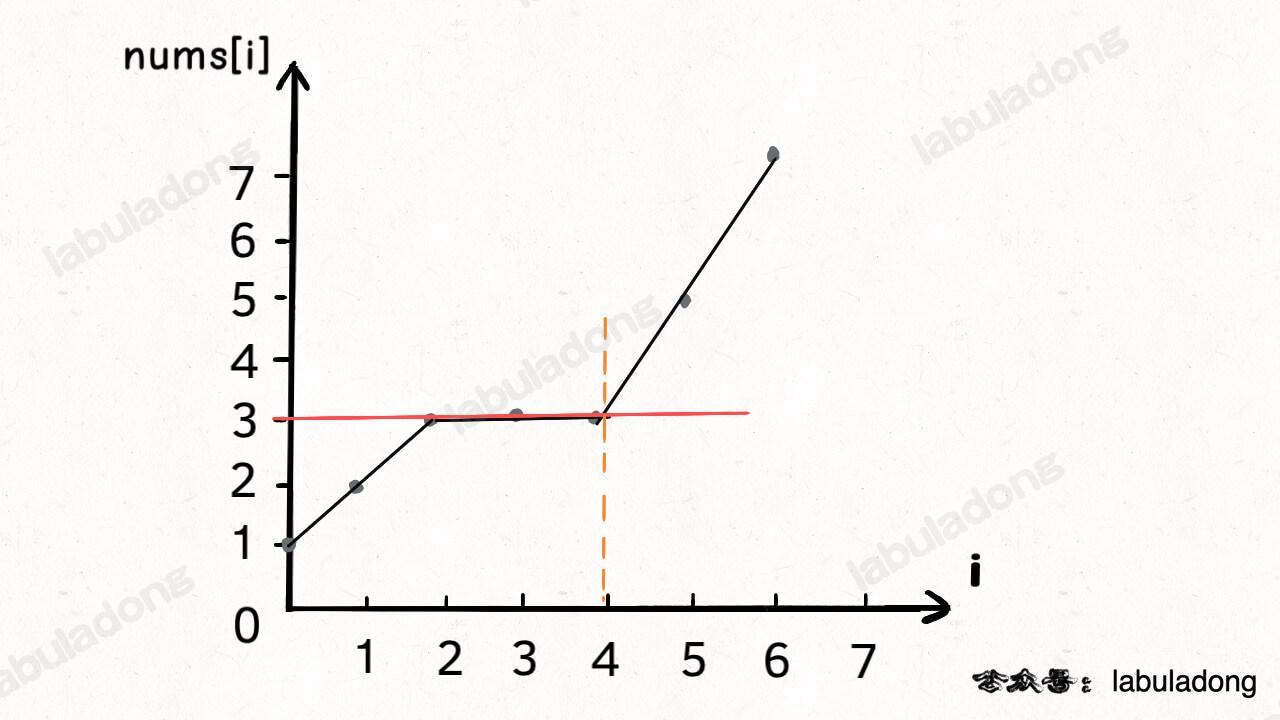
好，上述内容都属于复习，我想读到这里的读者应该都能理解。记住上述的图像，所有能够抽象出上述图像的问题，都可以使用二分搜索解决。