滑动窗口算法核心代码模板
本文讲解的例题
视频讲解

前文 双指针技巧汇总 讲解了一些较为简单的数组双指针技巧,本文就讲解一个稍微复杂的技巧:滑动窗口技巧。
滑动窗口可以归为快慢双指针,一快一慢两个指针前后相随,中间的部分就是窗口。滑动窗口算法技巧主要用来解决子数组问题,比如让你寻找符合某个条件的最长/最短子数组。
你可以点开下面的可视化面板,多次点击 while (right < s.length) 这一行代码,即可直观地看到窗口滑动的过程:
算法可视化面板
本文会总结出一套框架,可以保你闭着眼睛都能写出正确的解法,同时每道题目都配备了算法可视化面板,帮助你直观地理解窗口滑动的过程。
滑动窗口框架概览
如果用暴力解的话,你需要嵌套 for 循环这样穷举所有子数组,时间复杂度是 :
for (int i = 0; i < nums.length; i++) {
for (int j = i; j < nums.length; j++) {
// nums[i, j] 是一个子数组
}
}滑动窗口算法技巧的思路也不难,就是维护一个窗口,不断滑动,然后更新答案,该算法的大致逻辑如下:
// 索引区间 [left, right) 是窗口
int left = 0, right = 0;
while (right < nums.size()) {
// 增大窗口
window.addLast(nums[right]);
right++;
while (window needs shrink) {
// 缩小窗口
window.removeFirst(nums[left]);
left++;
}
}基于滑动窗口算法框架写出的代码,时间复杂度是 ,比嵌套 for 循环的暴力解法效率高。
为啥是 ?
肯定有读者要问了,你这个滑动窗口框架不也用了一个嵌套 while 循环?为啥复杂度是 呢?
简单说,指针 left, right 不会回退(它们的值只增不减),所以字符串/数组中的每个元素都只会进入窗口一次,然后被移出窗口一次,不会说有某些元素多次进入和离开窗口,所以算法的时间复杂度就和字符串/数组的长度成正比。
反观嵌套 for 循环的暴力解法,那个 j 会回退,所以某些元素会进入和离开窗口多次,所以时间复杂度就是 了。
我在 算法时空复杂度分析实用指南 有具体教大家如何从理论上估算时间空间复杂度,这里就不展开了。
为啥滑动窗口能在 的时间穷举子数组?
这个问题本身就是错误的,滑动窗口并不能穷举出所有子串。要想穷举出所有子串,必须用那个嵌套 for 循环。
然而对于某些题目,并不需要穷举所有子串,就能找到题目想要的答案。滑动窗口就是这种场景下的一套算法模板,帮你对穷举过程进行剪枝优化,避免冗余计算。
所以在 算法的本质 中我把滑动窗口算法归为「如何聪明地穷举」一类。
其实困扰大家的,不是算法的思路,而是各种细节问题。比如说如何向窗口中添加新元素,如何缩小窗口,在窗口滑动的哪个阶段更新结果。即便你明白了这些细节,代码也容易出 bug,找 bug 还不知道怎么找,真的挺让人心烦的。
所以今天我就写一套滑动窗口算法的代码框架,我连再哪里做输出 debug 都给你写好了,以后遇到相关的问题,你就默写出来如下框架然后改三个地方就行,保证不会出 bug。
因为本文的例题大多是子串相关的题目,字符串实际上就是数组,所以我就把输入设置成字符串了。你做题的时候根据具体题目自行变通即可:
// 滑动窗口算法伪码框架
void slidingWindow(String s) {
// 用合适的数据结构记录窗口中的数据,根据具体场景变通
// 比如说,我想记录窗口中元素出现的次数,就用 map
// 如果我想记录窗口中的元素和,就可以只用一个 int
Object window = ...
int left = 0, right = 0;
while (right < s.length()) {
// c 是将移入窗口的字符
char c = s[right];
window.add(c)
// 增大窗口
right++;
// 进行窗口内数据的一系列更新
...
// *** debug 输出的位置 ***
// 注意在最终的解法代码中不要 print
// 因为 IO 操作很耗时,可能导致超时
printf("window: [%d, %d)\n", left, right);
// ***********************
// 判断左侧窗口是否要收缩
while (left < right && window needs shrink) {
// d 是将移出窗口的字符
char d = s[left];
window.remove(d)
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
...
}
}
}// 滑动窗口算法伪码框架
void slidingWindow(string s) {
// 用合适的数据结构记录窗口中的数据,根据具体场景变通
// 比如说,我想记录窗口中元素出现的次数,就用 map
// 如果我想记录窗口中的元素和,就可以只用一个 int
auto window = ...
int left = 0, right = 0;
while (right < s.size()) {
// c 是将移入窗口的字符
char c = s[right];
window.add(c);
// 增大窗口
right++;
// 进行窗口内数据的一系列更新
...
// *** debug 输出的位置 ***
printf("window: [%d, %d)\n", left, right);
// 注意在最终的解法代码中不要 print
// 因为 IO 操作很耗时,可能导致超时
// 判断左侧窗口是否要收缩
while (window needs shrink) {
// d 是将移出窗口的字符
char d = s[left];
window.remove(d);
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
...
}
}
}# 滑动窗口算法伪码框架
def slidingWindow(s: str):
# 用合适的数据结构记录窗口中的数据,根据具体场景变通
# 比如说,我想记录窗口中元素出现的次数,就用 map
# 如果我想记录窗口中的元素和,就可以只用一个 int
window = ...
left, right = 0, 0
while right < len(s):
# c 是将移入窗口的字符
c = s[right]
window.add(c)
# 增大窗口
right += 1
# 进行窗口内数据的一系列更新
...
# *** debug 输出的位置 ***
# 注意在最终的解法代码中不要 print
# 因为 IO 操作很耗时,可能导致超时
# print(f"window: [{left}, {right})")
# ***********************
# 判断左侧窗口是否要收缩
while left < right and window needs shrink:
# d 是将移出窗口的字符
d = s[left]
window.remove(d)
# 缩小窗口
left += 1
# 进行窗口内数据的一系列更新
...// 滑动窗口算法伪码框架
func slidingWindow(s string) {
// 用合适的数据结构记录窗口中的数据,根据具体场景变通
// 比如说,我想记录窗口中元素出现的次数,就用 map
// 如果我想记录窗口中的元素和,就可以只用一个 int
var window = ...
left, right := 0, 0
for right < len(s) {
// c 是将移入窗口的字符
c := rune(s[right])
window[c]++
// 增大窗口
right++
// 进行窗口内数据的一系列更新
...
// *** debug 输出的位置 ***
// 注意在最终的解法代码中不要 print
// 因为 IO 操作很耗时,可能导致超时
fmt.Println("window: [",left,", ",right,")")
// ***********************
// 判断左侧窗口是否要收缩
for left < right && window needs shrink {
// d 是将移出窗口的字符
d := rune(s[left])
window[d]--
// 缩小窗口
left++
// 进行窗口内数据的一系列更新
...
}
}
}// 滑动窗口算法伪码框架
var slidingWindow = function(s) {
// 用合适的数据结构记录窗口中的数据,根据具体场景变通
// 比如说,我想记录窗口中元素出现的次数,就用 map
// 如果我想记录窗口中的元素和,就可以只用一个 int
var window = ...;
var left = 0, right = 0;
while (right < s.length) {
// c 是将移入窗口的字符
var c = s[right];
window.add(c);
// 增大窗口
right++;
// 进行窗口内数据的一系列更新
...
// *** debug 输出的位置 ***
// 注意在最终的解法代码中不要 print
// 因为 IO 操作很耗时,可能导致超时
console.log("window: [%d, %d)\n", left, right);
// *********************
// 判断左侧窗口是否要收缩
while (window needs shrink) {
// d 是将移出窗口的字符
var d = s[left];
window.remove(d);
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
...
}
}
};框架中两处 ... 表示的更新窗口数据的地方,在具体的题目中,你需要做的就是往这里面填代码逻辑。而且,这两个 ... 处的操作分别是扩大和缩小窗口的更新操作,等会你会发现它们操作是完全对称的。
基于这个框架,遇到子串/子数组相关的题目,你只需要回答以下三个问题:
1、什么时候应该移动 right 扩大窗口?窗口加入字符时,应该更新哪些数据?
2、什么时候窗口应该暂停扩大,开始移动 left 缩小窗口?从窗口移出字符时,应该更新哪些数据?
3、什么时候应该更新结果?
只要能回答这三个问题,就说明可以使用滑动窗口技巧解题。
下面就直接上四道力扣原题来套这个框架,其中第一道题会详细说明其原理,其他题目就直接闭眼睛秒杀了。
一、最小覆盖子串
先来看看力扣第 76 题「最小覆盖子串」难度 Hard:
76. 最小覆盖子串 | 力扣 | LeetCode | 🔴
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
注意:
- 对于
t中重复字符,我们寻找的子字符串中该字符数量必须不少于t中该字符数量。 - 如果
s中存在这样的子串,我们保证它是唯一的答案。
示例 1:
输入:s = "ADOBECODEBANC", t = "ABC" 输出:"BANC" 解释:最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。
示例 2:
输入:s = "a", t = "a" 输出:"a" 解释:整个字符串 s 是最小覆盖子串。
示例 3:
输入: s = "a", t = "aa" 输出: "" 解释: t 中两个字符 'a' 均应包含在 s 的子串中, 因此没有符合条件的子字符串,返回空字符串。
提示:
m == s.lengthn == t.length1 <= m, n <= 105s和t由英文字母组成
o(m+n) 时间内解决此问题的算法吗?就是说要在 S(source) 中找到包含 T(target) 中全部字母的一个子串,且这个子串一定是所有可能子串中最短的。
如果我们使用暴力解法,代码大概是这样的:
for (int i = 0; i < s.length(); i++)
for (int j = i + 1; j < s.length(); j++)
if s[i:j] 包含 t 的所有字母:
更新答案思路很直接,但是显然,这个算法的复杂度肯定大于 了,不好。
滑动窗口算法的思路是这样:
1、我们在字符串 S 中使用双指针中的左右指针技巧,初始化 left = right = 0,把索引左闭右开区间 [left, right) 称为一个「窗口」。
为什么要「左闭右开」区间
理论上你可以设计两端都开或者两端都闭的区间,但设计为左闭右开区间是最方便处理的。
因为这样初始化 left = right = 0 时区间 [0, 0) 中没有元素,但只要让 right 向右移动(扩大)一位,区间 [0, 1) 就包含一个元素 0 了。
如果你设置为两端都开的区间,那么让 right 向右移动一位后开区间 (0, 1) 仍然没有元素;如果你设置为两端都闭的区间,那么初始区间 [0, 0] 就包含了一个元素。这两种情况都会给边界处理带来不必要的麻烦。
2、我们先不断地增加 right 指针扩大窗口 [left, right),直到窗口中的字符串符合要求(包含了 T 中的所有字符)。
3、此时,我们停止增加 right,转而不断增加 left 指针缩小窗口 [left, right),直到窗口中的字符串不再符合要求(不包含 T 中的所有字符了)。同时,每次增加 left,我们都要更新一轮结果。
4、重复第 2 和第 3 步,直到 right 到达字符串 S 的尽头。
这个思路其实也不难,第 2 步相当于在寻找一个「可行解」,然后第 3 步在优化这个「可行解」,最终找到最优解,也就是最短的覆盖子串。左右指针轮流前进,窗口大小增增减减,就好像一条毛毛虫,一伸一缩,不断向右滑动,这就是「滑动窗口」这个名字的来历。
下面画图理解一下,needs 和 window 相当于计数器,分别记录 T 中字符出现次数和「窗口」中的相应字符的出现次数。
初始状态:
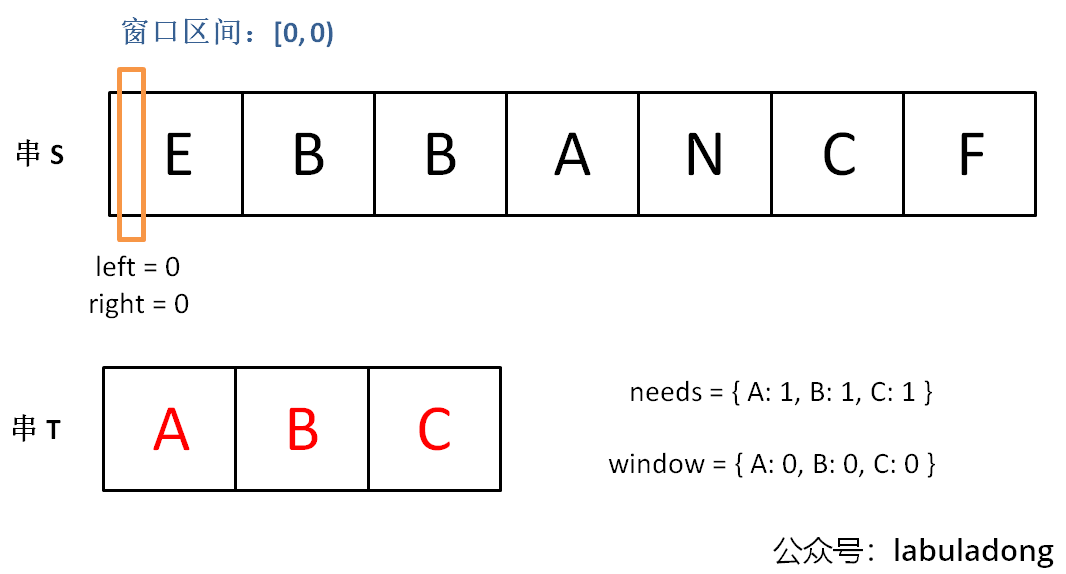
增加 right,直到窗口 [left, right) 包含了 T 中所有字符:
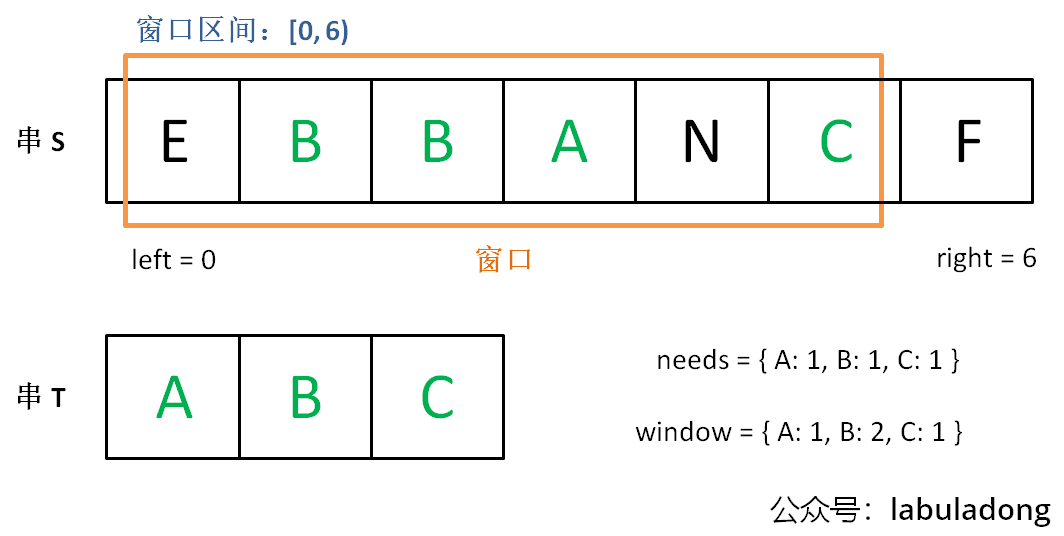
现在开始增加 left,缩小窗口 [left, right):
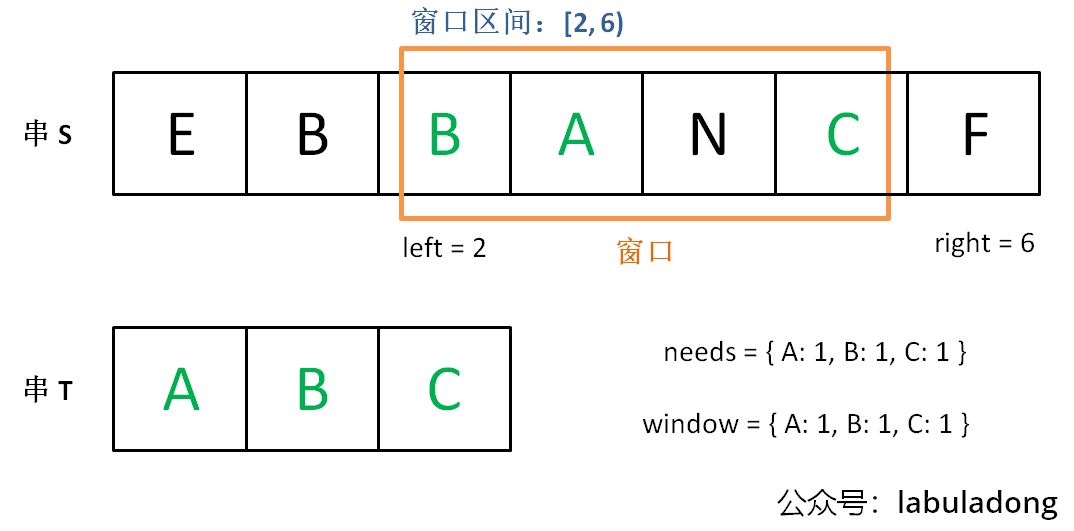
直到窗口中的字符串不再符合要求,left 不再继续移动:
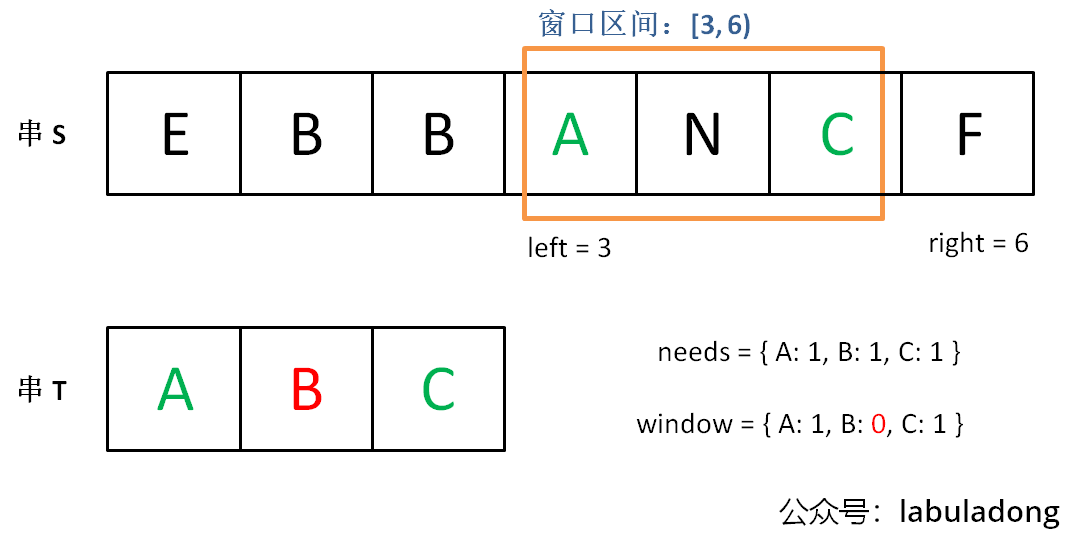
之后重复上述过程,先移动 right,再移动 left... 直到 right 指针到达字符串 S 的末端,算法结束。
如果你能够理解上述过程,恭喜,你已经完全掌握了滑动窗口算法思想。现在我们来看看这个滑动窗口代码框架怎么用:
首先,初始化 window 和 need 两个哈希表,记录窗口中的字符和需要凑齐的字符:
// 记录 window 中的字符出现次数
HashMap<Character, Integer> window = new HashMap<>();
// 记录所需的字符出现次数
HashMap<Character, Integer> need = new HashMap<>();
for (int i = 0; i < t.length(); i++) {
char c = t.charAt(i);
need.put(c, need.getOrDefault(c, 0) + 1);
}然后,使用 left 和 right 变量初始化窗口的两端,不要忘了,区间 [left, right) 是左闭右开的,所以初始情况下窗口没有包含任何元素:
int left = 0, right = 0;
int valid = 0;
while (right < s.length()) {
// c 是将移入窗口的字符
char c = s.charAt(right);
// 右移窗口
right++;
// 进行窗口内数据的一系列更新
...
}其中 valid 变量表示窗口中满足 need 条件的字符个数,如果 valid 和 need.size 的大小相同,则说明窗口已满足条件,已经完全覆盖了串 T。
现在开始套模板,只需要思考以下几个问题:
1、什么时候应该移动 right 扩大窗口?窗口加入字符时,应该更新哪些数据?
2、什么时候窗口应该暂停扩大,开始移动 left 缩小窗口?从窗口移出字符时,应该更新哪些数据?
3、我们要的结果应该在扩大窗口时还是缩小窗口时进行更新?
如果一个字符进入窗口,应该增加 window 计数器;如果一个字符将移出窗口的时候,应该减少 window 计数器;当 valid 满足 need 时应该收缩窗口;应该在收缩窗口的时候更新最终结果。
下面是完整代码:
class Solution {
public String minWindow(String s, String t) {
Map<Character, Integer> need = new HashMap<>();
Map<Character, Integer> window = new HashMap<>();
for (char c : t.toCharArray()) {
need.put(c, need.getOrDefault(c, 0) + 1);
}
int left = 0, right = 0; int valid = 0;
// 记录最小覆盖子串的起始索引及长度
int start = 0, len = Integer.MAX_VALUE;
while (right < s.length()) {
// c 是将移入窗口的字符
char c = s.charAt(right);
// 扩大窗口
right++;
// 进行窗口内数据的一系列更新
if (need.containsKey(c)) {
window.put(c, window.getOrDefault(c, 0) + 1);
if (window.get(c).equals(need.get(c)))
valid++;
}
// 判断左侧窗口是否要收缩
while (valid == need.size()) {
int valid = 0;
// 记录最小覆盖子串的起始索引及长度
int start = 0, len = Integer.MAX_VALUE;
while (right < s.length()) {
// c 是将移入窗口的字符
char c = s.charAt(right);
// 扩大窗口
right++;
// 进行窗口内数据的一系列更新
if (need.containsKey(c)) {
window.put(c, window.getOrDefault(c, 0) + 1);
if (window.get(c).equals(need.get(c)))
valid++;
}
// 判断左侧窗口是否要收缩
while (valid == need.size()) { // 在这里更新最小覆盖子串
if (right - left < len) {
start = left;
len = right - left;
}
// d 是将移出窗口的字符
char d = s.charAt(left);
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
if (need.containsKey(d)) {
if (window.get(d).equals(need.get(d)))
valid--;
window.put(d, window.get(d) - 1);
}
}
// 在这里更新最小覆盖子串
if (right - left < len) {
start = left;
len = right - left;
}
// d 是将移出窗口的字符
char d = s.charAt(left);
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
if (need.containsKey(d)) {
if (window.get(d).equals(need.get(d)))
valid--;
window.put(d, window.get(d) - 1);
}
} }
// 返回最小覆盖子串
return len == Integer.MAX_VALUE ? "" : s.substring(start, start + len);
}
}
}
// 返回最小覆盖子串
return len == Integer.MAX_VALUE ? "" : s.substring(start, start + len);
}
}class Solution {
public:
string minWindow(string s, string t) {
unordered_map<char, int> need, window;
for (char c : t) {
need[c]++;
}
int left = 0, right = 0;
// 记录window中的字符满足need条件的字符个数
int valid = 0;
// 记录最小覆盖子串的起始索引及长度
int start = 0, len = INT_MAX;
while (right < s.size()) {
// c 是将移入窗口的字符
char c = s[right];
// 扩大窗口
right++;
// 进行窗口内数据的一系列更新
if (need.count(c)) {
window[c]++;
if (window[c] == need[c])
valid++;
}
// 判断左侧窗口是否要收缩
while (valid == need.size()) { // 在这里更新最小覆盖子串
if (right - left < len) {
start = left;
len = right - left;
}
// d 是将移出窗口的字符
char d = s[left];
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
if (need.count(d)) {
if (window[d] == need[d])
valid--;
window[d]--;
}
}
// 在这里更新最小覆盖子串
if (right - left < len) {
start = left;
len = right - left;
}
// d 是将移出窗口的字符
char d = s[left];
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
if (need.count(d)) {
if (window[d] == need[d])
valid--;
window[d]--;
}
} }
// 返回最小覆盖子串
return len == INT_MAX ? "" : s.substr(start, len);
}
};
}
// 返回最小覆盖子串
return len == INT_MAX ? "" : s.substr(start, len);
}
};class Solution:
def minWindow(self, s: str, t: str) -> str:
need, window = {}, {}
for c in t:
need[c] = need.get(c, 0) + 1
left = 0
right = 0
valid = 0
# 记录最小覆盖子串的起始索引及长度
start = 0
length = float('inf')
while right < len(s):
# c 是将移入窗口的字符
c = s[right]
# 扩大窗口
right += 1
# 进行窗口内数据的一系列更新
if c in need:
window[c] = window.get(c, 0) + 1
if window[c] == need[c]:
valid += 1
# 判断左侧窗口是否要收缩
while valid == len(need):  # 在这里更新最小覆盖子串
if right - left < length:
start = left
length = right - left
# d 是将移出窗口的字符
d = s[left]
# 缩小窗口
left += 1
# 进行窗口内数据的一系列更新
if d in need:
if window[d] == need[d]:
valid -= 1
window[d] -= 1
# 在这里更新最小覆盖子串
if right - left < length:
start = left
length = right - left
# d 是将移出窗口的字符
d = s[left]
# 缩小窗口
left += 1
# 进行窗口内数据的一系列更新
if d in need:
if window[d] == need[d]:
valid -= 1
window[d] -= 1 # 返回最小覆盖子串
return "" if length == float('inf') else s[start: start + length]
# 返回最小覆盖子串
return "" if length == float('inf') else s[start: start + length]func minWindow(s string, t string) string {
need, window := make(map[byte]int), make(map[byte]int)
for i := range t {
need[t[i]]++
}
left, right := 0, 0
valid := 0
// 记录最小覆盖子串的起始索引及长度
start, length := 0, math.MaxInt32
for right < len(s) {
// c 是将移入窗口的字符
c := s[right]
// 扩大窗口
right++
// 进行窗口内数据的一系列更新
if _, ok := need[c]; ok {
window[c]++
if window[c] == need[c] {
valid++
}
}
// 判断左侧窗口是否要收缩
for valid == len(need) { // 在这里更新最小覆盖子串
if right - left < length {
start = left
length = right - left
}
// d 是将移出窗口的字符
d := s[left]
// 缩小窗口
left++
// 进行窗口内数据的一系列更新
if _, ok := need[d]; ok {
if window[d] == need[d] {
valid--
}
window[d]--
}
}
// 在这里更新最小覆盖子串
if right - left < length {
start = left
length = right - left
}
// d 是将移出窗口的字符
d := s[left]
// 缩小窗口
left++
// 进行窗口内数据的一系列更新
if _, ok := need[d]; ok {
if window[d] == need[d] {
valid--
}
window[d]--
}
} }
// 返回最小覆盖子串
if length == math.MaxInt32 {
return ""
}
return s[start : start+length]
}
}
// 返回最小覆盖子串
if length == math.MaxInt32 {
return ""
}
return s[start : start+length]
}var minWindow = function(s, t) {
let need = {}, window = {};
for (let c of t) {
need[c] = (need[c] || 0) + 1;
}
let left = 0, right = 0;
let valid = 0;
// 记录最小覆盖子串的起始索引及长度
let start = 0, len = Infinity;
while (right < s.length) {
// c 是将移入窗口的字符
let c = s[right];
// 扩大窗口
right++;
// 进行窗口内数据的一系列更新
if (need[c]) {
window[c] = (window[c] || 0) + 1;
if (window[c] === need[c]) {
valid++;
}
}
// 判断左侧窗口是否要收缩
while (valid === Object.keys(need).length) { // 在这里更新最小覆盖子串
if (right - left < len) {
start = left;
len = right - left;
}
// d 是将移出窗口的字符
let d = s[left];
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
if (need[d]) {
if (window[d] === need[d]) {
valid--;
}
window[d]--;
}
// 在这里更新最小覆盖子串
if (right - left < len) {
start = left;
len = right - left;
}
// d 是将移出窗口的字符
let d = s[left];
// 缩小窗口
left++;
// 进行窗口内数据的一系列更新
if (need[d]) {
if (window[d] === need[d]) {
valid--;
}
window[d]--;
} }
}
// 返回最小覆盖子串
return len === Infinity ? "" : s.substring(start, start + len);
};
}
}
// 返回最小覆盖子串
return len === Infinity ? "" : s.substring(start, start + len);
};你可以点开下面的可视化面板,多次点击 while (right < s.length) 这一行代码,即可看到滑动窗口 [left, right) 的滑动过程:
算法可视化面板
使用 Java 的读者请注意
对 Java 包装类进行比较时要尤为小心,Integer,String 等类型应该用 equals 方法判定相等,而不能直接用等号 ==,否则会出错。所以在缩小窗口更新数据的时候,不能直接写为 window.get(d) == need.get(d),而要用 window.get(d).equals(need.get(d)),之后的题目代码同理。
上面的代码中,当我们发现某个字符在 window 的数量满足了 need 的需要,就要更新 valid,表示有一个字符已经满足要求。而且,你能发现,两次对窗口内数据的更新操作是完全对称的。
当 valid == need.size() 时,说明 T 中所有字符已经被覆盖,已经得到一个可行的覆盖子串,现在应该开始收缩窗口了,以便得到「最小覆盖子串」。
移动 left 收缩窗口时,窗口内的字符都是可行解,所以应该在收缩窗口的阶段进行最小覆盖子串的更新,以便从可行解中找到长度最短的最终结果。
至此,应该可以完全理解这套框架了,滑动窗口算法又不难,就是细节问题让人烦得很。以后遇到滑动窗口算法,你就按照这框架写代码,保准没有 bug,还省事儿。
下面就直接利用这套框架秒杀几道题吧,你基本上一眼就能看出思路了。
二、字符串排列
这是力扣第 567 题「字符串的排列」,难度中等:
567. 字符串的排列 | 力扣 | LeetCode | 🟠
给你两个字符串 s1 和 s2 ,写一个函数来判断 s2 是否包含 s1 的排列。如果是,返回 true ;否则,返回 false 。
换句话说,s1 的排列之一是 s2 的 子串 。
示例 1:
输入:s1 = "ab" s2 = "eidbaooo"
输出:true
解释:s2 包含 s1 的排列之一 ("ba").
示例 2:
输入:s1= "ab" s2 = "eidboaoo" 输出:false
提示:
1 <= s1.length, s2.length <= 104s1和s2仅包含小写字母
注意哦,输入的 s1 是可以包含重复字符的,所以这个题难度不小。
这种题目,是明显的滑动窗口算法,相当给你一个 S 和一个 T,请问你 S 中是否存在一个和 T 长度相同的子串,且包含 T 中所有字符?
首先,先复制粘贴之前的算法框架代码,然后明确刚才提出的几个问题,即可写出这道题的答案:
class Solution {
// 判断 s 中是否存在 t 的排列
public boolean checkInclusion(String t, String s) {
Map<Character, Integer> need = new HashMap<>();
Map<Character, Integer> window = new HashMap<>();
for (char c : t.toCharArray()) need.put(c, need.getOrDefault(c, 0) + 1);
int left = 0, right = 0;
int valid = 0;
while (right < s.length()) {
char c = s.charAt(right);
right++;
// 进行窗口内数据的一系列更新
if (need.containsKey(c)) {
window.put(c, window.getOrDefault(c, 0) + 1);
if (window.get(c).equals(need.get(c)))
valid++;
}
// 判断左侧窗口是否要收缩
while (right - left >= t.length()) {
// 在这里判断是否找到了合法的子串
if (valid == need.size())
return true;
char d = s.charAt(left);
left++;
// 进行窗口内数据的一系列更新
if (need.containsKey(d)) {
if (window.get(d).equals(need.get(d)))
valid--;
window.put(d, window.get(d) - 1);
}
}
}
// 未找到符合条件的子串
return false;
}
}class Solution {
public:
// 判断 s 中是否存在 t 的排列
bool checkInclusion(string t, string s) {
unordered_map<char, int> need, window;
for (char c : t) need[c]++;
int left = 0, right = 0;
int valid = 0;
while (right < s.size()) {
char c = s[right];
right++;
// 进行窗口内数据的一系列更新
if (need.count(c)) {
window[c]++;
if (window[c] == need[c])
valid++;
}
// 判断左侧窗口是否要收缩
while (right - left >= t.size()) {
// 在这里判断是否找到了合法的子串
if (valid == need.size())
return true;
char d = s[left];
left++;
// 进行窗口内数据的一系列更新
if (need.count(d)) {
if (window[d] == need[d])
valid--;
window[d]--;
}
}
}
// 未找到符合条件的子串
return false;
}
};class Solution:
# 判断 s 中是否存在 t 的排列
def checkInclusion(self, t: str, s: str) -> bool:
need = {}
window = {}
for c in t:
need[c] = need.get(c, 0) + 1
left = 0
right = 0
valid = 0
while right < len(s):
c = s[right]
right += 1
# 进行窗口内数据的一系列更新
if c in need:
window[c] = window.get(c, 0) + 1
if window[c] == need[c]:
valid += 1
# 判断左侧窗口是否要收缩
while right - left >= len(t):
# 在这里判断是否找到了合法的子串
if valid == len(need):
return True
d = s[left]
left += 1
# 进行窗口内数据的一系列更新
if d in need:
if window[d] == need[d]:
valid -= 1
window[d] -= 1
# 未找到符合条件的子串
return Falsefunc checkInclusion(t string, s string) bool {
// 判断 s 中是否存在 t 的排列
need := make(map[rune]int)
window := make(map[rune]int)
for _, c := range t {
need[c]++
}
left, right := 0, 0
valid := 0
for right < len(s) {
c := rune(s[right])
right++
// 进行窗口内数据的一系列更新
if need[c] > 0 {
window[c]++
if window[c] == need[c] {
valid++
}
}
// 判断左侧窗口是否要收缩
for right-left >= len(t) {
// 在这里判断是否找到了合法的子串
if valid == len(need) {
return true
}
d := rune(s[left])
left++
// 进行窗口内数据的一系列更新
if need[d] > 0 {
if window[d] == need[d] {
valid--
}
window[d]--
}
}
}
// 未找到符合条件的子串
return false
}var checkInclusion = function(t, s) {
// 判断 s 中是否存在 t 的排列
let need = new Map();
let window = new Map();
for (let c of t) {
need.set(c, (need.get(c) || 0) + 1);
}
let left = 0, right = 0;
let valid = 0;
while (right < s.length) {
let c = s.charAt(right);
right++;
// 进行窗口内数据的一系列更新
if (need.has(c)) {
window.set(c, (window.get(c) || 0) + 1);
if (window.get(c) === need.get(c)) {
valid++;
}
}
// 判断左侧窗口是否要收缩
while (right - left >= t.length) {
// 在这里判断是否找到了合法的子串
if (valid === need.size) {
return true;
}
let d = s.charAt(left);
left++;
// 进行窗口内数据的一系列更新
if (need.has(d)) {
if (window.get(d) === need.get(d)) {
valid--;
}
window.set(d, window.get(d) - 1);
}
}
}
// 未找到符合条件的子串
return false;
};你可以点开下面的可视化面板,多次点击 while (right < s.length) 这一行代码,即可看到定长窗口滑动的过程:
算法可视化面板
对于这道题的解法代码,基本上和最小覆盖子串一模一样,只需要改变几个地方:
1、本题移动 left 缩小窗口的时机是窗口大小大于 t.length() 时,因为排列嘛,显然长度应该是一样的。
2、当发现 valid == need.size() 时,就说明窗口中就是一个合法的排列,所以立即返回 true。
至于如何处理窗口的扩大和缩小,和最小覆盖子串完全相同。
小优化
由于这道题中 [left, right) 其实维护的是一个定长的窗口,窗口长度为 t.length()。因为定长窗口每次向前滑动时只会移出一个字符,所以完全可以把内层的 while 改成 if,效果是一样的。
三、找所有字母异位词
这是力扣第 438 题「找到字符串中所有字母异位词」,难度中等:
438. 找到字符串中所有字母异位词 | 力扣 | LeetCode | 🟠
给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。
示例 1:
输入: s = "cbaebabacd", p = "abc" 输出: [0,6] 解释: 起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。 起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。
示例 2:
输入: s = "abab", p = "ab" 输出: [0,1,2] 解释: 起始索引等于 0 的子串是 "ab", 它是 "ab" 的异位词。 起始索引等于 1 的子串是 "ba", 它是 "ab" 的异位词。 起始索引等于 2 的子串是 "ab", 它是 "ab" 的异位词。
提示:
1 <= s.length, p.length <= 3 * 104s和p仅包含小写字母
呵呵,这个所谓的字母异位词,不就是排列吗,搞个高端的说法就能糊弄人了吗?相当于,输入一个串 S,一个串 T,找到 S 中所有 T 的排列,返回它们的起始索引。
直接默写一下框架,明确刚才讲的三个问题,即可秒杀这道题:
class Solution {
public List<Integer> findAnagrams(String s, String t) {
Map<Character, Integer> need = new HashMap<>();
Map<Character, Integer> window = new HashMap<>();
for (char c : t.toCharArray()) {
need.put(c, need.getOrDefault(c, 0) + 1);
}
int left = 0, right = 0;
int valid = 0;
// 记录结果
List<Integer> res = new ArrayList<>();
while (right < s.length()) {
char c = s.charAt(right);
right++;
// 进行窗口内数据的一系列更新
if (need.containsKey(c)) {
window.put(c, window.getOrDefault(c, 0) + 1);
if (window.get(c).equals(need.get(c))) {
valid++;
}
}
// 判断左侧窗口是否要收缩
while (right - left >= t.length()) {
// 当窗口符合条件时,把起始索引加入 res
if (valid == need.size()) {
res.add(left);
}
char d = s.charAt(left);
left++;
// 进行窗口内数据的一系列更新
if (need.containsKey(d)) {
if (window.get(d).equals(need.get(d))) {
valid--;
}
window.put(d, window.get(d) - 1);
}
}
}
return res;
}
}#include <vector>
#include <string>
#include <unordered_map>
using namespace std;
class Solution {
public:
vector<int> findAnagrams(string s, string t) {
unordered_map<char, int> need;
unordered_map<char, int> window;
for (char c : t) {
need[c]++;
}
int left = 0, right = 0;
int valid = 0;
// 记录结果
vector<int> res;
while (right < s.size()) {
char c = s[right];
right++;
// 进行窗口内数据的一系列更新
if (need.count(c)) {
window[c]++;
if (window[c] == need[c]) {
valid++;
}
}
// 判断左侧窗口是否要收缩
while (right - left >= t.size()) {
// 当窗口符合条件时,把起始索引加入 res
if (valid == need.size()) {
res.push_back(left);
}
char d = s[left];
left++;
// 进行窗口内数据的一系列更新
if (need.count(d)) {
if (window[d] == need[d]) {
valid--;
}
window[d]--;
}
}
}
return res;
}
};class Solution:
def findAnagrams(self, s: str, t: str) -> list[int]:
need = {}
window = {}
for c in t:
need[c] = need.get(c, 0) + 1
left = 0
right = 0
valid = 0
# 记录结果
res = []
while right < len(s):
c = s[right]
right += 1
# 进行窗口内数据的一系列更新
if c in need:
window[c] = window.get(c, 0) + 1
if window[c] == need[c]:
valid += 1
# 判断左侧窗口是否要收缩
while right - left >= len(t):
# 当窗口符合条件时,把起始索引加入 res
if valid == len(need):
res.append(left)
d = s[left]
left += 1
# 进行窗口内数据的一系列更新
if d in need:
if window[d] == need[d]:
valid -= 1
window[d] -= 1
return resfunc findAnagrams(s string, t string) []int {
need := make(map[rune]int)
window := make(map[rune]int)
for _, c := range t {
need[c] = need[c] + 1
}
left, right, valid := 0, 0, 0
// 记录结果
res := []int{}
for right < len(s) {
c := rune(s[right])
right++
// 进行窗口内数据的一系列更新
if _, ok := need[c]; ok {
window[c] = window[c] + 1
if window[c] == need[c] {
valid++
}
}
// 判断左侧窗口是否要收缩
for right-left >= len(t) {
// 当窗口符合条件时,把起始索引加入 res
if valid == len(need) {
res = append(res, left)
}
d := rune(s[left])
left++
// 进行窗口内数据的一系列更新
if _, ok := need[d]; ok {
if window[d] == need[d] {
valid--
}
window[d] = window[d] - 1
}
}
}
return res
}var findAnagrams = function(s, t) {
let need = new Map();
let window = new Map();
for (let c of t) {
need.set(c, (need.get(c) || 0) + 1);
}
let left = 0, right = 0;
let valid = 0;
// 记录结果
let res = [];
while (right < s.length) {
let c = s[right];
right++;
// 进行窗口内数据的一系列更新
if (need.has(c)) {
window.set(c, (window.get(c) || 0) + 1);
if (window.get(c) === need.get(c)) {
valid++;
}
}
// 判断左侧窗口是否要收缩
while (right - left >= t.length) {
// 当窗口符合条件时,把起始索引加入 res
if (valid === need.size) {
res.push(left);
}
let d = s[left];
left++;
// 进行窗口内数据的一系列更新
if (need.has(d)) {
if (window.get(d) === need.get(d)) {
valid--;
}
window.set(d, window.get(d) - 1);
}
}
}
return res;
};跟寻找字符串的排列一样,只是找到一个合法异位词(排列)之后将起始索引加入 res 即可。
你可以点开下面的可视化面板,多次点击 while (right < s.length) 这一行代码,即可看到定长窗口滑动的过程:
算法可视化面板
四、最长无重复子串
这是力扣第 3 题「无重复字符的最长子串」,难度中等:
3. 无重复字符的最长子串 | 力扣 | LeetCode | 🟠
给定一个字符串 s ,请你找出其中不含有重复字符的 最长 子串 的长度。
示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
输入: s = "pwwkew" 输出: 3 解释: 因为无重复字符的最长子串是"wke",所以其长度为 3。 请注意,你的答案必须是 子串 的长度,"pwke"是一个子序列,不是子串。
提示:
0 <= s.length <= 5 * 104s由英文字母、数字、符号和空格组成
这个题终于有了点新意,不是一套框架就出答案,不过反而更简单了,稍微改一改框架就行了:
class Solution {
public int lengthOfLongestSubstring(String s) {
Map<Character, Integer> window = new HashMap<>();
int left = 0, right = 0;
// 记录结果
int res = 0;
while (right < s.length()) {
char c = s.charAt(right);
right++;
// 进行窗口内数据的一系列更新
window.put(c, window.getOrDefault(c, 0) + 1);
// 判断左侧窗口是否要收缩
while (window.get(c) > 1) {
char d = s.charAt(left);
left++;
// 进行窗口内数据的一系列更新
window.put(d, window.get(d) - 1);
}
// 在这里更新答案
res = Math.max(res, right - left);
}
return res;
}
}class Solution {
public:
int lengthOfLongestSubstring(string s) {
unordered_map<char, int> window;
int left = 0, right = 0;
// 记录结果
int res = 0;
while (right < s.size()) {
char c = s[right];
right++;
// 进行窗口内数据的一系列更新
window[c]++;
// 判断左侧窗口是否要收缩
while (window[c] > 1) {
char d = s[left];
left++;
// 进行窗口内数据的一系列更新
window[d]--;
}
// 在这里更新答案
res = max(res, right - left);
}
return res;
}
};class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
window = {}
left = 0
right = 0
# 记录结果
res = 0
while right < len(s):
c = s[right]
right += 1
# 进行窗口内数据的一系列更新
window[c] = window.get(c, 0) + 1
# 判断左侧窗口是否要收缩
while window[c] > 1:
d = s[left]
left += 1
# 进行窗口内数据的一系列更新
window[d] = window.get(d, 0) - 1
# 在这里更新答案
res = max(res, right - left)
return resfunc lengthOfLongestSubstring(s string) int {
window := make(map[rune]int)
left, right := 0, 0
// 记录结果
res := 0
for right < len(s) {
c := rune(s[right])
right++
// 进行窗口内数据的一系列更新
window[c] = window[c] + 1
// 判断左侧窗口是否要收缩
for window[c] > 1 {
d := rune(s[left])
left++
// 进行窗口内数据的一系列更新
window[d] = window[d] - 1
}
// 在这里更新答案
if res < right-left {
res = right - left
}
}
return res
}var lengthOfLongestSubstring = function(s) {
let window = new Map();
let left = 0, right = 0;
// 记录结果
let res = 0;
while (right < s.length) {
let c = s.charAt(right);
right++;
// 进行窗口内数据的一系列更新
window.set(c, (window.get(c) || 0) + 1);
// 判断左侧窗口是否要收缩
while (window.get(c) > 1) {
let d = s.charAt(left);
left++;
// 进行窗口内数据的一系列更新
window.set(d, window.get(d) - 1);
}
// 在这里更新答案
res = Math.max(res, right - left);
}
return res;
};你可以点开下面的可视化面板,多次点击 while (right < s.length) 这一行代码,即可看到窗口滑动更新答案的过程:
算法可视化面板
这就是变简单了,连 need 和 valid 都不需要,而且更新窗口内数据也只需要简单的更新计数器 window 即可。
当 window[c] 值大于 1 时,说明窗口中存在重复字符,不符合条件,就该移动 left 缩小窗口了嘛。
唯一需要注意的是,在哪里更新结果 res 呢?我们要的是最长无重复子串,哪一个阶段可以保证窗口中的字符串是没有重复的呢?
这里和之前不一样,要在收缩窗口完成后更新 res,因为窗口收缩的 while 条件是存在重复元素,换句话说收缩完成后一定保证窗口中没有重复嘛。
好了,滑动窗口算法模板就讲到这里,希望大家能理解其中的思想,记住算法模板并融会贯通。回顾一下,遇到子数组/子串相关的问题,你只要能回答出来以下几个问题,就能运用滑动窗口算法:
1、什么时候应该扩大窗口?
2、什么时候应该缩小窗口?
3、什么时候应该更新答案?
我在 滑动窗口经典习题 中使用这套思维模式列举了更多经典的习题,旨在强化你对算法的理解和记忆,以后就再也不怕子串、子数组问题了。