216. 组合总和 III https://leetcode.cn/problems/combination-sum-iii
216. Combination Sum III https://leetcode.com/problems/combination-sum-iii
39. 组合总和 https://leetcode.cn/problems/combination-sum
39. Combination Sum https://leetcode.com/problems/combination-sum
40. 组合总和 II https://leetcode.cn/problems/combination-sum-ii
40. Combination Sum II https://leetcode.com/problems/combination-sum-ii
46. 全排列 https://leetcode.cn/problems/permutations
46. Permutations https://leetcode.com/problems/permutations
47. 全排列 II https://leetcode.cn/problems/permutations-ii
47. Permutations II https://leetcode.com/problems/permutations-ii
77. 组合 https://leetcode.cn/problems/combinations
77. Combinations https://leetcode.com/problems/combinations
78. 子集 https://leetcode.cn/problems/subsets
78. Subsets https://leetcode.com/problems/subsets
90. 子集 II https://leetcode.cn/problems/subsets-ii
90. Subsets II https://leetcode.com/problems/subsets-ii
剑指 Offer II 082. 含有重复元素集合的组合 https://leetcode.cn/problems/4sjJUc
剑指 Offer II 082. 含有重复元素集合的组合 https://leetcode.com/problems/4sjJUc
剑指 Offer II 084. 含有重复元素集合的全排列 https://leetcode.cn/problems/7p8L0Z
剑指 Offer II 084. 含有重复元素集合的全排列 https://leetcode.com/problems/7p8L0Z
虽然排列、组合、子集系列问题是高中就学过的，但如果想编写算法解决它们，还是非常考验计算机思维的，本文就讲讲编程解决这几个问题的核心思路，以后再有什么变体，你也能手到擒来，以不变应万变。
无论是排列、组合还是子集问题，简单说无非就是让你从序列 nums 中以给定规则取若干元素，主要有以下几种变体：
形式一、元素无重不可复选，即 nums 中的元素都是唯一的，每个元素最多只能被使用一次，这也是最基本的形式。
以组合为例，如果输入 nums = [2,3,6,7]，和为 7 的组合应该只有 [7]。
形式二、元素可重不可复选，即 nums 中的元素可以存在重复，每个元素最多只能被使用一次。
以组合为例，如果输入 nums = [2,5,2,1,2]，和为 7 的组合应该有两种 [2,2,2,1] 和 [5,2]。
形式三、元素无重可复选，即 nums 中的元素都是唯一的，每个元素可以被使用若干次。
以组合为例，如果输入 nums = [2,3,6,7]，和为 7 的组合应该有两种 [2,2,3] 和 [7]。
当然，也可以说有第四种形式，即元素可重可复选。但既然元素可复选，那又何必存在重复元素呢？元素去重之后就等同于形式三，所以这种情况不用考虑。
上面用组合问题举的例子，但排列、组合、子集问题都可以有这三种基本形式，所以共有 9 种变化。
除此之外，题目也可以再添加各种限制条件，比如让你求和为 target 且元素个数为 k 的组合，那这么一来又可以衍生出一堆变体，怪不得面试笔试中经常考到排列组合这种基本题型。
但无论形式怎么变化，其本质就是穷举所有解，而这些解呈现树形结构，所以合理使用回溯算法框架，稍改代码框架即可把这些问题一网打尽。
具体来说，你需要先阅读并理解前文 回溯算法核心套路，然后记住如下子集问题和排列问题的回溯树，就可以解决所有排列组合子集相关的问题：
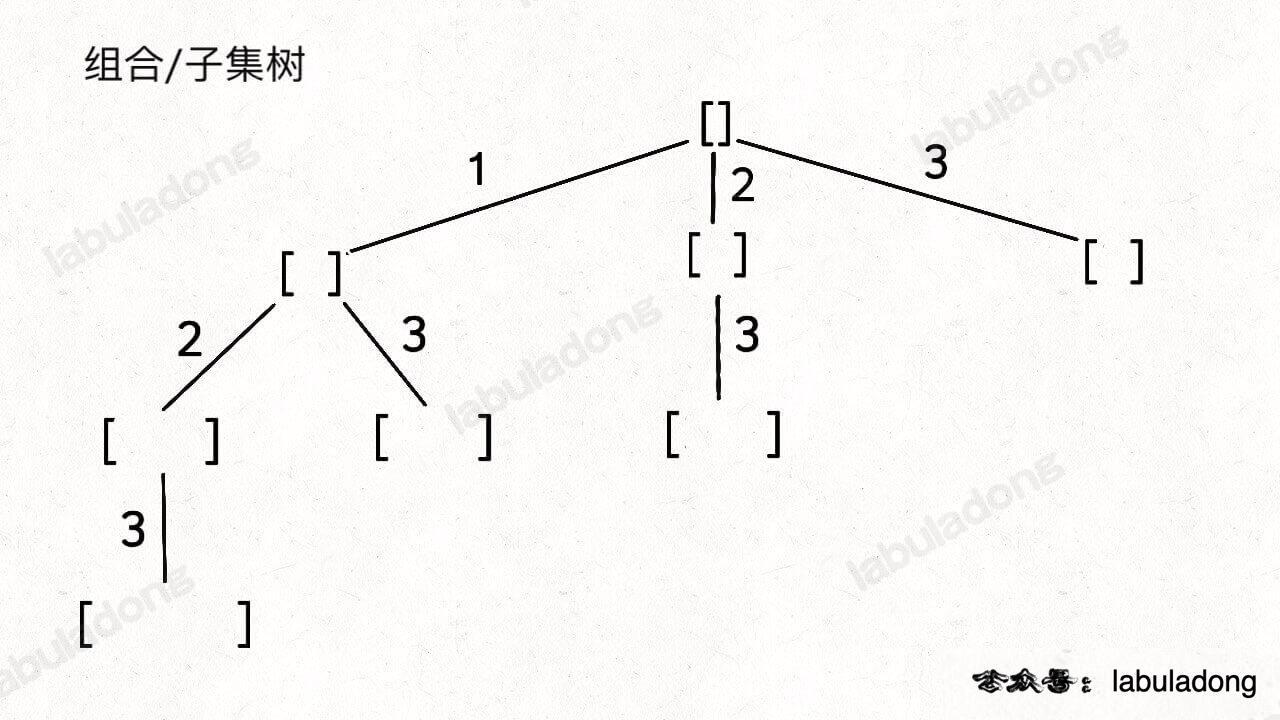
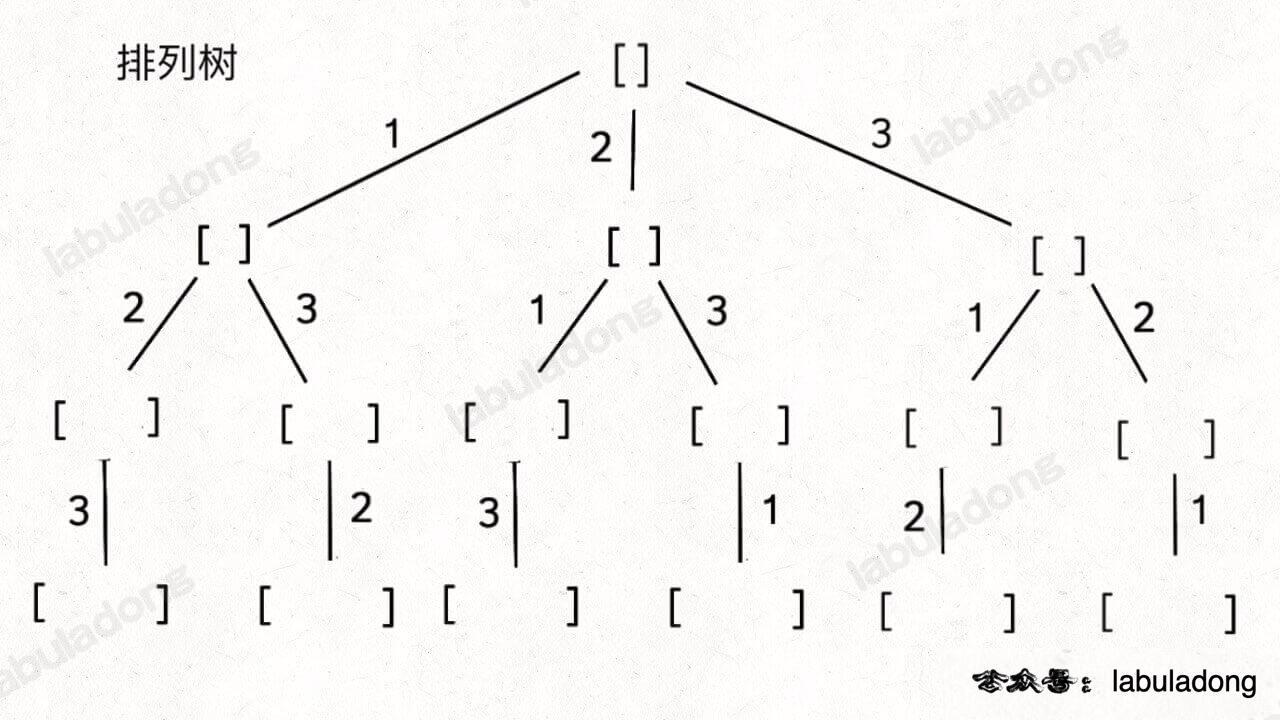
为什么只要记住这两种树形结构就能解决所有相关问题呢？
首先，组合问题和子集问题其实是等价的，这个后面会讲；至于之前说的三种变化形式，无非是在这两棵树上剪掉或者增加一些树枝罢了。
那么，接下来我们就开始穷举，把排列/组合/子集问题的 9 种形式都过一遍，学学如何用回溯算法把它们一套带走。
提示
另外，有些读者之前看过的排列/子集/组合的解法代码可能和我在本文介绍的代码不同。这是因为回溯算法有两种穷举视角，我会在后文 球盒模型：回溯算法穷举的两种视角 手把手给你讲清楚。现在还不适合直接跟你讲那些解法，你照着我的思路学习即可。
子集（元素无重不可复选）
组合（元素无重不可复选）
排列（元素无重不可复选）
子集/组合（元素可重不可复选）
排列（元素可重不可复选）
子集/组合（元素无重可复选）
排列（元素无重可复选）
最后总结
