双指针技巧秒杀七道链表题目
本文讲解的例题
视频讲解
本文总结一下单链表的基本技巧,每个技巧都对应着至少一道算法题:
1、合并两个有序链表
2、链表的分解
3、合并 k 个有序链表
4、寻找单链表的倒数第 k 个节点
5、寻找单链表的中点
6、判断单链表是否包含环并找出环起点
7、判断两个单链表是否相交并找出交点
这些解法都用到了双指针技巧,所以说对于单链表相关的题目,双指针的运用是非常广泛的,下面我们就来一个一个看。
合并两个有序链表
这是最基本的链表技巧,力扣第 21 题「合并两个有序链表」就是这个问题,给你输入两个有序链表,请你把他俩合并成一个新的有序链表:
21. 合并两个有序链表 | 力扣 | LeetCode | 🟢
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例 1:
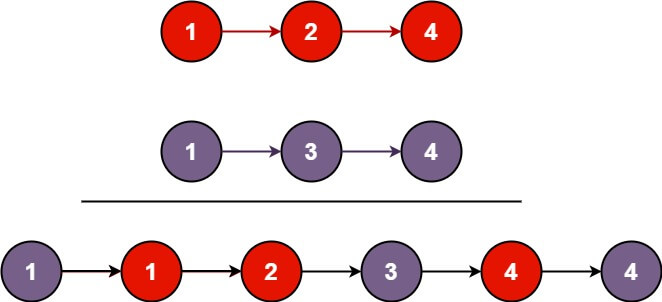
输入:l1 = [1,2,4], l2 = [1,3,4] 输出:[1,1,2,3,4,4]
示例 2:
输入:l1 = [], l2 = [] 输出:[]
示例 3:
输入:l1 = [], l2 = [0] 输出:[0]
提示:
- 两个链表的节点数目范围是
[0, 50] -100 <= Node.val <= 100l1和l2均按 非递减顺序 排列
// 函数签名如下
ListNode mergeTwoLists(ListNode l1, ListNode l2);// 函数签名如下
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2);# 函数签名如下
def mergeTwoLists(l1: ListNode, l2: ListNode) -> ListNode:// 函数签名如下
func mergeTwoLists(l1 *ListNode, l2 *ListNode) *ListNode {}// 函数签名如下
var mergeTwoLists = function(l1, l2) {}这题比较简单,我们直接看解法:
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
// 虚拟头结点
ListNode dummy = new ListNode(-1), p = dummy;
ListNode p1 = l1, p2 = l2;
while (p1 != null && p2 != null) { // 比较 p1 和 p2 两个指针
// 将值较小的的节点接到 p 指针
if (p1.val > p2.val) {
p.next = p2;
p2 = p2.next;
} else {
p.next = p1;
p1 = p1.next;
}
// p 指针不断前进
p = p.next;
}
if (p1 != null) {
p.next = p1;
}
if (p2 != null) {
p.next = p2;
}
return dummy.next;
}
}
// 比较 p1 和 p2 两个指针
// 将值较小的的节点接到 p 指针
if (p1.val > p2.val) {
p.next = p2;
p2 = p2.next;
} else {
p.next = p1;
p1 = p1.next;
}
// p 指针不断前进
p = p.next;
}
if (p1 != null) {
p.next = p1;
}
if (p2 != null) {
p.next = p2;
}
return dummy.next;
}
}class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
// 虚拟头结点
ListNode dummy(-1), *p = &dummy;
ListNode *p1 = l1, *p2 = l2;
while (p1 != nullptr && p2 != nullptr) { // 比较 p1 和 p2 两个指针
// 将值较小的的节点接到 p 指针
if (p1->val > p2->val) {
p->next = p2;
p2 = p2->next;
} else {
p->next = p1;
p1 = p1->next;
}
// p 指针不断前进
p = p->next;
}
if (p1 != nullptr) {
p->next = p1;
}
if (p2 != nullptr) {
p->next = p2;
}
return dummy.next;
}
};
// 比较 p1 和 p2 两个指针
// 将值较小的的节点接到 p 指针
if (p1->val > p2->val) {
p->next = p2;
p2 = p2->next;
} else {
p->next = p1;
p1 = p1->next;
}
// p 指针不断前进
p = p->next;
}
if (p1 != nullptr) {
p->next = p1;
}
if (p2 != nullptr) {
p->next = p2;
}
return dummy.next;
}
};class Solution:
def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
# 虚拟头结点
dummy = ListNode(-1)
p = dummy
p1 = l1
p2 = l2
while p1 is not None and p2 is not None:  # 比较 p1 和 p2 两个指针
# 将值较小的的节点接到 p 指针
if p1.val > p2.val:
p.next = p2
p2 = p2.next
else:
p.next = p1
p1 = p1.next
# p 指针不断前进
p = p.next
if p1 is not None:
p.next = p1
if p2 is not None:
p.next = p2
return dummy.next
# 比较 p1 和 p2 两个指针
# 将值较小的的节点接到 p 指针
if p1.val > p2.val:
p.next = p2
p2 = p2.next
else:
p.next = p1
p1 = p1.next
# p 指针不断前进
p = p.next
if p1 is not None:
p.next = p1
if p2 is not None:
p.next = p2
return dummy.nextfunc mergeTwoLists(l1 *ListNode, l2 *ListNode) *ListNode {
// 虚拟头结点
dummy := &ListNode{-1, nil}
p := dummy
p1 := l1
p2 := l2
for p1 != nil && p2 != nil { // 比较 p1 和 p2 两个指针
// 将值较小的的节点接到 p 指针
if p1.Val > p2.Val {
p.Next = p2
p2 = p2.Next
} else {
p.Next = p1
p1 = p1.Next
}
// p 指针不断前进
p = p.Next
}
if p1 != nil {
p.Next = p1
}
if p2 != nil {
p.Next = p2
}
return dummy.Next
}
// 比较 p1 和 p2 两个指针
// 将值较小的的节点接到 p 指针
if p1.Val > p2.Val {
p.Next = p2
p2 = p2.Next
} else {
p.Next = p1
p1 = p1.Next
}
// p 指针不断前进
p = p.Next
}
if p1 != nil {
p.Next = p1
}
if p2 != nil {
p.Next = p2
}
return dummy.Next
}var mergeTwoLists = function(l1, l2) {
// 虚拟头结点
var dummy = new ListNode(-1), p = dummy;
var p1 = l1, p2 = l2;
while (p1 !== null && p2 !== null) { // 比较 p1 和 p2 两个指针
// 将值较小的的节点接到 p 指针
if (p1.val > p2.val) {
p.next = p2;
p2 = p2.next;
} else {
p.next = p1;
p1 = p1.next;
}
// p 指针不断前进
p = p.next;
}
if (p1 !== null) {
p.next = p1;
}
if (p2 !== null) {
p.next = p2;
}
return dummy.next;
};
// 比较 p1 和 p2 两个指针
// 将值较小的的节点接到 p 指针
if (p1.val > p2.val) {
p.next = p2;
p2 = p2.next;
} else {
p.next = p1;
p1 = p1.next;
}
// p 指针不断前进
p = p.next;
}
if (p1 !== null) {
p.next = p1;
}
if (p2 !== null) {
p.next = p2;
}
return dummy.next;
};我们的 while 循环每次比较 p1 和 p2 的大小,把较小的节点接到结果链表上,看如下 GIF:

形象地理解,这个算法的逻辑类似于拉拉链,l1, l2 类似于拉链两侧的锯齿,指针 p 就好像拉链的拉索,将两个有序链表合并。
下面是算法的可视化,你可以多次点击 while (p1 != null && p2 != null) 这一行代码,即可看到 p 合并两个有序链表的过程:
算法可视化面板
代码中还用到一个链表的算法题中是很常见的「虚拟头结点」技巧,也就是 dummy 节点。你可以试试,如果不使用 dummy 虚拟节点,代码会复杂一些,需要额外处理指针 p 为空的情况。而有了 dummy 节点这个占位符,可以避免处理空指针的情况,降低代码的复杂性。
何时使用虚拟头结点
经常有读者问我,什么时候需要用虚拟头结点?我这里总结下:当你需要创造一条新链表的时候,可以使用虚拟头结点简化边界情况的处理。
比如说,让你把两条有序链表合并成一条新的有序链表,是不是要创造一条新链表?再比你想把一条链表分解成两条链表,是不是也在创造新链表?这些情况都可以使用虚拟头结点简化边界情况的处理。
单链表的分解
直接看下力扣第 86 题「分隔链表」:
86. 分隔链表 | 力扣 | LeetCode | 🟠
给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。
你应当 保留 两个分区中每个节点的初始相对位置。
示例 1:
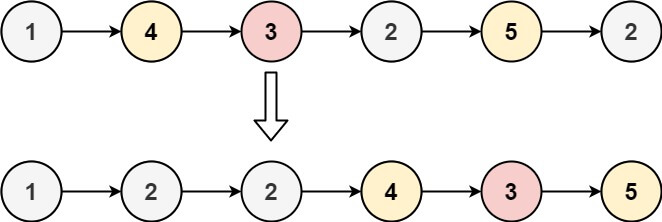
输入:head = [1,4,3,2,5,2], x = 3 输出:[1,2,2,4,3,5]
示例 2:
输入:head = [2,1], x = 2 输出:[1,2]
提示:
- 链表中节点的数目在范围
[0, 200]内 -100 <= Node.val <= 100-200 <= x <= 200
在合并两个有序链表时让你合二为一,而这里需要分解让你把原链表一分为二。具体来说,我们可以把原链表分成两个小链表,一个链表中的元素大小都小于 x,另一个链表中的元素都大于等于 x,最后再把这两条链表接到一起,就得到了题目想要的结果。
整体逻辑和合并有序链表非常相似,细节直接看代码吧,注意虚拟头结点的运用:
class Solution {
public ListNode partition(ListNode head, int x) {
// 存放小于 x 的链表的虚拟头结点
ListNode dummy1 = new ListNode(-1);
// 存放大于等于 x 的链表的虚拟头结点
ListNode dummy2 = new ListNode(-1);
// p1, p2 指针负责生成结果链表
ListNode p1 = dummy1, p2 = dummy2;
// p 负责遍历原链表,类似合并两个有序链表的逻辑
// 这里是将一个链表分解成两个链表
ListNode p = head;
while (p != null) {
if (p.val >= x) {
p2.next = p;
p2 = p2.next;
} else {
p1.next = p;
p1 = p1.next;
}
// 断开原链表中的每个节点的 next 指针
ListNode temp = p.next;
p.next = null;
p = temp;
}
// 链接两个链表
p1.next = dummy2.next;
return dummy1.next;
}
}class Solution {
public:
ListNode* partition(ListNode* head, int x) {
// 存放小于 x 的链表的虚拟头结点
ListNode* dummy1 = new ListNode(-1);
// 存放大于等于 x 的链表的虚拟头结点
ListNode* dummy2 = new ListNode(-1);
// p1, p2 指针负责生成结果链表
ListNode* p1 = dummy1, *p2 = dummy2;
// p 负责遍历原链表,类似合并两个有序链表的逻辑
// 这里是将一个链表分解成两个链表
ListNode* p = head;
while (p != nullptr) {
if (p->val >= x) {
p2->next = p;
p2 = p2->next;
} else {
p1->next = p;
p1 = p1->next;
}
// 不能直接让 p 指针前进,
// p = p->next
// 断开原链表中的每个节点的 next 指针
ListNode* temp = p->next;
p->next = nullptr;
p = temp;
}
// 连接两个链表
p1->next = dummy2->next;
return dummy1->next;
}
};class Solution:
def partition(self, head: ListNode, x: int) -> ListNode:
# 存放小于 x 的链表的虚拟头结点
dummy1 = ListNode(-1)
# 存放大于等于 x 的链表的虚拟头结点
dummy2 = ListNode(-1)
# p1, p2 指针负责生成结果链表
p1, p2 = dummy1, dummy2
# p 负责遍历原链表,类似合并两个有序链表的逻辑
# 这里是将一个链表分解成两个链表
p = head
while p:
if p.val >= x:
p2.next = p
p2 = p2.next
else:
p1.next = p
p1 = p1.next
# 不能直接让 p 指针前进,
# p = p.next
# 断开原链表中的每个节点的 next 指针
temp = p.next
p.next = None
p = temp
# 连接两个链表
p1.next = dummy2.next
return dummy1.nextfunc partition(head *ListNode, x int) *ListNode {
// 存放小于 x 的链表的虚拟头结点
dummy1 := &ListNode{-1, nil}
// 存放大于等于 x 的链表的虚拟头结点
dummy2 := &ListNode{-1, nil}
// p1, p2 指针负责生成结果链表
p1, p2 := dummy1, dummy2
// p 负责遍历原链表,类似合并两个有序链表的逻辑
// 这里是将一个链表分解成两个链表
p := head
for p != nil {
if p.Val >= x {
p2.Next = p
p2 = p2.Next
} else {
p1.Next = p
p1 = p1.Next
}
// 不能直接让 p 指针前进,
// p = p.Next
// 断开原链表中的每个节点的 next 指针
temp := p.Next
p.Next = nil
p = temp
}
// 连接两个链表
p1.Next = dummy2.Next
return dummy1.Next
}var partition = function(head, x) {
// 存放小于 x 的链表的虚拟头结点
let dummy1 = new ListNode(-1);
// 存放大于等于 x 的链表的虚拟头结点
let dummy2 = new ListNode(-1);
// p1, p2 指针负责生成结果链表
let p1 = dummy1, p2 = dummy2;
// p 负责遍历原链表,类似合并两个有序链表的逻辑
// 这里是将一个链表分解成两个链表
let p = head;
while (p !== null) {
if (p.val >= x) {
p2.next = p;
p2 = p2.next;
} else {
p1.next = p;
p1 = p1.next;
}
// 不能直接让 p 指针前进,
// p = p.next
// 断开原链表中的每个节点的 next 指针
let temp = p.next;
p.next = null;
p = temp;
}
// 连接两个链表
p1.next = dummy2.next;
return dummy1.next;
};我知道有很多读者会对这段代码有疑问:
// 不能直接让 p 指针前进,
// p = p.next
// 断开原链表中的每个节点的 next 指针
ListNode temp = p.next;
p.next = null;
p = temp;借助我们的可视化面板看一下就明白了。首先看下正确的写法,你可以多次点击 while (p !== null) 这一行代码即可看到链表分解的过程:
算法可视化面板
如果你不断开原链表中的每个节点的 next 指针,那么就会出错,因为结果链表中会包含一个环,你可以多次点击 while (p !== null) 这一行代码查看:
算法可视化面板
总的来说,如果我们需要把原链表的节点接到新链表上,而不是 new 新节点来组成新链表的话,那么断开节点和原链表之间的链接可能是必要的。那其实我们可以养成一个好习惯,但凡遇到这种情况,就把原链表的节点断开,这样就不会出错了。
合并 k 个有序链表
看下力扣第 23 题「合并K个升序链表」:
23. 合并 K 个升序链表 | 力扣 | LeetCode | 🔴
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例 1:
输入:lists = [[1,4,5],[1,3,4],[2,6]] 输出:[1,1,2,3,4,4,5,6] 解释:链表数组如下: [ 1->4->5, 1->3->4, 2->6 ] 将它们合并到一个有序链表中得到。 1->1->2->3->4->4->5->6
示例 2:
输入:lists = [] 输出:[]
示例 3:
输入:lists = [[]] 输出:[]
提示:
k == lists.length0 <= k <= 10^40 <= lists[i].length <= 500-10^4 <= lists[i][j] <= 10^4lists[i]按 升序 排列lists[i].length的总和不超过10^4
// 函数签名如下
ListNode mergeKLists(ListNode[] lists);// 函数签名如下
ListNode* mergeKLists(vector<ListNode*>& lists);# 函数签名如下
def mergeKLists(lists: List[ListNode]) -> ListNode:// 函数签名如下
func mergeKLists(lists []*ListNode) *ListNode// 函数签名如下
var mergeKLists = function(lists) {};合并 k 个有序链表的逻辑类似合并两个有序链表,难点在于,如何快速得到 k 个节点中的最小节点,接到结果链表上?
这里我们就要用到优先级队列这种数据结构,把链表节点放入一个最小堆,就可以每次获得 k 个节点中的最小节点。关于优先级队列可以参考 优先级队列(二叉堆)原理及实现,本文不展开。
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
if (lists.length == 0) return null;
// 虚拟头结点
ListNode dummy = new ListNode(-1);
ListNode p = dummy;
// 优先级队列,最小堆
PriorityQueue<ListNode> pq = new PriorityQueue<>(
lists.length, (a, b)->(a.val - b.val));
// 将 k 个链表的头结点加入最小堆
for (ListNode head : lists) {
if (head != null)
pq.add(head);
}
while (!pq.isEmpty()) {
// 获取最小节点,接到结果链表中
ListNode node = pq.poll();
p.next = node;
if (node.next != null) {
pq.add(node.next);
}
// p 指针不断前进
p = p.next;
}
return dummy.next;
}
}class Solution {
public:
ListNode* mergeKLists(vector<ListNode*>& lists) {
if (lists.empty()) return nullptr;
// 虚拟头结点
ListNode* dummy = new ListNode(-1);
ListNode* p = dummy;
// 优先级队列,最小堆
auto cmp = [](ListNode* a, ListNode* b) { return a->val > b->val; };
priority_queue<ListNode*, vector<ListNode*>, decltype(cmp)> pq(cmp);
// 将 k 个链表的头结点加入最小堆
for (ListNode* head : lists) {
if (head != nullptr) {
pq.push(head);
}
}
while (!pq.empty()) {
// 获取最小节点,接到结果链表中
ListNode* node = pq.top();
pq.pop();
p->next = node;
if (node->next != nullptr) {
pq.push(node->next);
}
// p 指针不断前进
p = p->next;
}
return dummy->next;
}
};import heapq
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
# 重载比较运算符,方便将 ListNode 加入最小堆
def __lt__(self, other):
return self.val < other.val
class Solution:
def mergeKLists(self, lists):
if not lists:
return None
# 虚拟头结点
dummy = ListNode(-1)
p = dummy
# 优先级队列,最小堆
pq = []
# 将 k 个链表的头结点加入最小堆
for i, head in enumerate(lists):
if head is not None:
heapq.heappush(pq, (head.val, i, head))
while pq:
# 获取最小节点,接到结果链表中
val, i, node = heapq.heappop(pq)
p.next = node
if node.next is not None:
heapq.heappush(pq, (node.next.val, i, node.next))
# p 指针不断前进
p = p.next
return dummy.nextimport "container/heap"
// 为 ListNode 实现 heap.Interface 接口
type PriorityQueue []*ListNode
func (pq PriorityQueue) Len() int { return len(pq) }
func (pq PriorityQueue) Less(i, j int) bool {
return pq[i].Val < pq[j].Val
}
func (pq PriorityQueue) Swap(i, j int) {
pq[i], pq[j] = pq[j], pq[i]
}
func (pq *PriorityQueue) Push(x interface{}) {
*pq = append(*pq, x.(*ListNode))
}
func (pq *PriorityQueue) Pop() interface{} {
old := *pq
n := len(old)
x := old[n-1]
*pq = old[0 : n-1]
return x
}
func mergeKLists(lists []*ListNode) *ListNode {
if len(lists) == 0 {
return nil
}
// 虚拟头结点
dummy := &ListNode{Val: -1}
p := dummy
// 优先级队列,最小堆
pq := &PriorityQueue{}
heap.Init(pq)
// 将 k 个链表的头结点加入最小堆
for _, head := range lists {
if head != nil {
heap.Push(pq, head)
}
}
for pq.Len() > 0 {
// 获取最小节点,接到结果链表中
node := heap.Pop(pq).(*ListNode)
p.Next = node
if node.Next != nil {
heap.Push(pq, node.Next)
}
// p 指针不断前进
p = p.Next
}
return dummy.Next
}var mergeKLists = function(lists) {
if (lists.length === 0) return null;
// 虚拟头结点
var dummy = new ListNode(-1);
var p = dummy;
// 优先级队列,最小堆
var pq = new PriorityQueue((a, b) => a.val - b.val);
// 将 k 个链表的头结点加入最小堆
for (var i = 0; i < lists.length; i++) {
if (lists[i] !== null) {
pq.enqueue(lists[i]);
}
}
while (!pq.isEmpty()) {
// 获取最小节点,接到结果链表中
var node = pq.dequeue();
p.next = node;
if (node.next !== null) {
pq.enqueue(node.next);
}
// p 指针不断前进
p = p.next;
}
return dummy.next;
}你可以点开下面的可视化面板,点击 while (pq.size() > 0) 这一行代码,即可看到有序链表合并的过程:
算法可视化面板
这个算法是面试常考题,它的时间复杂度是多少呢?
优先队列 pq 中的元素个数最多是 ,所以一次 poll 或者 add 方法的时间复杂度是 ;所有的链表节点都会被加入和弹出 pq,所以算法整体的时间复杂度是 ,其中 是链表的条数, 是这些链表的节点总数。
提示
这道题还有一个经典的解法,在 分治算法核心框架 中详细讲解,这里不展开。
单链表的倒数第 k 个节点
从前往后寻找单链表的第 k 个节点很简单,一个 for 循环遍历过去就找到了,但是如何寻找从后往前数的第 k 个节点呢?
那你可能说,假设链表有 n 个节点,倒数第 k 个节点就是正数第 n - k + 1 个节点,不也是一个 for 循环的事儿吗?
是的,但是算法题一般只给你一个 ListNode 头结点代表一条单链表,你不能直接得出这条链表的长度 n,而需要先遍历一遍链表算出 n 的值,然后再遍历链表计算第 n - k + 1 个节点。
也就是说,这个解法需要遍历两次链表才能得到出倒数第 k 个节点。
那么,我们能不能只遍历一次链表,就算出倒数第 k 个节点?可以做到的,如果是面试问到这道题,面试官肯定也是希望你给出只需遍历一次链表的解法。
这个解法就比较巧妙了,假设 k = 2,思路如下:
首先,我们先让一个指针 p1 指向链表的头节点 head,然后走 k 步:
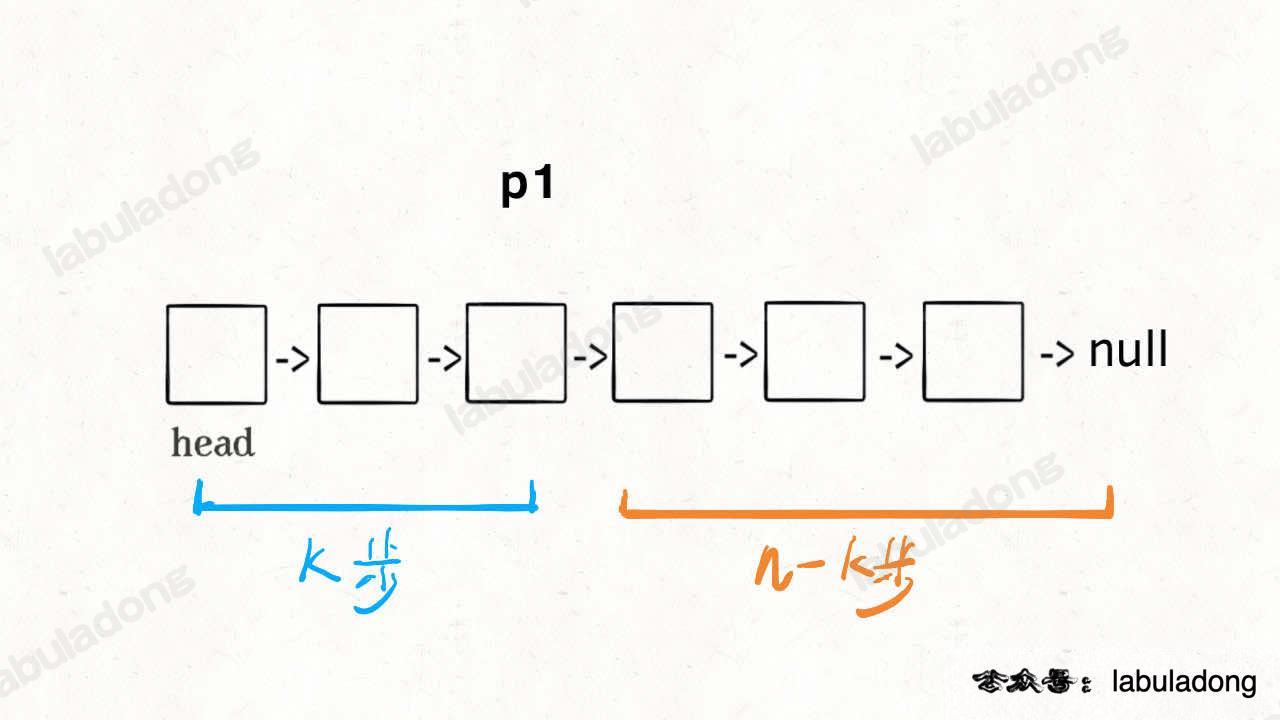
现在的 p1,只要再走 n - k 步,就能走到链表末尾的空指针了对吧?
趁这个时候,再用一个指针 p2 指向链表头节点 head:
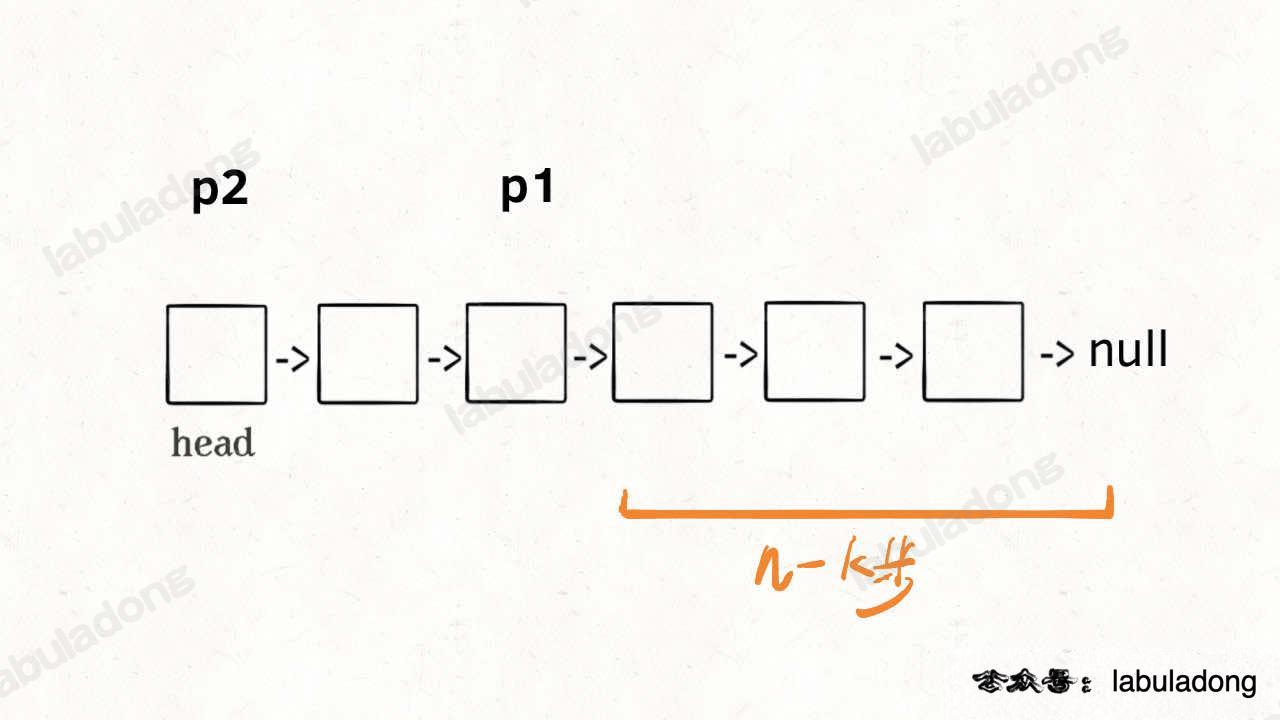
接下来就很显然了,让 p1 和 p2 同时向前走,p1 走到链表末尾的空指针时前进了 n - k 步,p2 也从 head 开始前进了 n - k 步,停留在第 n - k + 1 个节点上,即恰好停链表的倒数第 k 个节点上:
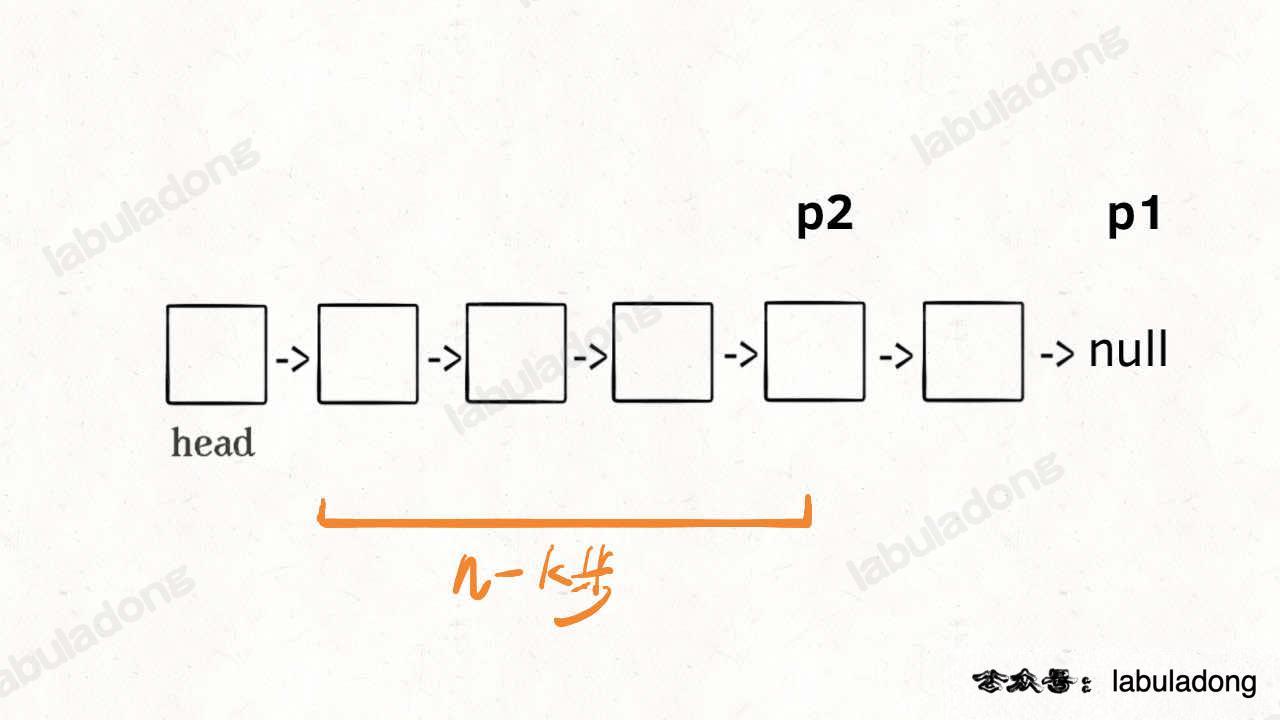
这样,只遍历了一次链表,就获得了倒数第 k 个节点 p2。
上述逻辑的代码如下:
// 返回链表的倒数第 k 个节点
ListNode findFromEnd(ListNode head, int k) {
ListNode p1 = head;
// p1 先走 k 步
for (int i = 0; i < k; i++) {
p1 = p1.next;
}
ListNode p2 = head;
// p1 和 p2 同时走 n - k 步
while (p1 != null) {
p2 = p2.next;
p1 = p1.next;
}
// p2 现在指向第 n - k + 1 个节点,即倒数第 k 个节点
return p2;
}// 返回链表的倒数第 k 个节点
ListNode* findFromEnd(ListNode* head, int k) {
ListNode* p1 = head;
// p1 先走 k 步
for (int i = 0; i < k; i++) {
p1 = p1 -> next;
}
ListNode* p2 = head;
// p1 和 p2 同时走 n - k 步
while (p1 != nullptr) {
p2 = p2 -> next;
p1 = p1 -> next;
}
// p2 现在指向第 n - k + 1 个节点,即倒数第 k 个节点
return p2;
}# 返回链表的倒数第 k 个节点
def findFromEnd(head: ListNode, k: int) -> ListNode:
p1 = head
# p1 先走 k 步
for i in range(k):
p1 = p1.next
p2 = head
# p1 和 p2 同时走 n - k 步
while p1 != None:
p2 = p2.next
p1 = p1.next
# p2 现在指向第 n - k + 1 个节点,即倒数第 k 个节点
return p2// 返回链表的倒数第 k 个节点
func findFromEnd(head *ListNode, k int) *ListNode {
p1 := head
// p1 先走 k 步
for i := 0; i < k; i++ {
p1 = p1.Next
}
p2 := head
// p1 和 p2 同时走 n - k 步
for p1 != nil {
p1 = p1.Next
p2 = p2.Next
}
// p2 现在指向第 n - k + 1 个节点,即倒数第 k 个节点
return p2
}// 返回链表的倒数第 k 个节点
var findFromEnd = function(head, k) {
var p1 = head;
// p1 先走 k 步
for (var i = 0; i < k; i++) {
p1 = p1.next;
}
var p2 = head;
// p1 和 p2 同时走 n - k 步
while (p1 != null) {
p2 = p2.next;
p1 = p1.next;
}
// p2 现在指向第 n - k + 1 个节点,即倒数第 k 个节点
return p2;
};你可以点开下面的可视化面板,代码将计算倒数第二个节点。多次点击 i++ 即可看到快指针 p1 先前进了 2 步,然后多次点击 while (p1 !== null) 这一行代码,即可看到 p1 和 p2 同时前进,最终 p2 停在了倒数第 k 个节点上:
算法可视化面板
当然,如果用 big O 表示法来计算时间复杂度,无论遍历一次链表和遍历两次链表的时间复杂度都是 ,但上述这个算法更有技巧性。
很多链表相关的算法题都会用到这个技巧,比如说力扣第 19 题「删除链表的倒数第 N 个结点」:
19. 删除链表的倒数第 N 个结点 | 力扣 | LeetCode | 🟠
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
示例 1:
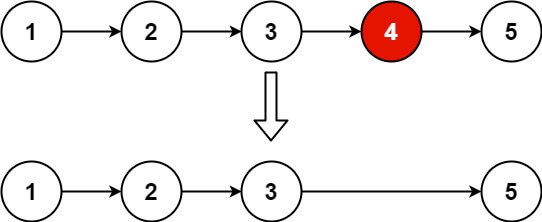
输入:head = [1,2,3,4,5], n = 2 输出:[1,2,3,5]
示例 2:
输入:head = [1], n = 1 输出:[]
示例 3:
输入:head = [1,2], n = 1 输出:[1]
提示:
- 链表中结点的数目为
sz 1 <= sz <= 300 <= Node.val <= 1001 <= n <= sz
进阶:你能尝试使用一趟扫描实现吗?
我们直接看解法代码:
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
// 虚拟头结点
ListNode dummy = new ListNode(-1);
dummy.next = head;
// 删除倒数第 n 个,要先找倒数第 n + 1 个节点
ListNode x = findFromEnd(dummy, n + 1);
// 删掉倒数第 n 个节点
x.next = x.next.next;
return dummy.next;
}
private ListNode findFromEnd(ListNode head, int k) {
// 代码见上文
}
}class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
// 虚拟头结点
ListNode* dummy = new ListNode(-1);
dummy->next = head;
// 删除倒数第 n 个,要先找倒数第 n + 1 个节点
ListNode* x = findFromEnd(dummy, n + 1);
// 删掉倒数第 n 个节点
x->next = x->next->next;
return dummy->next;
}
private:
ListNode* findFromEnd(ListNode* head, int k) {
// 代码见上文
}
};# 主函数
class Solution:
def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
# 虚拟头结点
dummy = ListNode(-1)
dummy.next = head
# 删除倒数第 n 个,要先找倒数第 n + 1 个节点
x = self.findFromEnd(dummy, n + 1)
# 删掉倒数第 n 个节点
x.next = x.next.next
return dummy.next
def findFromEnd(self, head: ListNode, k: int) -> ListNode:
# 代码见上文
passfunc removeNthFromEnd(head *ListNode, n int) *ListNode {
// 虚拟头结点
dummy := &ListNode{Val: -1}
dummy.Next = head
// 删除倒数第 n 个,要先找倒数第 n + 1 个节点
x := findFromEnd(dummy, n+1)
// 删掉倒数第 n 个节点
x.Next = x.Next.Next
return dummy.Next
}
func findFromEnd(head *ListNode, k int) *ListNode {
// 代码见上文
}// 主函数
var removeNthFromEnd = function(head, n) {
// 虚拟头结点
let dummy = new ListNode(-1);
dummy.next = head;
// 删除倒数第 n 个,要先找倒数第 n + 1 个节点
let x = findFromEnd(dummy, n + 1);
// 删掉倒数第 n 个节点
x.next = x.next.next;
return dummy.next;
};
var findFromEnd = function(head, k) {
// 代码见上文
};你可以打开可视化面板,点击 let p2 = head; 这一行代码一次,可以看到 p2 先前进了 k 步,然后多次点击 while (p1 !== null) 这一行代码,可以看到 p1 和 p2 同时前进,最终 p2 停在了倒数第 k 个节点上:
算法可视化面板
这个逻辑就很简单了,要删除倒数第 n 个节点,就得获得倒数第 n + 1 个节点的引用,可以用我们实现的 findFromEnd 来操作。
不过注意我们又使用了虚拟头结点的技巧,也是为了防止出现空指针的情况,比如说链表总共有 5 个节点,题目就让你删除倒数第 5 个节点,也就是第一个节点,那按照算法逻辑,应该首先找到倒数第 6 个节点。但第一个节点前面已经没有节点了,这就会出错。
但有了我们虚拟节点 dummy 的存在,就避免了这个问题,能够对这种情况进行正确的删除。
单链表的中点
力扣第 876 题「链表的中间结点」就是这个题目,问题的关键也在于我们无法直接得到单链表的长度 n,常规方法也是先遍历链表计算 n,再遍历一次得到第 n / 2 个节点,也就是中间节点。
如果想一次遍历就得到中间节点,也需要耍点小聪明,使用「快慢指针」的技巧:
我们让两个指针 slow 和 fast 分别指向链表头结点 head。
每当慢指针 slow 前进一步,快指针 fast 就前进两步,这样,当 fast 走到链表末尾时,slow 就指向了链表中点。
上述思路的代码实现如下:
class Solution {
public ListNode middleNode(ListNode head) {
// 快慢指针初始化指向 head
ListNode slow = head, fast = head;
// 快指针走到末尾时停止
while (fast != null && fast.next != null) {
// 慢指针走一步,快指针走两步
slow = slow.next;
fast = fast.next.next;
}
// 慢指针指向中点
return slow;
}
}class Solution {
public:
ListNode* middleNode(ListNode* head) {
// 快慢指针初始化指向 head
ListNode* slow = head;
ListNode* fast = head;
// 快指针走到末尾时停止
while (fast != nullptr && fast->next != nullptr) {
// 慢指针走一步,快指针走两步
slow = slow->next;
fast = fast->next->next;
}
// 慢指针指向中点
return slow;
}
};class Solution:
# 快慢指针初始化指向 head
def middleNode(self, head: ListNode) -> ListNode:
slow = head
fast = head
# 快指针走到末尾时停止
while fast is not None and fast.next is not None:
# 慢指针走一步,快指针走两步
slow = slow.next
fast = fast.next.next
# 慢指针指向中点
return slowfunc middleNode(head *ListNode) *ListNode {
// 快慢指针初始化指向 head
slow, fast := head, head
// 快指针走到末尾时停止
for fast != nil && fast.Next != nil {
// 慢指针走一步,快指针走两步
slow = slow.Next
fast = fast.Next.Next
}
// 慢指针指向中点
return slow
}var middleNode = function(head) {
// 快慢指针初始化指向 head
let slow = head, fast = head;
// 快指针走到末尾时停止
while (fast !== null && fast.next !== null) {
// 慢指针走一步,快指针走两步
slow = slow.next;
fast = fast.next.next;
}
// 慢指针指向中点
return slow;
};你可以点开可视化面板,点击 while (fast !== null && fast.next !== null) 这一行代码,可以看到快慢指针的运动过程:
算法可视化面板
需要注意的是,如果链表长度为偶数,也就是说中点有两个的时候,我们这个解法返回的节点是靠后的那个节点。
另外,这段代码稍加修改就可以直接用到判断链表成环的算法题上。
判断链表是否包含环
判断链表是否包含环属于经典问题了,解决方案也是用快慢指针:
每当慢指针 slow 前进一步,快指针 fast 就前进两步。
如果 fast 最终能正常走到链表末尾,说明链表中没有环;如果 fast 走着走着竟然和 slow 相遇了,那肯定是 fast 在链表中转圈了,说明链表中含有环。
只需要把寻找链表中点的代码稍加修改就行了:
public class Solution {
public boolean hasCycle(ListNode head) {
// 快慢指针初始化指向 head
ListNode slow = head, fast = head;
// 快指针走到末尾时停止
while (fast != null && fast.next != null) {
// 慢指针走一步,快指针走两步
slow = slow.next;
fast = fast.next.next;
// 快慢指针相遇,说明含有环
if (slow == fast) {
return true;
}
}
// 不包含环
return false;
}
}class Solution {
public:
bool hasCycle(ListNode *head) {
// 快慢指针初始化指向 head
ListNode *slow = head, *fast = head;
// 快指针走到末尾时停止
while (fast != nullptr && fast->next != nullptr) {
// 慢指针走一步,快指针走两步
slow = slow->next;
fast = fast->next->next;
// 快慢指针相遇,说明含有环
if (slow == fast) {
return true;
}
}
// 不包含环
return false;
}
};class Solution:
# 快慢指针初始化指向 head
def hasCycle(self, head: ListNode) -> bool:
slow = head
fast = head
# 快指针走到末尾时停止
while fast is not None and fast.next is not None:
# 慢指针走一步,快指针走两步
slow = slow.next
fast = fast.next.next
# 快慢指针相遇,说明含有环
if slow == fast:
return True
# 不包含环
return Falsefunc hasCycle(head *ListNode) bool {
// 快慢指针初始化指向 head
slow, fast := head, head
// 快指针走到末尾时停止
for fast != nil && fast.Next != nil {
// 慢指针走一步,快指针走两步
slow = slow.Next
fast = fast.Next.Next
// 快慢指针相遇,说明含有环
if slow == fast {
return true
}
}
// 不包含环
return false
}var hasCycle = function(head) {
// 快慢指针初始化指向 head
let slow = head, fast = head;
// 快指针走到末尾时停止
while (fast !== null && fast.next !== null) {
// 慢指针走一步,快指针走两步
slow = slow.next;
fast = fast.next.next;
// 快慢指针相遇,说明含有环
if (slow === fast) {
return true;
}
}
// 不包含环
return false;
};你可以打开下面的可视化面板,多次点击 fast = fast.next.next; 这一行代码,即可看到快慢指针运动的过程,最终相遇:
算法可视化面板
当然,这个问题还有进阶版,也是力扣第 142 题「环形链表 II」:如果链表中含有环,如何计算这个环的起点?
举个例子,环的起点是指下面这幅图中的节点 2:
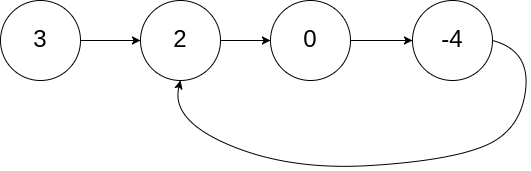
这里先直接看一下寻找环起点的解法代码:
class Solution {
public ListNode detectCycle(ListNode head) {
ListNode fast, slow;
fast = slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) break;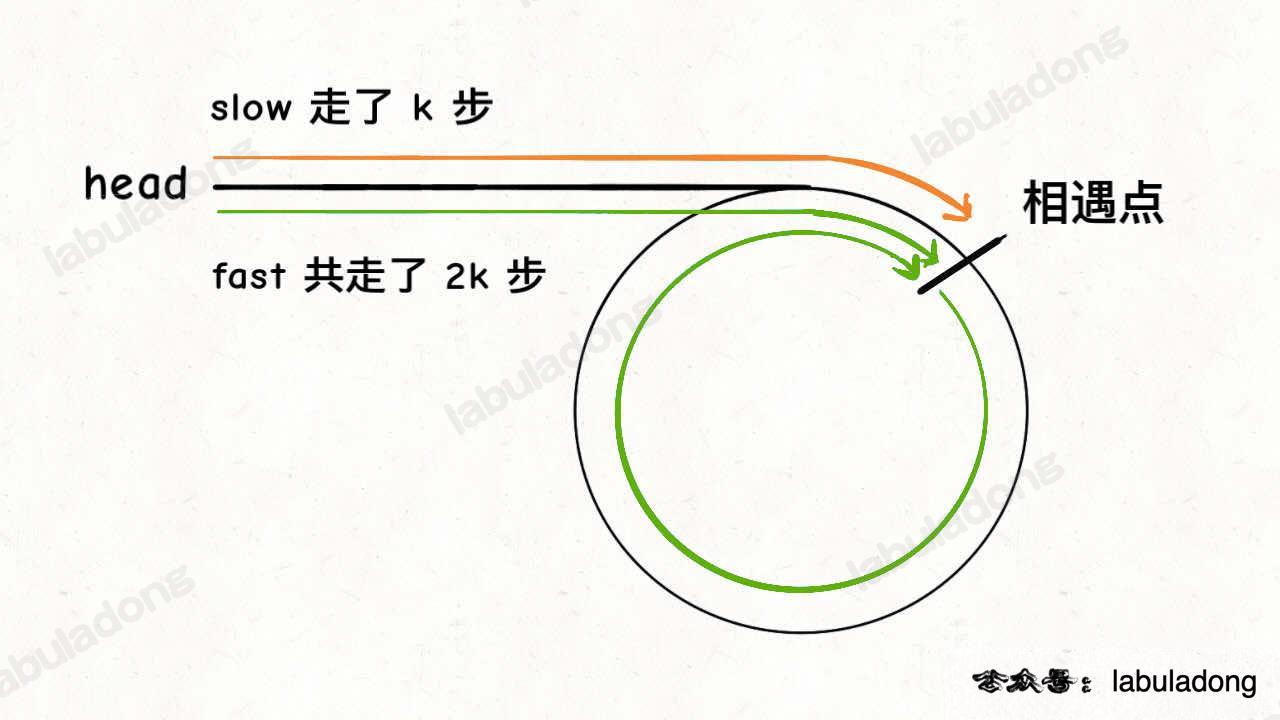 }
// 上面的代码类似 hasCycle 函数
if (fast == null || fast.next == null) {
// fast 遇到空指针说明没有环
return null;
}
// 重新指向头结点
slow = head;
}
// 上面的代码类似 hasCycle 函数
if (fast == null || fast.next == null) {
// fast 遇到空指针说明没有环
return null;
}
// 重新指向头结点
slow = head;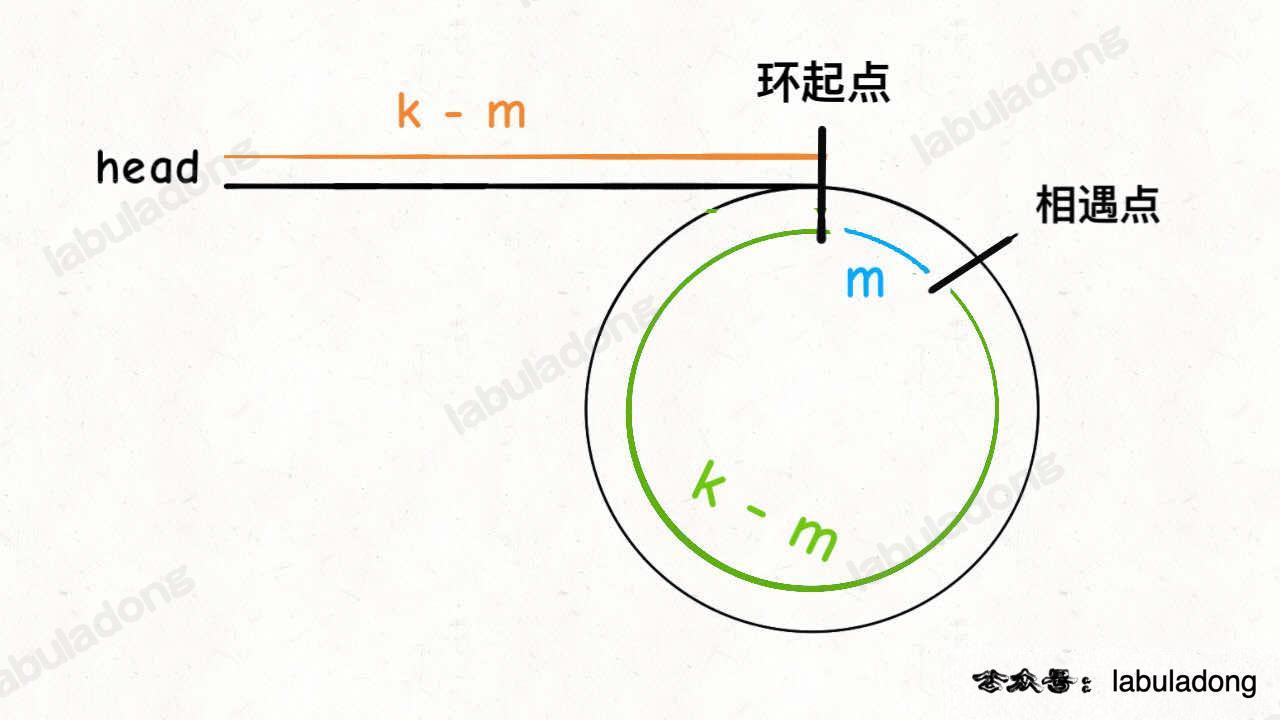 // 快慢指针同步前进,相交点就是环起点
while (slow != fast) {
fast = fast.next;
slow = slow.next;
}
return slow;
}
}
// 快慢指针同步前进,相交点就是环起点
while (slow != fast) {
fast = fast.next;
slow = slow.next;
}
return slow;
}
}class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode *fast, *slow;
fast = slow = head;
while (fast != nullptr && fast->next != nullptr) {
fast = fast->next->next;
slow = slow->next;
if (fast == slow) break; }
// 上面的代码类似 hasCycle 函数
if (fast == nullptr || fast->next == nullptr) {
// fast 遇到空指针说明没有环
return nullptr;
}
// 重新指向头结点
slow = head;
}
// 上面的代码类似 hasCycle 函数
if (fast == nullptr || fast->next == nullptr) {
// fast 遇到空指针说明没有环
return nullptr;
}
// 重新指向头结点
slow = head; // 快慢指针同步前进,相交点就是环起点
while (slow != fast) {
fast = fast->next;
slow = slow->next;
}
return slow;
}
};
// 快慢指针同步前进,相交点就是环起点
while (slow != fast) {
fast = fast->next;
slow = slow->next;
}
return slow;
}
};class Solution:
def detectCycle(self, head: ListNode):
fast, slow = head, head
while fast and fast.next:
fast = fast.next.next
slow = slow.next
if fast == slow:
break # 上面的代码类似 hasCycle 函数
if not fast or not fast.next:
# fast 遇到空指针说明没有环
return None
# 重新指向头结点
slow = head
# 上面的代码类似 hasCycle 函数
if not fast or not fast.next:
# fast 遇到空指针说明没有环
return None
# 重新指向头结点
slow = head  # 快慢指针同步前进,相交点就是环起点
while slow != fast:
fast = fast.next
slow = slow.next
return slow
# 快慢指针同步前进,相交点就是环起点
while slow != fast:
fast = fast.next
slow = slow.next
return slowfunc detectCycle(head *ListNode) *ListNode {
fast, slow := head, head
for fast != nil && fast.Next != nil {
fast = fast.Next.Next
slow = slow.Next
if fast == slow {
break }
}
// 上面的代码类似 hasCycle 函数
if fast == nil || fast.Next == nil {
// fast 遇到空指针说明没有环
return nil
}
// 重新指向头结点
slow = head
}
}
// 上面的代码类似 hasCycle 函数
if fast == nil || fast.Next == nil {
// fast 遇到空指针说明没有环
return nil
}
// 重新指向头结点
slow = head // 快慢指针同步前进,相交点就是环起点
for slow != fast {
fast = fast.Next
slow = slow.Next
}
return slow
}
// 快慢指针同步前进,相交点就是环起点
for slow != fast {
fast = fast.Next
slow = slow.Next
}
return slow
}var detectCycle = function(head) {
let fast, slow;
fast = slow = head;
while (fast !== null && fast.next !== null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) break; }
// 上面的代码类似 hasCycle 函数
if (fast === null || fast.next === null) {
// fast 遇到空指针说明没有环
return null;
}
// 重新指向头结点
slow = head;
}
// 上面的代码类似 hasCycle 函数
if (fast === null || fast.next === null) {
// fast 遇到空指针说明没有环
return null;
}
// 重新指向头结点
slow = head; // 快慢指针同步前进,相交点就是环起点
while (slow !== fast) {
fast = fast.next;
slow = slow.next;
}
return slow;
};
// 快慢指针同步前进,相交点就是环起点
while (slow !== fast) {
fast = fast.next;
slow = slow.next;
}
return slow;
};你可以打开下面的可视化面板,多次点击 fast = fast.next.next; 这一行代码,即可看到快慢指针追逐相遇的过程;然后多次点击 while (slow != fast) 这一行代码,可以看到快慢指针同步前进,最终相遇在环的起点:
算法可视化面板
可以看到,当快慢指针相遇时,让其中任一个指针指向头节点,然后让它俩以相同速度前进,再次相遇时所在的节点位置就是环开始的位置。
为什么要这样呢?这里简单说一下其中的原理。
我们假设快慢指针相遇时,慢指针 slow 走了 k 步,那么快指针 fast 一定走了 2k 步:

fast 一定比 slow 多走了 k 步,这多走的 k 步其实就是 fast 指针在环里转圈圈,所以 k 的值就是环长度的「整数倍」。
假设相遇点距环的起点的距离为 m,那么结合上图的 slow 指针,环的起点距头结点 head 的距离为 k - m,也就是说如果从 head 前进 k - m 步就能到达环起点。
巧的是,如果从相遇点继续前进 k - m 步,也恰好到达环起点。因为结合上图的 fast 指针,从相遇点开始走k步可以转回到相遇点,那走 k - m 步肯定就走到环起点了:

所以,只要我们把快慢指针中的任一个重新指向 head,然后两个指针同速前进,k - m 步后一定会相遇,相遇之处就是环的起点了。
两个链表是否相交
这个问题有意思,也是力扣第 160 题「相交链表」函数签名如下:
ListNode getIntersectionNode(ListNode headA, ListNode headB);ListNode* getIntersectionNode(ListNode* headA, ListNode* headB);def getIntersectionNode(headA: ListNode, headB: ListNode) -> ListNode:func getIntersectionNode(headA *ListNode, headB *ListNode) *ListNodevar getIntersectionNode = function(headA, headB)给你输入两个链表的头结点 headA 和 headB,这两个链表可能存在相交。
如果相交,你的算法应该返回相交的那个节点;如果没相交,则返回 null。
比如题目给我们举的例子,如果输入的两个链表如下图:
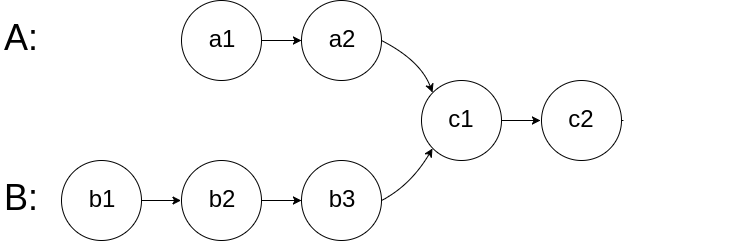
那么我们的算法应该返回 c1 这个节点。
这个题直接的想法可能是用 HashSet 记录一个链表的所有节点,然后和另一条链表对比,但这就需要额外的空间。
如果不用额外的空间,只使用两个指针,你如何做呢?
难点在于,由于两条链表的长度可能不同,两条链表之间的节点无法对应:
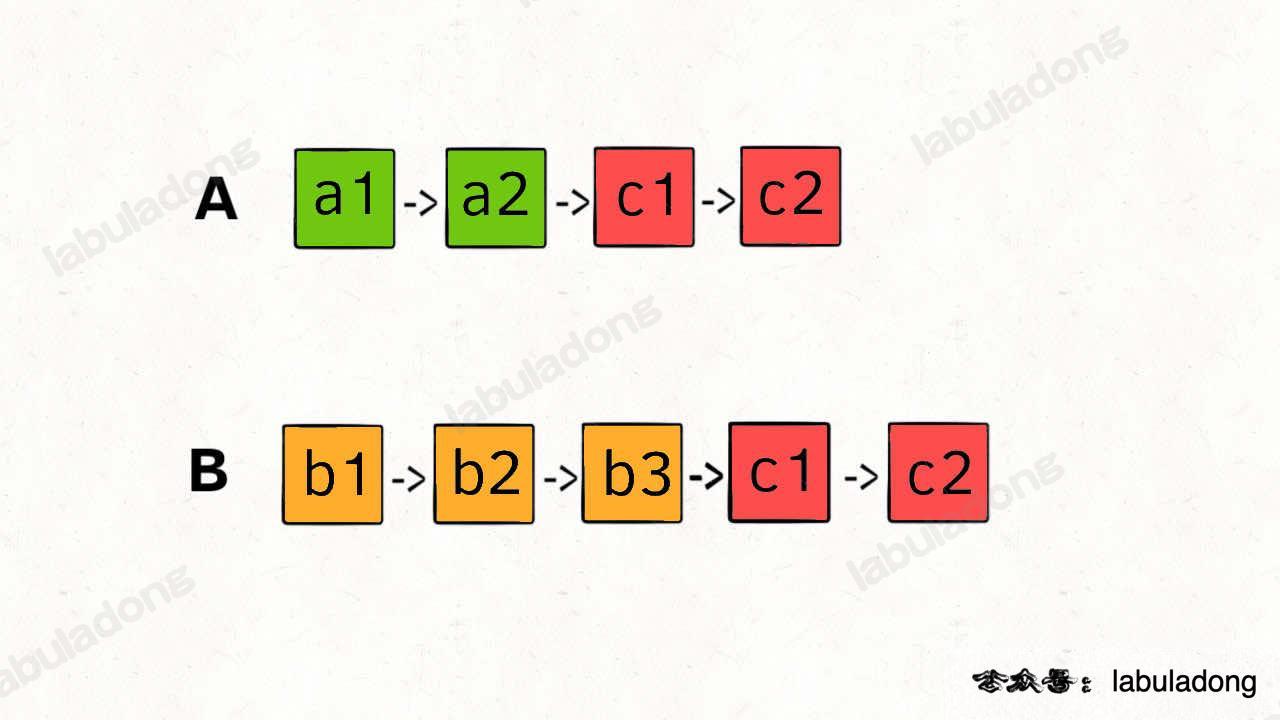
如果用两个指针 p1 和 p2 分别在两条链表上前进,并不能同时走到公共节点,也就无法得到相交节点 c1。
解决这个问题的关键是,通过某些方式,让 p1 和 p2 能够同时到达相交节点 c1。
所以,我们可以让 p1 遍历完链表 A 之后开始遍历链表 B,让 p2 遍历完链表 B 之后开始遍历链表 A,这样相当于「逻辑上」两条链表接在了一起。
如果这样进行拼接,就可以让 p1 和 p2 同时进入公共部分,也就是同时到达相交节点 c1:
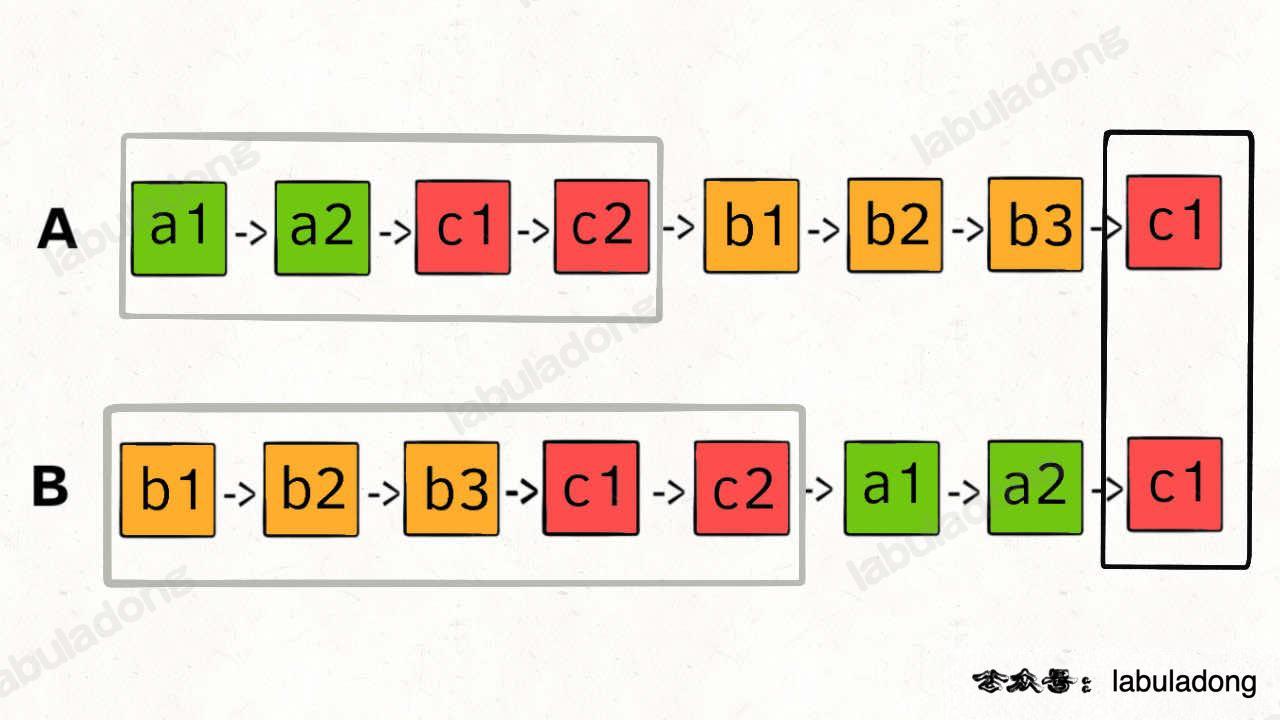
那你可能会问,如果说两个链表没有相交点,是否能够正确的返回 null 呢?
这个逻辑可以覆盖这种情况的,相当于 c1 节点是 null 空指针嘛,可以正确返回 null。
按照这个思路,可以写出如下代码:
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
// p1 指向 A 链表头结点,p2 指向 B 链表头结点
ListNode p1 = headA, p2 = headB;
while (p1 != p2) {
// p1 走一步,如果走到 A 链表末尾,转到 B 链表
if (p1 == null) p1 = headB;
else p1 = p1.next;
// p2 走一步,如果走到 B 链表末尾,转到 A 链表
if (p2 == null) p2 = headA;
else p2 = p2.next;
}
return p1;
}
}class Solution {
public:
ListNode* getIntersectionNode(ListNode* headA, ListNode* headB) {
// p1 指向 A 链表头结点,p2 指向 B 链表头结点
ListNode* p1 = headA;
ListNode* p2 = headB;
while (p1 != p2) {
// p1 走一步,如果走到 A 链表末尾,转到 B 链表
p1 = (p1 == nullptr) ? headB : p1->next;
// p2 走一步,如果走到 B 链表末尾,转到 A 链表
p2 = (p2 == nullptr) ? headA : p2->next;
}
return p1;
}
};class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
# p1 指向 A 链表头结点,p2 指向 B 链表头结点
p1, p2 = headA, headB
while p1 != p2:
# p1 走一步,如果走到 A 链表末尾,转到 B 链表
p1 = headB if p1 is None else p1.next
# p2 走一步,如果走到 B 链表末尾,转到 A 链表
p2 = headA if p2 is None else p2.next
return p1func getIntersectionNode(headA, headB *ListNode) *ListNode {
// p1 指向 A 链表头结点,p2 指向 B 链表头结点
p1, p2 := headA, headB
for p1 != p2 {
// p1 走一步,如果走到 A 链表末尾,转到 B 链表
if p1 == nil {
p1 = headB
} else {
p1 = p1.Next
}
// p2 走一步,如果走到 B 链表末尾,转到 A 链表
if p2 == nil {
p2 = headA
} else {
p2 = p2.Next
}
}
return p1
}var getIntersectionNode = function(headA, headB) {
// p1 指向 A 链表头结点,p2 指向 B 链表头结点
let p1 = headA, p2 = headB;
while (p1 !== p2) {
// p1 走一步,如果走到 A 链表末尾,转到 B 链表
if (p1 === null) p1 = headB;
else p1 = p1.next;
// p2 走一步,如果走到 B 链表末尾,转到 A 链表
if (p2 === null) p2 = headA;
else p2 = p2.next;
}
return p1;
};你可以打开下面的可视化面板,多次点击 while (p1 !== p2) 这一行代码,即可看到两个指针在交点相遇的过程:
算法可视化面板
这样,这道题就解决了,空间复杂度为 ,时间复杂度为 。
以上就是单链表的所有技巧,希望对你有启发。
2022/1/24 更新:
评论区有不少优秀读者对最后一题「寻找两条链表的交点」提出了一些其他思路,也补充到这里。
首先有读者提到,如果把两条链表首尾相连,那么「寻找两条链表的交点」的问题转换成了前面讲的「寻找环起点」的问题:
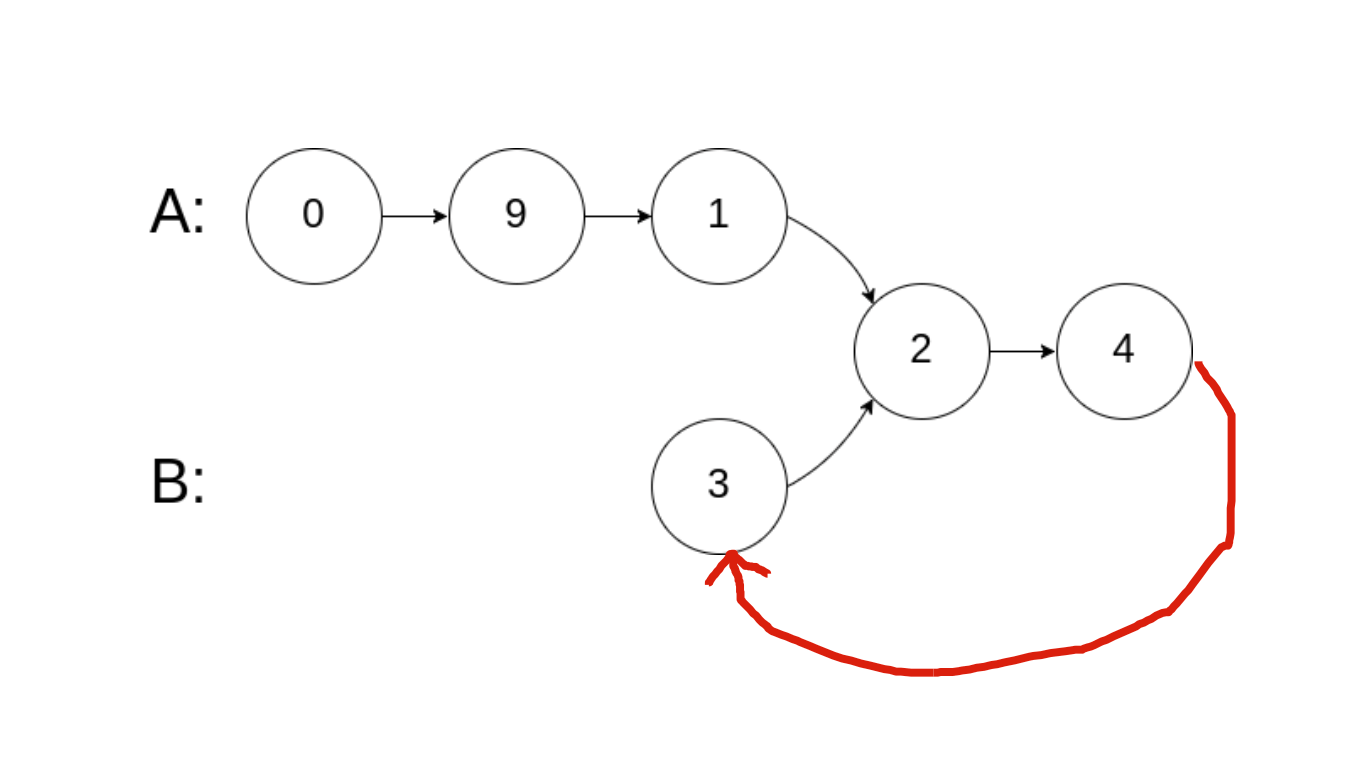
说实话我没有想到这种思路,不得不说这是一个很巧妙的转换!不过需要注意的是,这道题说不让你改变原始链表的结构,所以你把题目输入的链表转化成环形链表求解之后记得还要改回来,否则无法通过。
另外,还有读者提到,既然「寻找两条链表的交点」的核心在于让 p1 和 p2 两个指针能够同时到达相交节点 c1,那么可以通过预先计算两条链表的长度来做到这一点,具体代码如下:
class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
int lenA = 0, lenB = 0;
// 计算两条链表的长度
for (ListNode p1 = headA; p1 != null; p1 = p1.next) {
lenA++;
}
for (ListNode p2 = headB; p2 != null; p2 = p2.next) {
lenB++;
}
// 让 p1 和 p2 到达尾部的距离相同
ListNode p1 = headA, p2 = headB;
if (lenA > lenB) {
for (int i = 0; i < lenA - lenB; i++) {
p1 = p1.next;
}
} else {
for (int i = 0; i < lenB - lenA; i++) {
p2 = p2.next;
}
}
// 看两个指针是否会相同,p1 == p2 时有两种情况:
// 1、要么是两条链表不相交,他俩同时走到尾部空指针
// 2、要么是两条链表相交,他俩走到两条链表的相交点
while (p1 != p2) {
p1 = p1.next;
p2 = p2.next;
}
return p1;
}
}class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
int lenA = 0, lenB = 0;
// 计算两条链表的长度
for (ListNode* p1 = headA; p1 != nullptr; p1 = p1->next) {
lenA++;
}
for (ListNode* p2 = headB; p2 != nullptr; p2 = p2->next) {
lenB++;
}
// 让 p1 和 p2 到达尾部的距离相同
ListNode* p1 = headA;
ListNode* p2 = headB;
if (lenA > lenB) {
for (int i = 0; i < lenA - lenB; i++) {
p1 = p1->next;
}
} else {
for (int i = 0; i < lenB - lenA; i++) {
p2 = p2->next;
}
}
// 看两个指针是否会相同,p1 == p2 时有两种情况:
// 1、要么是两条链表不相交,他俩同时走到尾部空指针
// 2、要么是两条链表相交,他俩走到两条链表的相交点
while (p1 != p2) {
p1 = p1->next;
p2 = p2->next;
}
return p1;
}
};class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
lenA, lenB = 0, 0
# 计算两条链表的长度
p1, p2 = headA, headB
while p1:
lenA += 1
p1 = p1.next
while p2:
lenB += 1
p2 = p2.next
# 让 p1 和 p2 到达尾部的距离相同
p1, p2 = headA, headB
if lenA > lenB:
for _ in range(lenA - lenB):
p1 = p1.next
else:
for _ in range(lenB - lenA):
p2 = p2.next
# 看两个指针是否会相同,p1 == p2 时有两种情况:
# 1、要么是两条链表不相交,他俩同时走到尾部空指针
# 2、要么是两条链表相交,他俩走到两条链表的相交点
while p1 != p2:
p1 = p1.next
p2 = p2.next
return p1func getIntersectionNode(headA, headB *ListNode) *ListNode {
lenA, lenB := 0, 0
// 计算两条链表的长度
for p1 := headA; p1 != nil; p1 = p1.Next {
lenA++
}
for p2 := headB; p2 != nil; p2 = p2.Next {
lenB++
}
// 让 p1 和 p2 到达尾部的距离相同
p1, p2 := headA, headB
if lenA > lenB {
for i := 0; i < lenA - lenB; i++ {
p1 = p1.Next
}
} else {
for i := 0; i < lenB - lenA; i++ {
p2 = p2.Next
}
}
// 看两个指针是否会相同,p1 == p2 时有两种情况:
// 1、要么是两条链表不相交,他俩同时走到尾部空指针
// 2、要么是两条链表相交,他俩走到两条链表的相交点
for p1 != p2 {
p1 = p1.Next
p2 = p2.Next
}
return p1
}var getIntersectionNode = function(headA, headB) {
let lenA = 0, lenB = 0;
// 计算两条链表的长度
for (let p1 = headA; p1 != null; p1 = p1.next) {
lenA++;
}
for (let p2 = headB; p2 != null; p2 = p2.next) {
lenB++;
}
// 让 p1 和 p2 到达尾部的距离相同
let p1 = headA, p2 = headB;
if (lenA > lenB) {
for (let i = 0; i < lenA - lenB; i++) {
p1 = p1.next;
}
} else {
for (let i = 0; i < lenB - lenA; i++) {
p2 = p2.next;
}
}
// 看两个指针是否会相同,p1 == p2 时有两种情况:
// 1、要么是两条链表不相交,他俩同时走到尾部空指针
// 2、要么是两条链表相交,他俩走到两条链表的相交点
while (p1 != p2) {
p1 = p1.next;
p2 = p2.next;
}
return p1;
};虽然代码多一些,但是时间复杂度是还是 ,而且会更容易理解一些。
总之,我的解法代码并不一定就是最优或者最正确的,鼓励大家在评论区多多提出自己的疑问和思考,我也很高兴和大家探讨更多的解题思路~
到这里,链表相关的双指针技巧就全部讲完了,这些技巧的更多扩展延伸见 更多链表双指针经典习题。