Ball and Box: Two Perspectives of Backtracking Enumeration

Before diving into this article, you need to be familiar with the Backtracking Algorithm Core Framework and Backtracking Algorithm to Solve All Permutations/Combinations/Subsets.

In these two articles, readers have suggested different ways to write permutation/combination/subset code, such as using swap to achieve full permutations and subset solutions without for loops. I previously avoided discussing these alternative methods to maintain consistency in problem-solving approaches. Introducing too many options early on can be confusing.

In this article, I will not only introduce the backtracking algorithm methods I haven't covered before but also explain why they work and what the essential differences are between the two approaches.

Brute-Force Enumeration Method: The Ball and Box Model

All brute-force enumeration algorithms start with the ball and box model, without exception.

Once you understand this, you can effortlessly apply brute-force enumeration algorithms. Please read the following content carefully and think deeply.

First, let's review some previously learned knowledge about permutations and combinations:

1. P(n, k) (often written as A(n, k) in many texts) represents the total number of permutations (or arrangements) of selecting k elements from n distinct elements; C(n, k) represents the total number of combinations of selecting k elements from n distinct elements.

2. The main difference between "permutation" and "combination" is whether the order of elements is considered.

3. The formulas for calculating the total number of permutations and combinations:

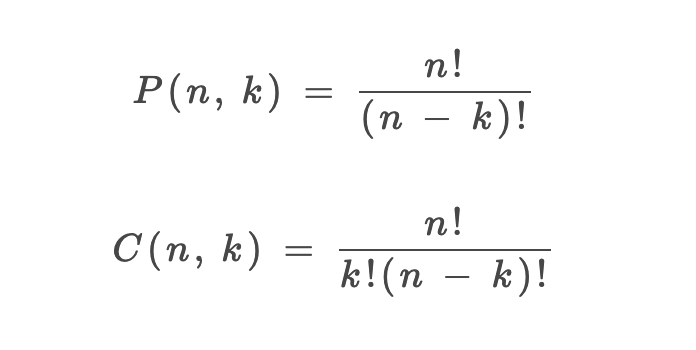
Permutation P(n, k)

Now, let me ask a question: how is the permutation formula P(n, k) derived? To clarify this, I need to discuss some concepts from combinatorial mathematics.

Various variations of permutation and combination problems can be abstracted into the "ball and box model." The permutation P(n, k) can be represented by the following scenario:

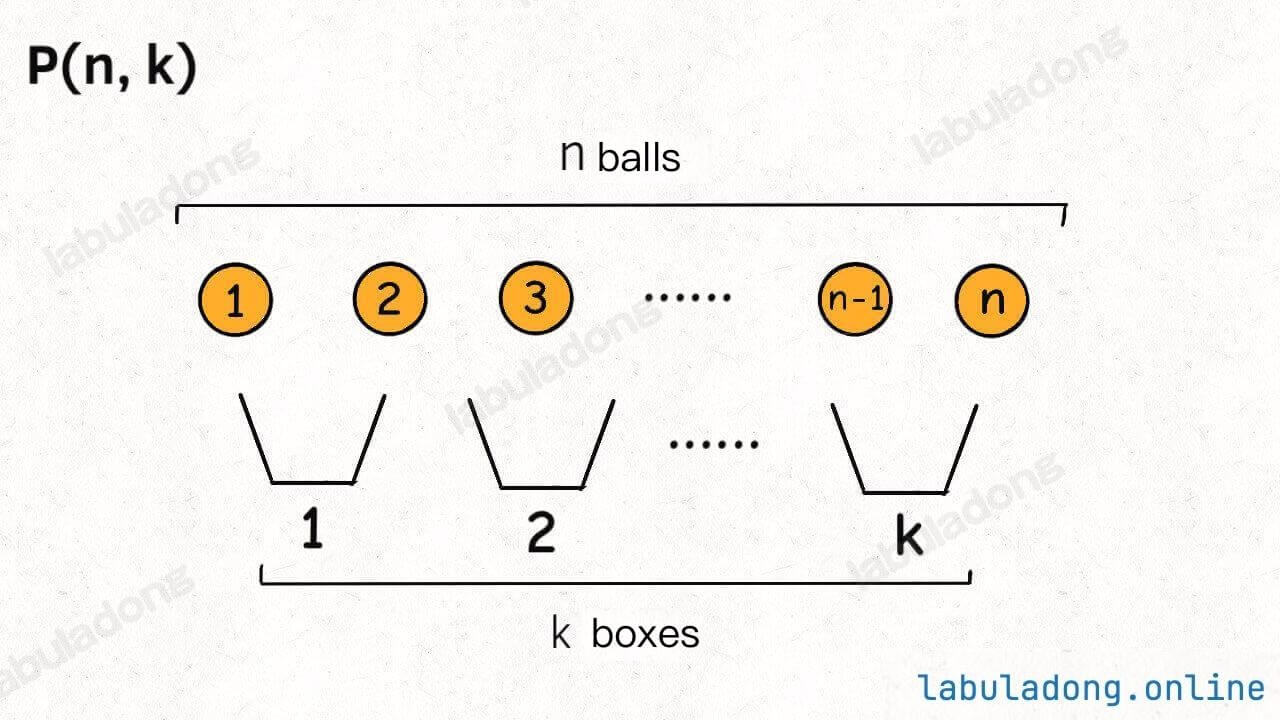
That is, placing n balls, each with a different number to indicate order, into k boxes, each also numbered differently (where n >= k, and each box ends up with exactly one ball). There are P(n, k) different ways to do this.

Now, when you place balls into boxes, how would you do it? There are two perspectives to consider.

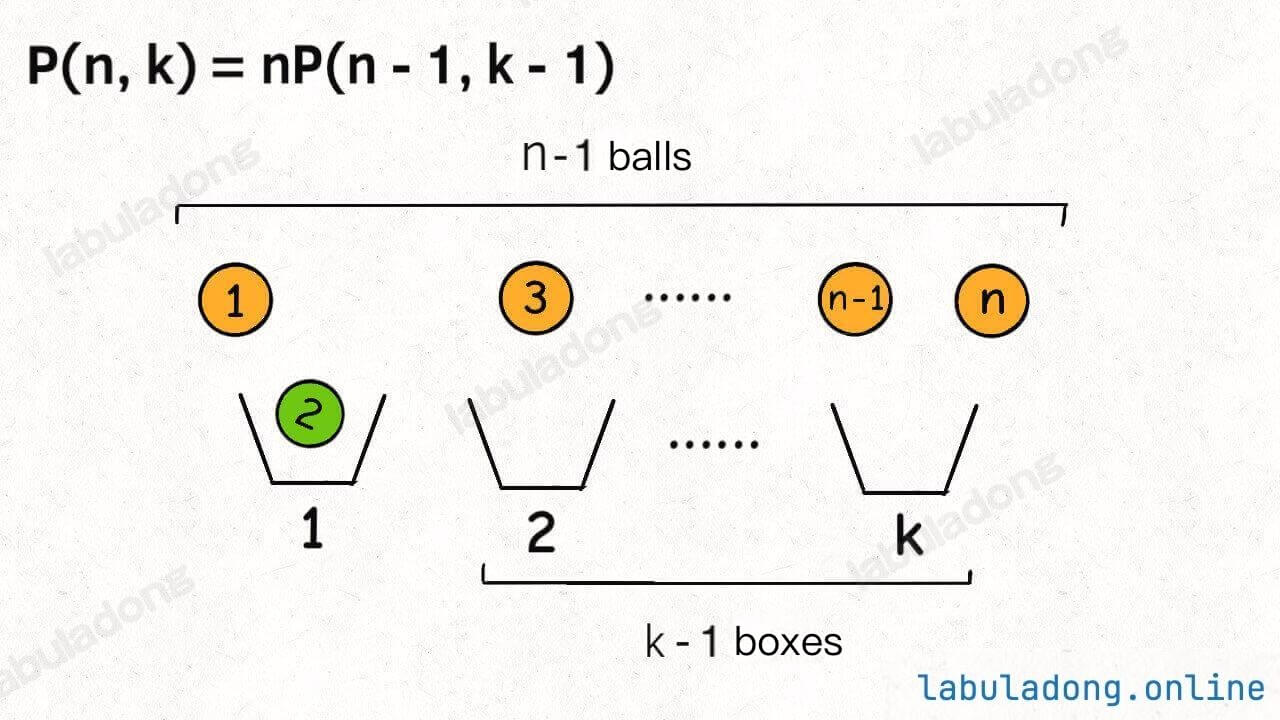
First, from the perspective of the boxes, each box must choose one ball.

In this view, the first box can choose any of the n balls, and then the remaining k - 1 boxes need to choose from the n - 1 balls left (this is the subproblem P(n - 1, k - 1)):

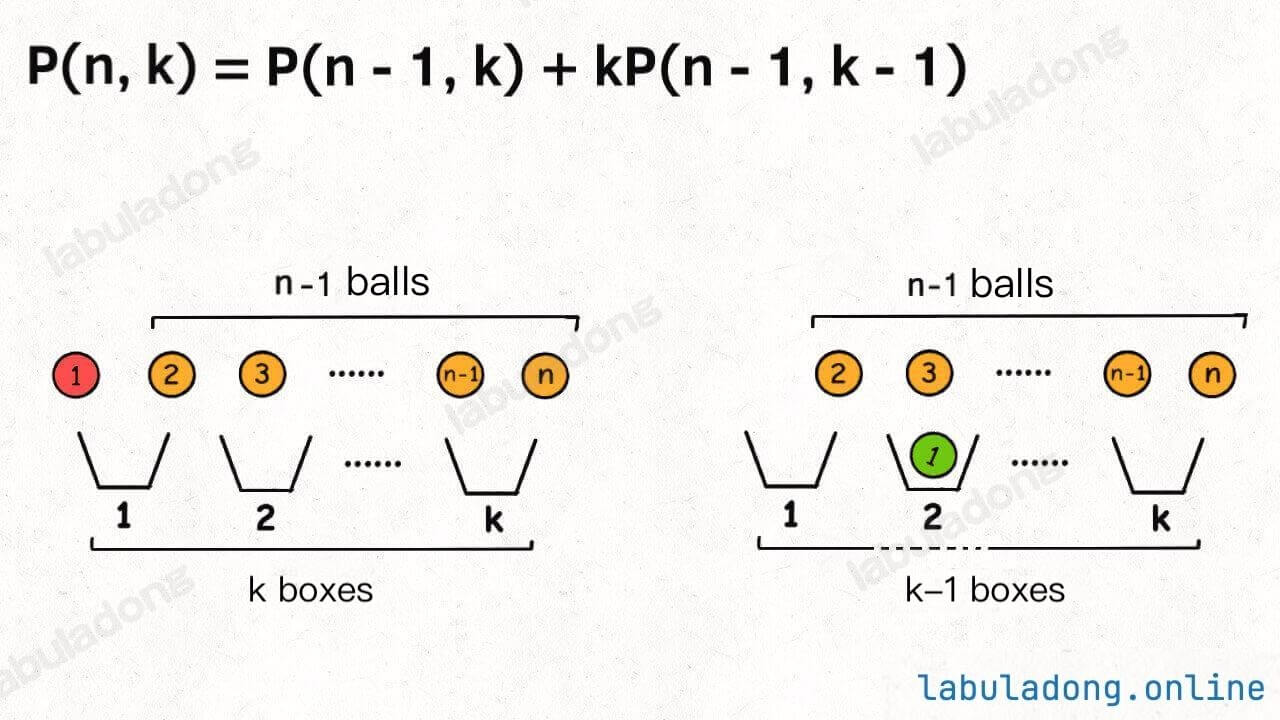
Alternatively, from the perspective of the balls, not every ball will be placed in a box, so there are two situations:

1. The first ball might not be placed in any box, leaving you to place the remaining n - 1 balls into k boxes.

2. The first ball could be placed in any of the k boxes, so you would then place the remaining n - 1 balls into k - 1 boxes.

Combining these two situations, we obtain:

As you can see, the two perspectives yield two different recursive formulas, but both lead to the factorial form we are familiar with:

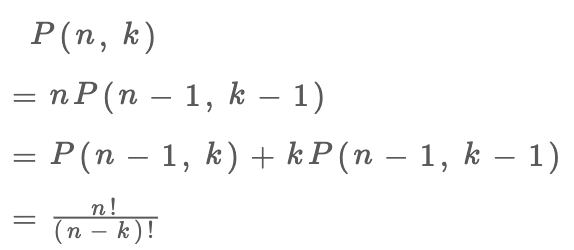
The process of solving these recursive formulas involves more mathematical content, which we will not delve into here. Interested readers are encouraged to study combinatorial mathematics on their own.

Combination C(n, k)

After understanding the derivation process of permutations, the derivation of combinations is similar. It involves making choices from the perspectives of balls and boxes, and can also be expressed in two equivalent forms. Pause here for a few minutes to see if you can come up with a derivation process for combinations on your own.

Now, let me guide you through the derivation. The combination C(n, k) can be abstracted into the following scenario:

In the problem of combinations, we do not care about the order of elements, meaning {1, 2, 3} and {1, 3, 2} are considered the same combination. Therefore, we do not need to number the boxes; we can assume there is only one box with a capacity of k.

Now, as you place the balls into the box, how would you proceed? There are still two perspectives.

Firstly, you can take the perspective of the box, which must hold k balls.

The first ball can be any one of the n balls, and then the box has k - 1 remaining slots, requiring you to choose from the remaining n - 1 balls (this is the subproblem C(n - 1, k - 1)).

At this point, you might think to establish the relationship C(n, k) = nC(n - 1, k - 1).

However, there's a pitfall here. Directly using nC(n - 1, k - 1) results in repetitions. The correct answer should be nC(n - 1, k - 1) / k:

Additionally, you can consider the perspective of the ball, as not every ball will be placed into a box. Thus, there are two scenarios from the ball's perspective:

1. The first ball may not be placed into a box. In this case, you need to place the remaining n - 1 balls into k boxes.

2. The first ball can be placed into a box. In this scenario, you need to place the remaining n - 1 balls into k - 1 boxes.

Combining these two cases, we get:

Note the difference between combinations and permutations. Combinations do not consider order, so when a ball is placed into a box, there is only one choice, not k different choices. Therefore, C(n-1, k-1) does not need to be multiplied by k.

As you can see, these two perspectives lead to two different recursive formulas, but both resolve to the familiar combination formula:

As for solving the recursive formula, it involves a lot of mathematics, which we will not delve into here.

In the above content, I guided you through deriving the mathematical formula for permutations and combinations. However, the focus is not on mathematics, but rather, have you gained a deeper understanding of "exhaustive search"?

Reinterpreting the Full Permutation Problem with the Ball-Box Model

Alright, the above section introduced two perspectives on exhaustive permutations from a mathematical viewpoint. Now, let's return to the code, and I will test your understanding.

In previous articles, Core Framework of Backtracking Algorithm and Nine Variants of Permutation/Combination/Subsets with Backtracking Algorithm, we provided code for full permutations.

Let's use the basic example of permutations without repetition and without replacement. I will directly copy the code here:

class Solution {

    List<List<Integer>> res = new LinkedList<>();
    // record the recursive path of backtracking algorithm
    LinkedList<Integer> track = new LinkedList<>();
    // elements in track will be marked as true
    boolean[] used;

    // main function, input a set of non-repeating numbers, return all permutations
    public List<List<Integer>> permute(int[] nums) {
        used = new boolean[nums.length];
        backtrack(nums);
        return res;
    }

    // core function of backtracking algorithm
    void backtrack(int[] nums) {
        // base case, reach the leaf node
        if (track.size() == nums.length) {
            // collect the values at the leaf node
            res.add(new LinkedList(track));
            return;
        }

        // standard framework of backtracking algorithm
        for (int i = 0; i < nums.length; i++) {
            // elements already in track, cannot be selected again
            if (used[i]) {
                continue;
            }
            // make a choice
            used[i] = true;
            track.addLast(nums[i]);
            // enter the next level of backtracking tree
            backtrack(nums);
            // cancel the choice
            track.removeLast();
            used[i] = false;
        }
    }
}

class Solution {
public:
    vector<vector<int>> res;
    // record the recursive path of backtracking algorithm
    vector<int> track;
    // elements in track will be marked as true
    vector<bool> used;

    // main function, input a set of non-repeating numbers, return all permutations
    vector<vector<int>> permute(vector<int>& nums) {
        used = vector<bool>(nums.size(), false);
        backtrack(nums);
        return res;
    }

    // core function of backtracking algorithm
    void backtrack(vector<int>& nums) {
        // base case, reach the leaf node
        if (track.size() == nums.size()) {
            // collect the value at the leaf node
            res.push_back(track);
            return;
        }

        // standard framework of backtracking algorithm
        for (int i = 0; i < nums.size(); i++) {
            // elements already in track cannot be selected again
            if (used[i]) {
                continue;
            }
            // make a choice
            used[i] = true;
            track.push_back(nums[i]);
            // enter the next level of backtracking tree
            backtrack(nums);
            // cancel the choice
            track.pop_back();
            used[i] = false;
        }
    }
};

class Solution:
    def __init__(self):
        self.res = []
        self.track = []
        self.used = []

    # main function, input a set of non-repeating numbers, return all permutations
    def permute(self, nums):
        self.used = [False] * len(nums)
        self.backtrack(nums)
        return self.res

    # backtracking core function
    def backtrack(self, nums):
        # base case, reach the leaf node
        if len(self.track) == len(nums):
            # collect the value at the leaf node
            self.res.append(self.track[:])
            return

        for i in range(len(nums)):
            # elements already in track cannot be selected repeatedly
            if self.used[i]:
                continue
            # make a choice
            self.used[i] = True
            self.track.append(nums[i])
            # go to the next level of backtracking tree
            self.backtrack(nums)
            # cancel the choice
            self.track.pop()
            self.used[i] = False

func permute(nums []int) [][]int {
	res := [][]int{}
	track := []int{}
	used := make([]bool, len(nums))

	// backtracking core function
	var backtrack func(nums []int)
	backtrack = func(nums []int) {
		// base case, reach the leaf node
		if len(track) == len(nums) {
			// collect the values at the leaf node
			temp := make([]int, len(track))
			copy(temp, track)
			res = append(res, temp)
			return
		}

		// standard framework for backtracking
		for i := 0; i < len(nums); i++ {
			// elements already in track, cannot be selected again
			if used[i] {
				continue
			}
			// make a choice
			used[i] = true
			track = append(track, nums[i])
			// go to the next level of the backtracking tree
			backtrack(nums)
			// cancel the choice
			track = track[:len(track)-1]
			used[i] = false
		}
	}

	backtrack(nums)
	return res
}

var permute = function(nums) {
    const res = [];
    // record the recursive path of the backtracking algorithm
    const track = [];
    // elements in track will be marked as true
    const used = new Array(nums.length).fill(false);

    // the core function of the backtracking algorithm
    function backtrack(nums) {
        // base case, reach the leaf node
        if (track.length === nums.length) {
            // collect the value at the leaf node
            res.push([...track]);
            return;
        }

        // the standard framework of the backtracking algorithm
        for (let i = 0; i < nums.length; i++) {
            // elements already in track cannot be selected again
            if (used[i]) {
                continue;
            }
            // make a choice
            used[i] = true;
            track.push(nums[i]);
            // go to the next level of the backtracking tree
            backtrack(nums);
            // cancel the choice
            track.pop();
            used[i] = false;
        }
    }

    backtrack(nums);

    return res;

};

Why is this the answer? Suppose nums contains n numbers. The problem of generating all permutations is equivalent to placing n balls into n boxes, where each box must be filled. The question is, how many different ways can you do this?

From the box's perspective, the first position in the box can receive any of the n balls, giving n choices. The second position can receive any of the n - 1 remaining balls, giving n - 1 choices. The third position has n - 2 choices, and so on.

I directly use the Algorithm Visualization Panel to draw the recursion tree. You can understand it at a glance. Please drag the progress bar to the end to display the entire backtracking tree, then move your mouse horizontally across each level of nodes to observe the values on the nodes and branches of the recursion tree:

First, I list the solution code that uses swap to calculate permutations. Please take a look at it first:

class Solution {

    List<List<Integer>> result = new ArrayList<>();

    public List<List<Integer>> permute(int[] nums) {
        backtrack(nums, 0);
        return result;
    }

    // backtracking algorithm core framework
    void backtrack(int[] nums, int start) {
        if (start == nums.length) {
            // found a permutation, need to convert to List type in Java
            List<Integer> list = new ArrayList<>();
            for (int num : nums) {
                list.add(num);
            }
            result.add(list);
            return;
        }

        for (int i = start; i < nums.length; i++) {
            // make a choice
            swap(nums, start, i);
            // recursive call with start + 1
            backtrack(nums, start + 1);
            // undo the choice
            swap(nums, start, i);
        }
    }

    void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

class Solution {
private:
    vector<vector<int>> result;

public:
    vector<vector<int>> permute(vector<int>& nums) {
        backtrack(nums, 0);
        return result;
    }

    // backtracking algorithm core framework
    void backtrack(vector<int>& nums, int start) {
        if (start == nums.size()) {
            // found a permutation, Java needs to convert to List type
            result.push_back(nums);
            return;
        }

        for (int i = start; i < nums.size(); i++) {
            // make a choice
            swap(nums, start, i);
            // recursive call with start + 1
            backtrack(nums, start + 1);
            // undo the choice
            swap(nums, start, i);
        }
    }

    void swap(vector<int>& nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
};

class Solution:

    def __init__(self):
        self.result = []

    def permute(self, nums):
        self.backtrack(nums, 0)
        return self.result

    # the core framework of backtracking algorithm
    def backtrack(self, nums, start):
        if start == len(nums):
            # found a permutation, Python directly converts it to a List type
            self.result.append(list(nums))
            return

        for i in range(start, len(nums)):
            # make a choice
            self.swap(nums, start, i)
            # recursive call with start + 1
            self.backtrack(nums, start + 1)
            # undo the choice
            self.swap(nums, start, i)

    def swap(self, nums, i, j):
        temp = nums[i]
        nums[i] = nums[j]
        nums[j] = temp

// Function to return all permutations of the problem
func permute(nums []int) [][]int {
    var result [][]int
    backtrack(nums, 0, &result)
    return result
}

// Core framework of backtracking algorithm
func backtrack(nums []int, start int, result *[][]int) {
    if start == len(nums) {
        // Found a permutation, Java needs to convert to List type
        list := append([]int(nil), nums...)
        *result = append(*result, list)
        return
    }

    for i := start; i < len(nums); i++ {
        // Make a choice
        swap(nums, start, i)
        // Recursive call with start + 1
        backtrack(nums, start + 1, result)
        // Undo the choice
        swap(nums, start, i)
    }
}

func swap(nums []int, i int, j int) {
    temp := nums[i]
    nums[i] = nums[j]
    nums[j] = temp
}

var permute = function(nums) {
    const result = [];

    // the core framework of backtracking algorithm
    function backtrack(start) {
        if (start === nums.length) {
            // find a permutation, directly convert to List type in Python
            result.push([...nums]);
            return;
        }

        for (let i = start; i < nums.length; i++) {
            // make a choice
            swap(start, i);
            // recursive call with start + 1
            backtrack(start + 1);
            // undo the choice
            swap(start, i);
        }
    }

    function swap(i, j) {
        [nums[i], nums[j]] = [nums[j], nums[i]];
    }

    backtrack(0);
    return result;
};

This solution can also correctly calculate permutations. Think about it, from which perspective does this code perform exhaustive enumeration? Is it from the perspective of the balls or the boxes?

I can use the Algorithm Visualization Panel to draw the recursive tree, and you can understand it at a glance. Please drag the progress bar to the end to display the entire backtracking tree, then move the mouse horizontally across each level of nodes to observe the values on the recursive tree nodes and branches:

Of course! Writing a permutation solution from the ball's perspective means each element in nums chooses the index it wants to go to, right? With this thought, the code isn't hard to write.

First, I'll use the Algorithm Visualization Panel to draw the recursive tree. Please drag the progress bar to the end to display the entire backtracking tree, then move the mouse horizontally across each level of nodes to observe the values on the recursive tree nodes and branches, and verify if the elements are choosing the indices:

Of course, there is some room for minor optimizations in my code. For example, swapIndex is actually i, and we don't actually need to wait until count == nums.length. We can return when count == nums.length - 1 because the last remaining element will have no other position to go to. I'll leave these optimizations to you.

class Solution {
    // result list
    List<List<Integer>> res;
    // mark if the element has been used
    boolean[] used;
    // record how many elements have chosen their positions
    int count;

    public List<List<Integer>> permute(int[] nums) {
        res = new ArrayList<>();
        used = new boolean[nums.length];
        count = 0;

        backtrack(nums);
        return res;
    }

    // backtracking algorithm framework
    void backtrack(int[] nums) {
        if (count == nums.length) {
            List<Integer> temp = new ArrayList<>();
            for (int num : nums) {
                temp.add(num);
            }
            res.add(temp);
            return;
        }

        // find two positions that have not been chosen
        int originalIndex = -1, swapIndex = -1;

        for (int i = 0; i < nums.length; i++) {
            if (used[i]) {
                continue;
            }
            if (originalIndex == -1) {
                originalIndex = i;
            }
            swapIndex = i;

            // make a choice, element nums[originalIndex] chooses the swapIndex position
            swap(nums, originalIndex, swapIndex);
            used[swapIndex] = true;
            count++;
            // go to the next level of the decision tree
            backtrack(nums);
            // undo the choice, restore it as it was
            count--;
            used[swapIndex] = false;
            swap(nums, originalIndex, swapIndex);
        }
    }

    void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

class Solution {
public:
    // result list
    vector<vector<int>> res;
    // mark whether the element has been used
    vector<bool> used;
    // record how many elements have chosen their positions
    int count;

    vector<vector<int>> permute(vector<int>& nums) {
        count = 0;
        used = vector<bool>(nums.size(), false);

        backtrack(nums);
        return res;
    }

    // backtracking algorithm framework
    void backtrack(vector<int>& nums) {
        if (count == nums.size()) {
            res.push_back(nums);
            return;
        }

        // find two unselected positions
        int originalIndex = -1, swapIndex = -1;

        for (int i = 0; i < nums.size(); i++) {
            if (used[i]) {
                continue;
            }
            if (originalIndex == -1) {
                originalIndex = i;
            }
            swapIndex = i;

            // make a choice, element nums[originalIndex] chooses the swapIndex position
            swap(nums, originalIndex, swapIndex);
            used[swapIndex] = true;
            count++;
            // go to the next level of decision tree
            backtrack(nums);
            // undo the choice, restore it as it was
            count--;
            used[swapIndex] = false;
            swap(nums, originalIndex, swapIndex);
        }
    }

    void swap(vector<int>& nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
};

class Solution:
    def __init__(self):
        # result list
        self.res = []
        # mark whether the element has been used
        self.used = []
        # record how many elements have chosen their positions
        self.count = 0

    def permute(self, nums):
        self.res = []
        self.used = [False] * len(nums)
        self.count = 0

        self.backtrack(nums)
        return self.res

    # backtracking algorithm framework
    def backtrack(self, nums):
        if self.count == len(nums):
            temp = [num for num in nums]
            self.res.append(temp)
            return

        # find two unchosen positions
        originalIndex = -1
        swapIndex = -1

        for i in range(len(nums)):
            if self.used[i]:
                continue
            if originalIndex == -1:
                originalIndex = i
            swapIndex = i

            # make a choice, element nums[originalIndex] chooses the swapIndex position
            nums[originalIndex], nums[swapIndex] = nums[swapIndex], nums[originalIndex]
            self.used[swapIndex] = True
            self.count += 1
            # go to the next level of decision tree
            self.backtrack(nums)
            # undo the choice, restore it as it was
            self.count -= 1
            self.used[swapIndex] = False
            nums[originalIndex], nums[swapIndex] = nums[swapIndex], nums[originalIndex]

func permute(nums []int) [][]int {
	// result list
	res := make([][]int, 0)
	// mark elements as used or not
	used := make([]bool, len(nums))
	// record how many elements have been placed
	count := 0

	var backtrack func([]int)

	// backtracking framework
	backtrack = func(nums []int) {
		if count == len(nums) {
			temp := make([]int, len(nums))
			copy(temp, nums)
			res = append(res, temp)
			return
		}

		// find two unchosen positions
		originalIndex := -1
		swapIndex := -1

		for i := 0; i < len(nums); i++ {
			if used[i] {
				continue
			}
			if originalIndex == -1 {
				originalIndex = i
			}
			swapIndex = i

			// make a choice, element nums[originalIndex] chooses the swapIndex position
			swap(nums, originalIndex, swapIndex)
			used[swapIndex] = true
			count++
			// go to the next level of the decision tree
			backtrack(nums)
			// undo the choice, restore as it was
			count--
			used[swapIndex] = false
			swap(nums, originalIndex, swapIndex)
		}
	}

	backtrack(nums)
	return res
}

func swap(nums []int, i, j int) {
	nums[i], nums[j] = nums[j], nums[i]
}

var permute = function(nums) {
    // result list
    var res = [];
    // mark elements that have been used
    var used = Array(nums.length).fill(false);
    // record how many elements have been placed
    var count = 0;

    // backtracking algorithm framework
    var backtrack = function(nums) {
        if (count == nums.length) {
            var temp = [];
            for (var num of nums) {
                temp.push(num);
            }
            res.push(temp);
            return;
        }

        // find two unselected positions
        var originalIndex = -1, swapIndex = -1;

        for (var i = 0; i < nums.length; i++) {
            if (used[i]) {
                continue;
            }
            if (originalIndex == -1) {
                originalIndex = i;
            }
            swapIndex = i;

            // make a choice, element nums[originalIndex] selects the swapIndex position
            swap(nums, originalIndex, swapIndex);
            used[swapIndex] = true;
            count++;
            // go to the next level of the decision tree
            backtrack(nums);
            // undo the choice, restore it as it was
            count--;
            used[swapIndex] = false;
            swap(nums, originalIndex, swapIndex);
        }
    }

    var swap = function(nums, i, j) {
        var temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }

    backtrack(nums);
    return res;
};

Rethinking the Subset Problem with the Ball and Box Model

With the previous foundation, I'm going to challenge you further. The article Backtracking Algorithm to Solve Nine Variants of Permutations/Combinations/Subsets has provided code for subset problems.

Taking the most basic subset problem with unique elements and no repetition as an example, I'll directly copy the code here:

class Solution {
    List<List<Integer>> res = new LinkedList<>();
    // record the recursive path of backtracking algorithm
    LinkedList<Integer> track = new LinkedList<>();

    // main function
    public List<List<Integer>> subsets(int[] nums) {
        backtrack(nums, 0);
        return res;
    }

    // core function of backtracking algorithm, traverse the backtracking tree of subset problem
    void backtrack(int[] nums, int start) {

        // pre-order position, the value of each node is a subset
        res.add(new LinkedList<>(track));
        
        // standard framework of backtracking algorithm
        for (int i = start; i < nums.length; i++) {
            // make a choice
            track.addLast(nums[i]);
            // control the traversal of branches through
            // the start parameter to avoid generating
            backtrack(nums, i + 1);
            // undo the choice
            track.removeLast();
        }
    }
}

class Solution {
public:
    vector<vector<int>> res;
    // record the recursive path of backtracking algorithm
    vector<int> track;

    // main function
    vector<vector<int>> subsets(vector<int>& nums) {
        backtrack(nums, 0);
        return res;
    }

    // the core function of backtracking algorithm,
    // traverse the backtracking tree of subset
    void backtrack(vector<int>& nums, int start) {
        // pre-order position, the value of each node is a subset
        res.push_back(track);

        // standard framework of backtracking algorithm
        for (int i = start; i < nums.size(); i++) {
            // make a choice
            track.push_back(nums[i]);
            // control the traversal of branches through
            // the start parameter to avoid generating
            backtrack(nums, i + 1);
            // undo the choice
            track.pop_back();
        }
    }
};

class Solution:
    def __init__(self):
        self.res = []
        # record the recursive path of backtracking algorithm
        self.track = []

    # main function
    def subsets(self, nums: List[int]) -> List[List[int]]:
        self.backtrack(nums, 0)
        return self.res

    # the core function of backtracking algorithm,
    # traverse the backtracking tree of subset
    def backtrack(self, nums, start):
        # preorder position, the value of each node is a subset
        self.res.append(self.track[:])

        # standard framework of backtracking algorithm
        for i in range(start, len(nums)):
            # make a choice
            self.track.append(nums[i])
            # control the traversal of branches through
            # the start parameter to avoid generating
            self.backtrack(nums, i + 1)
            # undo the choice
            self.track.pop()

func subsets(nums []int) [][]int {
    res := make([][]int, 0)
    track := make([]int, 0)

    // backtracking core function, traverse the backtracking tree of subset problem
    var backtrack func(start int)
    backtrack = func(start int) {
        // pre-order position, the value of each node is a subset
        tmp := make([]int, len(track))
        copy(tmp, track)
        res = append(res, tmp)

        // standard framework of backtracking algorithm
        for i:=start; i<len(nums); i++ {
            // make a choice
            track = append(track, nums[i])
            // control the traversal of branches
            // through the start parameter to avoid
            backtrack(i+1)
            // undo the choice
            track = track[:len(track)-1]
        }
    }

    backtrack(0)
    return res
}

var subsets = function(nums) {
    var res = [];
    // record the recursive path of backtracking algorithm
    var track = [];

    var backtrack = function(nums, start) {
        // the pre-order position, the value of each node is a subset
        res.push([...track]);
        for (var i = start; i < nums.length; i++) {
            // make a choice
            track.push(nums[i]);
            // control the traversal of branches through
            // the start parameter to avoid generating
            backtrack(nums, i + 1);
            // undo the choice
            track.pop();
        }
    }

    backtrack(nums, 0);
    return res;
};

// Core code of backtracking algorithm framework
void backtrack(int[] nums, int start) {
    for (int i = start; i < nums.length; i++) {
        track.addLast(nums[i]);
        // Control the growth of branches through the start parameter
        backtrack(nums, i + 1);
        track.removeLast();
    }
}

I will continue to use the Algorithm Visualization Panel to support my answer. Please drag the progress bar to the end to display the entire backtracking tree, then move your mouse horizontally across each level of nodes. Observe the values on the recursive tree nodes and branches, and you can clearly see that it is the bucket's position that is choosing the balls:

class Solution {
    // used to store the results of all subsets
    List<List<Integer>> res;
    // used to store the subset of the current recursive path
    List<Integer> track;

    public List<List<Integer>> subsets(int[] nums) {
        res = new ArrayList<>();
        track = new ArrayList<>();
        backtrack(nums, 0);
        return res;
    }

    void backtrack(int[] nums, int i) {
        if (i == nums.length) {
            res.add(new ArrayList<>(track));
            return;
        }

        // make the first choice, the element is in the subset
        track.add(nums[i]);
        backtrack(nums, i + 1);
        // undo the choice
        track.remove(track.size() - 1);

        // make the second choice, the element is not in the subset
        backtrack(nums, i + 1);
    }
}

class Solution {
public:
    // used to store the results of all subsets
    vector<vector<int>> res;
    // used to store the subset of the current recursive path
    vector<int> track;

    vector<vector<int>> subsets(vector<int>& nums) {
        backtrack(nums, 0);
        return res;
    }

    void backtrack(vector<int>& nums, int i) {
        if (i == nums.size()) {
            res.push_back(track);
            return;
        }

        // make the first choice, the element is in the subset
        track.push_back(nums[i]);
        backtrack(nums, i + 1);
        // undo the choice
        track.pop_back();

        // make the second choice, the element is not in the subset
        backtrack(nums, i + 1);
    }
};

class Solution:
    # used to store the results of all subsets
    res = []
    # used to store the subset of the current recursive path
    track = []

    def subsets(self, nums):
        self.res = []
        self.track = []
        self.backtrack(nums, 0)
        return self.res

    def backtrack(self, nums, i):
        if i == len(nums):
            self.res.append(self.track[:])
            return

        # make the first choice, the element is in the subset
        self.track.append(nums[i])
        self.backtrack(nums, i + 1)
        # undo the choice
        self.track.pop()

        # make the second choice, the element is not in the subset
        self.backtrack(nums, i + 1)

func subsets(nums []int) [][]int {
    // used to store all subsets' results
    var res [][]int
    // used to store the subset of the current recursive path
    var track []int


    var backtrack func(nums []int, i int)
    backtrack = func(nums []int, i int) {
        if i == len(nums) {
            subset := make([]int, len(track))
            copy(subset, track)
            res = append(res, subset)
            return
        }

        // make the first choice, the element is in the subset
        track = append(track, nums[i])
        backtrack(nums, i+1)
        // undo the choice
        track = track[:len(track)-1]

        // make the second choice, the element is not in the subset
        backtrack(nums, i+1)
    }

    backtrack(nums, 0)
    return res
}

var subsets = function(nums) {
    // used to store all subsets' results
    var res = [];
    // used to store the subset of the current recursive path
    var track = [];

    // Inner function for backtracking
    var backtrack = function(nums, i) {
        if (i == nums.length) {
            res.push([...track]);
            return;
        }

        // make the first choice, the element is in the subset
        track.push(nums[i]);
        backtrack(nums, i + 1);
        // undo the choice
        track.pop();

        // make the second choice, the element is not in the subset
        backtrack(nums, i + 1);
    };

    // Start backtracking
    backtrack(nums, 0);
    
    return res;
};

I continue to use the Algorithm Visualization Panel to demonstrate my answer. Please drag the progress bar to the end to display the entire backtracking tree, then move your mouse over the nodes to observe the values on the recursive tree nodes and branches:

This also explains why the number of all subsets (power set) is 2^n. Each element has two choices: either it is in the subset or it is not. Therefore, its recursive tree is a full binary tree with a total of 2^n leaf nodes.

Conclusion

To echo the beginning, let's restate the conclusions. You should understand them better now.

1. The essence of the exhaustive thinking pattern in backtracking algorithms is the "Ball and Box Model." All backtracking algorithms originate from this model; there is no other way.

Go ahead and solve 100 backtracking algorithm problems and see if there are any surprises. If there are, you can come and challenge me.

2. The Ball and Box Model inherently has two exhaustive perspectives: the "ball" perspective and the "box" perspective, corresponding to two different ways of writing code.

Brute-force enumeration is so simple and dull. It may look fancy, but in reality, there are only two perspectives.

3. Theoretically, both perspectives are essentially the same. However, when it comes to specific code implementation, the complexity of the two approaches may differ.

Further思考, why does the "box" perspective, which involves indices selecting elements, allow us to optimize the used array using the swap method?

Because indices are easy to handle. If you let each index select elements in ascending order, a start variable can act as a dividing line to separate selected and unselected elements.

Conversely, if you let elements select indices, you would need an additional data structure to record which indices have been selected, thereby increasing the space complexity.

So, while both perspectives are mathematically equivalent in the initial mathematical analysis, their optimal complexity may differ when it comes to code implementation.

Finally, a悬念: Is the "Ball and Box Model" only used when writing backtracking algorithms?

You can read Two Perspectives of Dynamic Programming Algorithms and ponder this question.