Follow-up: Quick Sort Implementation and Applications

In the previous article Detailed Explanation of Merge Sort Algorithm, the principles and applications of the merge sort algorithm were described from the perspective of binary trees. Many readers found it ingenious. So, I will capitalize on this momentum and today, continue to explain the principles and applications of the quicksort algorithm using the perspective of binary trees.

QuickSort Algorithm Approach

First, let's take a look at the code framework of quicksort:

void sort(int[] nums, int lo, int hi) {
    if (lo >= hi) {
        return;
    }
    // ****** pre-order position ******
    // partition the nums[lo..hi], put nums[p] in the right position
    // such that nums[lo..p-1] <= nums[p] < nums[p+1..hi]
    int p = partition(nums, lo, hi);

    // recursively partition the left and right subarrays
    sort(nums, lo, p - 1);
    sort(nums, p + 1, hi);
}

void sort(int nums[], int lo, int hi) {
    if (lo >= hi) {
        return;
    }
    // ****** pre-order position ******
    // partition the nums[lo..hi], put nums[p] in the right position
    // such that nums[lo..p-1] <= nums[p] < nums[p+1..hi]
    int p = partition(nums, lo, hi);

    // recursively partition the left and right subarrays
    sort(nums, lo, p - 1);
    sort(nums, p + 1, hi);
}

def sort(nums: List[int], lo: int, hi: int):
    if lo >= hi:
        return
    # ****** pre-order position ******
    # partition the nums[lo..hi], put nums[p] in the right position
    # such that nums[lo..p-1] <= nums[p] < nums[p+1..hi]
    p = partition(nums, lo, hi)

    # recursively partition the left and right subarrays
    sort(nums, lo, p - 1)
    sort(nums, p + 1, hi)

func sort(nums []int, lo int, hi int) {
    if lo >= hi {
        return
    }
    // ****** pre-order position ******
    // partition the nums[lo..hi], put nums[p] in the right position
    // such that nums[lo..p-1] <= nums[p] < nums[p+1..hi]
    p := partition(nums, lo, hi)

    // recursively partition the left and right subarrays
    sort(nums, lo, p-1)
    sort(nums, p+1, hi)
}

var sort = function(nums, lo, hi) {
    if (lo >= hi) {
        return;
    }
    // ****** pre-order position ******
    // partition the nums[lo..hi], put nums[p] in the right position
    // make nums[lo..p-1] <= nums[p] < nums[p+1..hi]
    var p = partition(nums, lo, hi);

    // recursively partition the left and right subarrays
    sort(nums, lo, p - 1);
    sort(nums, p + 1, hi);
};

In fact, if you compare them, you'll find that quicksort is essentially a preorder traversal of a binary tree:

// Binary tree traversal framework
void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    // ***** Pre-order position *****
    print(root.val);
    // *******************
    traverse(root.left);
    traverse(root.right);
}

// Binary tree traversal framework
void traverse(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    // ***** Pre-order position *****
    cout << root->val << endl;
    // *******************
    traverse(root->left);
    traverse(root->right);
}

# Binary tree traversal framework
def traverse(root: TreeNode):
    if not root:
        return
    # Pre-order position
    print(root.val)
    traverse(root.left)
    traverse(root.right)

// Binary tree traversal framework
func traverse(root *TreeNode) {
    if root == nil {
        return
    }
    // Pre-order position
    fmt.Println(root.Val)
    traverse(root.Left)
    traverse(root.Right)
}

// Binary tree traversal framework
var traverse = function(root) {
    if (root === null) {
        return;
    }
    // ***** Pre-order position *****
    console.log(root.val);
    // *******************
    traverse(root.left);
    traverse(root.right);
};

Earlier, the article Merge Sort Explained summarized merge sort in one sentence: First, sort the left half of the array, then sort the right half, and finally merge the two halves.

I also asked a question: try to summarize quick sort in one sentence. Here is my answer:

Quick sort sorts one element first, then sorts the remaining elements.

Why do I say this? Let me explain.

The core of quick sort is the partition function. The purpose of partition is to find a split point p in nums[lo..hi]. By swapping elements, all elements in nums[lo..p-1] are less than or equal to nums[p], and all elements in nums[p+1..hi] are greater than nums[p]:

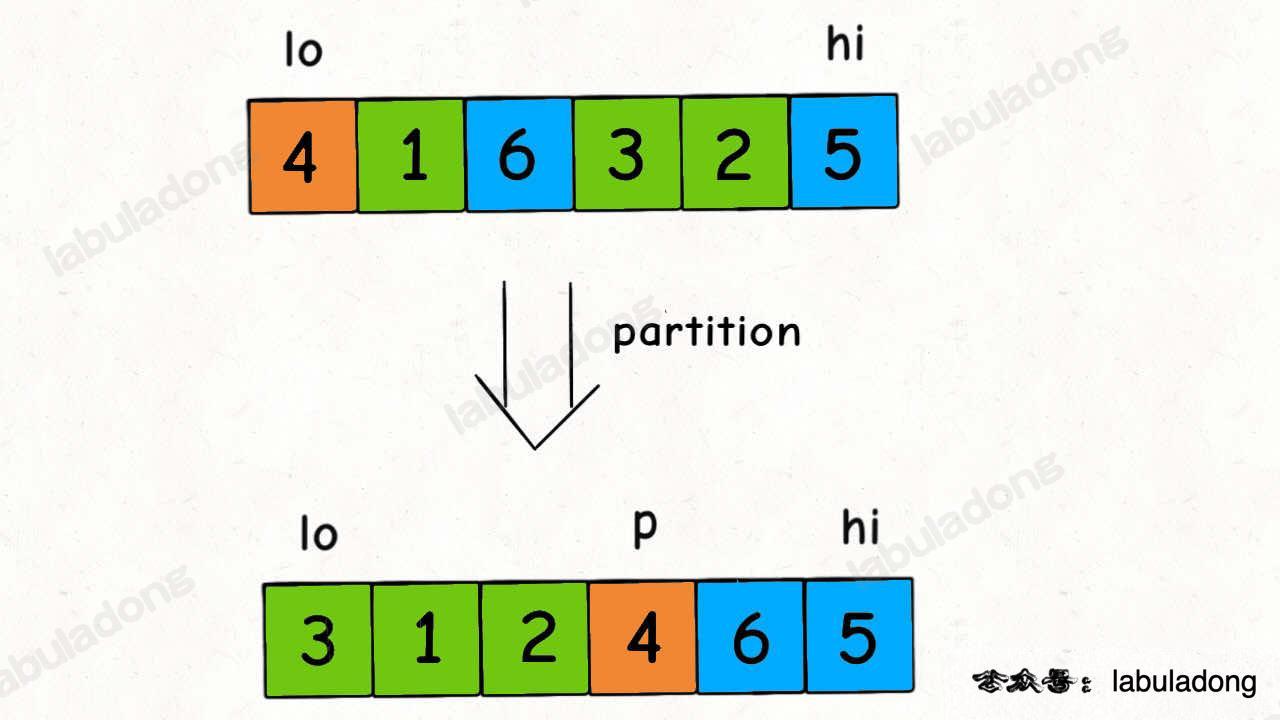
The elements on the left of an element are all smaller than it; the elements on the right are all larger. What does this mean? It means this element is already in the correct position.

So, what the partition function really does is to put nums[p] in its sorted place.

One element is sorted. What about the rest? Just sort the remaining elements.

What are the remaining elements? The left part and the right part. Go ahead, use recursion on the subarrays, and use partition to sort them as well.

From a binary tree point of view, we can think of the subarray nums[lo..hi] as the values on a binary tree node, and the sort function as the traversal function of the tree.

Following the preorder traversal of a binary tree, the process of quick sort is shown in the GIF below:

Implementation of Quicksort

Complexity Analysis and Other Key Points

Quick Select Algorithm