String Multiplication Calculation
This article will resolve
| LeetCode | Difficulty |
|---|---|
| 43. Multiply Strings | 🟠 |
For small numbers, you can use the operators provided by your programming language to do calculations. But if the numbers are very large, the data type might overflow. One solution is to input the numbers as strings, then simulate the multiplication process we learned in elementary school, and use strings to represent the result.
Let's look at LeetCode problem 43, "Multiply Strings":
43. Multiply Strings | LeetCode | 🟠
Given two non-negative integers num1 and num2 represented as strings, return the product of num1 and num2, also represented as a string.
Note: You must not use any built-in BigInteger library or convert the inputs to integer directly.
Example 1:
Input: num1 = "2", num2 = "3" Output: "6"
Example 2:
Input: num1 = "123", num2 = "456" Output: "56088"
Constraints:
1 <= num1.length, num2.length <= 200num1andnum2consist of digits only.- Both
num1andnum2do not contain any leading zero, except the number0itself.
Note that num1 and num2 can be very long, so you can't just convert them to integers and multiply. The only way is to simulate the manual multiplication process.
For example, if you want to calculate 123 × 45 by hand, you would do it like this:

First, calculate 123 × 5, then 123 × 4, and finally add them with the correct offset. This is very easy for elementary school students. But can you turn this calculation process into a set of algorithm steps that a computer can follow?
In this simple process, there is multiplication with carry, addition with offset, and addition with carry. There are also some small problems. For example, multiplying two two-digit numbers may get a three- or four-digit result. How can you handle this in a standard way? This is the magic of algorithms. If you don't think like a computer, even simple problems can't be automated.
First, even this manual process is a bit "advanced." We can break it down even more. The process of 123 × 5 and 123 × 4 can be split into smaller steps, and then add them at the end:
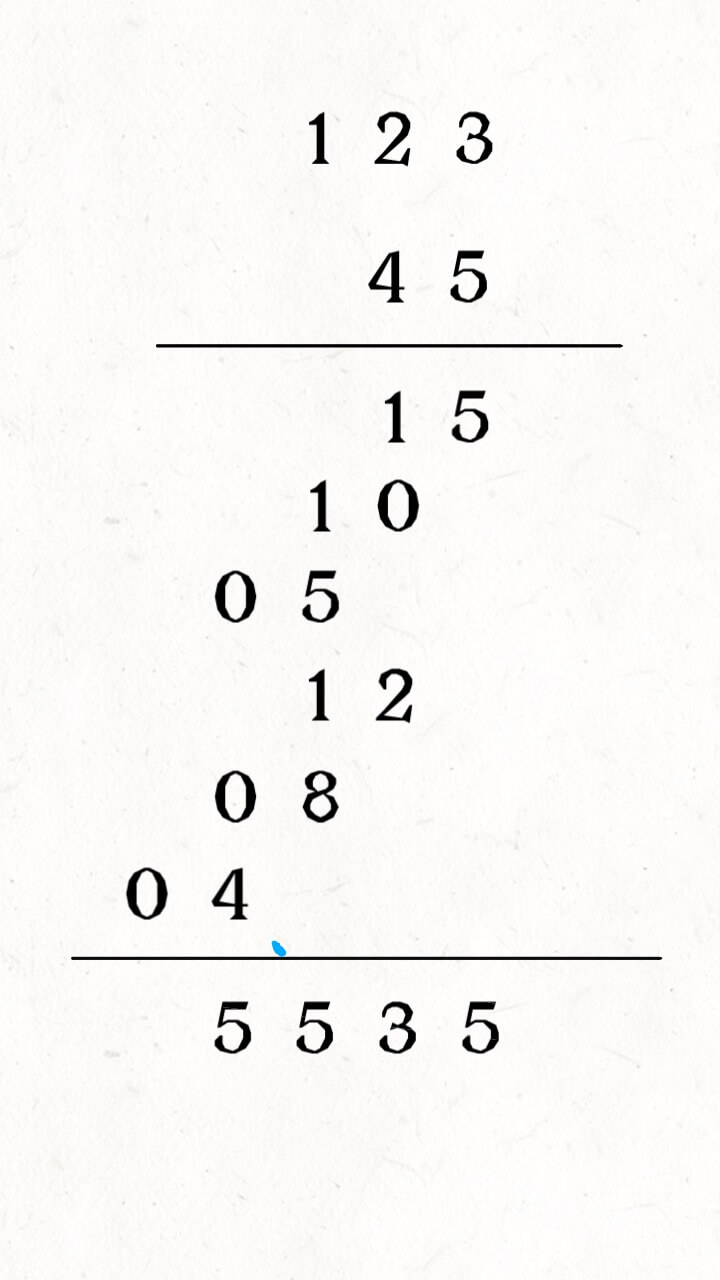
Right now, 123 is not a large number. But if it is very big, you can't directly calculate the product. We can use an array to collect the result as we add up the products:
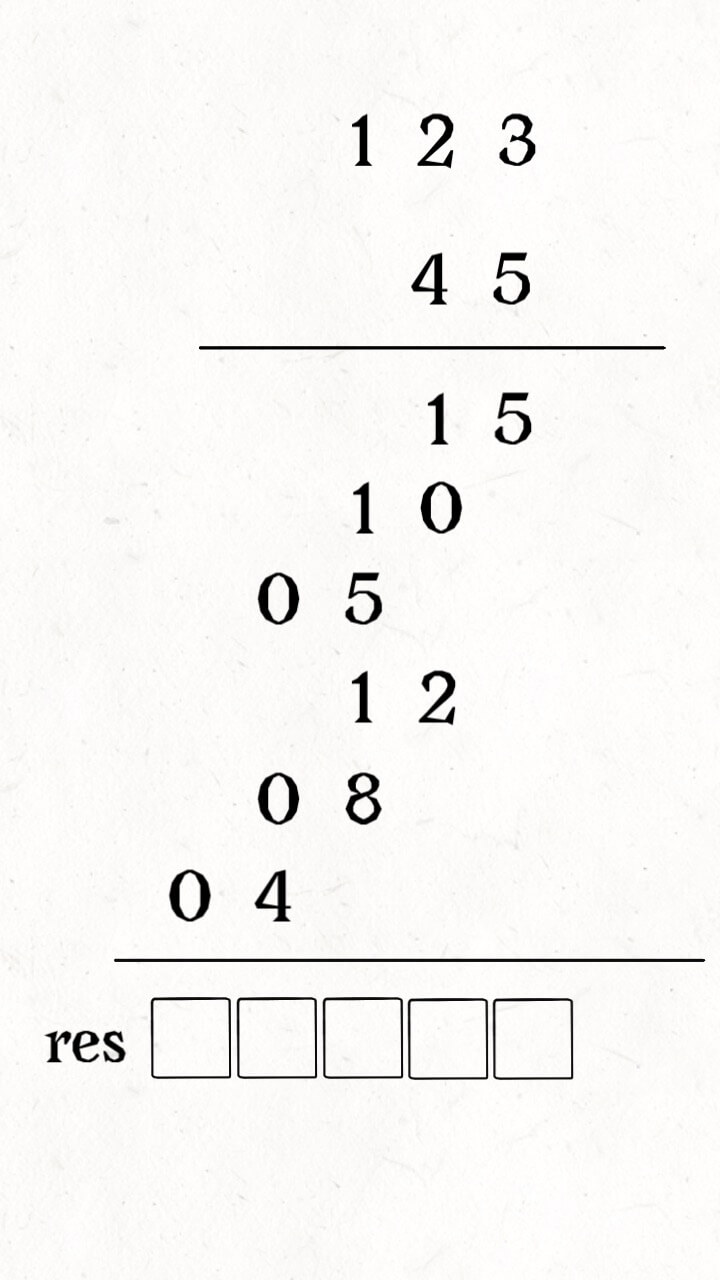
The whole process works like this: use two pointers i and j to walk through num1 and num2, calculate the products, and add the products to the correct position in res, as shown in this GIF:
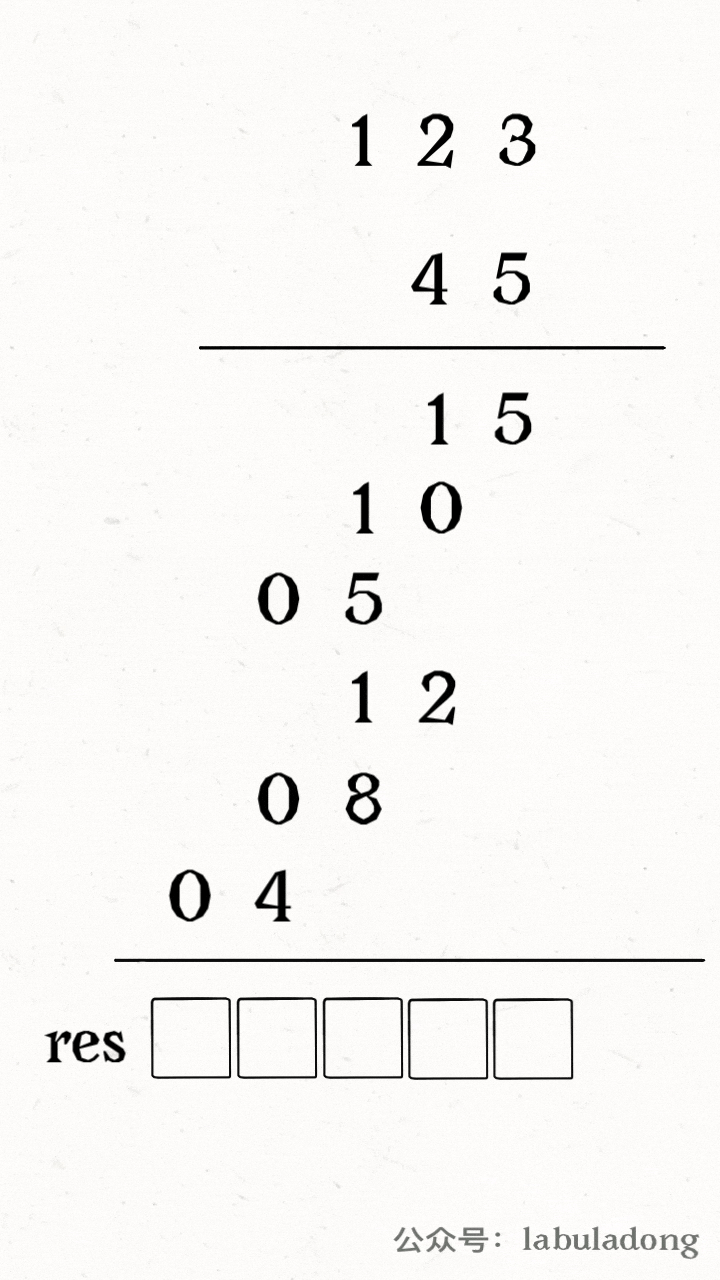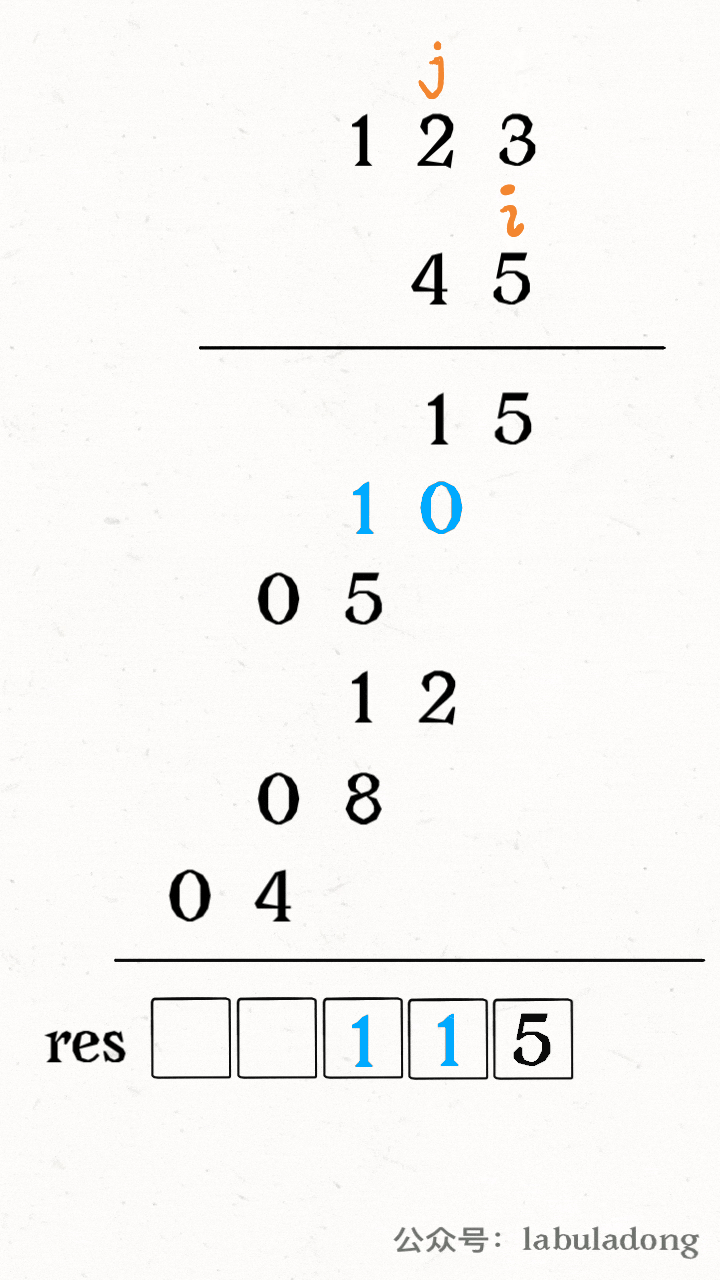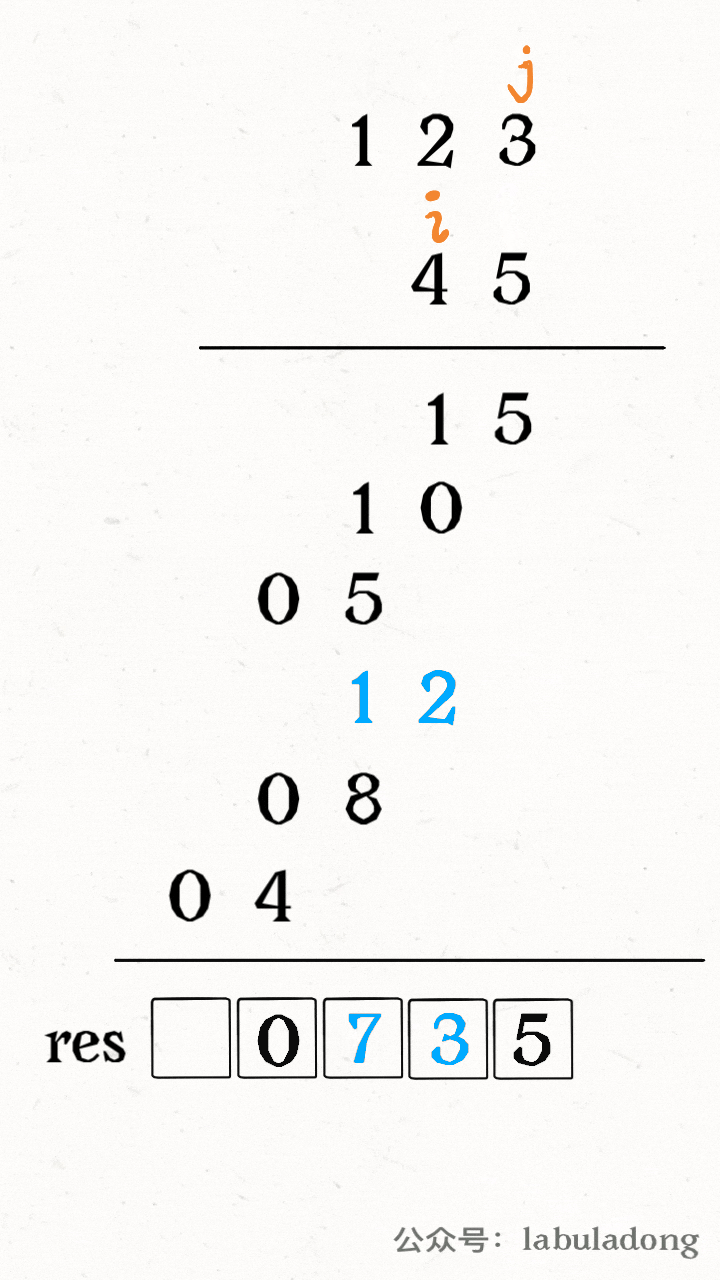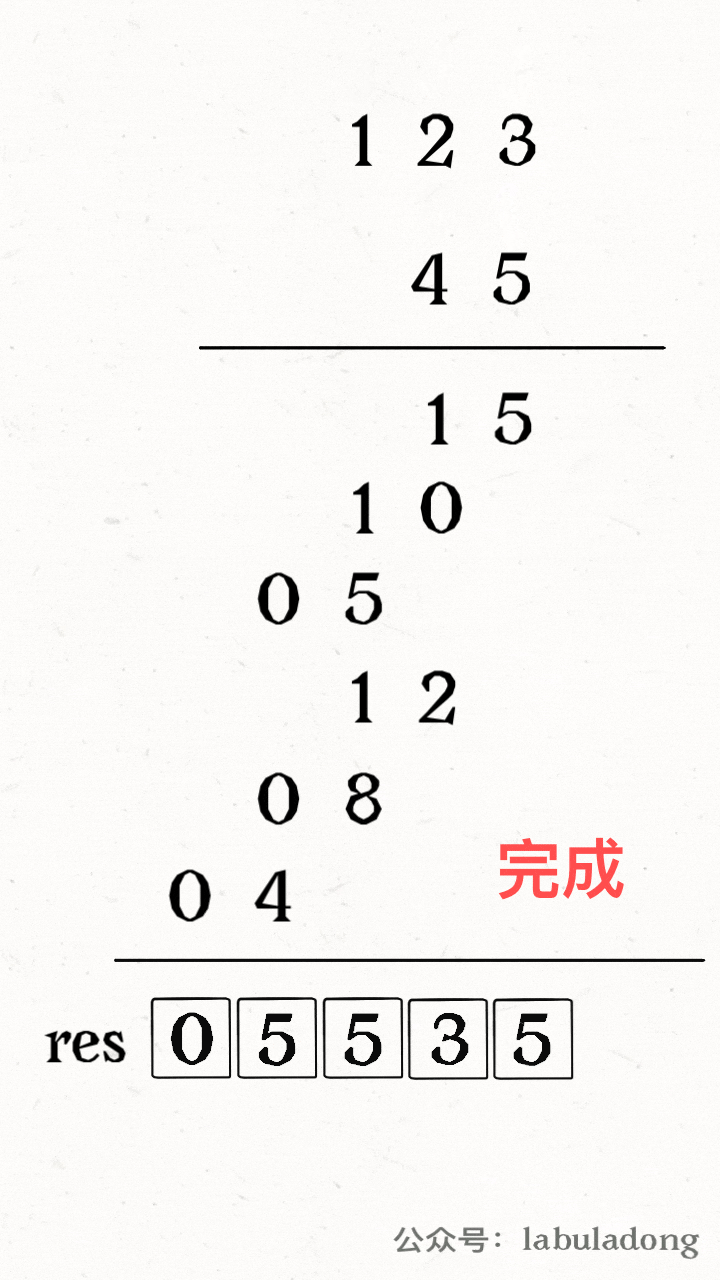
Now there is a key question: how do you add the product to the correct position in res? Or, how do you find the right index in res using i and j?
If you look closely, you will see that the product of num1[i] and num2[j] should go to res[i+j] and res[i+j+1].

Once you understand this, you can write code to simulate this process:
class Solution {
public String multiply(String num1, String num2) {
int m = num1.length(), n = num2.length();
// the result can be at most m + n digits
int[] res = new int[m + n];
// start multiplying from the least significant digit
for (int i = m - 1; i >= 0; i--) {
for (int j = n - 1; j >= 0; j--) {
int mul = (num1.charAt(i) - '0') * (num2.charAt(j) - '0');
// the product is at the corresponding index in res
int p1 = i + j, p2 = i + j + 1;
// add to res
int sum = mul + res[p2];
res[p2] = sum % 10;
res[p1] += sum / 10;
}
}
// the leading zeros that might exist in the result (unused digits)
int i = 0;
while (i < res.length && res[i] == 0)
i++;
// convert the calculation result to a string
StringBuilder str = new StringBuilder();
for (; i < res.length; i++)
str.append(res[i]);
return str.length() == 0 ? "0" : str.toString();
}
}class Solution {
public:
string multiply(string num1, string num2) {
int m = num1.size(), n = num2.size();
// the result can have at most m + n digits
vector<int> res(m + n);
// start multiplying from the least significant digit
for (int i = m - 1; i >= 0; i--) {
for (int j = n - 1; j >= 0; j--) {
int mul = (num1[i] - '0') * (num2[j] - '0');
// the product is at the corresponding index in res
int p1 = i + j, p2 = i + j + 1;
// add to res
int sum = mul + res[p2];
res[p2] = sum % 10;
res[p1] += sum / 10;
}
}
// there may be leading zeros in the result (unused digits)
int i = 0;
while (i < res.size() && res[i] == 0)
i++;
// convert the calculation result to a string
string str;
for (; i < res.size(); i++)
str.push_back(res[i]+'0');
return str.empty() ? "0" : str;
}
};class Solution:
def multiply(self, num1, num2):
m, n = len(num1), len(num2)
# the result can have at most m + n digits
res = [0] * (m + n)
# start multiplying from the least significant digit
for i in reversed(range(m)):
for j in reversed(range(n)):
mul = (ord(num1[i]) - ord('0')) * (ord(num2[j]) - ord('0'))
# the product is at the corresponding index in res
p1, p2 = i + j, i + j + 1
# add to res
summ = mul + res[p2]
res[p2] = summ % 10
res[p1] += summ // 10
# there may be leading zeros in the result (unused digits)
i = 0
while i < len(res) and res[i] == 0:
i += 1
# convert the calculation result to a string
str_res = ''.join(str(x) for x in res[i:])
return "0" if not str_res else str_resfunc multiply(num1 string, num2 string) string {
m, n := len(num1), len(num2)
// the result can have at most m + n digits
res := make([]int, m + n)
// start multiplying from the least significant digit
for i := m - 1; i >= 0; i-- {
for j := n - 1; j >= 0; j-- {
mul := int(num1[i] - '0') * int(num2[j] - '0')
// the product is at the corresponding index in res
p1, p2 := i + j, i + j + 1
// add to res
sum := mul + res[p2]
res[p2] = sum % 10
res[p1] += sum / 10
}
}
// possible leading zeros in the result (unused digits)
i := 0
for i < len(res) && res[i] == 0 {
i++
}
// convert the calculation result to a string
var str strings.Builder
for ; i < len(res); i++ {
str.WriteString(strconv.Itoa(res[i]))
}
if str.String() == "" {
return "0"
}
return str.String()
}var multiply = function(num1, num2) {
let m = num1.length, n = num2.length;
// the result can have at most m + n digits
let res = new Array(m + n).fill(0);
// start multiplying from the least significant digit
for (let i = m - 1; i >= 0; i--) {
for (let j = n - 1; j >= 0; j--) {
let mul = (num1[i] - '0') * (num2[j] - '0');
// the product is at the corresponding index in res
let p1 = i + j, p2 = i + j + 1;
// add to res
let sum = mul + res[p2];
res[p2] = sum % 10;
res[p1] += Math.floor(sum / 10);
}
}
// the leading zeros in the result (unused digits)
let i = 0;
while (i < res.length && res[i] == 0)
i++;
// convert the calculation result to a string
let str = "";
for (; i < res.length; i++)
str += res[i];
return str.length == 0 ? "0" : str;
}Now, the string multiplication algorithm is done.
To sum up, the ways we usually think about calculation are actually hard for computers. The arithmetic processes we are used to are not complicated, but it's not easy to turn them into code. Algorithms need to simplify the process. Here, we get the result by adding as we calculate.
There is a saying: "Don't fall into fixed ways of thinking. Don't be too mechanical. Be creative." But I think being mechanical is not always bad. It can make things faster and reduce mistakes. Algorithms are a set of mechanical thinking steps. Only by being mechanical can computers help us solve hard problems!
Maybe algorithm is just a way to find fixed ways of thinking. I hope this article helps you.