Tricks to Traverse a 2D Array
This article will resolve
| LeetCode | Difficulty |
|---|---|
| 151. Reverse Words in a String | 🟠 |
| 48. Rotate Image | 🟠 |
| 54. Spiral Matrix | 🟠 |
| 59. Spiral Matrix II | 🟠 |
| 61. Rotate List | 🟠 |
Some readers say that after reading many articles on this site, they have mastered the framework thinking and can solve most problems that have common patterns.
But framework thinking is not always enough. Some special skills are easy for people who know them, but hard for people who don't. You can only learn and summarize these skills by practicing more problems.
In this article, I will share some clever tricks for 2D arrays. Just keep them in mind, so you won’t get confused when you see similar problems in the future.
Rotate Matrix Clockwise/Counterclockwise
Rotating a 2D array is a common coding problem. LeetCode problem 48 “Rotate Image” is a classic example:
48. Rotate Image | LeetCode | 🟠
You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise).
You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.
Example 1:
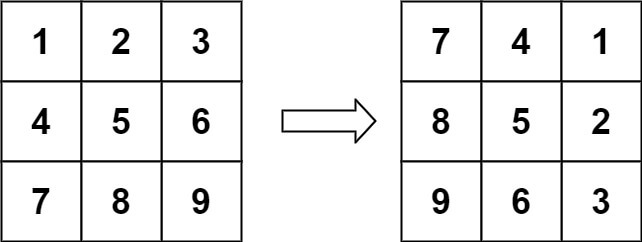
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]] Output: [[7,4,1],[8,5,2],[9,6,3]]
Example 2:
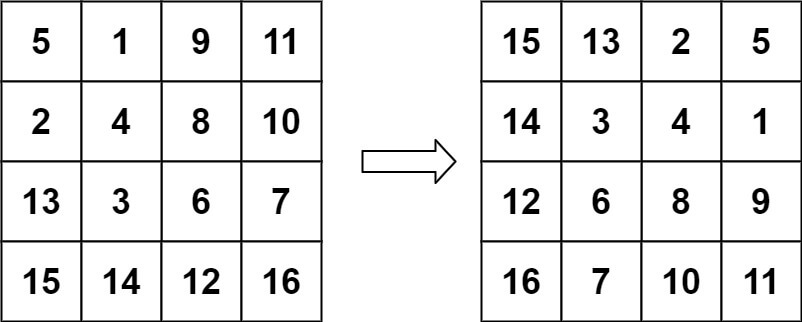
Input: matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] Output: [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
Constraints:
n == matrix.length == matrix[i].length1 <= n <= 20-1000 <= matrix[i][j] <= 1000
The problem is simple: rotate a 2D matrix 90 degrees clockwise. The hard part is to do it “in-place”. The function signature is:
void rotate(int[][] matrix)void rotate(vector<vector<int>>& matrix)def rotate(matrix: List[List[int]]) -> None:func rotate(matrix [][]int) {}var rotate = function(matrix) {}How do you rotate a 2D matrix in-place? At first, it seems complex. You may think you need a tricky algorithm to rotate the matrix “layer by layer”:
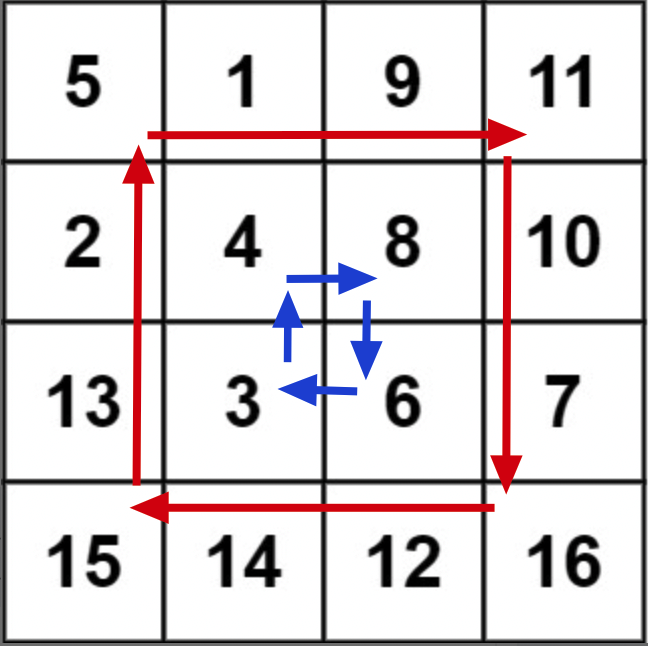
But actually, this problem can be solved in a smarter way. Before we talk about the clever solution, let’s look at another algorithm problem asked by Google:
You are given a string s that contains some words and spaces. Please write an algorithm to reverse the order of all words in-place.
For example, if the input is:
s = "hello world labuladong"Your algorithm should reverse the word order in-place:
s = "labuladong world hello"A common way is to split s by spaces, reverse the list of words, and join them back. But this uses extra space, so it’s not an in-place solution.
The correct way is to first reverse the whole string s:
s = "gnodalubal dlrow olleh"Then reverse each word separately:
s = "labuladong world hello"This achieves in-place reversal of all words. LeetCode problem 151 “Reverse Words in a String” is a similar problem. You can try it yourself.
This trick can be used in other problems too. Check out LeetCode problem 61 “Rotate List”: Given a singly linked list, rotate the list to the right by k places.
For example, input list: 1 -> 2 -> 3 -> 4 -> 5, k = 2. The result should be 4 -> 5 -> 1 -> 2 -> 3, which means move each node right by 2 positions.
Don’t move the nodes one by one. If you think carefully, you just need to move the last k nodes to the front of the list. Get it?
If not, here’s another hint: moving the last k nodes to the front is just like reversing the first n - k nodes and the last k nodes, all in-place, right?
So, this is similar to the in-place reverse of words in a string. You just need to reverse the whole list, then reverse the first n - k nodes and the last k nodes separately, and you get the answer.
Of course, there are some details. For example, k might be greater than the length of the list. So first, you need to find the length n of the list, then take k = k % n. This way, k will not be larger than the list length and the final result will be correct.
Try solving this problem yourself. It’s not hard, so I won’t show code here.
Why did I talk about these two problems?
The point is: sometimes, the obvious way we think about a problem is not the most elegant for a computer. But the most elegant computer solution may not be so intuitive for us. Maybe this is the charm of algorithms.