Introduction to Cryptography
When we talk about passwords, the first thing we think of is the login password for our account. But from the view of cryptography, this is not really a good password.
Why? Because account passwords rely on secrecy: you keep the password in your mind, others don't know it, so they cannot log in to your account.
But cryptography thinks that any "secret" will be leaked one day. So, a good encryption algorithm should not rely on keeping the algorithm secret. Even if you know the algorithm, you should not be able to break it. To put it another way: even if I tell you my encryption method, you still can't figure out my password.
One of the most amazing algorithms is the Diffie-Hellman key exchange. I was surprised when I first learned it. Two people say some numbers in public, and somehow end up with the same secret. But you, as a listener, can't know this secret. We will introduce this algorithm in detail later.
The main goal of cryptography discussed in this article is to solve the problem of encrypting and decrypting information during data transfer. We must assume the data transfer process is unsafe, and all information may be eavesdropped. So, the sender must encrypt the message, and the receiver must know how to decrypt it. But if you let the receiver know how to decrypt, doesn't the eavesdropper also get this information?
Next, we will introduce symmetric encryption, key exchange, asymmetric encryption, digital signature, and public key certificate to see how these methods solve the problem of secure transmission.
1. Symmetric Encryption
Symmetric encryption, also called shared-key encryption, uses the same key to encrypt and decrypt data.
For example, here is a simple way to do symmetric encryption. We know all information can be written as a sequence of 0s and 1s. If you XOR two same bit sequences, you get a result of 0.
So, you can make a random bit sequence with the same length as the original information to use as the key. Then, you XOR the key with the original data to make the encrypted message. To decrypt, you just XOR the encrypted message with the same key, and you get the original information.
This is a simple example, but it has problems. For example, the key must be as long as the original message. If the message is large, the key is also large. Also, making long, truly random bit sequences is expensive.
Of course, many better symmetric encryption algorithms can fix these problems, like the Rijndael algorithm (also called AES), triple DES, and others. These algorithms are strong, with huge key spaces, making brute-force attacks very hard. They are also efficient and fast.
However, the weakness of all symmetric encryption is how to share the key. Since the same key is used for both sending and receiving, the sender must find a way to give the key to the receiver. If an eavesdropper can steal the message, they can also steal the key. Even the best algorithm can't help in this case.
Next, we will introduce two of the most common ways to solve the key sharing problem: the Diffie-Hellman key exchange algorithm and asymmetric encryption.
2. Key Exchange Algorithm
A key is usually a very large number, used by algorithms for encryption and decryption. But the channel is not secure, so any data you send can be stolen. In other words, is there a way for two people to exchange a secret openly, so that the symmetric key can be safely delivered to the other side?
The Diffie-Hellman key exchange algorithm can do this. To be exact, this algorithm does not send a secret securely to the other side, but lets both parties "generate" the same secret in their minds through some shared numbers. This secret is something a third-party eavesdropper cannot generate.
Maybe this is what people call "having a connection" without saying a word.
This algorithm is not very complicated. You can even try it with a friend to share a secret. I will draw its basic flow in a while. But first, you need to know: Not all operations have reverse operations.
The simplest example is a one-way hash function. Given a number a and a hash function f, you can quickly calculate f(a). But if you only have f(a) and f, it's almost impossible to find a. The key exchange algorithm takes advantage of this one-way property.
Now, let's see how the key exchange algorithm works. By practice, we call the two parties Alice and Bob, and the person who tries to steal their communication Hack.
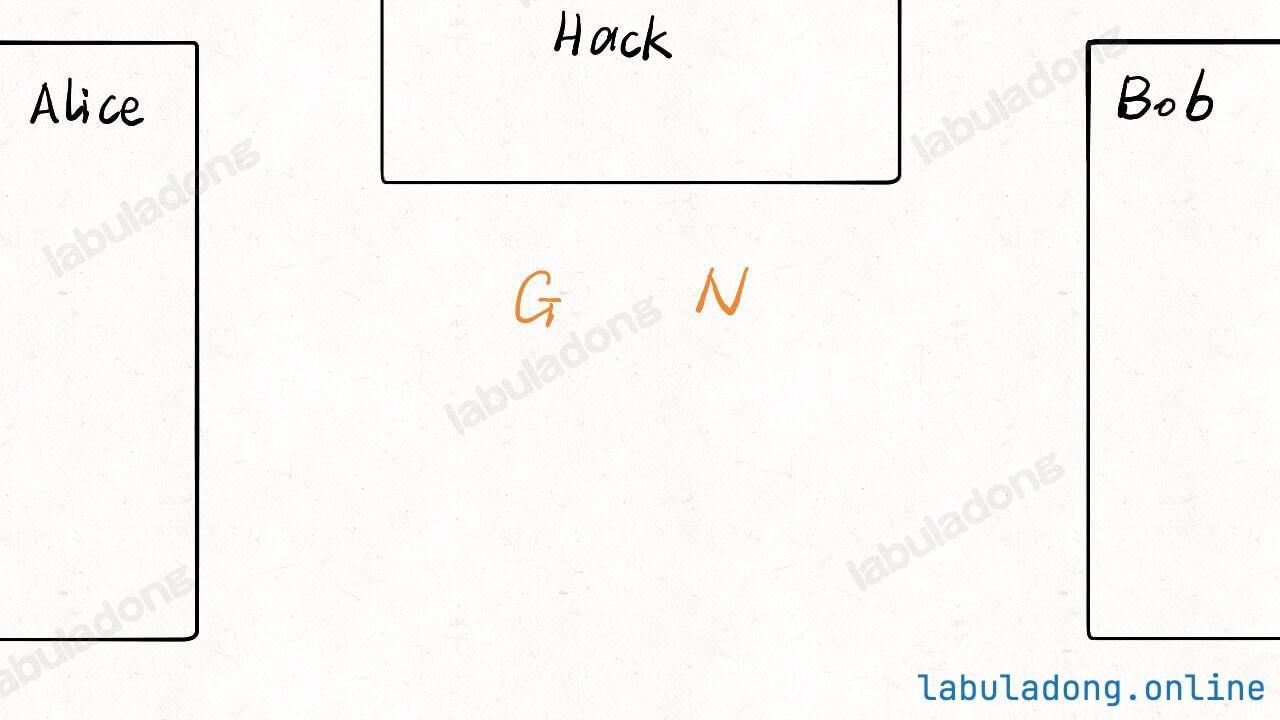
First, Alice and Bob agree on two numbers N and G as the base numbers. This agreement can be eavesdropped by Hack, so let's put these two numbers in the middle, showing that all three know them:
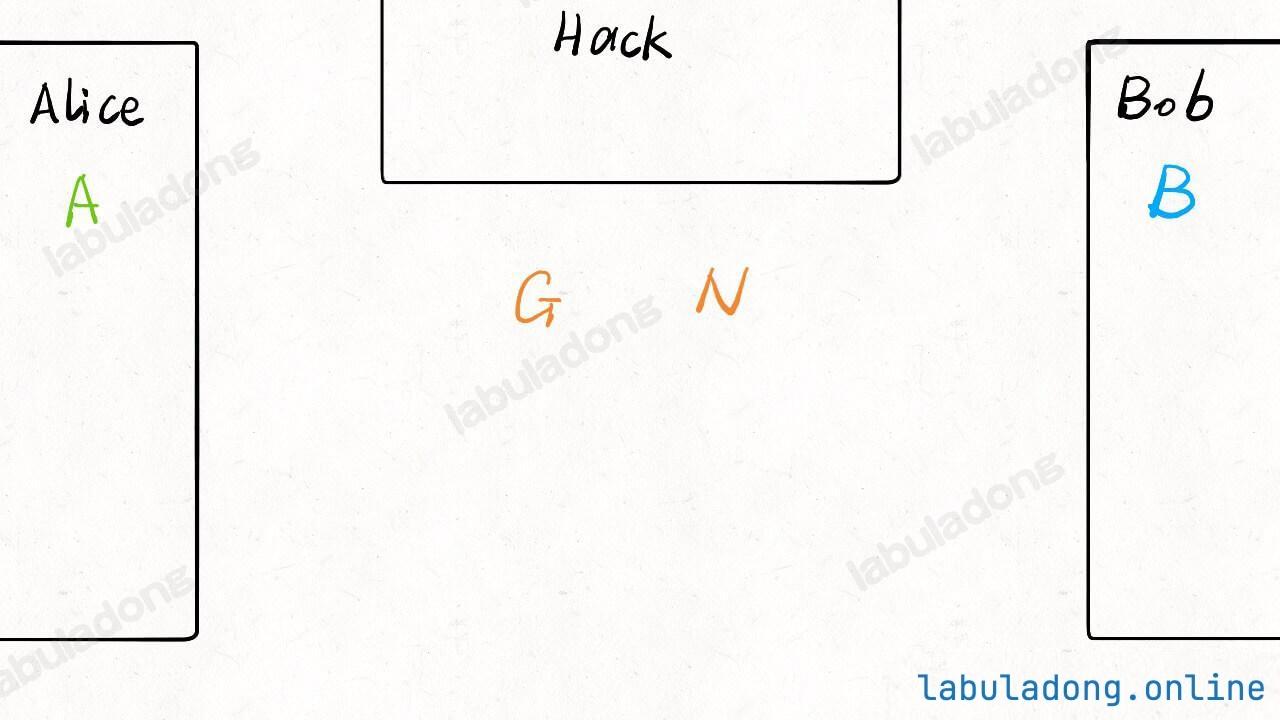
Now, Alice and Bob each think of a number secretly, called A and B:
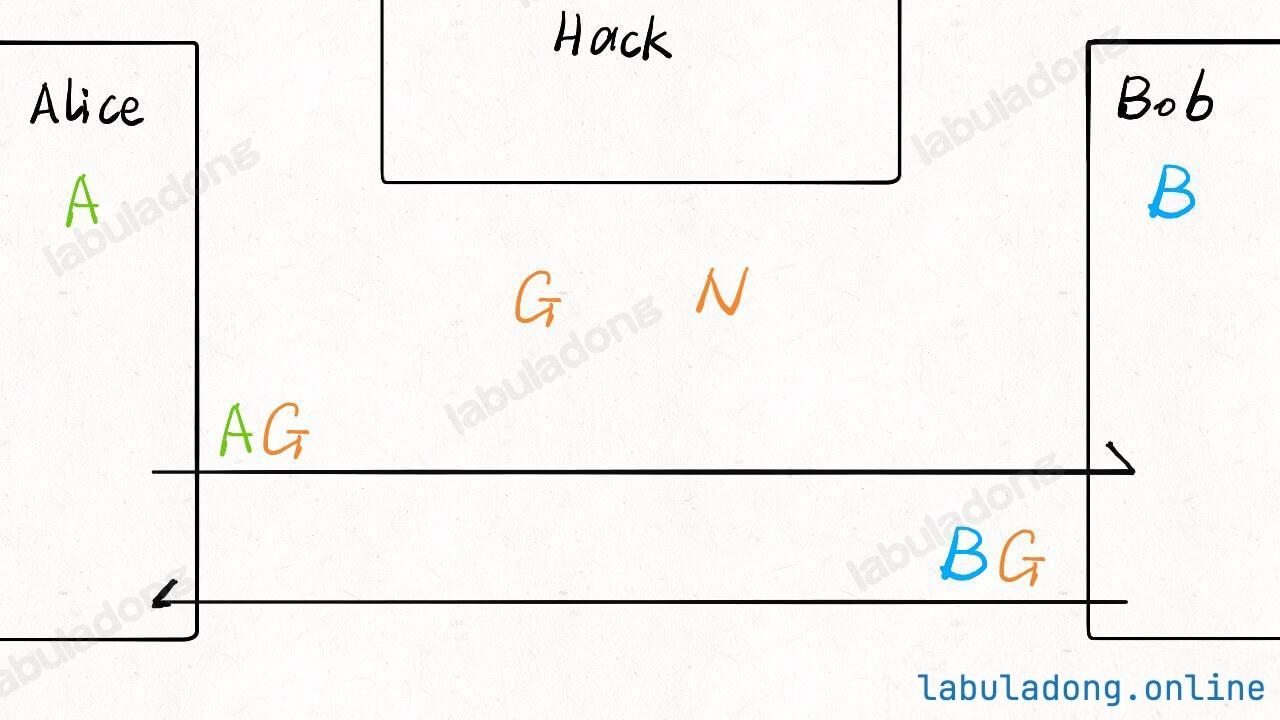
Next, Alice combines her secret number A with G through some operation to get a number AG, and sends it to Bob. Bob does the same with his secret number B and G to get BG, and sends it to Alice:
Now, the status is like this:
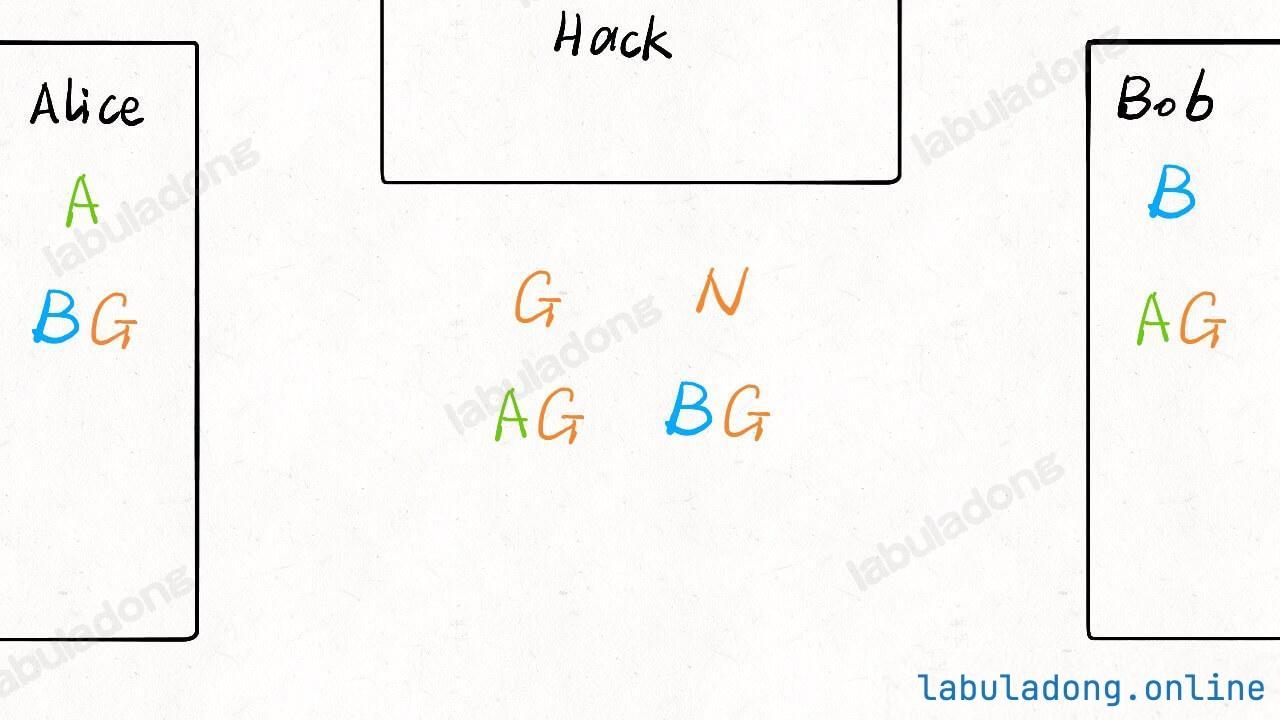
Note, just like the hash function example, knowing AG and G does not let you find out A, and it's the same for BG.
Now, Alice can use BG and her own A to calculate a number ABG. Bob can use AG and his own B to also get ABG. This number is the shared secret for Alice and Bob.
For Hack, even if he gets G, AG, and BG from the communication, he still cannot calculate ABG because the calculation cannot go backwards.
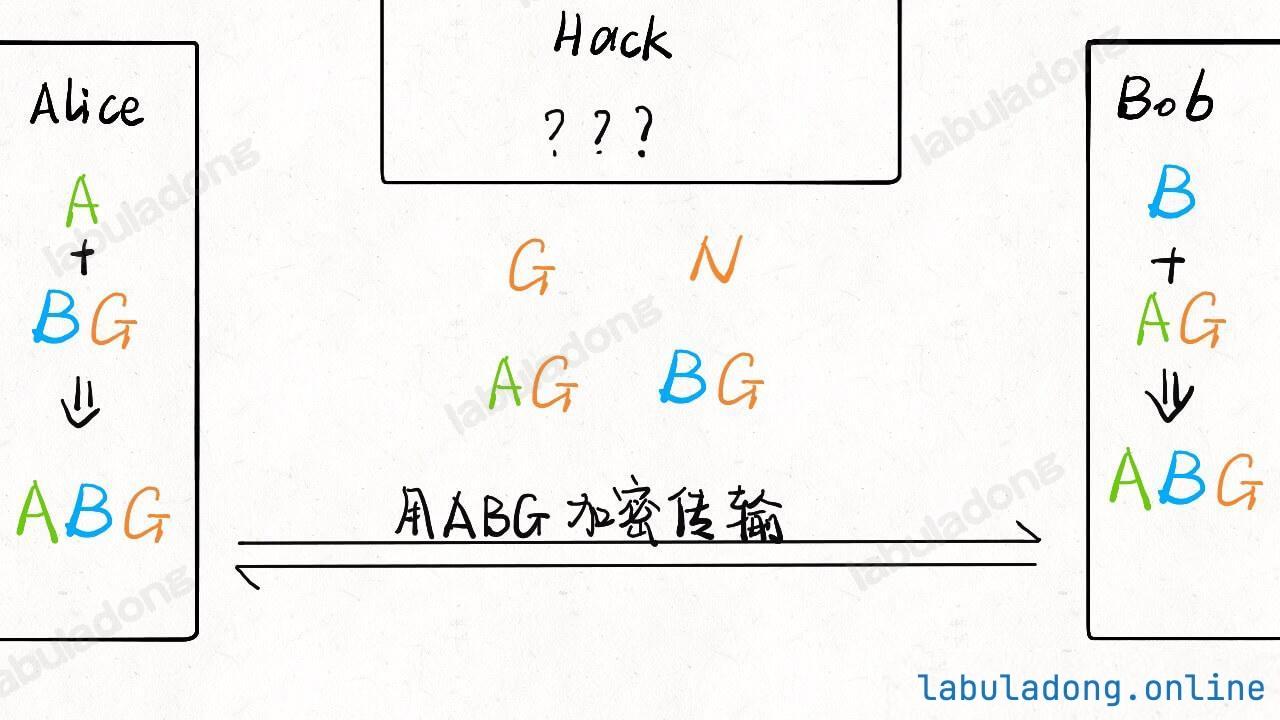
This is the main process. The specific way to pick numbers and do the math can be found easily online. I won't explain it in detail here.
This algorithm can help Alice and Bob get a secret that others cannot find out, even when a third party is listening, and then use it as the key for symmetric encryption.
But Hack can try another way to break it. Instead of simply listening, he pretends to be both Alice and Bob. This is called the "man-in-the-middle attack":
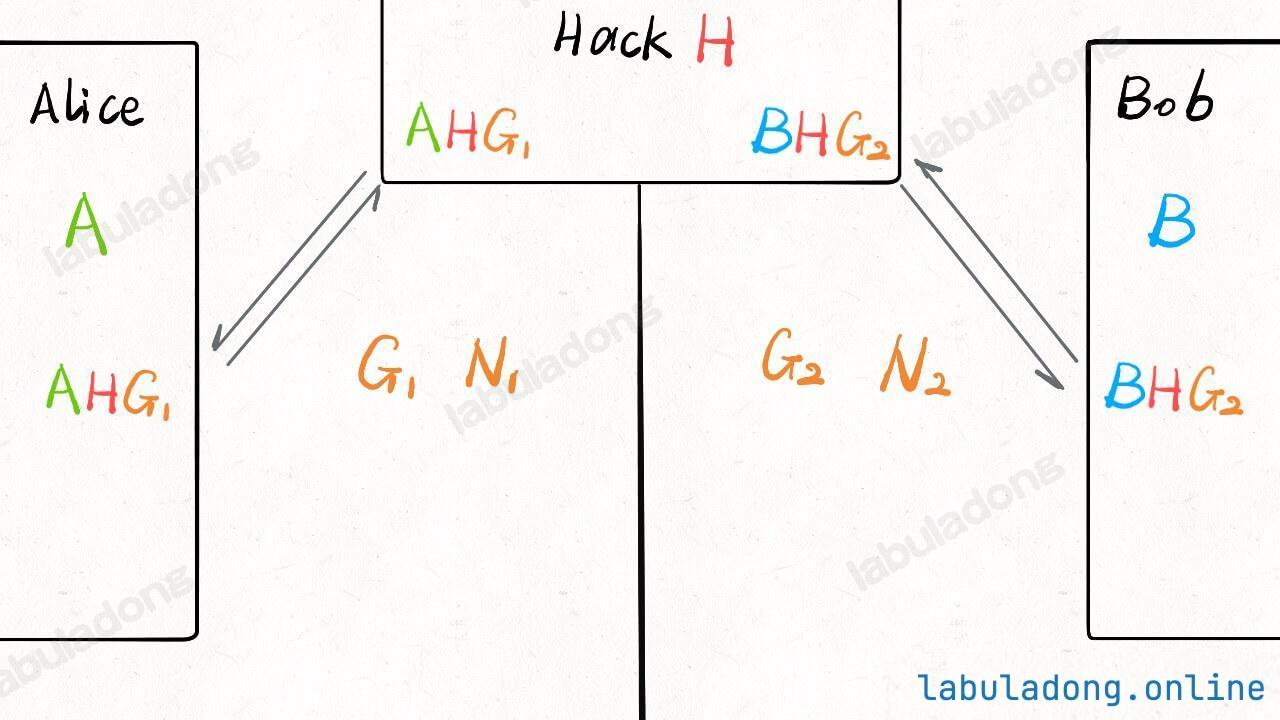
Like this, both parties do not know they are sharing the secret with Hack, so Hack can read or even change the data.
So, the key exchange algorithm does not completely solve the key distribution problem. Its weakness is that it cannot verify the other person’s identity. That’s why people usually check identities before using the key exchange algorithm, for example, by using digital signatures.
3. Asymmetric Encryption
The idea of asymmetric encryption is simple: don't try to secretly transmit the key. Instead, split the key into two parts: a public key for encryption and a private key for decryption. Only share the public key with others. When someone wants to send me data, they use my public key to encrypt it. I can then use my private key to decrypt it. An eavesdropper will have the public key and encrypted data, but they cannot decrypt it without the private key.
Think of it like this: the private key is the key, and the public key is the lock. You can give the lock to anyone, so they can lock up data and send it to you. But only you have the key to unlock it. A common example is the RSA algorithm, which is a classic asymmetric encryption method. The actual implementation is complicated, so I won't explain it here—there are many resources online.
In reality, asymmetric encryption is much slower than symmetric encryption. So, when sending large amounts of data, we don't use the public key to encrypt all the data directly. Instead, we use it to encrypt the symmetric key and send that to the other person. Both sides then use the faster symmetric encryption to send data.
One thing to note is that, like the Diffie-Hellman algorithm, asymmetric encryption can't verify who you are talking to, so it can still be attacked by a man-in-the-middle. For example, if Hack intercepts Bob’s public key, and then sends their own public key to Alice pretending to be Bob, Alice could unknowingly send her secret data encrypted to Hack's public key. Hack can then use their private key to read it.
So, both the Diffie-Hellman algorithm and RSA asymmetric encryption solve the key distribution problem in some way, but they both have similar weaknesses. What’s the difference in how these two methods are used?
Simply put, you can choose which to use based on how they work:
If both sides want to communicate securely using symmetric encryption without sharing the key directly, they can use the Diffie-Hellman algorithm to exchange the key.
If you want anyone to be able to encrypt messages to you, but only you can read them, then use RSA asymmetric encryption and publish your public key.
Next, let’s try to solve the problem of verifying who is sending the message.
4. Digital Signature
Just now we talked about asymmetric encryption. You make your public key open so others can use it to encrypt data and send it to you. Then, only you can use your private key to decrypt it. In fact, the private key can also be used to encrypt data. For the RSA algorithm, only the public key can unlock data encrypted by the private key.
A digital signature uses this feature of asymmetric keys, but the process is the opposite of public key encryption. You still make your public key public, but you use your private key to encrypt data, and then publish the encrypted data. This is a digital signature.
You may ask, what is the point? If anyone with my public key can decrypt my private key’s encryption, why do I need to encrypt and send it?
That’s right, but the role of a digital signature is not to hide the content, but to prove your identity. It proves the data indeed comes from you.
Think about it. If only the matching public key can decrypt what you encrypt with your private key, then when some data can be decrypted with your public key, doesn't it mean you (the one holding the private key) created it?
Of course, the encrypted data is just the signature. The signature should be sent along with the real data. The detailed process is:
- Bob generates a public key and a private key. He publishes the public key and keeps the private key safe.
- Bob uses his private key to encrypt the data as a signature, then publishes the data along with the signature.
- Alice receives the data and the signature. She wants to check if the data really comes from Bob. So, she uses Bob’s public key to decrypt the signature, and compares the result with the received data. If they are the same, it means the data hasn’t been changed and really comes from Bob.
Why is Alice so sure? After all, both the data and the signature can be swapped. The reasons are:
- If anyone changes the data, Alice will find that the decrypted signature does not match the new data.
- If anyone changes the signature, Bob’s public key will decrypt it into meaningless data, which will not match the original data.
- If someone tries to change the data and make a matching new signature, they can't. Because they don’t have Bob’s private key, it’s impossible to create a new valid signature.
In short, digital signatures can prove to some degree where the data comes from. But I say "to some degree" because this can still be attacked by a man-in-the-middle. If the public key is replaced by an attacker when being published, the receiver may do wrong verification. This problem cannot be avoided.
It's a bit funny: digital signatures are a way to verify someone's identity, but the whole process relies on the other side's identity being true in the first place... It is something like the chicken and egg problem. To really confirm someone’s identity, there must be a trusted starting point. Without that, all these steps just move the problem around and don’t really solve it.
5. Public Key Certificate
A certificate is actually just a public key plus a signature, issued by a trusted third-party organization. Introducing a trusted third party is a practical way to solve the trust cycle problem.
The general process of certificate authentication is as follows:
Bob goes to a trusted authority to prove his real identity and provides his public key.
Alice wants to communicate with Bob, so she first asks the authority for Bob’s public key. The authority sends back a certificate, which contains Bob's public key and the authority’s signature on it.
Alice checks the signature to make sure the public key was really sent by the authority and has not been tampered with.
Alice uses this public key to encrypt data and starts communicating with Bob.
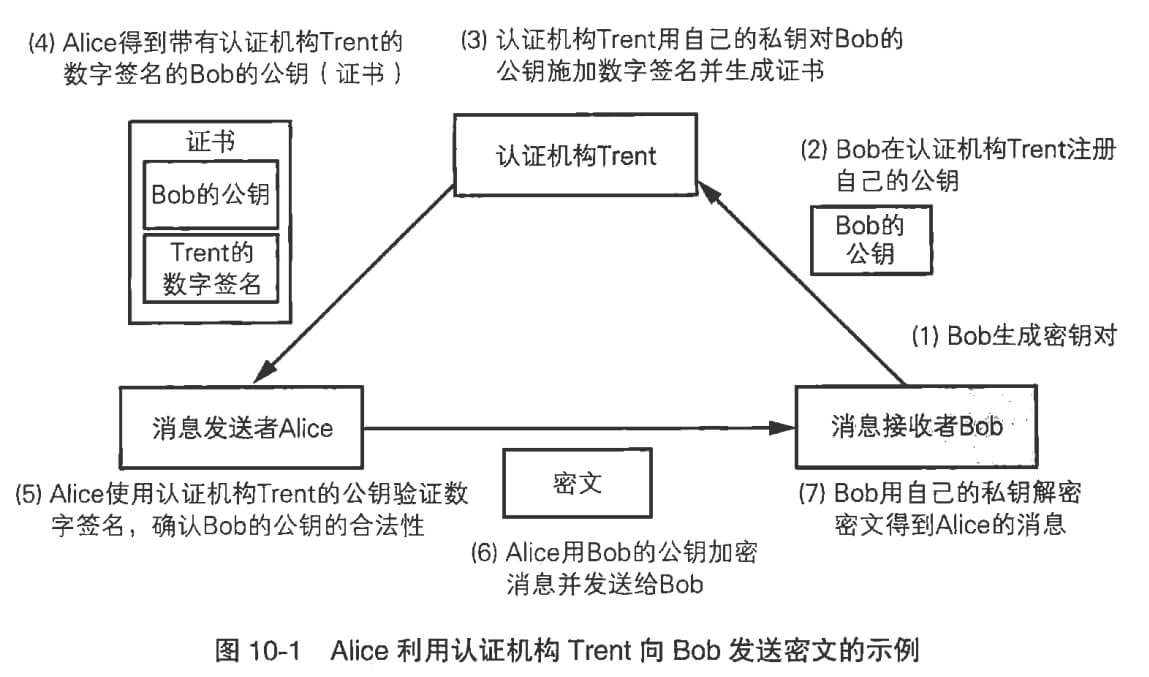
Note
This is just to explain the concept: a certificate only needs to be installed once and is not requested from the authority every time. Usually, the server sends the certificate directly to the client, not the authority.
You might ask: for Alice to verify the certificate's validity with a digital signature, she needs the authority's (trusted) public key. Isn't this another looping trust problem?
Legitimate browsers already have certificates for regular authorities (including their public keys) pre-installed. This lets browsers confirm the authority’s identity, so certificate authentication is trustworthy.
When Bob gives his public key to the authority, he must also give a lot of personal info for identity verification, making this process reliable.
With Bob’s trusted public key, communication between Alice and Bob is fully protected by encryption algorithms and is very secure.
Today’s legitimate websites use the HTTPS protocol, which adds an SSL/TLS security layer between HTTP and TCP. After your browser and the web server complete the TCP handshake, the SSL layer performs its own handshake to exchange security parameters, including the website’s certificate. The browser can then verify the site's identity. After the SSL security layer is set up, all HTTP content is encrypted, keeping your data safe during transfer.
This setup makes traditional man-in-the-middle attacks almost impossible. Attackers can only rely on scams or tricks instead of technology flaws. In fact, these tricks can be very effective. For example, I’ve found that some download websites distribute browsers that not only contain strange bookmarks and website links, but also some non-standard authority certificates. Anyone can apply for a certificate, and untrustworthy certificates can cause serious security risks.
6. Summary
Symmetric encryption algorithms use the same key for encryption and decryption. They are hard to crack and encrypt data quickly, but the key distribution is a problem.
The Diffie-Hellman key exchange algorithm lets both sides agree on a secret key. It solves part of the key distribution problem, but cannot verify the identity of the parties, so it is still vulnerable to man-in-the-middle attacks.
Asymmetric encryption algorithms create a pair of keys. Encryption and decryption work are separated.
RSA is a classic asymmetric encryption algorithm with two uses: If used for encryption, you can publish your public key for others to encrypt data, and only your private key can decrypt it. This keeps data secret. If used for digital signatures, you publish your public key, then use your private key to sign the data. Anyone can use your public key to verify the data was sent by you. However, in both uses, publishing the public key cannot prevent man-in-the-middle attacks.
A public key certificate combines the public key and a digital signature, and is issued by a trusted certificate authority. Most browsers have trusted certificate authorities’ public keys built-in, so public key certificates can effectively prevent man-in-the-middle attacks.
The SSL/TLS security layer in the HTTPS protocol uses several types of encryption together. So, do not install untrusted browsers and do not install certificates from unknown sources.
Cryptography is only a small part of security. Even an HTTPS site verified by an official authority does not mean it is trustworthy. It only means data transmission is secure. Technology alone can never fully protect you. The most important thing is to be careful, increase your security awareness, and handle sensitive data with caution.