Learning Plan for Quick Mastery
Some readers told me that the content on this site is very solid. If you study carefully, you can master data structures and algorithms. But their problem is they do not have enough time. What should they do?
Can you focus on the most important and useful skills first, improve quickly in a short time, and then study more when you have time later? I think this is what many readers need, so I wrote this simple quick mastery plan.
If you have enough time and you are interested in learning algorithms, you can follow the Beginner Plan to study all the content on this site.
If you do not have much time for preparing algorithms, or if you are not sure whether to choose the Beginner Plan or Quick Mastery Plan, do not hesitate, just follow the Quick Mastery Plan. Do not try to learn everything at once. Focus on the content in the quick mastery plan first. If you have more time and interest later, you can come back and learn other content on the site. There is no conflict.
The articles and problems of the quick mastery plan are already collected in this roadmap. Click the nodes on the roadmap to open related tutorials and problem lists, which helps you track your progress and review:
Note
The roadmap is a tree structure, but the directory list is a linear structure. So, the order in the roadmap is different from the list below, but the content is exactly the same. You can choose whichever format you like to study.
Algorithm Quick Mastery Roadmap
About Problem Lists
Many readers often ask about company-specific problem lists, so I want to talk more about it here.
The quick mastery plan includes must-know algorithm techniques and classic algorithm problems. It is not limited to any one company's problem list. The goal is to really master algorithms, so you can solve medium-level, common algorithm problems by yourself, not just rely on luck or memory to finish certain problem lists.
Some readers want to prepare for algorithms by just practicing company problem lists directly. This is not correct. My suggestion is, first master the common algorithm templates, and then do problem lists as the next step.
Different companies have different problem lists and difficulty levels, but the core algorithm templates are almost the same. Once you master the templates, you can finish a problem list in just two or three hours. There is nothing special.
Problem lists have only two main benefits:
1. You can know the problem types and algorithm difficulty for the company ahead of time. For example, if your company clearly says it will not test dynamic programming, you can skip the dynamic programming part in this directory and focus your time on other algorithm techniques.
2. They are helpful for review. After learning the algorithm templates, you can solve problems on your own. At this point, you can do a few rounds of the problem list to check your learning and strengthen your understanding.
It may look like there are a lot of problems in the quick mastery plan, but most are template problems. After you finish the tutorials, you can solve them all without extra practice.
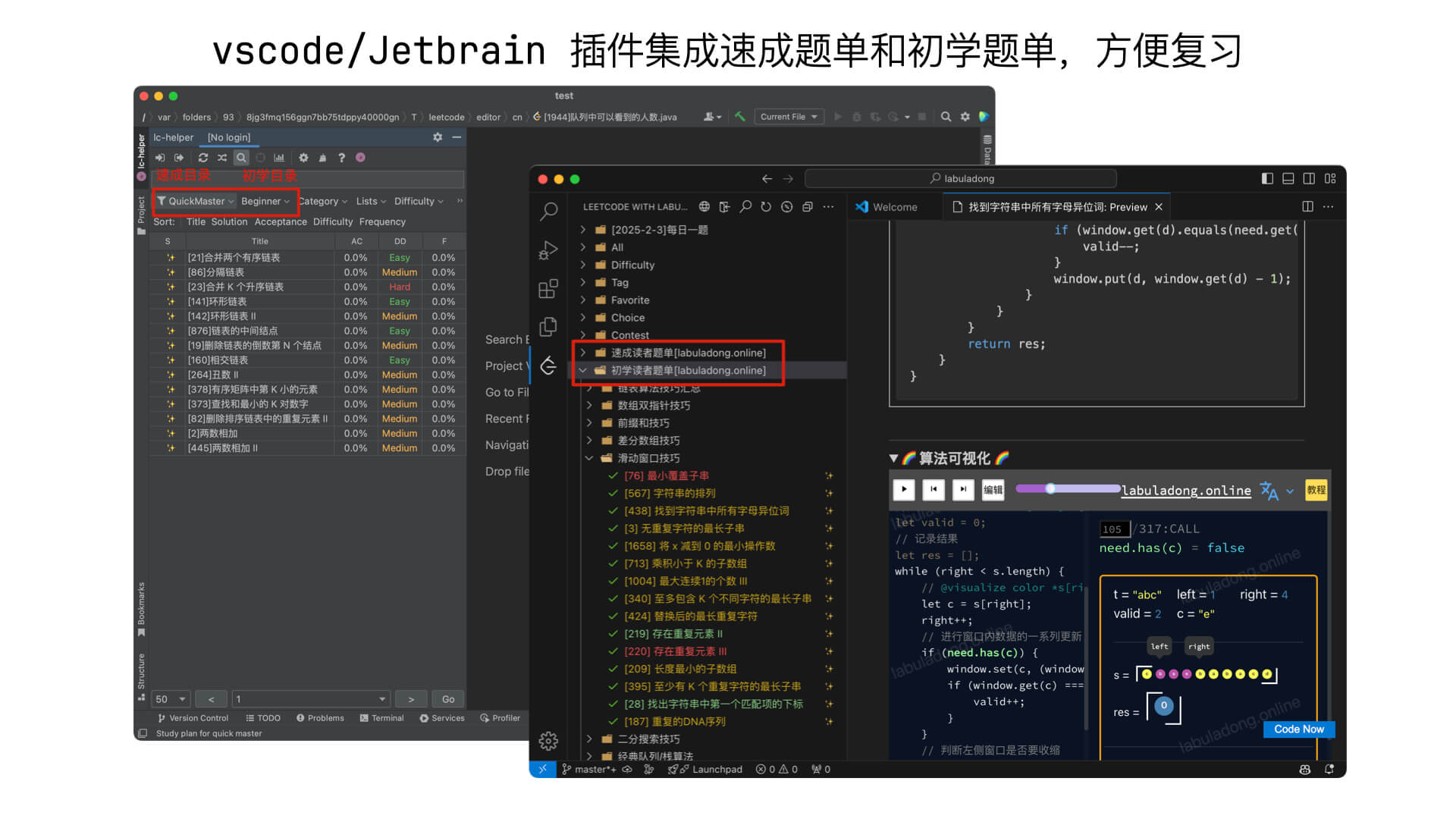
We have integrated the quick mastery plan problems into browser plugins. After installing the Chrome Extension, you can see solutions from our site when you open a LeetCode problem page. The vscode extension and Jetbrains extension also include the quick mastery problem list.
Principles of the Quick Mastery Guide
Why can this Quick Mastery Guide help you improve your algorithm skills quickly?
- Template-based solutions, unified solution style.
This guide is not just a list of problems. For each algorithm, we provide a framework template, and all exercises are solved using the same structured process. You are learning real problem-solving skills, not just memorizing answers. This means you won't be limited by the problem list. You will be able to solve new problems on your own.
- Step by step, from easy to hard, covering both data structures and algorithms.
An algorithm technique A may be a combination of technique B and C. If you don't have any background and are asked to learn A directly, it may seem very hard. But if you know B and C well, you can figure out A by yourself, and it will feel simple.
Many learners are afraid of recursion. I often say, the essence of algorithms is brute-force search, and recursion is a classic brute-force method based on tree structures. If you understand binary trees, you will understand most recursion problems. So this guide starts from key data structures, then moves to algorithm exercises. If your foundation is solid, doing exercises will be much smoother.
- Scientific study methods and rich supporting tools. We provide example problems and exercises, learning first and then practicing. With helper plugins and visual panels, we do everything we can to help you learn more easily and effectively.
Once again, I understand that some readers are pressed for time, but don't skip the framework and go straight to solving problems.
The problem with only doing exercises is that you rely too much on luck. If you get an original problem, maybe you can write the solution from memory. If not, you need your algorithm framework skills. If you haven't learned them, you'll get stuck. Building a good foundation first takes time, but in the long run, you actually save time.
Let's get started. The Guide is divided into two parts: "Data Structures" and "Algorithm Exercises." The Data Structures part does not include algorithm problems and is simpler. The Exercises part is most important, so think carefully and practice by yourself.
About Suggested Time
The suggested time for each article below is a rough estimate if you only study 1-2 hours a day in your spare time.
So the suggested time is for reference only. Actual learning speed may vary by person. If you can study for longer blocks of time, you will learn much faster.
Also, don't get stuck too long on any problem. Some things are hard to figure out by yourself at first. In the beginning, focus on understanding and following the guides on the website to build your knowledge system. When you review later, many problems will become much easier.
Data Structures
Arrays and Linked Lists
This section introduces the basic concepts of arrays and linked lists. They are simple to understand. The main point here is the circular array technique. With this technique, you can insert or delete elements at the head of the array with time complexity.
Key Foundation, Recommended Time: 1 day
Principles and Applications of Hash Tables
As a quick tutorial, we can skip the code implementation of the two ways to solve hash collisions. But it is important to understand the principles of hash tables.
Hash tables can be combined with arrays or linked lists to form more powerful data structures like LinkedHashMap and ArrayHashMap. These structures add new features to hash tables. You should know the idea behind them, so that when you see related problems, you know you have these tools.
Key Foundation, Recommended Time: 1-2 days
Binary Tree Basics and Traversal
Even though this is just the basics section, you must pay attention to binary trees, especially binary tree traversal. This is key to understanding recursion. Later, all recursive algorithms are essentially binary tree traversal in nature.
Key foundation, recommended time: 1–2 days
- Binary Tree Basics and Common Types
- Recursive and Level Order Traversal of Binary Trees
- Recursive and Level Order Traversal for N-ary Trees
- When to Use DFS and BFS
Three Level Order Traversal Patterns
First, the simplest pattern:
void levelOrderTraverse(TreeNode root) {
if (root == null) {
return;
}
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
while (!q.isEmpty()) {
TreeNode cur = q.poll();
// visit the cur node
System.out.println(cur.val);
// add the left and right children of cur to the queue
if (cur.left != null) {
q.offer(cur.left);
}
if (cur.right != null) {
q.offer(cur.right);
}
}
}void levelOrderTraverse(TreeNode* root) {
if (root == nullptr) {
return;
}
std::queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
TreeNode* cur = q.front();
q.pop();
// visit the cur node
std::cout << cur->val << std::endl;
// add the left and right children of cur to the queue
if (cur->left != nullptr) {
q.push(cur->left);
}
if (cur->right != nullptr) {
q.push(cur->right);
}
}
}from collections import deque
def levelOrderTraverse(root):
if root is None:
return
q = deque()
q.append(root)
while q:
cur = q.popleft()
# visit cur node
print(cur.val)
# add cur's left and right children to the queue
if cur.left is not None:
q.append(cur.left)
if cur.right is not None:
q.append(cur.right)func levelOrderTraverse(root *TreeNode) {
if root == nil {
return
}
q := []*TreeNode{}
q = append(q, root)
for len(q) > 0 {
cur := q[0]
q = q[1:]
// visit cur node
fmt.Println(cur.Val)
// add cur's left and right children to the queue
if cur.Left != nil {
q = append(q, cur.Left)
}
if cur.Right != nil {
q = append(q, cur.Right)
}
}
}var levelOrderTraverse = function(root) {
if (root === null) {
return;
}
var q = [];
q.push(root);
while (q.length !== 0) {
var cur = q.shift();
// visit cur node
console.log(cur.val);
// add cur's left and right children to the queue
if (cur.left !== null) {
q.push(cur.left);
}
if (cur.right !== null) {
q.push(cur.right);
}
}
}Second, a common pattern that uses step to track the level number:
void levelOrderTraverse(TreeNode root) {
if (root == null) {
return;
}
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
// record the current level being traversed (root node is considered as level 1)
int depth = 1;
while (!q.isEmpty()) {
int sz = q.size();
for (int i = 0; i < sz; i++) {
TreeNode cur = q.poll();
// visit the cur node and know its level
System.out.println("depth = " + depth + ", val = " + cur.val);
// add the left and right children of cur to the queue
if (cur.left != null) {
q.offer(cur.left);
}
if (cur.right != null) {
q.offer(cur.right);
}
}
depth++;
}
}void levelOrderTraverse(TreeNode* root) {
if (root == nullptr) {
return;
}
queue<TreeNode*> q;
q.push(root);
// record the current level being traversed (the root node is considered as level 1)
int depth = 1;
while (!q.empty()) {
int sz = q.size();
for (int i = 0; i < sz; i++) {
TreeNode* cur = q.front();
q.pop();
// visit the cur node, knowing its level
cout << "depth = " << depth << ", val = " << cur->val << endl;
// add the left and right children of cur to the queue
if (cur->left != nullptr) {
q.push(cur->left);
}
if (cur->right != nullptr) {
q.push(cur->right);
}
}
depth++;
}
}from collections import deque
def levelOrderTraverse(root):
if root is None:
return
q = deque()
q.append(root)
# record the current depth being traversed (root node is considered as level 1)
depth = 1
while q:
sz = len(q)
for i in range(sz):
cur = q.popleft()
# visit cur node and know its depth
print(f"depth = {depth}, val = {cur.val}")
# add cur's left and right children to the queue
if cur.left is not None:
q.append(cur.left)
if cur.right is not None:
q.append(cur.right)
depth += 1func levelOrderTraverse(root *TreeNode) {
if root == nil {
return
}
q := []*TreeNode{root}
// record the current depth being traversed (root node is considered as level 1)
depth := 1
for len(q) > 0 {
// get the current queue length
sz := len(q)
for i := 0; i < sz; i++ {
// dequeue the front of the queue
cur := q[0]
q = q[1:]
// visit the cur node and know its depth
fmt.Printf("depth = %d, val = %d\n", depth, cur.Val)
// add cur's left and right children to the queue
if cur.Left != nil {
q = append(q, cur.Left)
}
if cur.Right != nil {
q = append(q, cur.Right)
}
}
depth++
}
}var levelOrderTraverse = function(root) {
if (root === null) {
return;
}
let q = [];
q.push(root);
// record the current depth (root node is considered as level 1)
let depth = 1;
while (q.length !== 0) {
let sz = q.length;
for (let i = 0; i < sz; i++) {
let cur = q.shift();
// visit the cur node and know its depth
console.log("depth = " + depth + ", val = " + cur.val);
// add the left and right children of cur to the queue
if (cur.left !== null) {
q.push(cur.left);
}
if (cur.right !== null) {
q.push(cur.right);
}
}
depth++;
}
};Third, using a custom State class to keep information about each node. This is a bit more complex, but more flexible. You will see this in graph algorithms or complex BFS problems:
class State {
TreeNode node;
int depth;
State(TreeNode node, int depth) {
this.node = node;
this.depth = depth;
}
}
void levelOrderTraverse(TreeNode root) {
if (root == null) {
return;
}
Queue<State> q = new LinkedList<>();
// the path weight sum of the root node is 1
q.offer(new State(root, 1));
while (!q.isEmpty()) {
State cur = q.poll();
// visit the cur node, while knowing its path weight sum
System.out.println("depth = " + cur.depth + ", val = " + cur.node.val);
// add the left and right child nodes of cur to the queue
if (cur.node.left != null) {
q.offer(new State(cur.node.left, cur.depth + 1));
}
if (cur.node.right != null) {
q.offer(new State(cur.node.right, cur.depth + 1));
}
}
}class State {
public:
TreeNode* node;
int depth;
State(TreeNode* node, int depth) : node(node), depth(depth) {}
};
void levelOrderTraverse(TreeNode* root) {
if (root == nullptr) {
return;
}
queue<State> q;
// the path weight sum of the root node is 1
q.push(State(root, 1));
while (!q.empty()) {
State cur = q.front();
q.pop();
// visit the cur node, while knowing its path weight sum
cout << "depth = " << cur.depth << ", val = " << cur.node->val << endl;
// add the left and right children of cur to the queue
if (cur.node->left != nullptr) {
q.push(State(cur.node->left, cur.depth + 1));
}
if (cur.node->right != nullptr) {
q.push(State(cur.node->right, cur.depth + 1));
}
}
}class State:
def __init__(self, node, depth):
self.node = node
self.depth = depth
def levelOrderTraverse(root):
if root is None:
return
q = deque()
# the path weight sum of the root node is 1
q.append(State(root, 1))
while q:
cur = q.popleft()
# visit the cur node, and know its path weight sum
print(f"depth = {cur.depth}, val = {cur.node.val}")
# add the left and right child nodes of cur to the queue
if cur.node.left is not None:
q.append(State(cur.node.left, cur.depth + 1))
if cur.node.right is not None:
q.append(State(cur.node.right, cur.depth + 1))type State struct {
node *TreeNode
depth int
}
func levelOrderTraverse(root *TreeNode) {
if root == nil {
return
}
q := []State{{root, 1}}
for len(q) > 0 {
cur := q[0]
q = q[1:]
// visit the cur node, also know its path weight sum
fmt.Printf("depth = %d, val = %d\n", cur.depth, cur.node.Val)
// add cur's left and right children to the queue
if cur.node.Left != nil {
q = append(q, State{cur.node.Left, cur.depth + 1})
}
if cur.node.Right != nil {
q = append(q, State{cur.node.Right, cur.depth + 1})
}
}
}function State(node, depth) {
this.node = node;
this.depth = depth;
}
var levelOrderTraverse = function(root) {
if (root === null) {
return;
}
// @visualize bfs
var q = [];
// the path weight sum of the root node is 1
q.push(new State(root, 1));
while (q.length !== 0) {
var cur = q.shift();
// visit the cur node, while knowing its path weight sum
console.log("depth = " + cur.depth + ", val = " + cur.node.val);
// add the left and right children of cur to the queue
if (cur.node.left !== null) {
q.push(new State(cur.node.left, cur.depth + 1));
}
if (cur.node.right !== null) {
q.push(new State(cur.node.right, cur.depth + 1));
}
}
};Key foundation, recommended time: 0.5 days
A binary search tree is a special kind of binary tree. For now, just get a general idea of where it's used. You will practice problem-solving skills related to this later.
Binary Heap Principle
The key use of the binary heap is priority queues. As a quick guide, we can skip the implementation details, but you need to understand these points:
- Priority queues are data structures that can automatically keep elements sorted. Adding and removing elements have time complexity, and they are built on binary heaps.
- The binary heap is a type of complete binary tree with special properties.
- The main methods of a priority queue (binary heap) are
swimandsinkto maintain the heap property.
Key foundation, recommended time: 0.5 days
Graph Structures
Graph algorithms are a big topic. But for now, as part of the data structure basics, you just need to know how graphs are represented and implemented, and how to traverse graphs.
Actually, it's not very complicated. It is an extension of the binary tree ideas above. The following articles give templates for common graph implementations and traversal algorithms.
Key foundation, recommended time: 1 day
Start Practicing
Begin your practice now. If this is your first time using an online coding platform, you may want to check LeetCode Guide to understand the basic rules of solving problems on LeetCode.
Core Framework, Recommended Time: 0.5 Day
This article serves as the outline for all content on this site. It not only summarizes the data structures introduced above but also points out the essence of all algorithms.
There will be many links to other articles, and it may not be easy to fully understand at first read. However, there is no need to struggle; just grasp the general thinking methods introduced. As you study further content, you will gradually comprehend the essence of this article.
Linked List
The pattern of linked list problems is relatively fixed, mainly using the two-pointer technique.
Core Framework, Recommended Time: 1 Day
Exercises, Recommended Time: 1 Day
An advanced technique for singly linked lists is recursive operations, though this approach is generally mentioned during interviews. In written tests, standard pointer operations are sufficient.
Core Framework, Recommended Time: 1 Day
Arrays
Techniques related to arrays mainly involve the two-pointer approach, which can be divided into different types such as fast and slow pointers, and left and right pointers. Classic two-pointer algorithms for arrays include binary search and sliding windows.
Some readers ask why there isn't a special topic on string algorithms, as strings are essentially character arrays, and string algorithms are fundamentally array algorithms.
Core Framework, Suggested Time: 0.5 Days
Exercises, Suggested Time: 1~2 Days
Core Framework, Suggested Time: 1 Day
Sliding Window Code Template (Pseudo Code)
// Pseudocode framework of sliding window algorithm
void slidingWindow(String s) {
// Use an appropriate data structure to record the data in the
// window, which can vary according to the specific scenario
// For example, if I want to record the frequency
// of elements in the window, I would use a map
// If I want to record the sum of elements in the window, I could just use an int
Object window = ...
int left = 0, right = 0;
while (right < s.length()) {
// c is the character that will be added to the window
char c = s[right];
window.add(c)
// Expand the window
right++;
// Perform a series of updates to the data within the window
...
// *** Position of debug output ***
// Note that in the final solution code, do not use print
// Because IO operations are time-consuming and may cause timeouts
printf("window: [%d, %d)\n", left, right);
// ***********************
// Determine whether the left side of the window needs to shrink
while (left < right && window needs shrink) {
// d is the character that will be removed from the window
char d = s[left];
window.remove(d)
// Shrink the window
left++;
// Perform a series of updates to the data within the window
...
}
}
}// Pseudocode framework of sliding window algorithm
void slidingWindow(string s) {
// Use an appropriate data structure to record the data
// in the window, varying with the specific scenario
// For instance, if I want to record the frequency
// of elements in the window, I would use a map
// If I want to record the sum of elements in the window, I can simply use an int
auto window = ...
int left = 0, right = 0;
while (right < s.size()) {
// c is the character that will be entering the window
char c = s[right];
window.add(c);
// Expand the window
right++;
// Perform a series of updates to the data within the window
...
// *** position of debug output ***
printf("window: [%d, %d)\n", left, right);
// Note that printing should be avoided in the final solution code
// Because IO operations are time-consuming and may cause timeouts
// Determine whether the left side of the window needs to shrink
while (window needs shrink) {
// d is the character that will be removed from the window
char d = s[left];
window.remove(d);
// Shrink the window
left++;
// Perform a series of updates to the data within the window
...
}
}
}# Pseudocode framework for sliding window algorithm
def slidingWindow(s: str):
# Use an appropriate data structure to record the data in
# the window, which can vary depending on the scenario
# For example, if I want to record the frequency
# of elements in the window, I would use a map
# If I want to record the sum of elements in the window, I could just use an int
window = ...
left, right = 0, 0
while right < len(s):
# c is the character that will be added to the window
c = s[right]
window.add(c)
# Expand the window
right += 1
# Perform a series of updates on the data within the window
...
# *** position for debug output ***
# Note that you should not print in the final solution code
# because IO operations are time-consuming and may cause timeouts
# print(f"window: [{left}, {right})")
# ***********************
# Determine whether the left side of the window needs to be contracted
while left < right and window needs shrink:
# d is the character that will be removed from the window
d = s[left]
window.remove(d)
# Shrink the window
left += 1
# Perform a series of updates on the data within the window
...// Pseudocode framework for sliding window algorithm
func slidingWindow(s string) {
// Use an appropriate data structure to record the data in the
// window, which can vary according to the specific scenario
// For example, if I want to record the frequency of elements in the window, I use a map
// If I want to record the sum of elements in the window, I can just use an int
var window = ...
left, right := 0, 0
for right < len(s) {
// c is the character to be moved into the window
c := rune(s[right])
window[c]++
// Expand the window
right++
// Perform a series of updates to the data within the window
...
// *** debug output location ***
// Note that in the final solution code, do not print
// Because IO operations are time-consuming and may cause timeouts
fmt.Println("window: [",left,", ",right,")")
// ***********************
// Determine whether the left window needs to shrink
for left < right && window needs shrink {
// d is the character to be moved out of the window
d := rune(s[left])
window[d]--
// Shrink the window
left++
// Perform a series of updates to the data within the window
...
}
}
}// Pseudocode framework for sliding window algorithm
var slidingWindow = function(s) {
// Use an appropriate data structure to record the data in
// the window, which can vary according to the scenario
// For example, if I want to record the frequency of elements in the window, I use a map
// If I want to record the sum of the elements in the window, I can just use an int
var window = ...;
var left = 0, right = 0;
while (right < s.length) {
// c is the character that will be moved into the window
var c = s[right];
window.add(c);
// Expand the window
right++;
// Perform a series of updates on the data within the window
...
// *** debug output position ***
// Note that in the final solution code, do not print
// Because IO operations are time-consuming and may cause timeouts
console.log("window: [%d, %d)\n", left, right);
// *********************
// Determine whether the left side of the window needs to shrink
while (window needs shrink) {
// d is the character that will be moved out of the window
var d = s[left];
window.remove(d);
// Shrink the window
left++;
// Perform a series of updates on the data within the window
...
}
}
};Exercises, Suggested Time: 1 Day
Core Framework, Suggested Time: 1~2 Days
Three Binary Search Code Templates
int binary_search(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while(left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if(nums[mid] == target) {
// return directly
return mid;
}
}
// return directly
return -1;
}
int left_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// do not return, lock the left boundary
right = mid - 1;
}
}
// determine if target exists in nums
if (left < 0 || left >= nums.length) {
return -1;
}
// check if nums[left] is the target
return nums[left] == target ? left : -1;
}
int right_bound(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// do not return, lock the right boundary
left = mid + 1;
}
}
// since the while loop ends with right == left - 1
// and we are now looking for the right boundary
// it's easier to remember to use right instead of left - 1
if (right < 0 || right >= nums.length) {
return -1;
}
return nums[right] == target ? right : -1;
}int binary_search(vector<int>& nums, int target) {
int left = 0, right = nums.size()-1;
while(left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if(nums[mid] == target) {
// return directly
return mid;
}
}
// return directly
return -1;
}
int left_bound(vector<int>& nums, int target) {
int left = 0, right = nums.size()-1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// do not return, lock the left boundary
right = mid - 1;
}
}
// determine if target exists in nums
if (left < 0 || left >= nums.size()) {
return -1;
}
// check if nums[left] is target
return nums[left] == target ? left : -1;
}
int right_bound(vector<int>& nums, int target) {
int left = 0, right = nums.size()-1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// do not return, lock the right boundary
left = mid + 1;
}
}
// since the while loop ends when right == left -
// 1, and we are now finding the right boundary
// so it's easier to remember to use right instead of left - 1
if (right < 0 || right >= nums.size()) {
return -1;
}
return nums[right] == target ? right : -1;
}def binary_search(nums: List[int], target: int) -> int:
# set left and right indexes
left, right = 0, len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
right = mid - 1
elif nums[mid] == target:
# found the target value
return mid
# target value not found
return -1
def left_bound(nums: List[int], target: int) -> int:
# set left and right indexes
left, right = 0, len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
right = mid - 1
elif nums[mid] == target:
# target exists, narrow the right boundary
right = mid - 1
# determine if the target exists
if left < 0 or left >= len(nums):
return -1
# determine if the left boundary found is the target value
return left if nums[left] == target else -1
def right_bound(nums: List[int], target: int) -> int:
# set left and right indexes
left, right = 0, len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
right = mid - 1
elif nums[mid] == target:
# target exists, narrow the left boundary
left = mid + 1
# determine if the target exists
if right < 0 or right >= len(nums):
return -1
# determine if the right boundary found is the target value
return right if nums[right] == target else -1func binarySearch(nums []int, target int) int {
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right - left) / 2
if nums[mid] < target {
left = mid + 1
} else if nums[mid] > target {
right = mid - 1
} else if nums[mid] == target {
// return directly
return mid
}
}
// return directly
return -1
}
func leftBound(nums []int, target int) int {
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right - left) / 2
if nums[mid] < target {
left = mid + 1
} else if nums[mid] > target {
right = mid - 1
} else if nums[mid] == target {
// do not return, lock the left boundary
right = mid - 1
}
}
// determine if target exists in nums
if left < 0 || left >= len(nums) {
return -1
}
// determine if nums[left] is target
if nums[left] == target {
return left
}
return -1
}
func rightBound(nums []int, target int) int {
left, right := 0, len(nums)-1
for left <= right {
mid := left + (right - left) / 2
if nums[mid] < target {
left = mid + 1
} else if nums[mid] > target {
right = mid - 1
} else if nums[mid] == target {
// do not return, lock the right boundary
left = mid + 1
}
}
if right < 0 || right >= len(nums) {
return -1
}
if nums[right] == target {
return right
}
return -1
}var binary_search = function(nums, target) {
var left = 0, right = nums.length - 1;
while(left <= right) {
var mid = left + Math.floor((right - left) / 2);
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if(nums[mid] == target) {
// return directly
return mid;
}
}
// return directly
return -1;
}
var left_bound = function(nums, target) {
var left = 0, right = nums.length - 1;
while (left <= right) {
var mid = left + Math.floor((right - left) / 2);
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// do not return, lock the left boundary
right = mid - 1;
}
}
// determine if target exists in nums
if (left < 0 || left >= nums.length) {
return -1;
}
// check if nums[left] is the target
return nums[left] == target ? left : -1;
}
var right_bound = function(nums, target) {
var left = 0, right = nums.length - 1;
while (left <= right) {
var mid = left + Math.floor((right - left) / 2);
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else if (nums[mid] == target) {
// do not return, lock the right boundary
left = mid + 1;
}
}
// since the loop ends when right == left - 1 and we are looking for the right boundary
// so using right instead of left - 1 is easier to remember
if (right < 0 || right >= nums.length) {
return -1;
}
return nums[right] == target ? right : -1;
}Core Framework, Suggested Time: 1~2 Days
Prefix Sum Array Code Templates
One-Dimensional Prefix Sum:
class NumArray {
// prefix sum array
private int[] preSum;
// input an array to construct the prefix sum
public NumArray(int[] nums) {
// preSum[0] = 0, to facilitate the calculation of accumulated sums
preSum = new int[nums.length + 1];
// calculate the accumulated sums of nums
for (int i = 1; i < preSum.length; i++) {
preSum[i] = preSum[i - 1] + nums[i - 1];
}
}
// query the sum of the closed interval [left, right]
public int sumRange(int left, int right) {
return preSum[right + 1] - preSum[left];
}
}#include <vector>
class NumArray {
// prefix sum array
std::vector<int> preSum;
// input an array to construct the prefix sum
public:
NumArray(std::vector<int>& nums) {
// preSum[0] = 0, to facilitate the calculation of accumulated sums
preSum.resize(nums.size() + 1);
// calculate the accumulated sums of nums
for (int i = 1; i < preSum.size(); i++) {
preSum[i] = preSum[i - 1] + nums[i - 1];
}
}
// query the sum of the closed interval [left, right]
int sumRange(int left, int right) {
return preSum[right + 1] - preSum[left];
}
};class NumArray:
# prefix sum array
def __init__(self, nums: List[int]):
# input an array to construct the prefix sum
# preSum[0] = 0, to facilitate the calculation of accumulated sums
self.preSum = [0] * (len(nums) + 1)
# calculate the accumulated sums of nums
for i in range(1, len(self.preSum)):
self.preSum[i] = self.preSum[i - 1] + nums[i - 1]
# query the sum of the closed interval [left, right]
def sumRange(self, left: int, right: int) -> int:
return self.preSum[right + 1] - self.preSum[left]type NumArray struct {
// prefix sum array
PreSum []int
}
// input an array to construct the prefix sum
func Constructor(nums []int) NumArray {
// PreSum[0] = 0, to facilitate the calculation of accumulated sums
preSum := make([]int, len(nums)+1)
// calculate the accumulated sums of nums
for i := 1; i < len(preSum); i++ {
preSum[i] = preSum[i-1] + nums[i-1]
}
return NumArray{PreSum: preSum}
}
// query the sum of the closed interval [left, right]
func (this *NumArray) SumRange(left int, right int) int {
// The following line includes the missing comment:
// PreSum[0] = 0, to facilitate the calculation of accumulated sums
return this.PreSum[right+1] - this.PreSum[left] // Here we are using the prefix sum property, no need to repeat the comment here.
}var NumArray = function(nums) {
// prefix sum array
let preSum = new Array(nums.length + 1).fill(0);
// preSum[0] = 0, to facilitate the calculation of accumulated sums
preSum[0] = 0;
// input an array to construct the prefix sum
for (let i = 1; i < preSum.length; i++) {
// calculate the accumulated sums of nums
preSum[i] = preSum[i - 1] + nums[i - 1];
}
this.preSum = preSum;
};
// query the sum of the closed interval [left, right]
NumArray.prototype.sumRange = function(left, right) {
return this.preSum[right + 1] - this.preSum[left];
};Two-Dimensional Prefix Sum:
class NumMatrix {
// preSum[i][j] records the sum of elements in the matrix [0, 0, i-1, j-1]
private int[][] preSum;
public NumMatrix(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
if (m == 0 || n == 0) return;
// construct the prefix sum matrix
preSum = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
// calculate the sum of elements for each matrix [0, 0, i, j]
preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i - 1][j - 1] - preSum[i-1][j-1];
}
}
}
// calculate the sum of elements in the submatrix [x1, y1, x2, y2]
public int sumRegion(int x1, int y1, int x2, int y2) {
// the sum of the target matrix is obtained by operations on four adjacent matrices
return preSum[x2+1][y2+1] - preSum[x1][y2+1] - preSum[x2+1][y1] + preSum[x1][y1];
}
}#include <vector>
class NumMatrix {
// preSum[i][j] records the sum of elements in the matrix [0, 0, i-1, j-1]
std::vector<std::vector<int>> preSum;
public:
NumMatrix(std::vector<std::vector<int>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
if (m == 0 || n == 0) return;
// construct the prefix sum matrix
preSum.resize(m + 1, std::vector<int>(n + 1, 0));
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
// calculate the sum of elements for each matrix [0, 0, i, j]
preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i - 1][j - 1] - preSum[i-1][j-1];
}
}
}
// calculate the sum of elements in the submatrix [x1, y1, x2, y2]
int sumRegion(int x1, int y1, int x2, int y2) {
// the sum of the target matrix is obtained by operations on four adjacent matrices
return preSum[x2+1][y2+1] - preSum[x1][y2+1] - preSum[x2+1][y1] + preSum[x1][y1];
}
};class NumMatrix:
# preSum[i][j] records the sum of elements in the matrix [0, 0, i-1, j-1]
def __init__(self, matrix: List[List[int]]):
m = len(matrix)
n = len(matrix[0])
if m == 0 or n == 0:
return
# construct the prefix sum matrix
self.preSum = [[0] * (n + 1) for _ in range(m + 1)]
for i in range(1, m + 1):
for j in range(1, n + 1):
# calculate the sum of elements for each matrix [0, 0, i, j]
self.preSum[i][j] = (self.preSum[i - 1][j] + self.preSum[i][j - 1] +
matrix[i - 1][j - 1] - self.preSum[i - 1][j - 1])
# calculate the sum of elements in the submatrix [x1, y1, x2, y2]
def sumRegion(self, x1: int, y1: int, x2: int, y2: int) -> int:
# the sum of the target matrix is obtained by operations on four adjacent matrices
return (self.preSum[x2 + 1][y2 + 1] - self.preSum[x1][y2 + 1] -
self.preSum[x2 + 1][y1] + self.preSum[x1][y1])type NumMatrix struct {
// preSum[i][j] records the sum of elements in the matrix [0, 0, i-1, j-1]
preSum [][]int
}
func Constructor(matrix [][]int) NumMatrix {
m := len(matrix)
if m == 0 {
return NumMatrix{}
}
n := len(matrix[0])
if n == 0 {
return NumMatrix{}
}
// construct the prefix sum matrix
preSum := make([][]int, m+1)
for i := range preSum {
preSum[i] = make([]int, n+1)
}
for i := 1; i <= m; i++ {
for j := 1; j <= n; j++ {
// calculate the sum of elements for each matrix [0, 0, i, j]
preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i-1][j-1] - preSum[i-1][j-1]
}
}
return NumMatrix{preSum: preSum}
}
// calculate the sum of elements in the submatrix [x1, y1, x2, y2]
func (this *NumMatrix) SumRegion(x1, y1, x2, y2 int) int {
// the sum of the target matrix is obtained by operations on four adjacent matrices
return this.preSum[x2+1][y2+1] - this.preSum[x1][y2+1] - this.preSum[x2+1][y1] + this.preSum[x1][y1]
}var NumMatrix = function(matrix) {
let m = matrix.length, n = matrix[0].length;
// preSum[i][j] records the sum of elements in the matrix [0, 0, i-1, j-1]
this.preSum = Array.from({length: m + 1}, () => Array(n + 1).fill(0));
if (m == 0 || n == 0) return;
// construct the prefix sum matrix
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
// calculate the sum of elements for each matrix [0, 0, i, j]
this.preSum[i][j] = this.preSum[i-1][j] + this.preSum[i][j-1] + matrix[i - 1][j - 1] - this.preSum[i-1][j-1];
}
}
};
NumMatrix.prototype.sumRegion = function(x1, y1, x2, y2) {
// calculate the sum of elements in the submatrix [x1, y1, x2, y2]
// the sum of the target matrix is obtained by operations on four adjacent matrices
return this.preSum[x2+1][y2+1] - this.preSum[x1][y2+1] - this.preSum[x2+1][y1] + this.preSum[x1][y1];
};Difference Array Code Template
// Difference Array Utility Class
class Difference {
// difference array
private int[] diff;
// input an initial array, range operations will be performed on this array
public Difference(int[] nums) {
assert nums.length > 0;
diff = new int[nums.length];
// construct the difference array based on the initial array
diff[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
diff[i] = nums[i] - nums[i - 1];
}
}
// increment the closed interval [i, j] by val (can be negative)
public void increment(int i, int j, int val) {
diff[i] += val;
if (j + 1 < diff.length) {
diff[j + 1] -= val;
}
}
// return the result array
public int[] result() {
int[] res = new int[diff.length];
// construct the result array based on the difference array
res[0] = diff[0];
for (int i = 1; i < diff.length; i++) {
res[i] = res[i - 1] + diff[i];
}
return res;
}
}// Difference Array Tool Class
class Difference {
// difference array
private:
vector<int> diff;
// input an initial array, range operations will be performed on this array
public:
Difference(vector<int>& nums) {
diff = vector<int>(nums.size());
// construct the difference array based on the initial array
diff[0] = nums[0];
for (int i = 1; i < nums.size(); i++) {
diff[i] = nums[i] - nums[i - 1];
}
}
// add val (can be negative) to the closed interval [i, j]
void increment(int i, int j, int val) {
diff[i] += val;
if (j + 1 < diff.size()) {
diff[j + 1] -= val;
}
}
// return the result array
vector<int> result() {
vector<int> res(diff.size());
// construct the result array based on the difference array
res[0] = diff[0];
for (int i = 1; i < diff.size(); i++) {
res[i] = res[i - 1] + diff[i];
}
return res;
}
};# Difference Array Tool Class
class Difference:
# difference array
def __init__(self, nums: List[int]):
assert len(nums) > 0
self.diff = [0] * len(nums)
# construct the difference array based on the initial array
self.diff[0] = nums[0]
for i in range(1, len(nums)):
self.diff[i] = nums[i] - nums[i - 1]
# increment the closed interval [i, j] by val (can be negative)
def increment(self, i: int, j: int, val: int) -> None:
self.diff[i] += val
if j + 1 < len(self.diff):
self.diff[j + 1] -= val
# return the result array
def result(self) -> List[int]:
res = [0] * len(self.diff)
# construct the result array based on the difference array
res[0] = self.diff[0]
for i in range(1, len(self.diff)):
res[i] = res[i - 1] + self.diff[i]
return res// Difference array utility class
type Difference struct {
// difference array
diff []int
}
// Input an initial array, interval operations will be performed on this array
func NewDifference(nums []int) *Difference {
diff := make([]int, len(nums))
// construct the difference array based on the initial array
diff[0] = nums[0]
for i := 1; i < len(nums); i++ {
diff[i] = nums[i] - nums[i-1]
}
return &Difference{diff: diff}
}
// Add val (can be negative) to the closed interval [i, j]
func (d *Difference) Increment(i, j, val int) {
d.diff[i] += val
if j+1 < len(d.diff) {
d.diff[j+1] -= val
}
}
// Return the result array
func (d *Difference) Result() []int {
res := make([]int, len(d.diff))
// construct the result array based on the difference array
res[0] = d.diff[0]
for i := 1; i < len(d.diff); i++ {
res[i] = res[i-1] + d.diff[i]
}
return res
}class Difference {
constructor(nums) {
// difference array
this.diff = new Array(nums.length);
// construct the difference array based on the initial array
this.diff[0] = nums[0];
for (let i = 1; i < nums.length; i++) {
this.diff[i] = nums[i] - nums[i - 1];
}
}
// increase the closed interval [i, j] by val (can be negative)
increment(i, j, val) {
this.diff[i] += val;
if (j + 1 < this.diff.length) {
this.diff[j + 1] -= val;
}
}
// return the result array
result() {
let res = new Array(this.diff.length);
// construct the result array based on the difference array
res[0] = this.diff[0];
for (let i = 1; i < this.diff.length; i++) {
res[i] = res[i - 1] + this.diff[i];
}
return res;
}
}Queue/Stack
Queues and stacks are relatively simple data structures, but their application in algorithm problems requires dedicated practice.
Core Framework, Suggested Time: 0.5 Days
Exercises, Suggested Time: 1-2 Days
Monotonic stacks and queues are two variants based on stacks and queues, capable of solving specific problems that need to be mastered.
Core Framework, Suggested Time: 1-2 Days
Exercises, Suggested Time: 1-2 Days
Binary Trees & Recursive Thinking
The essence of all recursive algorithms is the traversal of binary trees. Binary tree algorithms frequently appear in interviews and tests, so I have included several articles in the binary tree section. I hope everyone will study and understand them thoroughly and practice hands-on.
Core Framework, Recommended Time: 0.5 Days
This article combines several simple classic algorithm problems to understand all recursive algorithms from the perspective of trees and classifies all recursive algorithms into two thinking patterns.
Core Framework, Recommended Time: 1 Day
This core outline is a comprehensive guide, mainly consisting of two parts: The first part is how to understand the pre-order, in-order, and post-order positions of binary trees in real algorithm problems; the second part introduces backtracking/dynamic programming algorithms from the perspective of binary trees.
Since you are already familiar with binary tree traversal algorithms, please study the first part carefully. The advanced algorithms mentioned in the second part do not require in-depth study at this moment. You just need to have an impression, which will deepen after learning backtracking/dynamic programming in the future.
Core Framework, Recommended Time: 2~3 Days
The examples in these tutorials are essential binary tree classic problems that need to be mastered.
Exercises, Recommended Time: 1 Day
Exercises, Recommended Time: 2 Days
I emphasize the importance of binary tree-related algorithm problems because the essence of algorithms is brute-force, and the tree structure is the core abstraction of all brute-force algorithms. Once you master binary trees, understanding advanced algorithms will become easier.
Our Binary Tree Algorithm Exercises Collection dedicates an entire chapter to practicing binary tree algorithms. According to the classification in Binary Tree Algorithms (Outline), the exercises are divided into three main parts:
Recursion, solving problems using the "traversal" thinking pattern.
Recursion, solving problems using the "problem decomposition" thinking pattern.
Non-recursion, solving problems using the "level-order traversal" thinking pattern.
The "traversal" thinking pattern is the prototype of DFS and backtracking algorithms explained later. The "problem decomposition" thinking pattern is the prototype of dynamic programming and divide-and-conquer algorithms. "Level-order traversal" is the prototype of BFS algorithms explained later.
Therefore, it is essential to practice these binary tree algorithms. The Binary Tree Algorithm Exercises Collection contains a substantial number of exercises. Below are exercises of moderate difficulty and high frequency of assessment for quick mastery readers:
- 【Exercise】Solving Problems with the "Traversal" Thinking I
- 【Exercise】Solving Problems with the "Problem Decomposition" Thinking I
- 【Exercise】Solving Problems with Level-Order Traversal I
If you have time and interest, you may explore other exercise sections for practice.
Binary Search Tree
A binary search tree is a special kind of binary tree. Its rule is "left child is smaller, right child is bigger". Use this feature to make tree traversal more efficient.
Core Learning, Recommended Time: 1-2 Days
Core Learning, Recommended Time: 1 Day
Data Structure Design
LRU is a classic data structure design problem that you must know. LFU is harder and can be learned optionally.
Exercises, Recommended Time: 1 Day
Exercises, Recommended Time: 1 Day
Implementing a calculator is a classic data structure design problem. If you don't have much time, you can save the calculator code at the end. If you get a string calculation problem in a test, you can just copy and use it.
Implementation of a General Calculator
class Solution {
public int calculate(String s) {
// key is the index of the left parenthesis, value is the
// corresponding index of the right parenthesis
Map<Integer, Integer> rightIndex = new HashMap<>();
// use stack structure to find the corresponding parentheses
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {
stack.push(i);
} else if (s.charAt(i) == ')') {
rightIndex.put(stack.pop(), i);
}
}
return _calculate(s, 0, s.length() - 1, rightIndex);
}
// Definition: return the result of the expression within s[start..end]
private int _calculate(String s, int start, int end, Map<Integer, Integer> rightIndex) {
// need to convert the string to a deque for easy operation
Stack<Integer> stk = new Stack<>();
// record the number in the formula
int num = 0;
// record the sign before num, initialized to +
char sign = '+';
for (int i = start; i <= end; i++) {
char c = s.charAt(i);
if (Character.isDigit(c)) {
num = 10 * num + (c - '0');
}
if (c == '(') {
// recursively calculate the expression inside the parentheses
num = _calculate(s, i + 1, rightIndex.get(i) - 1, rightIndex);
i = rightIndex.get(i);
}
if (c == '+' || c == '-' || c == '*' || c == '/' || i == end) {
int pre;
switch (sign) {
case '+':
stk.push(num);
break;
case '-':
stk.push(-num);
break;
// just take out the previous number and perform the corresponding operation
case '*':
pre = stk.pop();
stk.push(pre * num);
break;
case '/':
pre = stk.pop();
stk.push(pre / num);
break;
}
// update the sign to the current sign, reset the number to zero
sign = c;
num = 0;
}
}
// sum all results in the stack to get the answer
int res = 0;
while (!stk.isEmpty()) {
res += stk.pop();
}
return res;
}
}class Solution {
public:
int calculate(string s) {
// key is the index of the left parenthesis, value is the
// index of the corresponding right parenthesis
unordered_map<int, int> rightIndex;
// use stack structure to find the corresponding parentheses
stack<int> stack;
for (int i = 0; i < s.length(); i++) {
if (s[i] == '(') {
stack.push(i);
} else if (s[i] == ')') {
rightIndex[stack.top()] = i;
stack.pop();
}
}
return _calculate(s, 0, s.length() - 1, rightIndex);
}
private:
// definition: return the calculation result of the expression in s[start..end]
int _calculate(string s, int start, int end, unordered_map<int, int> &rightIndex) {
// need to convert the string into a deque for easy operation
stack<int> stk;
// record the number in the formula
int num = 0;
// record the sign before num, initialized to +
char sign = '+';
for (int i = start; i <= end; i++) {
char c = s[i];
if (isdigit(c)) {
num = 10 * num + (c - '0');
}
if (c == '(') {
// recursively calculate the expression in the parentheses
num = _calculate(s, i + 1, rightIndex[i] - 1, rightIndex);
i = rightIndex[i];
}
if (c == '+' || c == '-' || c == '*' || c == '/' || i == end) {
int pre;
switch (sign) {
case '+':
stk.push(num);
break;
case '-':
stk.push(-num);
break;
// just take out the previous number and perform the corresponding operation
case '*':
pre = stk.top(); stk.pop();
stk.push(pre * num);
break;
case '/':
pre = stk.top(); stk.pop();
stk.push(pre / num);
break;
}
// update the sign to the current sign, reset the number to zero
sign = c;
num = 0;
}
}
// summing all the results in the stack gives the answer
int res = 0;
while (!stk.empty()) {
res += stk.top();
stk.pop();
}
return res;
}
};class Solution:
def calculate(self, s: str) -> int:
# key is the index of the left parenthesis, value is the
# corresponding index of the right parenthesis
rightIndex = {}
# use stack structure to find the corresponding parenthesis
stack = []
for i in range(len(s)):
if s[i] == '(':
stack.append(i)
elif s[i] == ')':
rightIndex[stack.pop()] = i
return self._calculate(s, 0, len(s) - 1, rightIndex)
# Definition: return the calculation result of the expression within s[start..end]
def _calculate(self, s, start, end, rightIndex):
# need to convert the string to a deque for easy operation
stk = []
# record the number in the formula
num = 0
# record the sign before num, initialized to +
sign = '+'
i = start
while i <= end:
c = s[i]
if c.isdigit():
num = 10 * num + int(c)
if c == '(':
# recursively calculate the expression inside the parenthesis
num = self._calculate(s, i + 1, rightIndex[i] - 1, rightIndex)
i = rightIndex[i]
if c in '+-*/' or i == end:
if sign == '+':
stk.append(num)
elif sign == '-':
stk.append(-num)
elif sign == '*':
pre = stk.pop()
stk.append(pre * num)
elif sign == '/':
pre = stk.pop()
stk.append(int(pre / num))
# update the sign to the current sign, reset the number to zero
sign = c
num = 0
i += 1
# sum all results in the stack to get the answer
res = 0
while stk:
res += stk.pop()
return resfunc calculate(s string) int {
// key is the index of the left parenthesis, value is
// the corresponding index of the right parenthesis
rightIndex := make(map[int]int)
// use stack structure to find the corresponding parentheses
stack := []int{}
for i := 0; i < len(s); i++ {
if s[i] == '(' {
stack = append(stack, i)
} else if s[i] == ')' {
pop := stack[len(stack)-1]
stack = stack[:len(stack)-1]
rightIndex[pop] = i
}
}
return _calculate(s, 0, len(s)-1, rightIndex)
}
// definition: return the result of the expression within s[start..end]
func _calculate(s string, start int, end int, rightIndex map[int]int) int {
// need to convert the string into a deque for easy operations
stk := []int{}
// record the number in the expression
num := 0
// record the sign before num, initialize to +
// change to byte type
sign := byte('+')
for i := start; i <= end; i++ {
c := s[i]
if c >= '0' && c <= '9' {
num = 10*num + int(c-'0')
}
if c == '(' {
// recursively calculate the expression inside the parentheses
num = _calculate(s, i+1, rightIndex[i]-1, rightIndex)
i = rightIndex[i]
}
if c == '+' || c == '-' || c == '*' || c == '/' || i == end {
var pre int
switch sign {
case '+':
stk = append(stk, num)
case '-':
stk = append(stk, -num)
// just take out the previous number to do the corresponding operation
case '*':
pre = stk[len(stk)-1]
stk[len(stk)-1] = pre * num
case '/':
pre = stk[len(stk)-1]
stk[len(stk)-1] = pre / num
}
// update the sign to the current sign, reset the number to zero
sign = c
num = 0
}
}
// summing all the results in the stack is the answer
res := 0
for len(stk) != 0 {
res += stk[len(stk)-1]
stk = stk[:len(stk)-1]
}
return res
}var calculate = function(s) {
// key is the index of the left parenthesis, value is
// the index of the corresponding right parenthesis
let rightIndex = new Map();
// use stack structure to find corresponding parentheses
let stack = [];
for (let i = 0; i < s.length; i++) {
if (s[i] === '(') {
stack.push(i);
} else if (s[i] === ')') {
rightIndex.set(stack.pop(), i);
}
}
return _calculate(s, 0, s.length - 1, rightIndex);
};
var _calculate = function(s, start, end, rightIndex) {
// need to convert the string to a deque for easy manipulation
let stk = [];
// record the number in the formula
let num = 0;
// record the sign before num, initialize as +
let sign = '+';
for (let i = start; i <= end; i++) {
let c = s[i];
if (/\d/.test(c)) {
num = 10 * num + (c - '0');
}
if (c === '(') {
// recursively calculate the expression inside the parentheses
num = _calculate(s, i + 1, rightIndex.get(i) - 1, rightIndex);
i = rightIndex.get(i);
}
if ('+-*/'.includes(c) || i === end) {
let pre;
switch (sign) {
case '+':
stk.push(num);
break;
case '-':
stk.push(-num);
break;
// just take out the previous number for corresponding operation
case '*':
pre = stk.pop();
stk.push(pre * num);
break;
case '/':
pre = stk.pop();
// correct integer division
stk.push(Math.trunc(pre / num));
break;
}
// update the sign to the current sign, reset number to zero
sign = c;
num = 0;
}
}
// summing up all the results in the stack is the answer
let res = 0;
while (stk.length) {
res += stk.pop();
}
return res;
};Exercises, Recommended Time: 1 Day
Graph Algorithms
Cycle detection, topological sort, and bipartite graph check are classic graph algorithms. They are mainly about graph traversal and are easy to learn.
Core Framework, recommended time 1~2 days
The Union Find algorithm is a useful graph algorithm. You need to know its basic idea and API.
It is recommended to save the UF class given below. If the coding platform allows, you can reuse it directly.
Core Framework, recommended time 1 day
Union Find Code Template
Here is the most efficient path compression implementation:
class UF {
// the number of connected components
private int count;
// store the parent of each node
private int[] parent;
// n is the number of nodes in the graph
public UF(int n) {
this.count = n;
parent = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
// connect node p and node q
public void union(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
parent[rootQ] = rootP;
// merge two connected components into one
count--;
}
// determine if node p and node q are connected
public boolean connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
public int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
// return the number of connected components in the graph
public int count() {
return count;
}
}class UF {
private:
// the number of connected components
int _count;
// store the parent of each node
vector<int> parent;
public:
// n is the number of nodes in the graph
UF(int n) {
this->_count = n;
this->parent.resize(n);
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
// connect node p and node q
void union_(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ)
return;
parent[rootQ] = rootP;
// merge two connected components into one
_count--;
}
// determine if node p and node q are connected
bool connected(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
return rootP == rootQ;
}
int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
// return the number of connected components in the graph
int count() {
return _count;
}
};class UF:
# the number of connected components
_count: int
# store the parent of each node
parent: List[int]
# n is the number of nodes in the graph
def __init__(self, n: int):
self._count = n
self.parent = [i for i in range(n)]
# connect node p and node q
def union(self, p: int, q: int):
rootP = self.find(p)
rootQ = self.find(q)
if rootP == rootQ:
return
self.parent[rootQ] = rootP
# merge two connected components into one
self._count -= 1
# determine if node p and node q are connected
def connected(self, p: int, q: int) -> bool:
rootP = self.find(p)
rootQ = self.find(q)
return rootP == rootQ
def find(self, x: int) -> int:
if self.parent[x] != x:
self.parent[x] = self.find(self.parent[x])
return self.parent[x]
# return the number of connected components in the graph
def count(self) -> int:
return self._counttype UF struct {
// the number of connected components
count int
// store the parent of each node
parent []int
}
// n is the number of nodes in the graph
func NewUF(n int) *UF {
parent := make([]int, n)
for i := 0; i < n; i++ {
parent[i] = i
}
return &UF{
count: n,
parent: parent,
}
}
// connect node p and node q
func (u *UF) Union(p, q int) {
rootP := u.Find(p)
rootQ := u.Find(q)
if rootP == rootQ {
return
}
u.parent[rootQ] = rootP
// merge two connected components into one
u.count--
}
// determine if node p and node q are connected
func (u *UF) Connected(p, q int) bool {
rootP := u.Find(p)
rootQ := u.Find(q)
return rootP == rootQ
}
func (u *UF) Find(x int) int {
if u.parent[x] != x {
u.parent[x] = u.Find(u.parent[x])
}
return u.parent[x]
}
// return the number of connected components in the graph
func (u *UF) Count() int {
return u.count
}class UF {
// n is the number of nodes in the graph
constructor(n) {
// number of connected components
this._count = n
// store the parent of each node
this.parent = Array.from({ length: n }, (_, index) => index)
}
// connect node p and node q
union(p, q) {
const rootP = this.find(p)
const rootQ = this.find(q)
if (rootP === rootQ) {
return
}
this.parent[rootQ] = rootP
// merge two connected components into one
this._count--
}
// determine if node p and node q are connected
connected(p, q) {
const rootP = this.find(p)
const rootQ = this.find(q)
return rootP === rootQ
}
find(x) {
if (this.parent[x] !== x) {
this.parent[x] = this.find(this.parent[x])
}
return this.parent[x]
}
// return the number of connected components in the graph
count() {
return this._count
}
}Minimum Spanning Tree is another useful graph algorithm. You need to know its definition and typical use cases.
Kruskal and Prim are two classic Minimum Spanning Tree algorithms. Kruskal is basically Union Find plus sorting, and is simpler, so for quick learning, you can focus on Kruskal.
Core Framework, recommended time 1 day
Dijkstra's shortest path algorithm is also a classic and you should know it. It is an improved version of binary tree BFS. Save the template to use quickly in coding.
Core Framework, recommended time 1 day
Dijkstra Algorithm Template (Pseudocode)
class State {
// Current node ID
int node;
// Minimum path weight from the start node s to the current node
int distFromStart;
public State(int node, int distFromStart) {
this.node = node;
this.distFromStart = distFromStart;
}
}
// Input the weighted graph (without negative weight edges) graph and the starting node src
// Return the minimum path weight from the starting node src to other nodes
int[] dijkstra(Graph graph, int src) {
// Record the minimum path weight from the starting node src to other nodes
// distTo[i] represents the minimum path weight from the starting node src to node i
int[] distTo = new int[graph.size()];
// Initialize all values to positive infinity, representing not calculated
Arrays.fill(distTo, Integer.MAX_VALUE);
// Priority queue, nodes with smaller distFromStart are in front
Queue<State> pq = new PriorityQueue<>((a, b) -> {
return a.distFromStart - b.distFromStart;
});
// Start BFS from the starting node src
pq.offer(new State(src, 0));
distTo[src] = 0;
while (!pq.isEmpty()) {
State state = pq.poll();
int curNode = state.node;
int curDistFromStart = state.distFromStart;
if (distTo[curNode] < curDistFromStart) {
// In Dijkstra's algorithm, the queue may contain duplicate nodes state
// So it is necessary to check when the element leaves the
// queue to remove the worse duplicate nodes
continue;
}
for (Edge e : graph.neighbors(curNode)) {
int nextNode = e.to;
int nextDistFromStart = curDistFromStart + e.weight;
if (distTo[nextNode] <= nextDistFromStart) {
continue;
}
// Add nextNode node to the priority queue
pq.offer(new State(nextNode, nextDistFromStart));
// Record the minimum path weight from the starting node to the nextNode node
distTo[nextNode] = nextDistFromStart;
}
}
return distTo;
}// State stored in the priority queue
struct State {
// Current node ID
int node;
// Minimum path weight from start node s to the current node
int distFromStart;
State(int _node, int _distFromStart)
: node(_node), distFromStart(_distFromStart) {}
};
// Custom comparator so that State with smaller distFromStart dequeues first
struct Compare {
bool operator()(const State& a, const State& b) const {
return a.distFromStart > b.distFromStart;
}
};
// Input the weighted graph (without negative weight edges) graph and the starting node src
// Return the minimum path weight from the starting node src to other nodes
std::vector<int> dijkstra(Graph& graph, int src) {
// Record the minimum path weight from the starting node src to other nodes
// distTo[i] represents the minimum path weight from the starting node src to node i
std::vector<int> distTo(graph.size(), INT_MAX);
// Priority queue, nodes with smaller distFromStart are in front
std::priority_queue<State, std::vector<State>, Compare> pq;
// Start BFS from the starting node src
pq.emplace(src, 0);
distTo[src] = 0;
while (!pq.empty()) {
State state = pq.top();
pq.pop();
int curNode = state.node;
int curDistFromStart = state.distFromStart;
if (distTo[curNode] < curDistFromStart) {
// In Dijkstra's algorithm, the queue may contain duplicate nodes state
// So it is necessary to check when the element leaves the
// queue to remove the worse duplicate nodes
continue;
}
for (const Edge& e : graph.neighbors(curNode)) {
int nextNode = e.to;
int nextDistFromStart = curDistFromStart + e.weight;
if (distTo[nextNode] <= nextDistFromStart) {
continue;
}
// Add nextNode to the priority queue
pq.emplace(nextNode, nextDistFromStart);
// Record the minimum path weight from the starting node to the nextNode node
distTo[nextNode] = nextDistFromStart;
}
}
return distTo;
}import heapq
from typing import List
class State:
# Current node ID
def __init__(self, node: int, distFromStart: int):
self.node = node
# Minimum path weight from the start node s to the current node
self.distFromStart = distFromStart
# Define comparison for min-heap
def __lt__(self, other: "State") -> bool:
return self.distFromStart < other.distFromStart
# Input the weighted graph (without negative weight edges) graph and the starting node src
# Return the minimum path weight from the starting node src to other nodes
def dijkstra(graph: Graph, src: int) -> List[int]:
# Record the minimum path weight from the starting node src to other nodes
# distTo[i] represents the minimum path weight from the starting node src to node i
distTo: List[int] = [float('inf')] * graph.size()
# Priority queue, nodes with smaller distFromStart are in front
pq: List[State] = []
# Start BFS from the starting node src
heapq.heappush(pq, State(src, 0))
distTo[src] = 0
while pq:
state = heapq.heappop(pq)
curNode = state.node
curDistFromStart = state.distFromStart
if distTo[curNode] < curDistFromStart:
# In Dijkstra's algorithm, the queue may contain duplicate nodes state
# So it is necessary to check when the element leaves the
# queue to remove the worse duplicate nodes
continue
for e in graph.neighbors(curNode):
nextNode = e.to
nextDistFromStart = curDistFromStart + e.weight
if distTo[nextNode] <= nextDistFromStart:
continue
# Add nextNode node to the priority queue
heapq.heappush(pq, State(nextNode, nextDistFromStart))
# Record the minimum path weight from the starting node to the nextNode node
distTo[nextNode] = nextDistFromStart
package main
import (
"container/heap"
"math"
)
// State stored in the priority queue
type State struct {
// Current node ID
node int
// Minimum path weight from the start node s to the current node
distFromStart int
}
// Priority queue, nodes with smaller distFromStart are in front
type PriorityQueue []*State
func (pq PriorityQueue) Len() int { return len(pq) }
func (pq PriorityQueue) Less(i, j int) bool {
return pq[i].distFromStart < pq[j].distFromStart
}
func (pq PriorityQueue) Swap(i, j int) { pq[i], pq[j] = pq[j], pq[i] }
func (pq *PriorityQueue) Push(x interface{}) {
*pq = append(*pq, x.(*State))
}
func (pq *PriorityQueue) Pop() interface{} {
old := *pq
n := len(old)
item := old[n-1]
*pq = old[:n-1]
return item
}
// Input the weighted graph (without negative weight edges) graph and the starting node src
// Return the minimum path weight from the starting node src to other nodes
func dijkstra(graph Graph, src int) []int {
// Record the minimum path weight from the starting node src to other nodes
// distTo[i] represents the minimum path weight from the starting node src to node i
distTo := make([]int, graph.Size())
// Initialize all values to positive infinity, representing not calculated
for i := range distTo {
distTo[i] = math.MaxInt32
}
pq := &PriorityQueue{}
heap.Init(pq)
// Start BFS from the starting node src
heap.Push(pq, &State{node: src, distFromStart: 0})
distTo[src] = 0
for pq.Len() > 0 {
state := heap.Pop(pq).(*State)
curNode := state.node
curDistFromStart := state.distFromStart
if distTo[curNode] < curDistFromStart {
// In Dijkstra's algorithm, the queue may contain duplicate nodes state
// So it is necessary to check when the element
// leaves the queue to remove the worse duplicate nodes
continue
}
for _, e := range graph.neighbors(curNode) {
nextNode := e.to
nextDistFromStart := curDistFromStart + e.weight
if distTo[nextNode] <= nextDistFromStart {
continue
}
// Add nextNode node to the priority queue
heap.Push(pq, &State{node: nextNode, distFromStart: nextDistFromStart})
// Record the minimum path weight from the starting node to the nextNode node
distTo[nextNode] = nextDistFromStart
}
}
return distTo
}// State stored in the priority queue
class State {
// Current node ID
constructor(node, distFromStart) {
this.node = node;
// Minimum path weight from the start node s to the current node
this.distFromStart = distFromStart;
}
}
// Input the weighted graph (without negative weight edges) graph and the starting node src
// Return the minimum path weight from the starting node src to other nodes
function dijkstra(graph, src) {
// Record the minimum path weight from the starting node src to other nodes
// distTo[i] represents the minimum path weight from the starting node src to node i
const distTo = Array(graph.size()).fill(Infinity);
// Priority queue, nodes with smaller distFromStart are in front
const pq = new PriorityQueue((a, b) => a.distFromStart - b.distFromStart);
// Start BFS from the starting node src
pq.enqueue(new State(src, 0));
distTo[src] = 0;
while (!pq.isEmpty()) {
const state = pq.dequeue();
const curNode = state.node;
const curDistFromStart = state.distFromStart;
if (distTo[curNode] < curDistFromStart) {
// In Dijkstra's algorithm, the queue may contain duplicate nodes state
// So it is necessary to check when the element leaves the
// queue to remove the worse duplicate nodes
continue;
}
for (const e of graph.neighbors(curNode)) {
const nextNode = e.to;
const nextDistFromStart = curDistFromStart + e.weight;
if (distTo[nextNode] <= nextDistFromStart) {
continue;
}
// Add nextNode node to the priority queue
pq.enqueue(new State(nextNode, nextDistFromStart));
// Record the minimum path weight from the starting node to the nextNode node
distTo[nextNode] = nextDistFromStart;
}
}
return distTo;
}DFS/Backtracking Algorithm
Backtracking is a type of brute-force algorithm. You must know it well.
In written tests, scores are based on the number of test cases you pass. If you cannot write the best solution for some questions, you can use backtracking to try all possibilities. Even if you can't pass all the cases, you can still get some points.
The examples listed below are classic backtracking problems. You should master them fully.
Core Framework, Suggested Time: 1~2 Days
Core Framework, Suggested Time: 1~2 Days
Core Framework, Suggested Time: 1 Day
This article is about DFS:
DFS and backtracking are a bit different. This article explains the difference and gives some coding tips:
Exercises, Suggested Time: 2 Days
Most backtracking problems are about permutation and combination. If you fully understand Solve All Permutations/Combinations/Subsets Problems Quickly, you can solve many backtracking problems directly.
The backtracking exercises on this site are:
- Exercise: Classic Backtracking Problems I
- Exercise: Classic Backtracking Problems II
- Exercise: Classic Backtracking Problems III
There are many exercises. If you have time, try to do them all. If you are short on time, I will select some key problems for you. I suggest installing the Chrome Extension to see hints and code on the problem pages.
BFS Algorithm
BFS is also a brute-force algorithm and is very important to learn. It is basically the same as level-order traversal of a binary tree and is good for finding the shortest path problems.
Main Framework, Suggested Time: 1 Day
Exercises, Suggested Time: 2 Days
The BFS exercises on this site are:
These two chapters have many problems. If you have time, try to finish all. If you are in a hurry, I will pick a few for you to practice. It is recommended to install the Chrome Extension, so you can see hints and code solutions for each problem:
Dynamic Programming
Dynamic programming is also a brute-force method, but in some problems there are overlapping subproblems. So, we use memoization to optimize it. For this kind of algorithms, we call them dynamic programming.
The brute-force solution for dynamic programming is usually a recursive method. The way to optimize is always the same: either add a memo table, or change the recursion to iteration.
The hardest part in dynamic programming is how to write the brute-force solution (the state transition formula). Please read the following articles. Pay special attention to the thinking process of finding the state transition equation.
Main Framework, Suggested Time: 1-2 Days
Main Framework, Suggested Time: 1-2 Days
Exercises, Suggested Time: 1-2 Days
Exercises, Suggested Time: 1-2 Days
Greedy Algorithm
Usually, you need to try all possible solutions by brute-force and pick the best one.
But for some problems, if you use the given information well, you can find the best answer without brute-force search. This is called the greedy property, and the method is called the greedy algorithm.
Greedy algorithms do not have a fixed template. The key is to observe if you can use the information to rule out some choices that cannot be the best answer.
Core Tutorial, recommended time: 1 day
Divide and Conquer Algorithm
For some problems, using divide and conquer can be more efficient. The following tutorial uses a linked list problem as an example.
Core Tutorial, recommended time: 1 day
Math
Math-related algorithm questions are not very common in coding tests, but some classic tricks are useful to know.
Exercises, recommended time: 1-2 days
Exercises, recommended time: 1 day
Other Classic Interview Questions
Here are some classic algorithm problems that essentially apply the algorithms introduced above. After mastering all the algorithms mentioned, you should be able to tackle generally difficult interview questions.
Exercises, Recommended Time: 1-2 Days
Exercises, Recommended Time: 1-2 Days
nSum Universal Function
// Note: you must sort the nums array before calling this function
// n is the sum of how many numbers you want to find, start is the index to start
// calculation (usually fill in 0), target is the target sum you want to achieve
List<List<Integer>> nSumTarget(int[] nums, int n, int start, long target) {
int sz = nums.length;
List<List<Integer>> res = new ArrayList<>();
// at least it should be 2Sum, and the array size should not be less than n
if (n < 2 || sz < n) return res;
// 2Sum is the base case
if (n == 2) {
// the operation with two pointers
int lo = start, hi = sz - 1;
while (lo < hi) {
int sum = nums[lo] + nums[hi];
int left = nums[lo], right = nums[hi];
if (sum < target) {
while (lo < hi && nums[lo] == left) lo++;
} else if (sum > target) {
while (lo < hi && nums[hi] == right) hi--;
} else {
res.add(new ArrayList<>(Arrays.asList(left, right)));
while (lo < hi && nums[lo] == left) lo++;
while (lo < hi && nums[hi] == right) hi--;
}
}
} else {
// when n > 2, recursively calculate the result of (n-1)Sum
for (int i = start; i < sz; i++) {
List<List<Integer>> sub = nSumTarget(nums, n - 1, i + 1, target - nums[i]);
for (List<Integer> arr : sub) {
// (n-1)Sum plus nums[i] is nSum
arr.add(nums[i]);
res.add(arr);
}
while (i < sz - 1 && nums[i] == nums[i + 1]) i++;
}
}
return res;
}// Note: you must sort the nums array before calling this function
// n is the sum of how many numbers you want, start is the index to start
// calculation (usually fill 0), target is the target sum you want to make
vector<vector<int>> nSumTarget(vector<int>& nums, int n, int start, long target) {
int sz = nums.size();
vector<vector<int>> res;
// at least it's a 2Sum and the array size should not be less than n
if (n < 2 || sz < n) return res;
// 2Sum is the base case
if (n == 2) {
// the operation with two pointers
int lo = start, hi = sz - 1;
while (lo < hi) {
int sum = nums[lo] + nums[hi];
int left = nums[lo], right = nums[hi];
if (sum < target) {
while (lo < hi && nums[lo] == left) lo++;
} else if (sum > target) {
while (lo < hi && nums[hi] == right) hi--;
} else {
res.push_back({left, right});
while (lo < hi && nums[lo] == left) lo++;
while (lo < hi && nums[hi] == right) hi--;
}
}
} else {
// when n > 2, recursively calculate the result of (n-1)Sum
for (int i = start; i < sz; i++) {
vector<vector<int>> sub = nSumTarget(nums, n - 1, i + 1, target - nums[i]);
for (vector<int>& arr : sub) {
// (n-1)Sum plus nums[i] is nSum
arr.push_back(nums[i]);
res.push_back(arr);
}
while (i < sz - 1 && nums[i] == nums[i + 1]) i++;
}
}
return res;
}# Note: make sure to sort the nums array before calling this function
# n is the sum of how many numbers you want, start is the index to start
# calculation (usually fill 0), target is the target sum you want to make
def nSumTarget(nums: List[int], n: int, start: int, target: int) -> List[List[int]]:
sz = len(nums)
res = []
# at least it should be 2Sum, and the array size should not be less than n
if n < 2 or sz < n:
return res
# 2Sum is the base case
if n == 2:
# the operation with two pointers
lo, hi = start, sz-1
while lo < hi:
sum = nums[lo] + nums[hi]
left, right = nums[lo], nums[hi]
if sum < target:
while lo < hi and nums[lo] == left:
lo += 1
elif sum > target:
while lo < hi and nums[hi] == right:
hi -= 1
else:
res.append([left, right])
while lo < hi and nums[lo] == left:
lo += 1
while lo < hi and nums[hi] == right:
hi -= 1
return res
else:
# when n > 2, recursively calculate the result of (n-1)Sum
for i in range(start, sz):
if i > start and nums[i] == nums[i - 1]:
# skip duplicate elements
continue
subs = nSumTarget(nums, n-1, i+1, target-nums[i])
for sub in subs:
# (n-1)Sum plus nums[i] is nSum
sub.append(nums[i])
res.append(sub)
return res// Note: you must sort the nums array before calling this function
// n is the sum of how many numbers you want, start is the index to start
// calculation (usually fill in 0), target is the target sum you want to make
func nSumTarget(nums []int, n int, start int, target int64) [][]int {
sz := len(nums)
res := [][]int{}
// at least it's a 2Sum and the array size should not be less than n
if n < 2 || sz < n {
return res
}
// 2Sum is the base case
if n == 2 {
// the twin pointers operation
lo, hi := start, sz-1
for lo < hi {
sum := nums[lo] + nums[hi]
left, right := nums[lo], nums[hi]
if int64(sum) < target {
for lo < hi && nums[lo] == left {
lo++
}
} else if int64(sum) > target {
for lo < hi && nums[hi] == right {
hi--
}
} else {
res = append(res, []int{left, right})
for lo < hi && nums[lo] == left {
lo++
}
for lo < hi && nums[hi] == right {
hi--
}
}
}
} else {
// when n > 2, recursively calculate the result of (n-1)Sum
for i := start; i < sz; i++ {
subs := nSumTarget(nums, n-1, i+1, target-int64(nums[i]))
for _, sub := range subs {
// (n-1)Sum plus nums[i] is nSum
sub = append(sub, nums[i])
res = append(res, sub)
}
for i < sz-1 && nums[i] == nums[i+1] {
i++
}
}
}
return res
}// note: make sure to sort the array nums before calling this function
// n is the sum of how many numbers you want, start is the index to start
// calculation (usually fill 0), target is the target sum you want to make
var nSumTarget = function(nums, n, start, target) {
let sz = nums.length;
let res = [];
// at least it should be 2Sum, and the size of the array should not be less than n
if (n < 2 || sz < n) return res;
// 2Sum is the base case
if (n == 2) {
// the twin-pointer operation
let lo = start, hi = sz - 1;
while (lo < hi) {
let sum = nums[lo] + nums[hi];
let left = nums[lo], right = nums[hi];
if (sum < target) {
while (lo < hi && nums[lo] == left) lo++;
} else if (sum > target) {
while (lo < hi && nums[hi] == right) hi--;
} else {
res.push([left, right]);
while (lo < hi && nums[lo] == left) lo++;
while (lo < hi && nums[hi] == right) hi--;
}
}
// when n > 2, recursively calculate the result of (n-1)Sum
} else {
for (let i = start; i < sz; i++) {
let sub = nSumTarget(nums, n - 1, i + 1, target - nums[i]);
for (let arr of sub) {
// (n-1)Sum plus nums[i] is nSum
arr.push(nums[i]);
res.push(arr);
}
while (i < sz - 1 && nums[i] == nums[i + 1]) i++;
}
}
return res;
}Sorting Algorithms
In written tests and interviews, you are generally not asked to write sorting algorithm code; however, you might be asked about the principles, time complexity, and applicable scenarios of classic sorting algorithms, so you need to be familiar with the ten classic sorting algorithms.
Sorting Algorithms Overview, Recommended Time: 1 Day
It is recommended to watch the video in Introduction to Ten Sorting Algorithms to understand the core principles, complexity analysis, and applicable scenarios of the ten sorting algorithms.