How to Efficiently Solve the Trapping Rain Water Problem

LeetCode problem #42 "Trapping Rain Water" is quite interesting and frequently appears in interviews. This article will walk you through step-by-step optimizations to solve this problem.

First, let's look at the problem:

42. Trapping Rain Water | LeetCode |

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it can trap after raining.

Example 1:

Input: height = [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6
Explanation: The above elevation map (black section) is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped.

Example 2:

Input: height = [4,2,0,3,2,5]
Output: 9

Constraints:

• n == height.length
• 1 <= n <= 2 * 104
• 0 <= height[i] <= 105

The problem involves using an array to represent a bar chart and asks how much water this bar chart can trap at most.

int trap(int[] height);

int trap(vector<int>& height);

def trap(height: List[int]) -> int:

func trap(height []int) int {}

 var trap = function(height) {}

Let's delve into the progression from a brute-force solution to a memoization solution and finally a two-pointer solution, solving this problem in O(N) time and O(1) space.

1. Core Idea

For instance, in this problem, instead of considering how much water the entire histogram can hold, focus only on how much water can be held at position i.

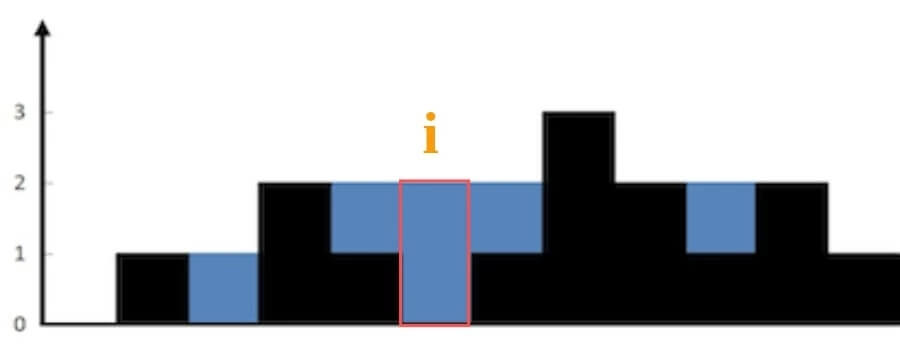
Position i can hold 2 units of water because height[i] is 0, and it can accommodate up to 2 units of water, calculated as 2-0=2.

Why can position i hold up to 2 units of water? Because the height of the water column at position i depends on the highest columns to its left and right, which we refer to as l_max and r_max, respectively. The maximum height of the water column at position i is min(l_max, r_max).

Therefore, for position i, the amount of water that can be held is: