Interesting Probability Problems

In the previous article Discussing Random Algorithms in Games, we talked about the Monte Carlo method for verifying probability algorithms. Today, let's dive into some lighter content: a few interesting problems related to probability.

There are two simplest principles for calculating probability:

Principle One: To calculate probability, you must have a reference frame called the "sample space," which includes all possible outcomes of a random event. The probability of event A occurring = Number of sample points in A / Total number of sample points in the sample space.

Principle Two: When calculating probability, it's crucial to understand that probability is a continuous whole. You cannot split continuous probability, which is known as conditional probability.

We learned these two principles in high school, but we still easily make mistakes. Interestingly, the process of making these mistakes often follows a similar pattern:

First, we overlook Principle Two and incorrectly calculate the sample space. Then, using Principle One, we arrive at the wrong answer.

Next, let's explore a few simple yet deceptive problems: the Boy or Girl problem, the Birthday Paradox, and the Monty Hall problem. Of course, the Monty Hall problem is probably the most familiar to everyone, so we'll delve into some interesting thoughts about it.

I. The Boy-Girl Problem

Imagine a family with two children. You are told that one of the children is a boy. What is the probability that the other child is also a boy?

Many people, including myself, might instinctively answer: 1/2, because the other child could either be a boy or a girl, with equal probability. However, the correct answer is actually 1/3.

Why is the initial thought wrong? It's because the sample space was not correctly calculated, leading to a mistake in the principle of probability calculation. With two children, the sample space consists of 4 possibilities: older brother and younger sister, older brother and younger brother, older sister and younger sister, and older sister and younger brother. Knowing that one child is a boy eliminates the older sister and younger sister scenario, reducing the sample space to 3. Only one of these scenarios involves both children being boys (older brother and younger brother), so the probability is 1/3.

Why does the calculation of the sample space often go wrong? It's because we overlook conditional probability, confusing the following two questions:

1. If a family has only one child, what is the probability that the child is a boy?
2. If a family has two children, and one of them is a boy, what is the probability that the other child is also a boy?

According to the second principle, probability problems are continuous, and these two questions should not be confused. The second question requires the use of conditional probability, which is the probability of one child being a boy given that the other child is a boy. Applying the formula for conditional probability makes this calculation straightforward.

Through this problem, readers should understand the relationship between the two principles of probability calculation. The most misleading aspect is the neglect of conditional probability. To avoid being misled, the simplest method is to enumerate all possible outcomes.

Finally, I've encountered a rather odd objection to this problem: What if the two children are twins and there is no age difference between them?

I must admit, there seems to be a hint of logic in this! However, we use age difference to represent the independence of the two children. Even if the children are of the same gender, there are still two distinct possibilities. So, let's not use twins as a counterargument.

II. Birthday Paradox

The birthday paradox arises from the question: How many people need to be in a room for there to be at least a 50% chance that two of them share the same birthday?

The answer is 23 people, meaning that if there are 23 people in a room, there's a 50% chance that two of them will have the same birthday. This conclusion seems counterintuitive, hence it is called a paradox. Intuitively, you might think you need at least 183 people to reach a 50% probability, since there are 365 days in a year. However, this isn't the case, and the disbelief stems from two common misconceptions:

The first misconception is misunderstanding the meaning of "exist."

Readers might assume that if there's a 50% chance of a shared birthday among 23 people, it implies:

Suppose there are 22 people in a room, and I join them, there's a 50% chance that one of them shares my birthday. But how can that be possible?

It's not. This thinking is self-centered, whereas the problem's probability describes the group as a whole. "Exist" means any two of the 23 people, involving combinations, largely unrelated to you.

If you want to calculate the probability of someone having the same birthday as you, you can do it like this:

1 - P(22 people have different birthdays from mine) = 1 - (364/365)^22 = 0.06

Doesn't this result seem more reasonable? The birthday paradox doesn't focus on a single individual but rather on the group, including all possible combinations, making the total probability much larger.

The second misconception is thinking that probability changes linearly.

Readers might think that if 23 people give a 50% probability of a shared birthday, then 46 people should give a 100% probability.

This is incorrect. Like a game with a 50% win rate, playing twice doesn't guarantee a 100% win rate. Clearly, playing twice gives a 75% win rate:

P(winning in two tries) = P(winning the first time) + P(not winning the first time but winning the second time) = 1/2 + 1/2*1/2 = 75%

The same logic applies to the birthday paradox. Probability isn't simply additive; it involves a continuous process. Thus, the conclusion isn't unreasonable.

Why is it that with just 23 people, the probability of sharing a birthday exceeds 50%? First, calculate the probability that all 23 have unique (non-repeating) birthdays. With 1 person, the probability is 365/365; with 2 people, it's 365/365 × 364/365, and so on. For 23 people, the probability is:

This calculation yields approximately 0.493, so the probability of at least two people sharing a birthday is 0.507, roughly 50%. In fact, following this method, when the number of people reaches 70, the probability of a shared birthday rises to 99.9%, almost certain. Thus, probabilistically, it's not surprising to find people with the same birthday in a small group of a few dozen people.

3. The Monty Hall Problem

This classic game involves a participant facing three doors. Behind two doors are goats, and behind one door is a car. The participant picks a door, and whatever is behind it becomes theirs (the car is obviously more valuable). The host decides to assist: after the participant chooses a door, the host opens one of the remaining doors to reveal a goat (the host knows what is behind each door). The participant is then given a chance to switch doors. Should they switch or stick with their original choice?

To avoid confusion for those encountering this problem for the first time, let's describe it in more detail:

You are the participant in the game. There are doors 1, 2, and 3. Suppose you randomly choose door 1. The host then opens door 3 and shows you a goat. Should you stick with your initial choice of door 1, or switch to door 2?

The answer is to switch doors. If you switch, the probability of winning the car is 2/3, whereas if you don't switch, it is 1/3. This counterintuitive result might suggest that the probability should be 1/2 since there are two remaining doors, one with a goat and one with a car. However, this is not the case.

Like the boy-girl paradox mentioned earlier, the simplest and safest method is to enumerate all possible outcomes:

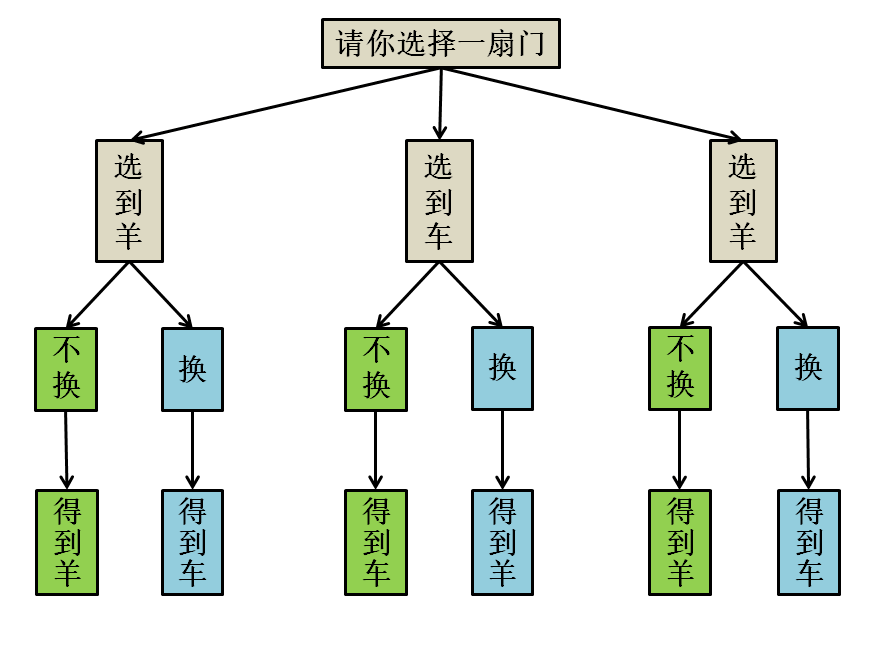
It is clear that the probability of winning by switching doors is 2/3, while not switching gives a probability of 1/3.

There is an even simpler explanation for this problem: the host's action effectively "condenses" the probability. Initially, the chance of choosing the car is 1/3, leaving a probability of 2/3 for the car being behind one of the other two doors. When the host reveals a goat behind one door, the 2/3 probability is transferred to the remaining door. Thus, would you hold onto the 1/3 probability door, or switch to the "condensed" 2/3 probability door?

To make it more intuitive, suppose you have 1 door selected and 2 remaining, and 98 additional doors with goats are added, making 100 doors in total. If asked whether to switch, you would likely refuse, as the probability seems diluted, suggesting the original door is most likely to contain the car. Now, consider starting with 100 doors. You choose one, and the host eliminates 98 goat doors from the remaining 99. Should you switch? Absolutely, because your selected door has a 1% chance, while the other has 99%. Alternatively, not switching is like choosing 1 door, while switching is like choosing 99 doors, making the outcome obvious.

Some readers might have thought about this concept. Consider this: If Xiao Ming, unaware of previous events, barges in to help you decide, knowing only that there are two doors, one with a car and one with a goat, what is his probability of choosing the car?

For Xiao Ming, the probability is 1/2, and this misinterpretation is the root cause of many errors in solving the Monty Hall problem. Similar to the birthday paradox, people often calculate based on their own perspective, which leads to mistakes.

Imagine there are two boxes: Box 1 contains 4 black balls and 2 red balls, while Box 2 contains 2 black balls and 4 red balls. Choosing a box at random, and picking a ball, what is the probability of drawing a red ball?

For Xiao Ming, who is uninformed, he randomly picks a box and a ball, leading to a probability of: 1/2 × 2/6 + 1/2 × 4/6 = 1/2

For you, who is informed and knows the higher probability of drawing from Box 2, the probability is: 0 × 2/6 + 1 × 4/6 = 2/3