How to Efficiently Count Prime Numbers

The definition of a prime number looks very simple: if a number can only be divided by 1 and itself, then this number is a prime.

But even though the definition is simple, not many people can write efficient algorithms related to primes.

For example, LeetCode problem 204 “Count Primes” asks you to write this function:

// return the number of prime numbers in the interval [2, n)
int countPrimes(int n)

// for example, countPrimes(10) returns 4
// because 2, 3, 5, 7 are prime numbers

// return the number of prime numbers in the interval [2, n)
int countPrimes(int n);

// for example, countPrimes(10) returns 4
// because 2, 3, 5, 7 are prime numbers

# Return the number of prime numbers in the interval [2, n)
def countPrimes(n: int) -> int: 

# For example, countPrimes(10) returns 4
# because 2, 3, 5, 7 are prime numbers

// return the number of prime numbers in the interval [2, n)
func countPrimes(n int) int {
}

// for example, countPrimes(10) returns 4
// because 2, 3, 5, 7 are prime numbers

// return the number of prime numbers in the interval [2, n)
var countPrimes = function(n) {
};

// for example, countPrimes(10) returns 4
// because 2,3,5,7 are prime numbers

How would you write this function? Most people will probably write it like this:

int countPrimes(int n) {
    int count = 0;
    for (int i = 2; i < n; i++)
        if (isPrime(i)) count++;
    return count;
}

// determine if the integer n is a prime
boolean isPrime(int n) {
    for (int i = 2; i < n; i++)
        if (n % i == 0)
            // has other divisors
            return false;
    return true;
}

int countPrimes(int n) {
    int count = 0;
    for (int i = 2; i < n; i++)
        if (isPrime(i)) count++;
    return count;
}

// determine if the integer n is a prime number
bool isPrime(int n) {
    for (int i = 2; i < n; i++)
        if (n % i == 0)
            // has other divisors
            return false;
    return true;
}

def countPrimes(n: int) -> int:
    count = 0
    for i in range(2, n):
        if isPrime(i):
            count += 1
    return count

# Determine if the integer n is a prime
def isPrime(n: int) -> bool:
    for i in range(2, n):
        if n % i == 0:
            # There are other divisors
            return False
    return True

func countPrimes(n int) int {
    count := 0
    for i := 2; i < n; i++ {
        if isPrime(i) {
            count++
        }
    }
    return count
}

// determine if the integer n is a prime number
func isPrime(n int) bool {
    for i := 2; i < n; i++ {
        if n % i == 0 {
            // has other divisors
            return false
        }
    }
    return true
}

var countPrimes = function(n) {
    var count = 0;
    for (var i = 2; i < n; i++) {
        if (isPrime(i)) count++;
    }
    return count;
};

// determine if the integer n is a prime number
var isPrime = function(n) {
    for (var i = 2; i < n; i++) {
        if (n % i === 0) {
            // has other divisors
            return false;
        }
    }
    return true;
}

With this code, the time complexity is O(n^2), which is too slow. The main issues are: using the isPrime helper function is not efficient enough, and even if you use it, this version still has a lot of repeated computation.

First, let’s see how to correctly check if a number is prime. You only need to change the for-loop condition in the isPrime code:

boolean isPrime(int n) {
    for (int i = 2; i * i <= n; i++)
        ...
}

In other words, i does not need to go up to n. It only needs to go up to sqrt(n).

This is a basic fact in number theory: if a number $n$ is not prime, then it must have a factor less than or equal to $\sqrt{n}$.

Take n = 12 as an example:

12 = 2 × 6
12 = 3 × 4
12 = sqrt(12) × sqrt(12)
12 = 4 × 3
12 = 6 × 2

You can see that the last two products are just the first two reversed, and the turning point is at sqrt(n).

So, if you do not find any factor in the range [2, sqrt(n)], you can say n is a prime. That also means there will be no factor in the range [sqrt(n), n].

Now the time complexity of the isPrime function is $O(\sqrt{N}). **But actually, we do not need this function to implement countPrimes**. I only want you to understand the idea of sqrt(n)` here, because we will use it again later.

Efficiently Implement countPrimes

The next method is called the "Sieve of Eratosthenes". It was invented by an ancient Greek scholar named Eratosthenes. We saw his name in middle school textbooks, because he was the first person to correctly compute the Earth's circumference using shadows. He is known as the "father of geography".

Back to the topic, the key idea of the sieve is the opposite of the normal method above:

Start from 2. We know 2 is a prime number. Then 2 × 2 = 4, 3 × 2 = 6, 4 × 2 = 8... all cannot be prime.

Next we see that 3 is also prime. Then 3 × 2 = 6, 3 × 3 = 9, 3 × 4 = 12... also cannot be prime.

This GIF from Wikipedia shows the process clearly:

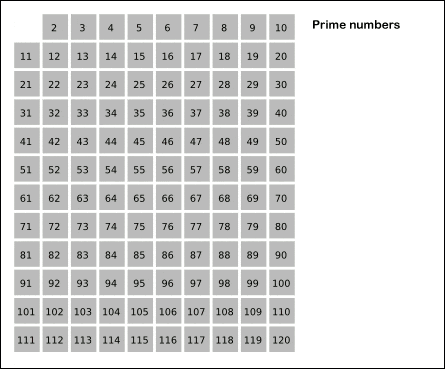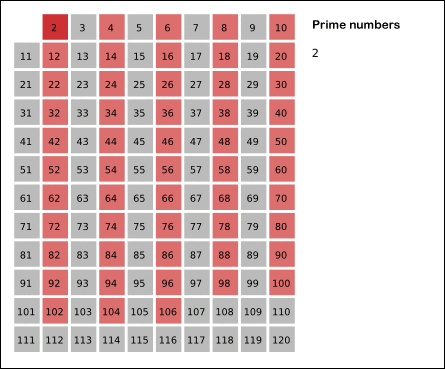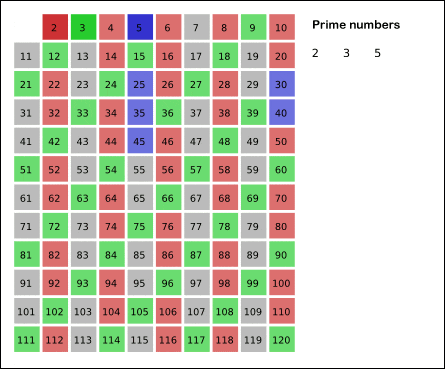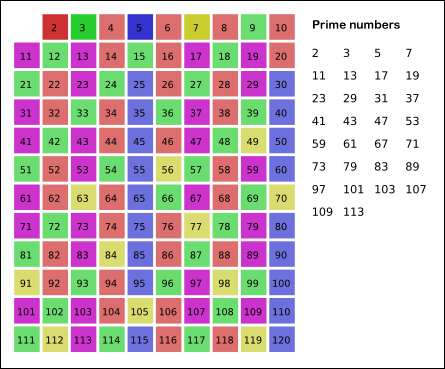
By now, you may already understand the logic of this elimination method. Here is our first version of the code:

class Solution {
    public int countPrimes(int n) {
        boolean[] isPrime = new boolean[n];
        // initialize the array to true
        Arrays.fill(isPrime, true);

        for (int i = 2; i < n; i++) {
            if (isPrime[i]) {
                // multiples of i cannot be prime
                for (int j = 2 * i; j < n; j += i) {
                    isPrime[j] = false;
                }
            }
        }
        
        int count = 0;
        for (int i = 2; i < n; i++) {
            if (isPrime[i]) count++;
        }
        
        return count;
    }
}

class Solution {
public:
    int countPrimes(int n) {
        // initialize the array to true
        vector<bool> isPrime(n, true);
        for (int i = 2; i < n; i++) {
            if (isPrime[i]) {
                // multiples of i cannot be prime
                for (int j = 2 * i; j < n; j += i) {
                    isPrime[j] = false;
                }
            }
        }
        
        int count = 0;
        for (int i = 2; i < n; i++) {
            if (isPrime[i]) {
                count++;
            }
        }
        
        return count;
    }
};

class Solution:
    def countPrimes(self, n: int) -> int:
        # initialize the array to true
        isPrime = [True] * n
        for i in range(2, n):
            if isPrime[i]:
                # multiples of i cannot be prime
                for j in range(2 * i, n, i):
                    isPrime[j] = False

        count = 0
        for i in range(2, n):
            if isPrime[i]: 
                count += 1

        return count

func countPrimes(n int) int {
    isPrime := make([]bool, n)
    // initialize the array to true
    for i := 0; i < n; i++ {
        isPrime[i] = true
    }

    for i := 2; i < n; i++ {
        if isPrime[i] {
            // multiples of i cannot be prime
            for j := 2 * i; j < n; j += i {
                isPrime[j] = false
            }
        }
    }
    count := 0
    for i := 2; i < n; i++ {
        if isPrime[i] {
            count++
        }
    }
    return count
}

var countPrimes = function(n) {
    // initialize the array to true
    let isPrime = new Array(n).fill(true);
    for (let i = 2; i < n; i++) {
        if (isPrime[i]) {
            // multiples of i cannot be prime
            for (let j = 2 * i; j < n; j += i) {
                isPrime[j] = false;
            }
        }
    }
    
    let count = 0;
    for (let i = 2; i < n; i++) {
        if (isPrime[i]) count++;
    }
    
    return count;
};

If you understand the code above, you already know the main idea. But there are still two small optimizations.

First, think about the isPrime function at the beginning of this article. Because of factor symmetry, the for loop only needs to check [2, sqrt(n)]. Here it is similar: the outer for loop only needs to go up to sqrt(n):

for (int i = 2; i * i < n; i++) 
    if (isPrime[i]) 
        ...

Besides that, it is easy to miss that the inner for loop can also be optimized. Before, we wrote:

for (int j = 2 * i; j < n; j += i) 
    isPrime[j] = false;

This marks all multiples of i as false, but there is still extra work.

For example, when n = 25 and i = 5, the algorithm will mark 5 × 2 = 10, 5 × 3 = 15, and so on. But these numbers were already marked by i = 2 and i = 3 as 2 × 5 and 3 × 5.

We can improve it a bit and let j start from i * i instead of 2 * i:

for (int j = i * i; j < n; j += i) 
    isPrime[j] = false;

Now the prime counting algorithm is efficient. Here is the final complete code:

class Solution {
    public int countPrimes(int n) {
        boolean[] isPrime = new boolean[n];
        Arrays.fill(isPrime, true);
        for (int i = 2; i * i < n; i++)
            if (isPrime[i])
                for (int j = i * i; j < n; j += i)
                    isPrime[j] = false;

        int count = 0;
        for (int i = 2; i < n; i++)
            if (isPrime[i]) count++;

        return count;
    }
}

class Solution {
public:
    int countPrimes(int n) {
        vector<bool> isPrime(n, true);
        for (int i = 2; i * i < n; i++) {
            if (isPrime[i]) {
                for (int j = i * i; j < n; j += i) {
                    isPrime[j] = false;
                }
            }
        }
        
        int count = 0;
        for (int i = 2; i < n; i++) {
            if (isPrime[i]) {
                count++;
            }
        }
        
        return count;
    }
};

class Solution:
    def countPrimes(self, n: int) -> int:
        isPrime = [True] * n
        for i in range(2, int(n ** 0.5) + 1):
            if isPrime[i]:
                for j in range(i * i, n, i):
                    isPrime[j] = False

        count = 0
        for i in range(2, n):
            if isPrime[i]: 
                count += 1

        return count

func countPrimes(n int) int {
    isPrime := make([]bool, n)
    for i := 0; i < n; i++ {
        isPrime[i] = true
    }

    for i := 2; i * i < n; i++ {
        if isPrime[i] {
            for j := i * i; j < n; j += i {
                isPrime[j] = false
            }
        }
    }
    count := 0
    for i := 2; i < n; i++ {
        if isPrime[i] {
            count++
        }
    }
    return count
}

var countPrimes = function(n) {
    let isPrime = new Array(n).fill(true);
    for (let i = 2; i * i < n; i++) {
        if (isPrime[i]) {
            for (let j = i * i; j < n; j += i) {
                isPrime[j] = false;
            }
        }
    }
    
    let count = 0;
    for (let i = 2; i < n; i++) {
        if (isPrime[i]) count++;
    }
    
    return count;
};

The time complexity of this algorithm is not easy to compute. Clearly, the time depends on the two nested for loops. The number of operations is about:

  n/2 + n/3 + n/5 + n/7 + ...
= n × (1/2 + 1/3 + 1/5 + 1/7...)

The part in brackets is the sum of the reciprocals of primes. The final result is $O(N * \log\log N)$. If you are interested, you can look up the proof of this time complexity.

This is all for the prime counting algorithm. As you can see, even a simple problem can have many details to polish.