How to Determine if a Rectangle is Perfect

Today we will look at a very interesting and challenging problem.

We know that a rectangle has four corners, but you only need the coordinates of two corners to define a rectangle (for example, the bottom-left and top-right corners).

Let's look at LeetCode problem 391: Perfect Rectangle. The problem gives you an array rectangles, where each element is a tuple (x1, y1, x2, y2). This tuple records the bottom-left and top-right coordinates of a small rectangle.

391. Perfect Rectangle | LeetCode |  🔴

Given an array rectangles where rectangles[i] = [xi, yi, ai, bi] represents an axis-aligned rectangle. The bottom-left point of the rectangle is (xi, yi) and the top-right point of it is (ai, bi).

Return true if all the rectangles together form an exact cover of a rectangular region.

Example 1:

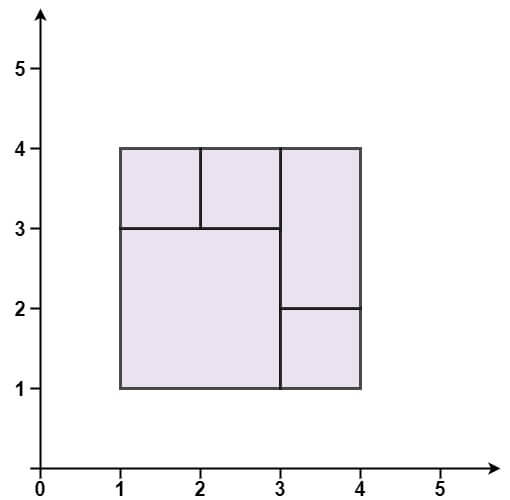
Input: rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]
Output: true
Explanation: All 5 rectangles together form an exact cover of a rectangular region.

Example 2:

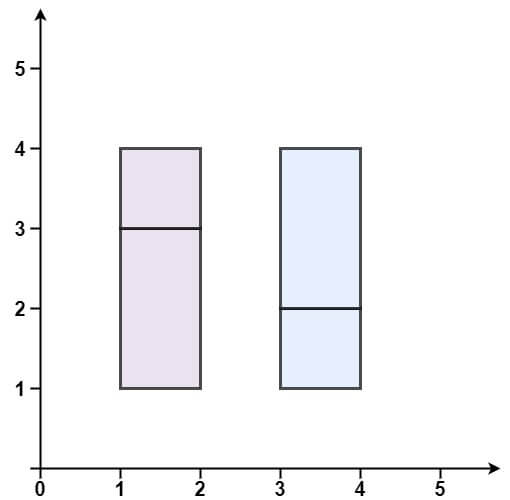
Input: rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]
Output: false
Explanation: Because there is a gap between the two rectangular regions.

Example 3:

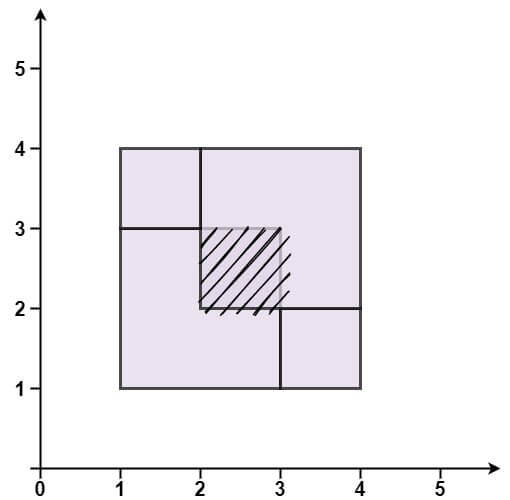
Input: rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]]
Output: false
Explanation: Because two of the rectangles overlap with each other.

Constraints:

• 1 <= rectangles.length <= 2 * 104
• rectangles[i].length == 4
• -105 <= xi, yi, ai, bi <= 105

The problem is from LeetCode 391. Perfect Rectangle.

In other words, the rectangles array contains many small rectangles. The problem asks us to return a boolean value to check if these small rectangles can form a "perfect rectangle." The function signature is as follows:

boolean isRectangleCover(int[][] rectangles)

bool isRectangleCover(vector<vector<int>>& rectangles)

def isRectangleCover(rectangles: List[List[int]]) -> bool

func isRectangleCover(rectangles [][]int) bool {}

function isRectangleCover(rectangles) {}

A "perfect rectangle" means that all the small rectangles together form one big rectangle, with no overlaps and no gaps.

This problem is rated Hard on LeetCode. If you have not seen similar problems before, it can be tricky.

The usual way is to try to represent the final shape, and then check if any two rectangles overlap or if there are gaps. This is possible, but the logic can get very complicated.

Actually, to check if the final shape is a perfect rectangle, we need to look at two things: "area" and "corners."

Let's talk about the "area" first.

Each element in the rectangles array is a tuple (x1, y1, x2, y2), which gives the bottom-left and top-right coordinates of a small rectangle.

If these small rectangles form a "perfect rectangle," can you find the bottom-left corner (X1, Y1) and the top-right corner (X2, Y2) of the big rectangle?

This is simple. The bottom-left corner (X1, Y1) is the minimum of all small rectangles' bottom-left corners. The top-right corner (X2, Y2) is the maximum of all small rectangles' top-right corners.

Here, we use lowercase letters for the small rectangles' coordinates, and uppercase for the perfect rectangle's coordinates. You can write code like this:

// The bottom-left vertex, initialized to positive infinity to record the minimum value
double X1 = Double.POSITIVE_INFINITY, Y1 = Double.POSITIVE_INFINITY;

// The top-right vertex, initialized to negative infinity to record the maximum value
double X2 = Double.NEGATIVE_INFINITY, Y2 = Double.NEGATIVE_INFINITY;

for(int[] rectangle : rectangles){
    int x1 = rectangle[0], y1 = rectangle[1], x2 = rectangle[2], y2 = rectangle[3];

    // Take the minimum value of the bottom-left vertex of the small rectangle
    X1 = Math.min(X1, x1);
    Y1 = Math.min(Y1, y1);

    // Take the maximum value of the top-right vertex of the small rectangle
    X2 = Math.max(X2, x2);
    Y2 = Math.max(Y2, y2);
}

// The bottom-left vertex, initialized to positive infinity to record the minimum value
int X1 = INT_MAX, Y1 = INT_MAX;
// The top-right vertex, initialized to negative infinity to record the maximum value
int X2 = INT_MIN, Y2 = INT_MIN;

for(auto &rectangle : rectangles) {
    int x1 = rectangle[0], y1 = rectangle[1], x2 = rectangle[2], y2 = rectangle[3];
    // Take the minimum value of the bottom-left vertex of the small rectangle
    X1 = min(X1, x1); Y1 = min(Y1, y1);
    // Take the maximum value of the top-right vertex of the small rectangle
    X2 = max(X2, x2); Y2 = max(Y2, y2);
}

# The bottom-left vertex, initialized to positive infinity to record the minimum value
X1, Y1 = inf, inf
# The top-right vertex, initialized to negative infinity to record the maximum value
X2, Y2 = -inf, -inf

for x1, y1, x2, y2 in rectangles:
    # Take the minimum value of the bottom-left vertex of the small rectangle
    X1, Y1 = min(X1, x1), min(Y1, y1)
    # Take the maximum value of the top-right vertex of the small rectangle
    X2, Y2 = max(X2, x2), max(Y2, y2)

// The bottom-left vertex, initialized to positive infinity to record the minimum value
var X1, Y1 float64 = math.MaxFloat64, math.MaxFloat64

// The top-right vertex, initialized to negative infinity to record the maximum value
var X2, Y2 float64 = math.SmallestNonzeroFloat64, math.SmallestNonzeroFloat64

for _, rectangle := range rectangles {
    x1, y1, x2, y2 := rectangle[0], rectangle[1], rectangle[2], rectangle[3]
    // Take the minimum value of the bottom-left vertex of the small rectangle
    X1, Y1 = math.Min(X1, x1), math.Min(Y1, y1)
    // Take the maximum value of the top-right vertex of the small rectangle
    X2, Y2 = math.Max(X2, x2), math.Max(Y2, y2)
}

// The bottom-left vertex, initialized to positive infinity to record the minimum value
var X1 = Number.POSITIVE_INFINITY, Y1 = Number.POSITIVE_INFINITY;
// The top-right vertex, initialized to negative infinity to record the maximum value
var X2 = Number.NEGATIVE_INFINITY, Y2 = Number.NEGATIVE_INFINITY;

for (let i = 0; i < rectangles.length; i++) {
    let rectangle = rectangles[i];
    // Take the minimum value of the bottom-left vertex of the small rectangle
    X1 = Math.min(X1, rectangle[0]);
    Y1 = Math.min(Y1, rectangle[1]);
    // Take the maximum value of the top-right vertex of the small rectangle
    X2 = Math.max(X2, rectangle[2]);
    Y2 = Math.max(Y2, rectangle[3]);
}

Now you have the bottom-left corner (X1, Y1) and the top-right corner (X2, Y2) of the perfect rectangle.

The calculated X1, Y1, X2, Y2 are the "theoretical coordinates" of the perfect rectangle. If the sum of the areas of all small rectangles is not equal to the area of this perfect rectangle, there must be overlaps or gaps. Then it is not a perfect rectangle.

Here is the next step in code:

boolean isRectangleCover(int[][] rectangles) {
    int X1 = Integer.MAX_VALUE, Y1 = Integer.MAX_VALUE;
    int X2 = Integer.MIN_VALUE, Y2 = Integer.MIN_VALUE;
    // record the sum of the areas of all small rectangles
    int actualArea = 0;
    for (int[] rect : rectangles) {
        int x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
        // calculate the theoretical coordinates of the perfect rectangle
        X1 = Math.min(X1, x1);
        Y1 = Math.min(Y1, y1);
        X2 = Math.max(X2, x2);
        Y2 = Math.max(Y2, y2);
        // accumulate the area of all small rectangles
        actualArea += (x2 - x1) * (y2 - y1);
    }

    // calculate the theoretical area of the perfect rectangle
    int expectedArea = (X2 - X1) * (Y2 - Y1);
    // the areas should be the same
    if (actualArea != expectedArea) {
        return false;
    }

    return true;
}

bool isRectangleCover(vector<vector<int>>& rectangles) {
    int X1 = numeric_limits<int>::max(), Y1 = numeric_limits<int>::max();
    int X2 = numeric_limits<int>::min(), Y2 = numeric_limits<int>::min();
    // record the sum of the areas of all small rectangles
    int actualArea = 0;
    for (vector<int>& rect : rectangles) {
        int x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
        // calculate the theoretical coordinates of the perfect rectangle
        X1 = min(X1, x1);
        Y1 = min(Y1, y1);
        X2 = max(X2, x2);
        Y2 = max(Y2, y2);
        // accumulate the area of all small rectangles
        actualArea += (x2 - x1) * (y2 - y1);
    }

    // calculate the theoretical area of the perfect rectangle
    int expectedArea = (X2 - X1) * (Y2 - Y1);
    // the areas should be the same
    if (actualArea != expectedArea) {
        return false;
    }

    return true;
}

def isRectangleCover(rectangles):
    X1, Y1 = float('inf'), float('inf')
    X2, Y2 = float('-inf'), float('-inf')
    # record the sum of the areas of all small rectangles
    actualArea = 0
    for rect in rectangles:
        x1, y1, x2, y2 = rect
        # calculate the theoretical coordinates of the perfect rectangle
        X1 = min(X1, x1)
        Y1 = min(Y1, y1)
        X2 = max(X2, x2)
        Y2 = max(Y2, y2)
        # accumulate the area of all small rectangles
        actualArea += (x2 - x1) * (y2 - y1)

    # calculate the theoretical area of the perfect rectangle
    expectedArea = (X2 - X1) * (Y2 - Y1)
    # the areas should be the same
    if actualArea != expectedArea:
        return False

    return True

func isRectangleCover(rectangles [][]int) bool {
    X1, Y1, X2, Y2 := math.MaxInt64, math.MaxInt64, math.MinInt64, math.MinInt64
    // record the sum of the areas of all small rectangles
    actualArea := 0
    for _, rect := range rectangles {
        x1, y1, x2, y2 := rect[0], rect[1], rect[2], rect[3]
        // calculate the theoretical coordinates of the perfect rectangle
        X1 = min(X1, x1)
        Y1 = min(Y1, y1)
        X2 = max(X2, x2)
        Y2 = max(Y2, y2)
        // accumulate the area of all small rectangles
        actualArea += (x2 - x1) * (y2 - y1)
    }

    // calculate the theoretical area of the perfect rectangle
    expectedArea := (X2 - X1) * (Y2 - Y1)
    // the areas should be the same
    if actualArea != expectedArea {
        return false
    }

    return true
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

func min(a, b int) int {
    if a < b {
        return a
    }
    return b
}

var isRectangleCover = function(rectangles) {
    var X1 = Number.MAX_VALUE, Y1 = Number.MAX_VALUE;
    var X2 = Number.MIN_VALUE, Y2 = Number.MIN_VALUE;
    // record the sum of the areas of all small rectangles
    var actualArea = 0;
    for (var rect of rectangles) {
        var x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
        // calculate the theoretical coordinates of the perfect rectangle
        X1 = Math.min(X1, x1);
        Y1 = Math.min(Y1, y1);
        X2 = Math.max(X2, x2);
        Y2 = Math.max(Y2, y2);
        // accumulate the area of all small rectangles
        actualArea += (x2 - x1) * (y2 - y1);
    }

    // calculate the theoretical area of the perfect rectangle
    var expectedArea = (X2 - X1) * (Y2 - Y1);
    // the areas should be the same
    if (actualArea !== expectedArea) {
        return false;
    }

    return true;
}

This covers the "area" part. The idea is simple: if the sum of the small rectangles' areas is not equal to the area of the perfect rectangle, then there must be overlaps or gaps, so it is not a perfect rectangle.

But what if the two areas are equal? Can we be sure the shape is a perfect rectangle, with no gaps or overlaps?

No, we cannot. Here is a simple example: Imagine a perfect rectangle. Now, cut out a small rectangle from the middle, and move it down by one unit. The total area stays the same, but now there is a gap and an overlap. It is no longer a perfect rectangle.

In summary, even if the areas are equal, we cannot be sure there are no gaps or overlaps. So, we also need to check the "corners".

Do you remember a logic puzzle from elementary school? If you cut a rectangle along its diagonal, how many corners are left? The answer: if you cut along the diagonal, there are 3 corners left; if you cut horizontally or vertically, there are 4; if you cut off a small corner, there are 5 corners.

Let’s return to this problem. Our next steps will use a little bit of this kind of logical thinking.

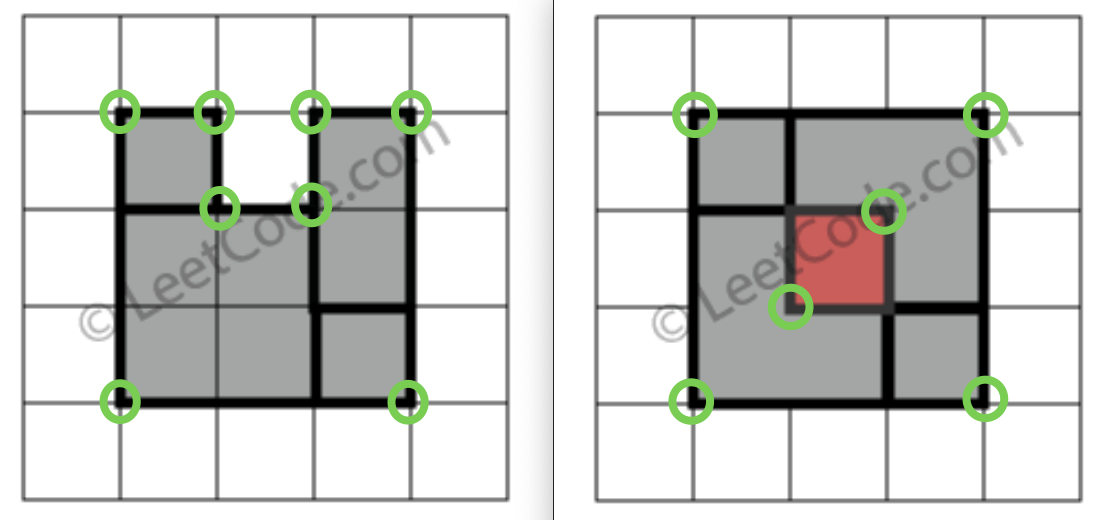
Clearly, a perfect rectangle must have exactly four corners. By definition, a rectangle should have four corners. If there are missing corners or overlaps, there will be more than four corners. For example, in the two sample cases below, there are more than four corners:

If we can find out how many vertices the final shape made from all the small rectangles in rectangles has, we can check if the shape is a perfect rectangle.

But how are these vertices formed? We can see them easily, but how can we make the computer, or an algorithm, know if a point is a vertex? This is the main challenge of this problem.

Look at the four cases below:

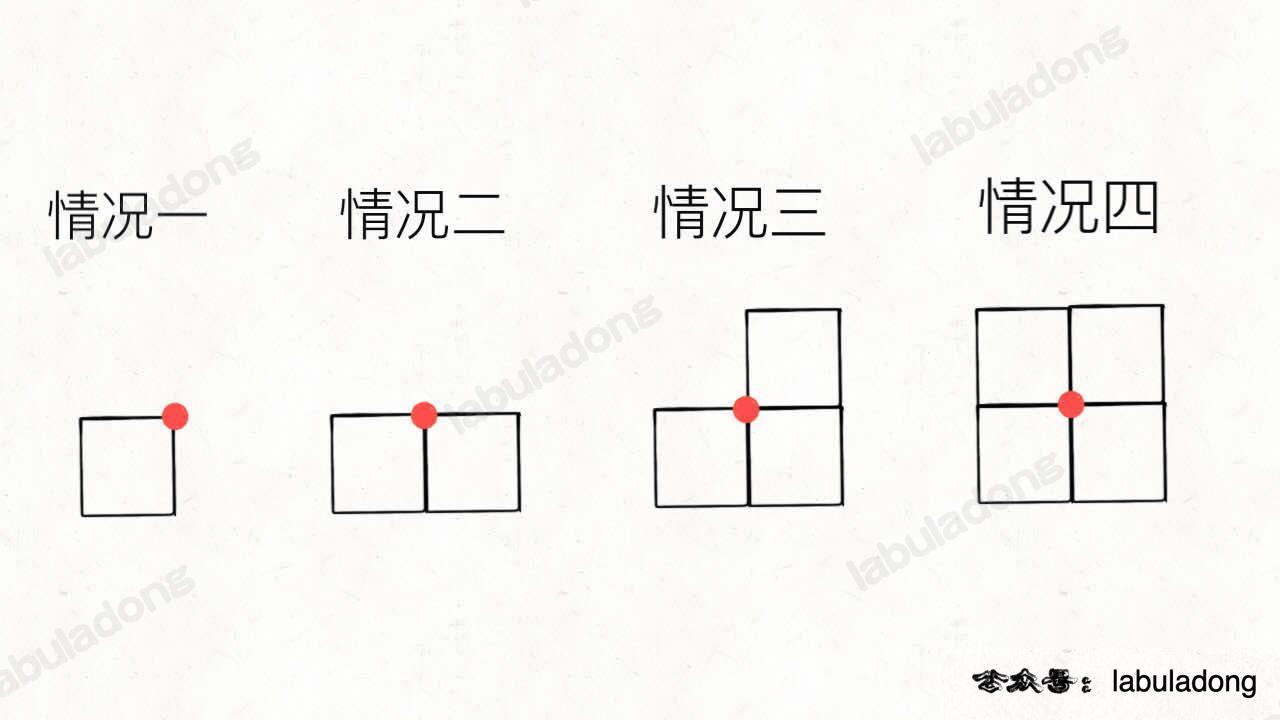
In the picture, when is the red dot a vertex, and when is it not? Clearly, in case one and case three, the red dot is a vertex. In case two and case four, it is not a vertex.

In other words, if a point is a vertex of 2 or 4 small rectangles, it is not a vertex in the final shape; if a point is a vertex of 1 or 3 small rectangles, it is a vertex in the final shape.

Notice that 2 and 4 are even numbers, while 1 and 3 are odd numbers. We want to count how many vertices appear an odd number of times in the final shape. We can write code like this:

boolean isRectangleCover(int[][] rectangles) {
    int X1 = Integer.MAX_VALUE, Y1 = Integer.MAX_VALUE;
    int X2 = Integer.MIN_VALUE, Y2 = Integer.MIN_VALUE;

    int actualArea = 0;
    // Hash set to record the vertices of the final figure
    Set<String> points = new HashSet<>();
    for (int[] rect : rectangles) {
        int x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
        X1 = Math.min(X1, x1);
        Y1 = Math.min(Y1, y1);
        X2 = Math.max(X2, x2);
        Y2 = Math.max(Y2, y2);

        actualArea += (x2 - x1) * (y2 - y1);
        // First calculate the coordinates of each point of the small
        // rectangle, represented by a string, for easy storage in the hash set
        String p1 = x1 + "," + y1;
        String p2 = x1 + "," + y2;
        String p3 = x2 + "," + y1;
        String p4 = x2 + "," + y2;
        // For each point, if it exists in the set, remove it;
        // if it does not exist in the set, add it;
        // The remaining points in the set are those that appear an odd number of times
        for (String p : new String[]{p1, p2, p3, p4}) {
            if (points.contains(p)) {
                points.remove(p);
            } else {
                points.add(p);
            }
        }
    }

    int expectedArea = (X2 - X1) * (Y2 - Y1);
    if (actualArea != expectedArea) {
        return false;
    }

    // Check the number of vertices
    if (points.size() != 4 || 
        !points.contains(X1 + "," + Y1) || 
        !points.contains(X1 + "," + Y2) || 
        !points.contains(X2 + "," + Y1) || 
        !points.contains(X2 + "," + Y2)) {
        return false;
    }

    return true;
}

bool isRectangleCover(vector<vector<int>>& rectangles) {
    int X1 = INT_MAX, Y1 = INT_MAX;
    int X2 = INT_MIN, Y2 = INT_MIN;

    int actualArea = 0;
    // Hash set to record the vertices of the final shape
    unordered_set<string> points;

    for (auto &rect : rectangles) {
        int x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
        X1 = min(X1, x1);
        Y1 = min(Y1, y1);
        X2 = max(X2, x2);
        Y2 = max(Y2, y2);

        actualArea += (x2 - x1) * (y2 - y1);
        // First calculate the coordinates of each point of the small
        // rectangle, represented by a string, for easy storage in the hash set
        string p1 = to_string(x1) + "," + to_string(y1);
        string p2 = to_string(x1) + "," + to_string(y2);
        string p3 = to_string(x2) + "," + to_string(y1);
        string p4 = to_string(x2) + "," + to_string(y2);

        vector<string> pointArr = {p1, p2, p3, p4};
        // For each point, if it exists in the set, remove it;
        // if it does not exist in the set, add it;
        // The remaining points in the set are those that appear an odd number of times
        for (auto &p : pointArr) {
            if (points.count(p)) {
                points.erase(p);
            } else {
                points.insert(p);
            }
        }
    }

    int expectedArea = (X2 - X1) * (Y2 - Y1);
    if (actualArea != expectedArea) {
        return false;
    }

    // Check the number of vertices
    if (points.size() != 4 || 
        !points.count(to_string(X1) + "," + to_string(Y1)) || 
        !points.count(to_string(X1) + "," + to_string(Y2)) || 
        !points.count(to_string(X2) + "," + to_string(Y1)) || 
        !points.count(to_string(X2) + "," + to_string(Y2))) {
        return false;
    }

    return true;
}

def isRectangleCover(rectangles):
    X1, Y1, X2, Y2 = float('inf'), float('inf'), float('-inf'), float('-inf')

    actualArea = 0
    # Hash set to record the vertices of the final shape
    points = set()
    for rect in rectangles:
        x1, y1, x2, y2 = rect
        X1 = min(X1, x1)
        Y1 = min(Y1, y1)
        X2 = max(X2, x2)
        Y2 = max(Y2, y2)

        actualArea += (x2 - x1) * (y2 - y1)
        # First calculate the coordinates of each point of the small
        # rectangle, represented by a string for easy storage in the hash set
        p1 = str(x1) + "," + str(y1)
        p2 = str(x1) + "," + str(y2)
        p3 = str(x2) + "," + str(y1)
        p4 = str(x2) + "," + str(y2)

        pointArr = [p1, p2, p3, p4]
        # For each point, if it exists in the set, remove it;
        for p in pointArr:
            if p in points:
                points.remove(p)
            else:
                points.add(p)
        # If it does not exist in the set, add it;
        # The remaining points in the set are those that appear an odd number of times
        
    expectedArea = (X2 - X1) * (Y2 - Y1)
    if actualArea != expectedArea:
        return False

    # Check the number of vertices
    if len(points) != 4 or \
        str(X1) + "," + str(Y1) not in points or \
        str(X1) + "," + str(Y2) not in points or \
        str(X2) + "," + str(Y1) not in points or \
        str(X2) + "," + str(Y2) not in points:
        return False

    return True

func isRectangleCover(rectangles [][]int) bool {
    X1, Y1 := math.MaxInt32, math.MaxInt32
    X2, Y2 := math.MinInt32, math.MinInt32
  
    var actualArea int
    // hash set to record the vertices of the final shape
    points := map[string]bool{}

    for _, rect := range rectangles{
        x1 := rect[0]
        y1 := rect[1]
        x2 := rect[2]
        y2 := rect[3]

        X1 = int(math.Min(float64(X1), float64(x1)))
        Y1 = int(math.Min(float64(Y1), float64(y1)))
        X2 = int(math.Max(float64(X2), float64(x2)))
        Y2 = int(math.Max(float64(Y2), float64(y2)))

        // calculate the area of the small rectangle
        actualArea += (x2 - x1) * (y2 - y1)

        // first calculate the coordinates of each point of the small rectangle,
        // represent them as strings for easy storage in the hash set
        p1 := fmt.Sprintf("%d,%d", x1, y1)
        p2 := fmt.Sprintf("%d,%d", x1, y2)
        p3 := fmt.Sprintf("%d,%d", x2, y1)
        p4 := fmt.Sprintf("%d,%d", x2, y2)

        pointArr := []string{p1, p2, p3, p4}
        // for each point, if it exists in the set, remove it;
        // if it does not exist in the set, add it;
        // the remaining points in the set are those that appear an odd number of times
        for _, p := range pointArr{
            if _, exists := points[p]; exists{
                delete(points, p)
            } else {
                points[p] = true
            }
        }
    }

    expectedArea := (X2 - X1) * (Y2 - Y1)
    if actualArea != expectedArea {
        return false
    }

    // check the number of vertices
    if len(points) != 4 {
        return false
    }

    if _, ex := points[fmt.Sprintf("%d,%d", X1, Y1)];!ex{
        return false
    }

    if _, ex := points[fmt.Sprintf("%d,%d", X1, Y2)];!ex{
        return false
    }

    if _, ex := points[fmt.Sprintf("%d,%d", X2, Y1)];!ex{
        return false
    }

    if _, ex := points[fmt.Sprintf("%d,%d", X2, Y2)];!ex{
        return false
    }

    return true
}

var isRectangleCover = function(rectangles) {
    var X1 = Number.MAX_VALUE, Y1 = Number.MAX_VALUE;
    var X2 = Number.MIN_VALUE, Y2 = Number.MIN_VALUE;

    var actualArea = 0;
    // Hash set to record the vertices of the final shape
    var points = new Set();
    for (var rect of rectangles) {
        var x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
        X1 = Math.min(X1, x1);
        Y1 = Math.min(Y1, y1);
        X2 = Math.max(X2, x2);
        Y2 = Math.max(Y2, y2);

        actualArea += (x2 - x1) * (y2 - y1);

        // First calculate the coordinates of each point of the small
        // rectangle, represented as a string for easy storage in the hash set
        var p1 = x1 + "," + y1;
        var p2 = x1 + "," + y2;
        var p3 = x2 + "," + y1;
        var p4 = x2 + "," + y2;

        // For each point, if it exists in the set, delete it;
        // If it does not exist in the set, add it;
        // The remaining points in the set are those that appear an odd number of times
        for (var p of [p1, p2, p3, p4]) {
            if (points.has(p)) {
                points.delete(p);
            } else {
                points.add(p);
            }
        }
    }

    var expectedArea = (X2 - X1) * (Y2 - Y1);
    if (actualArea !== expectedArea) {
        return false;
    }

    // Check the number of vertices
    if (points.size != 4 || 
        !points.has(X1 + "," + Y1) || 
        !points.has(X1 + "," + Y2) || 
        !points.has(X2 + "," + Y1) || 
        !points.has(X2 + "," + Y2)) {
        return false;
    }

    return true;
};

In this code, we use a points set to record the coordinates of all the vertices of the final shape made by the small rectangles in rectangles. The key logic is how we add coordinates to the points set:

If a vertex p is already in the points set, remove it; if it is not in the set, add it.

This simple logic makes sure that, at the end, only vertices that appear 1 or 3 times remain in the points set. Vertices that appear 2 or 4 times are removed.

So, we might think, in the end, the points set should have exactly 4 vertices. If len(points) != 4, the final shape is definitely not a perfect rectangle.

But is it enough to say that if len(points) == 4, the shape is a perfect rectangle? Not really, because the problem does not say the small rectangles in rectangles cannot overlap. Look at this case:

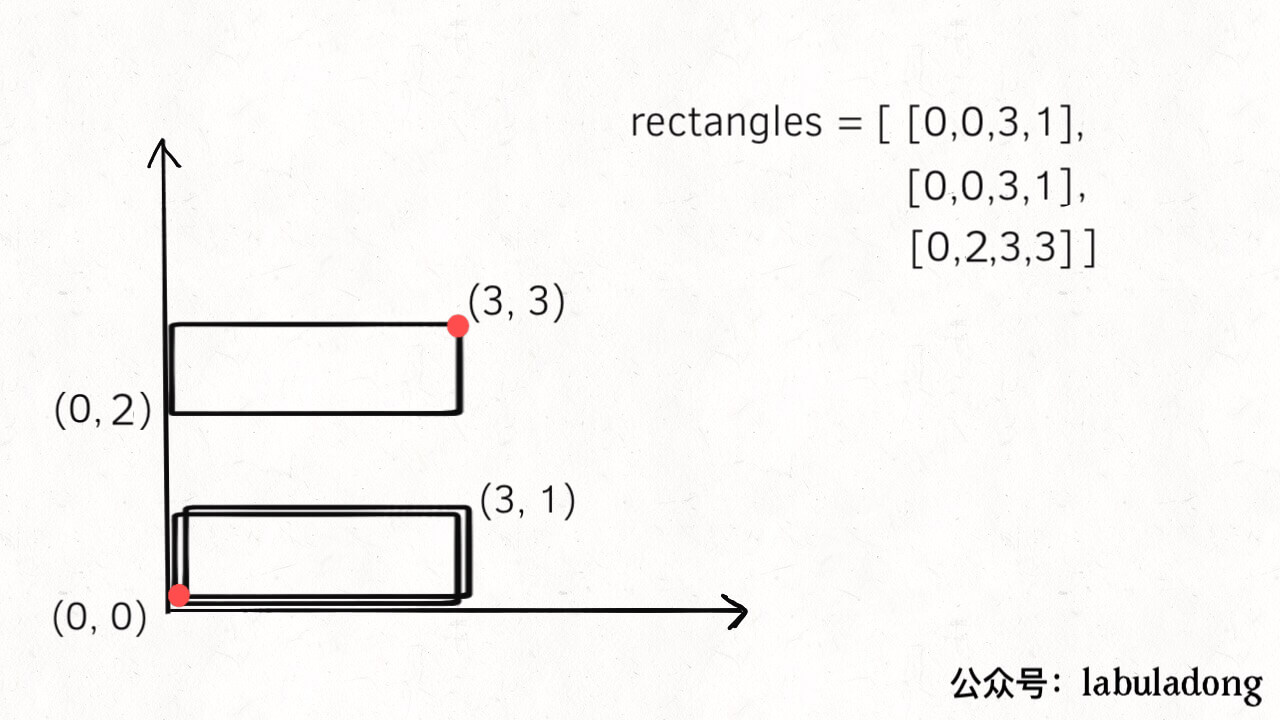
Here, two rectangles overlap. According to our logic, their vertices are removed, and only four vertices are left. If you check the area, the calculated area and the theoretical area (based on the red points) are the same. But clearly, this is not what the problem wants as a perfect rectangle.

So, not only do we need to check len(points) == 4, but we also need to make sure that the coordinates of the remaining points in points match the four theoretical vertices of a perfect rectangle. Here is the code:

class Solution {
    public boolean isRectangleCover(int[][] rectangles) {
        int X1 = Integer.MAX_VALUE, Y1 = Integer.MAX_VALUE;
        int X2 = Integer.MIN_VALUE, Y2 = Integer.MIN_VALUE;
        
        Set<String> points = new HashSet<>();
        int actualArea = 0;
        for (int[] rect : rectangles) {
            int x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
            // calculate the theoretical vertex coordinates of the perfect rectangle
            X1 = Math.min(X1, x1);
            Y1 = Math.min(Y1, y1);
            X2 = Math.max(X2, x2);
            Y2 = Math.max(Y2, y2);
            // accumulate the area of the small rectangle
            actualArea += (x2 - x1) * (y2 - y1);
            // the final vertices of the formed shape
            String p1 = x1 + "," + y1;
            String p2 = x1 + "," + y2;
            String p3 = x2 + "," + y1;
            String p4 = x2 + "," + y2;
            for (String p : new String[]{p1, p2, p3, p4}) {
                if (points.contains(p)) points.remove(p);
                else                    points.add(p);
            }
        }
        // check if the area is the same
        int expectedArea = (X2 - X1) * (Y2 - Y1);
        if (actualArea != expectedArea) {
            return false;
        }
        // check if the number of vertices is 4
        if (points.size() != 4) {
            return false;
        }
        // check if the 4 vertices left belong to the perfect rectangle
        if (!points.contains(X1 + "," + Y1)) return false;
        if (!points.contains(X1 + "," + Y2)) return false;
        if (!points.contains(X2 + "," + Y1)) return false;
        if (!points.contains(X2 + "," + Y2)) return false;
        // if the area and vertices match, the rectangle meets the requirements
        return true;
    }
}

#include <vector>
#include <set>
#include <climits>
#include <string>
#include <algorithm>

using namespace std;

class Solution {
public:
    bool isRectangleCover(vector<vector<int>>& rectangles) {
        int X1 = INT_MAX, Y1 = INT_MAX;
        int X2 = INT_MIN, Y2 = INT_MIN;
        
        set<string> points;
        long long actualArea = 0; // Change type to long long to avoid overflow
        for (const auto& rect : rectangles) {
            int x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
            // calculate the theoretical vertex coordinates of the perfect rectangle
            X1 = min(X1, x1);
            Y1 = min(Y1, y1);
            X2 = max(X2, x2);
            Y2 = max(Y2, y2);
            // accumulate the area of the small rectangle
            actualArea += static_cast<long long>(x2 - x1) * (y2 - y1); // Cast to long long before multiplication
            // the final vertices of the formed shape
            string p1 = to_string(x1) + "," + to_string(y1);
            string p2 = to_string(x1) + "," + to_string(y2);
            string p3 = to_string(x2) + "," + to_string(y1);
            string p4 = to_string(x2) + "," + to_string(y2);
            for (const auto& p : {p1, p2, p3, p4}) {
                if (points.count(p)) points.erase(p);
                else                points.insert(p);
            }
        }
        // check if the area is the same
        long long expectedArea = static_cast<long long>(X2 - X1) * (Y2 - Y1); // Cast to long long before multiplication
        if (actualArea != expectedArea) {
            return false;
        }
        // check if the number of vertices is 4
        if (points.size() != 4) {
            return false;
        }
        // check if the 4 vertices left belong to the perfect rectangle
        if (!points.count(to_string(X1) + "," + to_string(Y1))) return false;
        if (!points.count(to_string(X1) + "," + to_string(Y2))) return false;
        if (!points.count(to_string(X2) + "," + to_string(Y1))) return false;
        if (!points.count(to_string(X2) + "," + to_string(Y2))) return false;
        // if the area and vertices match, the rectangle meets the requirements
        return true;
    }
};

class Solution:
    def isRectangleCover(self, rectangles: List[List[int]]) -> bool:
        X1, Y1 = float('inf'), float('inf')
        X2, Y2 = float('-inf'), float('-inf')
        
        points = set()
        actualArea = 0
        for rect in rectangles:
            x1, y1, x2, y2 = rect
            # calculate the theoretical vertex coordinates of the perfect rectangle
            X1 = min(X1, x1)
            Y1 = min(Y1, y1)
            X2 = max(X2, x2)
            Y2 = max(Y2, y2)
            # accumulate the area of the small rectangle
            actualArea += (x2 - x1) * (y2 - y1)
            # the final vertices of the formed shape
            p1 = f"{x1},{y1}"
            p2 = f"{x1},{y2}"
            p3 = f"{x2},{y1}"
            p4 = f"{x2},{y2}"
            for p in [p1, p2, p3, p4]:
                if p in points:
                    points.remove(p)
                else:
                    points.add(p)
        # check if the area is the same
        expectedArea = (X2 - X1) * (Y2 - Y1)
        if actualArea != expectedArea:
            return False
        # check if the number of vertices is 4
        if len(points) != 4:
            return False
        # check if the 4 vertices left belong to the perfect rectangle
        if not (f"{X1},{Y1}" in points and f"{X1},{Y2}" in points and f"{X2},{Y1}" in points and f"{X2},{Y2}" in points):
            return False
        # if the area and vertices match, the rectangle meets the requirements
        return True

func isRectangleCover(rectangles [][]int) bool {
    X1, Y1 := int(^uint(0)>>1), int(^uint(0)>>1)
    X2, Y2 := -int(^uint(0)>>1)-1, -int(^uint(0)>>1)-1
    
    points := make(map[string]bool)
    actualArea := 0
    for _, rect := range rectangles {
        x1, y1, x2, y2 := rect[0], rect[1], rect[2], rect[3]
        // calculate the theoretical vertex coordinates of the perfect rectangle
        if x1 < X1 { X1 = x1 }
        if y1 < Y1 { Y1 = y1 }
        if x2 > X2 { X2 = x2 }
        if y2 > Y2 { Y2 = y2 }
        // accumulate the area of the small rectangle
        actualArea += (x2 - x1) * (y2 - y1)
        // the final vertices of the formed shape
        p1 := fmt.Sprintf("%d,%d", x1, y1)
        p2 := fmt.Sprintf("%d,%d", x1, y2)
        p3 := fmt.Sprintf("%d,%d", x2, y1)
        p4 := fmt.Sprintf("%d,%d", x2, y2)
        for _, p := range []string{p1, p2, p3, p4} {
            if points[p] {
                delete(points, p)
            } else {
                points[p] = true
            }
        }
    }
    // check if the area is the same
    expectedArea := (X2 - X1) * (Y2 - Y1)
    if actualArea != expectedArea {
        return false
    }
    // check if the number of vertices is 4
    if len(points) != 4 {
        return false
    }
    // check if the 4 vertices left belong to the perfect rectangle
    if !points[fmt.Sprintf("%d,%d", X1, Y1)] || 
       !points[fmt.Sprintf("%d,%d", X1, Y2)] || 
       !points[fmt.Sprintf("%d,%d", X2, Y1)] || 
       !points[fmt.Sprintf("%d,%d", X2, Y2)] {
        return false
    }
    // if the area and vertices match, the rectangle meets the requirements
    return true
}

var isRectangleCover = function(rectangles) {
    let X1 = Number.MAX_VALUE, Y1 = Number.MAX_VALUE;
    let X2 = Number.MIN_VALUE, Y2 = Number.MIN_VALUE;
    
    let points = new Set();
    let actualArea = 0;
    for (let rect of rectangles) {
        let x1 = rect[0], y1 = rect[1], x2 = rect[2], y2 = rect[3];
        // calculate the theoretical vertex coordinates of the perfect rectangle
        X1 = Math.min(X1, x1);
        Y1 = Math.min(Y1, y1);
        X2 = Math.max(X2, x2);
        Y2 = Math.max(Y2, y2);
        // accumulate the area of the small rectangle
        actualArea += (x2 - x1) * (y2 - y1);
        // the final vertices of the formed shape
        let p1 = x1 + "," + y1;
        let p2 = x1 + "," + y2;
        let p3 = x2 + "," + y1;
        let p4 = x2 + "," + y2;
        for (let p of [p1, p2, p3, p4]) {
            if (points.has(p)) points.delete(p);
            else                points.add(p);
        }
    }
    // check if the area is the same
    let expectedArea = (X2 - X1) * (Y2 - Y1);
    if (actualArea !== expectedArea) {
        return false;
    }
    // check if the number of vertices is 4
    if (points.size !== 4) {
        return false;
    }
    // check if the 4 vertices left belong to the perfect rectangle
    if (!points.has(X1 + "," + Y1)) return false;
    if (!points.has(X1 + "," + Y2)) return false;
    if (!points.has(X2 + "," + Y1)) return false;
    if (!points.has(X2 + "," + Y2)) return false;
    // if the area and vertices match, the rectangle meets the requirements
    return true;
};

This is the final solution. It checks two things:

1. Area: Use the theoretical coordinates of the perfect rectangle to calculate its theoretical area, then compare it with the total area of all small rectangles in rectangles.

2. Vertices: The points set should have only 4 points left, and these points must be exactly the four theoretical corners of the perfect rectangle.