Pancake Sorting Algorithm

LeetCode Problem 969 "Pancake Sorting" is an interesting real-world problem: Imagine you have n pancakes of different sizes on a plate. Using a spatula, how can you flip the pancakes a few times to sort them by size (smallest on top, largest on bottom)?

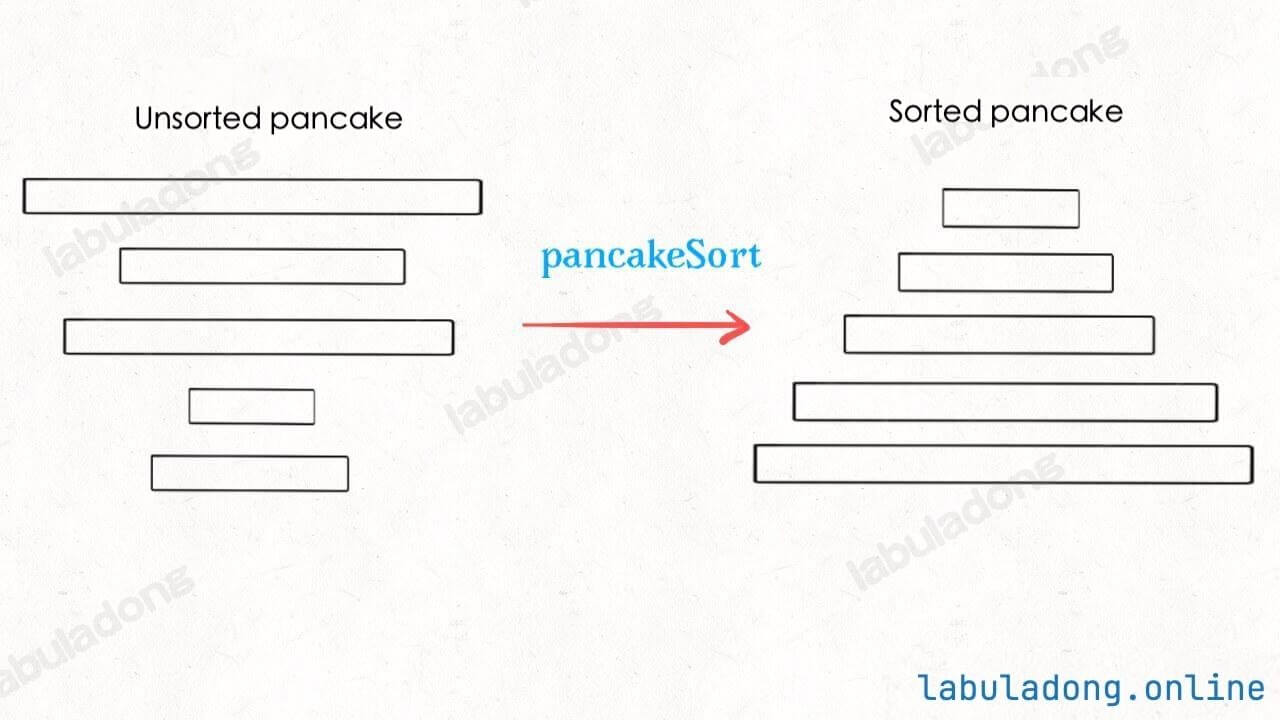
Think of flipping a stack of pancakes with a spatula. There is a rule: each time, you can only flip the top few pancakes.

Our task is: How can we use an algorithm to find a sequence of flips to make the pancake stack sorted?

First, we need to model the problem. We use an array to represent the pancake stack:

Input: arr = [3,2,4,1]
Output: [4,2,4,3]
Explanation: 
We perform 4 pancake flips, with k values 4, 2, 4, and 3.
Starting state: arr = [3, 2, 4, 1]
After 1st flip (k = 4): arr = [1, 4, 2, 3]
After 2nd flip (k = 2): arr = [4, 1, 2, 3]
After 3rd flip (k = 4): arr = [3, 2, 1, 4]
After 4th flip (k = 3): arr = [1, 2, 3, 4], which is sorted.

Input: arr = [1,2,3]
Output: []
Explanation: The input is already sorted, so there is no need to flip anything.
Note that other answers, such as [3, 3], would also be accepted.

How do we solve this problem? Like in the article Recursively Reverse Part of a Linked List, we need to use recursion.

1. Idea Analysis

Why does this problem have the property of recursion? For example, we can make a function like this:

// cakes is a pile of pancakes, the function will sort the first n pancakes
void sort(int[] cakes, int n);

// cakes is a pile of pancakes, the function will sort the first n pancakes
void sort(int cakes[], int n);

# cakes is a pile of pancakes, the function will sort the first n pancakes
def sort(cakes: List[int], n: int):

// cakes is a pile of pancakes, the function will sort the first n pancakes
func sort(cakes []int, n int) {}

// cakes is a pile of pancakes, the function will sort the first n pancakes
var sort = function(cakes, n) {
};

If we find the largest pancake among the first n pancakes, and flip it to the bottom:

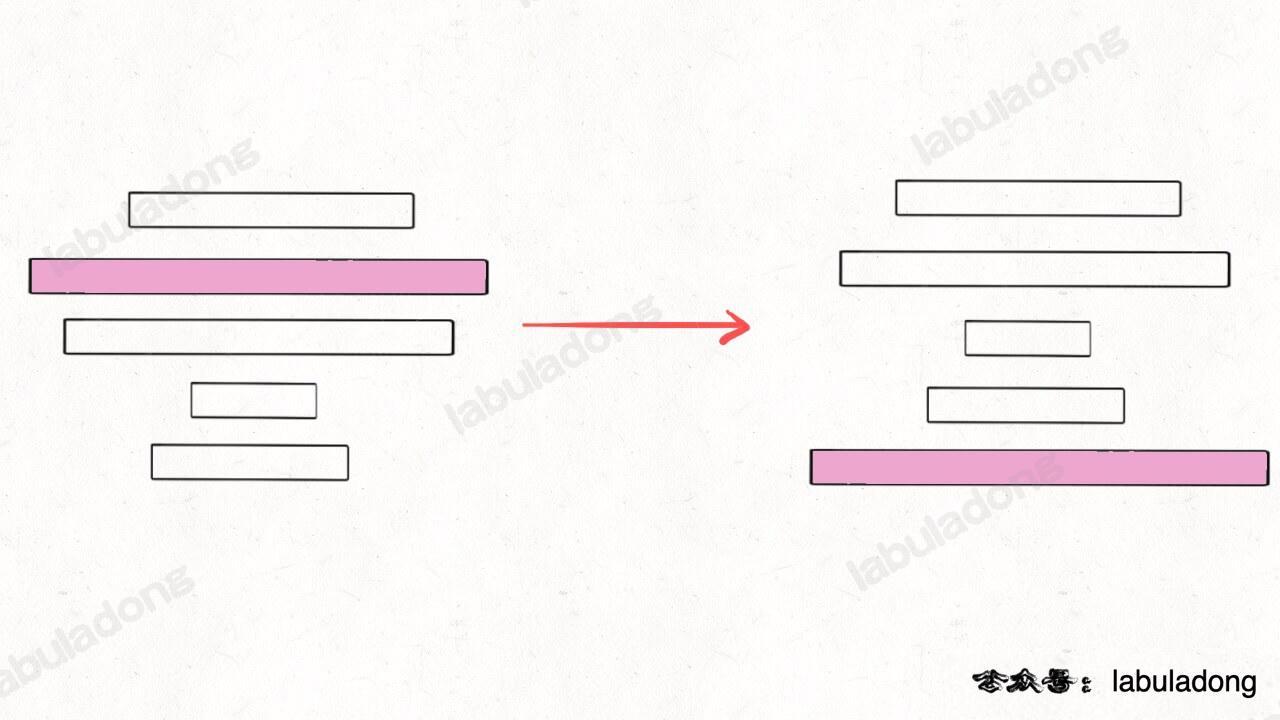
Now the problem size is smaller, so we can recursively call pancakeSort(A, n-1):

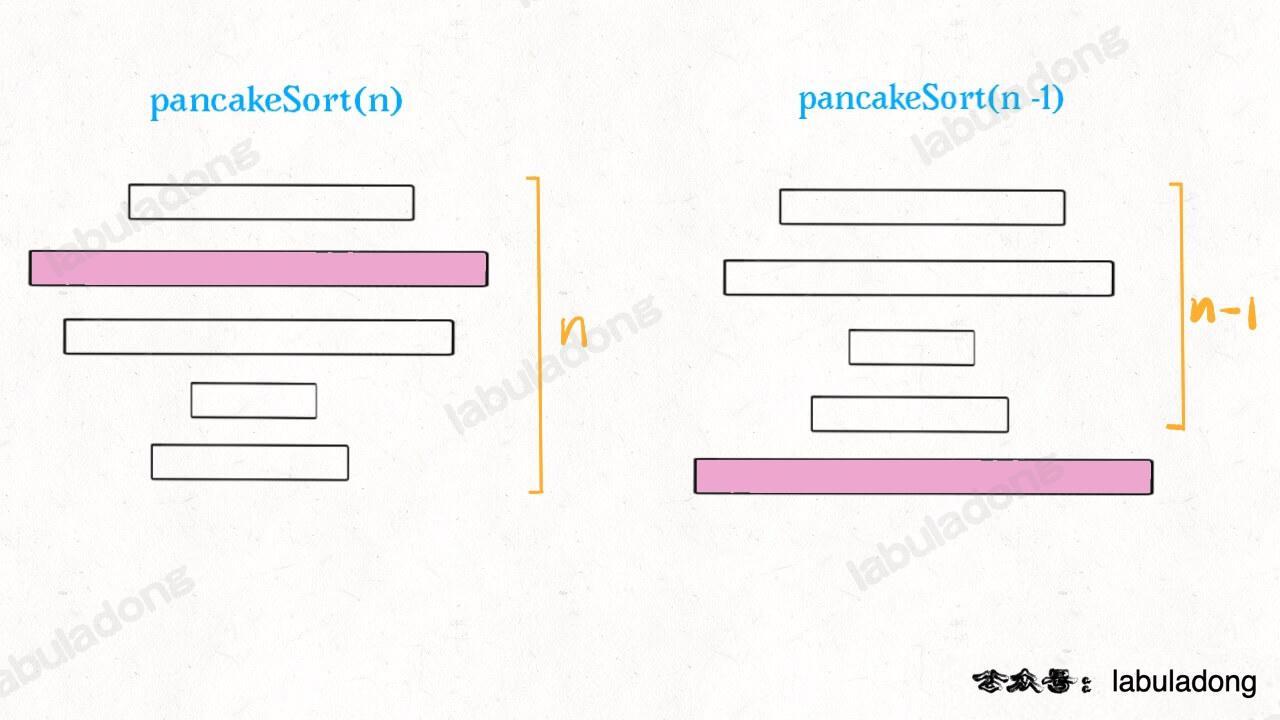
Next, for these n - 1 pancakes, how to sort them? Again, find the largest, put it at the bottom, and call pancakeSort(A, n-1-1)...

You see, this is recursion. To summarize:

1. Find the largest pancake among the n pancakes.

2. Move this largest pancake to the bottom.

3. Recursively call pancakeSort(A, n - 1).

Base case: When n == 1, there is only one pancake, so no flips are needed.

Now, one last question: How do we move a certain pancake to the bottom?

It's simple. For example, if the 3rd pancake is the largest and you want to move it to the bottom (the nth position):

1. Use the spatula to flip the top 3 pancakes. Now the largest is at the top.

2. Flip the top n pancakes. Now the largest is at the bottom.

With these two steps, you can write the solution. The problem also asks us to return the flip operation sequence. We just need to record each flip.

2. Code Implementation

Just write the above idea in code. Note: array index starts from 0, but the answer should use 1-based indices.

class Solution {
    // record the sequence of flip operations
    LinkedList<Integer> res = new LinkedList<>();

    public List<Integer> pancakeSort(int[] cakes) {
        sort(cakes, cakes.length);
        return res;
    }

    void sort(int[] cakes, int n) {
        // base case
        if (n == 1) return;

        // find the index of the largest pancake
        int maxCake = 0;
        int maxCakeIndex = 0;
        for (int i = 0; i < n; i++)
            if (cakes[i] > maxCake) {
                maxCakeIndex = i;
                maxCake = cakes[i];
            }

        // first flip, move the largest pancake to the top
        reverse(cakes, 0, maxCakeIndex);
        res.add(maxCakeIndex + 1);
        // second flip, move the largest pancake to the bottom
        reverse(cakes, 0, n - 1);
        res.add(n);

        // recursive call
        sort(cakes, n - 1);

    }

    void reverse(int[] arr, int i, int j) {
        while (i < j) {
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
            i++;
            j--;
        }
    }
}

class Solution {
public:
    // record the sequence of reversal operations
    vector<int> res;

    vector<int> pancakeSort(vector<int>& cakes) {
        sort(cakes, cakes.size());
        return res;
    }

    void sort(vector<int>& cakes, int n) {
        // base case
        if (n == 1) return;

        // find the index of the largest cake
        int maxCake = 0;
        int maxCakeIndex = 0;
        for (int i = 0; i < n; i++)
            if (cakes[i] > maxCake) {
                maxCakeIndex = i;
                maxCake = cakes[i];
            }

        // first reversal, flip the largest cake to the top
        reverse(cakes, 0, maxCakeIndex);
        res.push_back(maxCakeIndex + 1);
        // second reversal, flip the largest cake to the bottom
        reverse(cakes, 0, n - 1);
        res.push_back(n);

        // recursive call
        sort(cakes, n - 1);
    }

    void reverse(vector<int>& arr, int i, int j) {
        while (i < j) {
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
            i++; j--;
        }
    }
};

from typing import List

class Solution:
    def pancakeSort(self, cakes: List[int]) -> List[int]:
        # record the sequence of reversal operations
        self.res = []
        self.sort(cakes, len(cakes))
        return self.res
    
    def sort(self, cakes: List[int], n: int) -> None:
        # base case
        if n == 1:
            return
        # find the index of the largest cake
        max_cake = 0
        max_cake_index = 0
        for i in range(n):
            if cakes[i] > max_cake:
                max_cake_index = i
                max_cake = cakes[i]
        # first reversal, flip the largest cake to the top
        self.reverse(cakes, 0, max_cake_index)
        self.res.append(max_cake_index + 1)
        # second reversal, flip the largest cake to the bottom
        self.reverse(cakes, 0, n - 1)
        self.res.append(n)

        # recursive call
        self.sort(cakes, n - 1)
        
    def reverse(self, arr: List[int], i: int, j: int) -> None:
        while i < j:
            arr[i], arr[j] = arr[j], arr[i]
            i += 1
            j -= 1

func pancakeSort(cakes []int) []int {
    res := []int{}
    sort(cakes, len(cakes), &res)
    return res
}

func sort(cakes []int, n int, res *[]int) {
    // base case
    if n == 1 {
        return
    }

    // find the index of the largest cake
    maxCake := 0
    maxCakeIndex := 0
    for i := 0; i < n; i++ {
        if cakes[i] > maxCake {
            maxCakeIndex = i
            maxCake = cakes[i]
        }
    }

    // first flip, flip the largest cake to the top
    reverse(cakes, 0, maxCakeIndex)
    *res = append(*res, maxCakeIndex+1)
    
    // second flip, flip the largest cake to the bottom
    reverse(cakes, 0, n-1)
    *res = append(*res, n)

    // recursive call
    sort(cakes, n-1, res)
}

func reverse(arr []int, i int, j int) {
    for i < j {
        arr[i], arr[j] = arr[j], arr[i]
        i++
        j--
    }
}

var pancakeSort = function(cakes) {
    // record the sequence of flip operations
    const res = [];

    const sort = function(cakes, n) {
        // base case
        if (n == 1) return;
        
        // find the index of the largest pancake
        let maxCake = 0;
        let maxCakeIndex = 0;
        for (let i = 0; i < n; i++)
            if (cakes[i] > maxCake) {
                maxCakeIndex = i;
                maxCake = cakes[i];
            }
        
        // first flip, flip the largest pancake to the top
        reverse(cakes, 0, maxCakeIndex);
        res.push(maxCakeIndex + 1);
        // second flip, flip the largest pancake to the bottom
        reverse(cakes, 0, n - 1);
        res.push(n);

        // recursive call
        sort(cakes, n - 1);
    };

    const reverse = function(arr, i, j) {
        while (i < j) {
            var temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
            i++; j--;
        }
    };

    sort(cakes, cakes.length);
    return res;
};

With the explanation above, the code should be clear.

The time complexity is easy to calculate. There are n recursive calls, and each call has a for loop of O(n), so total time complexity is O(n^2).

Finally, let's think about a question: In this solution, the length of the flip sequence is 2(n - 1), because each recursion does 2 flips, and there are n layers of recursion. But the base case does not flip, so the total number is 2(n - 1).

Clearly, this is not the optimal (shortest) sequence. For example, with pancakes [3,2,4,1], our algorithm gives flips [3,4,2,3,1,2]. But the shortest flip sequence is [2,3,4]:

Start:        [3,2,4,1]
Flip top 2:   [2,3,4,1]
Flip top 3:   [4,3,2,1]
Flip top 4:   [1,2,3,4]

If you are asked to find the shortest flip sequence to sort the pancakes, how would you solve it? What is the core idea to find the optimal solution? What algorithm should you use? Feel free to share your thoughts.