Searching for a Celebrity

Today, we will discuss the classic "Celebrity Problem":

You are given the social relationships of n people (you know whether any two people know each other), and you need to identify the "celebrity" among these people.

The so-called "celebrity" has two conditions:

1. Everyone else knows the "celebrity."

2. The "celebrity" does not know anyone else.

This is an algorithm problem related to graph theory, as social relationships can essentially be abstracted into a graph.

If each person is regarded as a node in the graph, the "knows" relationship is considered a directed edge between nodes, then a celebrity is a special node in this graph:

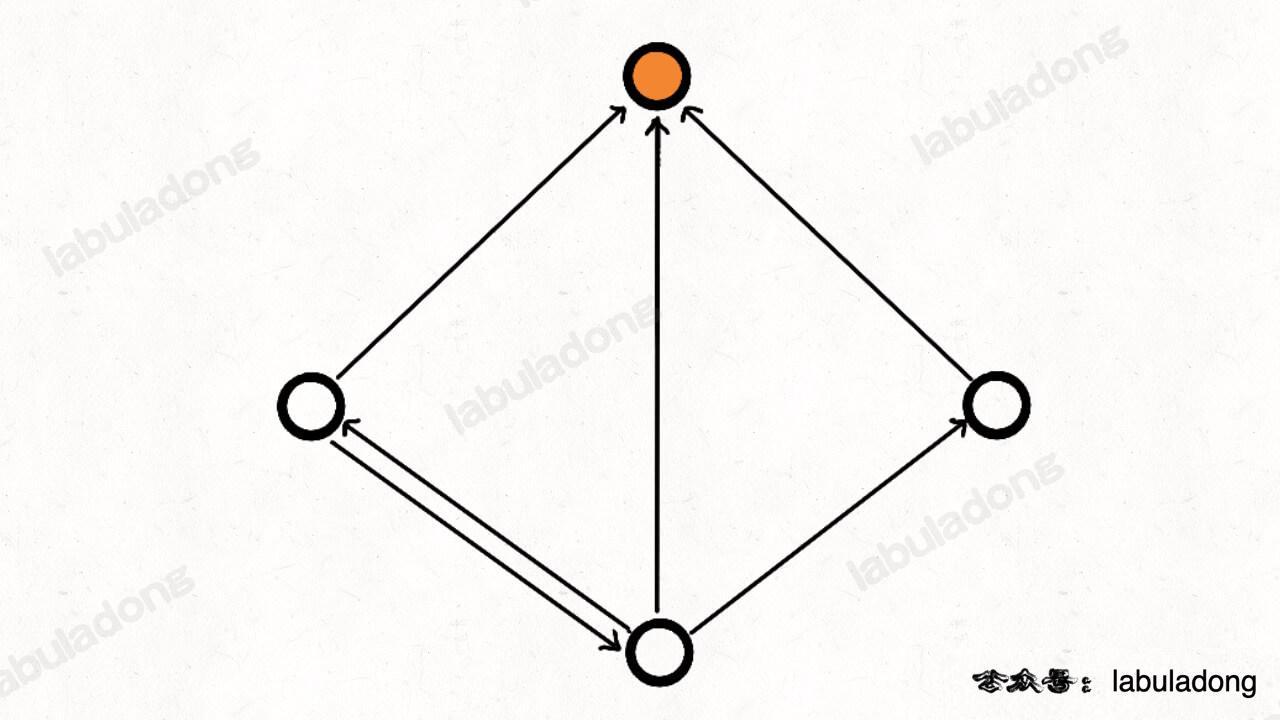
This node has no outgoing directed edges to other nodes; and all other nodes have a directed edge pointing to this node.

In more technical terms, the out-degree of the celebrity node is 0, and the in-degree is n - 1.

So, how are the social relationships of these n people represented?

In the previous Graph Theory Basics, it was mentioned that there are two storage forms for graphs: adjacency list and adjacency matrix. The main advantage of an adjacency list is saving storage space, while the main advantage of an adjacency matrix is quickly determining whether two nodes are adjacent.

For the celebrity problem, it is clear that we often need to determine whether two people know each other, which means whether two nodes are adjacent. Therefore, we can use an adjacency matrix to represent the social relationships between people.

Thus, the celebrity problem can be described in algorithmic form as follows:

You are given an input of a n x n two-dimensional array (adjacency matrix) graph representing a graph with n nodes, where each person is a node in the graph, numbered from 0 to n - 1.

If graph[i][j] == 1, it means person i knows person j. If graph[i][j] == 0, it means person i does not know person j.

Given this graph representing the relationships between people, please determine if there exists a "celebrity" among these n people.

If a celebrity exists, the algorithm returns the index of this celebrity. If not, the algorithm returns -1.

The function signature is as follows:

int findCelebrity(int[][] graph);

int findCelebrity(vector<vector<int>>& graph);

def findCelebrity(graph: List[List[int]]) -> int:

func findCelebrity(graph [][]int) int {}

var findCelebrity = function(graph) { }

For example, if the input adjacency matrix looks like this:

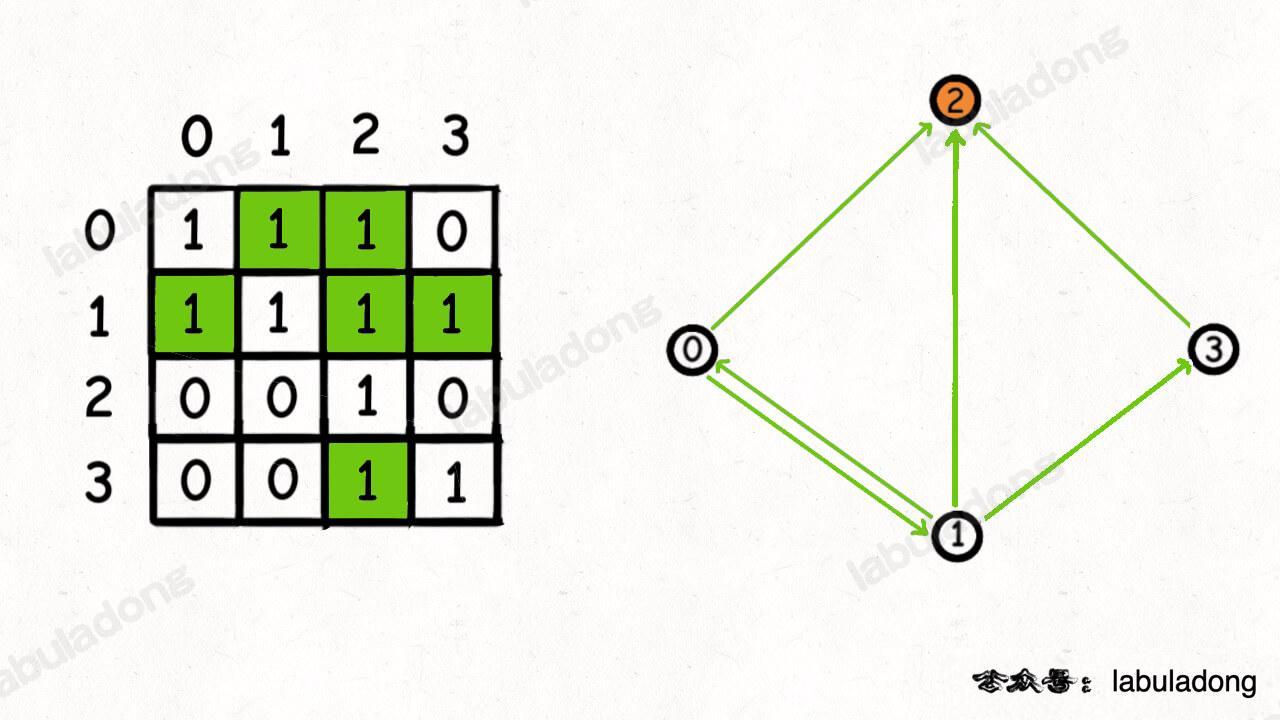
Then the algorithm should return 2.

LeetCode Problem 277 "Find the Celebrity" is a classic example of this problem. However, instead of directly providing you with the adjacency matrix, you are only given the total number of people n and an API knows to query the social relationship between individuals:

// can be called directly, returns whether i knows j
boolean knows(int i, int j);

// please implement: return the number of the "celebrity"
int findCelebrity(int n) {
    // todo
}

// can be called directly, returns whether i knows j
bool knows(int i, int j);

// please implement: return the number of the "celebrity"
int findCelebrity(int n) {
    // todo
}

# Can be called directly, returns whether i knows j
def knows(i: int, j: int) -> bool:
    pass

# Please implement: return the number of the 'celebrity'
def findCelebrity(n: int) -> int:
    # todo

// can be called directly, returns whether i knows j
func knows(i int, j int) bool {}

// please implement: return the number of the "celebrity"
func findCelebrity(n int) int {
    // todo
}

// can be called directly, returns whether i knows j
var knows = function(i, j) {};

// please implement: return the number of the 'celebrity'
var findCelebrity = function(n) {
    // todo
};

Clearly, the knows API essentially accesses an adjacency matrix. For simplicity, we will discuss this classic problem following the format of LeetCode problems.

Brute Force Solution

We can quickly come up with a simple and straightforward algorithm:

class Solution extends Relation {
    public int findCelebrity(int n) {
        for (int cand = 0; cand < n; cand++) {
            int other;
            for (other = 0; other < n; other++) {
                if (cand == other) continue;
                // ensure that everyone else knows cand, and cand does not know anyone else
                // otherwise, cand cannot be the celebrity
                if (knows(cand, other) || !knows(other, cand)) {
                    break;
                }
            }
            if (other == n) {
                // found the celebrity
                return cand;
            }
        }
        // no one fits the characteristics of a celebrity
        return -1;
    }
}

class Solution {
public:
    int findCelebrity(int n) {
        for (int cand = 0; cand < n; cand++) {
            int other;
            for (other = 0; other < n; other++) {
                if (cand == other) continue;
                // ensure everyone else knows cand, and cand does not know anyone else
                // otherwise, cand cannot be the celebrity
                if (knows(cand, other) || !knows(other, cand)) {
                    break;
                }
            }
            if (other == n) {
                // found the celebrity
                return cand;
            }
        }
        // no one matches the characteristics of a celebrity
        return -1;
    }
};

class Solution:
    def findCelebrity(self, n: int) -> int:
        for cand in range(n):
            other = 0
            # ensure everyone else knows cand, and cand does not know anyone else
            # otherwise, cand cannot be the celebrity
            while other < n:
                if cand == other:
                    other += 1
                    continue
                if knows(cand, other) or not knows(other, cand):
                    break
                other += 1
            if other == n:
                # found the celebrity
                return cand
        # no one fits the characteristics of a celebrity
        return -1

func solution(knows func(a int, b int) bool) func(n int) int {
    return func(n int) int {
        for cand := 0; cand < n; cand++ {
            var other int
            for other = 0; other < n; other++ {
                if cand == other {
                    continue
                }
                // ensure everyone else knows cand, and cand does not know anyone else
                // otherwise cand cannot be the celebrity
                if knows(cand, other) || !knows(other, cand) {
                    break
                }
            }
            if other == n {
                // found the celebrity
                return cand
            }
        }
        // no one has the characteristics of a celebrity
        return -1
    }
}

var solution = function(knows) {
    return function(n) {
        for (let cand = 0; cand < n; cand++) {
            let other;
            for (other = 0; other < n; other++) {
                if (cand === other) {
                    continue;
                }
                // ensure everyone else knows cand, and cand does not know anyone else
                // otherwise cand cannot be the celebrity
                if (knows(cand, other) || !knows(other, cand)) {
                    break;
                }
            }
            if (other === n) {
                // found the celebrity
                return cand;
            }
        }
        // no one matches the celebrity characteristics
        return -1;
    };
};

cand is short for "candidate." Our brute-force algorithm starts from the beginning, treating everyone as a candidate and checking if they meet the "celebrity" criteria.

As mentioned earlier, the knows function essentially accesses a two-dimensional adjacency matrix, with a time complexity of O(1) per call. Therefore, the overall worst-case time complexity of this brute-force solution is O(N^2).

Is there a smarter way to optimize the time complexity? Actually, there is room for optimization. Think about where the most time-consuming part is.

For each candidate cand, we use an inner for loop to determine if cand meets the "celebrity" criteria.

This inner for loop seems inefficient. While checking if someone is a "celebrity" requires a for loop, determining that someone is not a "celebrity" doesn't need to be so complicated.

Because the definition of a "celebrity" ensures uniqueness, we can use the process of elimination to first exclude those who are obviously not "celebrities," thereby avoiding nested for loops and reducing the time complexity.

Optimized Solution

Let me repeat the definition of a "celebrity":

1. Everyone else knows the celebrity.

2. The celebrity knows no one else.

This definition is interesting because it ensures that there can be at most one celebrity in the group.

This is easy to understand: if there are two people who are both celebrities, these two definitions would contradict each other.

In other words, by observing the relationship between any two candidates, I can determine that one of them is not a celebrity and exclude them.

As for whether the other candidate is a celebrity, simply looking at the relationship between two people cannot confirm this, but that's not important. What matters is excluding a candidate who is definitely not a celebrity, thus narrowing down the possibilities.

This is the core of the optimization and can be somewhat difficult to understand, so let's first discuss why observing the relationship between any two candidates allows us to exclude one of them.

Think about it, what can the relationship between two people be like?

There are essentially four possibilities: I know you but you don't know me, you know me but I don't know you, we both know each other, or neither of us knows each other.

If you consider people as nodes, with red directed edges indicating not knowing and green directed edges indicating knowing, then the relationships between two people can be one of the following four scenarios:

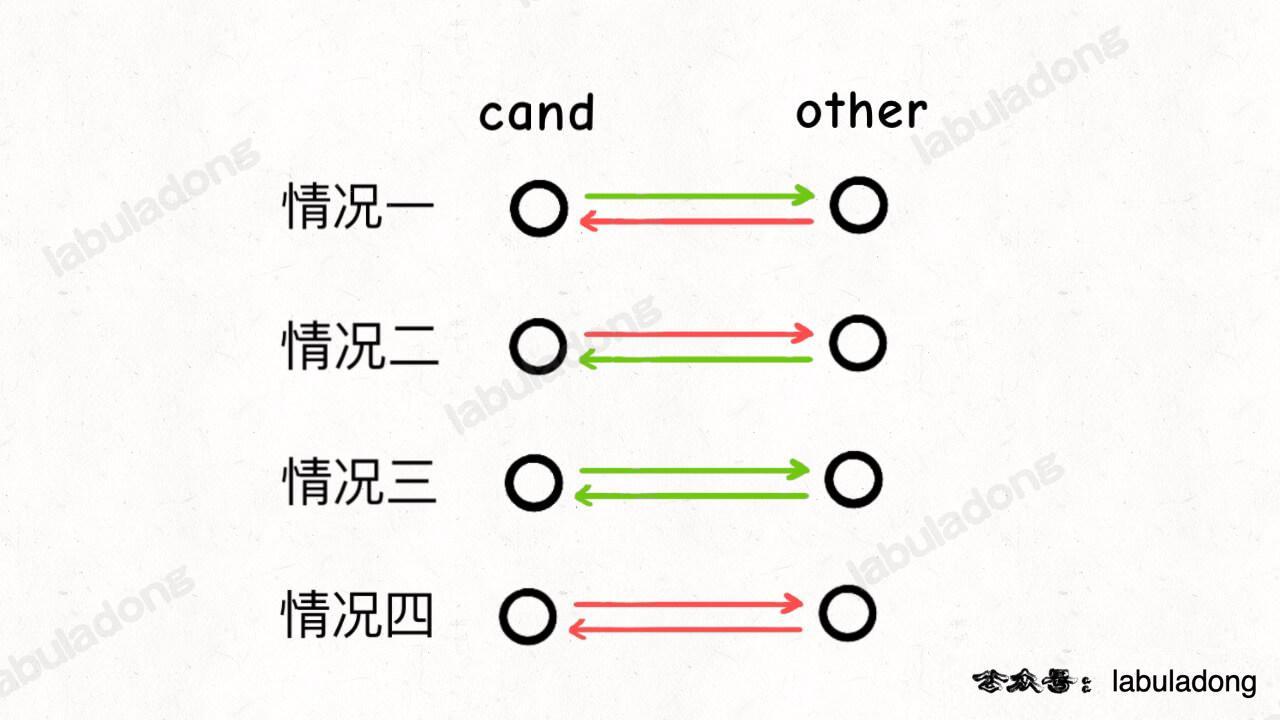
Let's assume these two people are numbered cand and other, and analyze each scenario to see how to exclude one person.

In the first scenario, cand knows other, so cand is definitely not a celebrity and can be excluded because a celebrity cannot know others.

In the second scenario, other knows cand, so other is definitely not a celebrity and can be excluded.

In the third scenario, they know each other, so neither is a celebrity and either can be excluded.

In the fourth scenario, neither knows the other, so neither is a celebrity and either can be excluded. A celebrity should be known by everyone else.

In summary, by observing the relationship between any two people, at least one person can be determined not to be a celebrity. The judgment for each scenario can be represented with the following code:

if (knows(cand, other) || !knows(other, cand)) {
    // cand cannot be a celebrity
} else {
    // other cannot be a celebrity
}

if (knows(cand, other) || !knows(other, cand)) {
    // cand cannot be a celebrity
}
else {
    // other cannot be a celebrity
}

if knows(cand, other) or not knows(other, cand):
    # cand cannot be the celebrity
else:
    # other cannot be the celebrity

if knows(cand, other) || !knows(other, cand) {
    // cand cannot be the celebrity
} else {
    // other cannot be the celebrity
}

if (knows(cand, other) || !knows(other, cand)) {
    // cand cannot be a celebrity
} else {
    // other cannot be a celebrity
}

If you can understand this characteristic, writing an optimized solution becomes simple.

We can continuously select two candidates and eliminate one until only one candidate remains. At that point, we use a for loop to determine if this candidate is truly a "celebrity".

Here is the complete code for this approach:

class Solution extends Relation {
    public int findCelebrity(int n) {
        if (n == 1) return 0;
        // put all candidates into the queue
        LinkedList<Integer> q = new LinkedList<>();
        for (int i = 0; i < n; i++) {
            q.addLast(i);
        }
        // keep eliminating until only one candidate is left
        while (q.size() >= 2) {
            // each time take out two candidates and eliminate one
            int cand = q.removeFirst();
            int other = q.removeFirst();
            if (knows(cand, other) || !knows(other, cand)) {
                // cand cannot be the celebrity, eliminate and let other rejoin the queue
                q.addFirst(other);
            } else {
                // other cannot be the celebrity, eliminate and let cand rejoin the queue
                q.addFirst(cand);
            }
        }

        // now there is only one candidate left, determine if he is really the celebrity
        int cand = q.removeFirst();
        for (int other = 0; other < n; other++) {
            if (other == cand) {
                continue;
            }
            // ensure that everyone else knows cand, and cand does not know anyone else
            if (!knows(other, cand) || knows(cand, other)) {
                return -1;
            }
        }
        // cand is the celebrity
        return cand;
    }
}

class Solution {
public:
    int findCelebrity(int n) {
        if (n == 1) return 0;
        // put all candidates into the queue
        queue<int> q;
        for (int i = 0; i < n; i++) {
            q.push(i);
        }
        // keep eliminating until only one candidate is left
        while (q.size() >= 2) {
            // each time take out two candidates and eliminate one
            int cand = q.front();
            q.pop();
            int other = q.front();
            q.pop();
            if (knows(cand, other) || !knows(other, cand)) {
                // cand cannot be the celebrity, eliminate and let other rejoin the queue
                q.push(other);
            } else {
                // other cannot be the celebrity, eliminate and let cand rejoin the queue
                q.push(cand);
            }
        }

        // now that only one candidate is left, determine if he is really the celebrity
        int cand = q.front();
        for (int other = 0; other < n; other++) {
            if (other == cand) {
                continue;
            }
            // ensure that everyone else knows cand, and cand does not know anyone else
            if (!knows(other, cand) || knows(cand, other)) {
                return -1;
            }
        }
        // cand is the celebrity
        return cand;
    }
};

class Solution:
    def findCelebrity(self, n: int) -> int:
        if n == 1:
            return 0
        # put all candidates into the queue
        q = collections.deque(range(n))
        # keep eliminating until only one candidate is left
        while len(q) >= 2:
            # each time take out two candidates and eliminate one
            cand = q.popleft()
            other = q.popleft()
            if knows(cand, other) or not knows(other, cand):
                # cand cannot be the celebrity, eliminate and let other rejoin the queue
                q.appendleft(other)
            else:
                # other cannot be the celebrity, eliminate and let cand rejoin the queue
                q.appendleft(cand)

        # now only one candidate is left, determine if he is really the celebrity
        cand = q.popleft()
        for other in range(n):
            if other == cand:
                continue
            # ensure everyone else knows cand, and cand does not know any other person
            if not knows(other, cand) or knows(cand, other):
                return -1
        # cand is the celebrity
        return cand

func solution(knows func(a int, b int) bool) func(n int) int {
    return func(n int) int {
        if n == 1 {
            return 0
        }
        // put all candidates into the queue
        q := make([]int, n)
        for i := 0; i < n; i++ {
            q[i] = i
        }
        // keep eliminating until there is only one candidate left in the loop
        for len(q) >= 2 {
            // each time take out two candidates and eliminate one
            cand := q[0]
            q = q[1:]
            other := q[0]
            q = q[1:]
            if knows(cand, other) || !knows(other, cand) {
                // cand cannot be the celebrity, eliminate and let other rejoin the queue
                q = append([]int{other}, q...)
            } else {
                // other cannot be the celebrity, eliminate and let cand rejoin the queue
                q = append([]int{cand}, q...)
            }
        }

        // now that there is only one candidate left, determine if he is really a celebrity
        cand := q[0]
        for other := 0; other < n; other++ {
            if other == cand {
                continue
            }
            // ensure that everyone else knows cand, and cand does not know any other person
            if !knows(other, cand) || knows(cand, other) {
                return -1
            }
        }
        // cand is the celebrity
        return cand
    }
}

var solution = function(knows) {
    return function(n) {
        if (n === 1) {
            return 0;
        }
        // put all candidates into the queue
        let q = Array.from({ length: n }, (_, i) => i);
        // keep eliminating until only one candidate is left
        while (q.length >= 2) {
            // each time take out two candidates and eliminate one
            let cand = q.shift();
            let other = q.shift();
            if (knows(cand, other) || !knows(other, cand)) {
                // cand cannot be the celebrity, eliminate and let other rejoin the queue
                q.unshift(other);
            } else {
                // other cannot be the celebrity, eliminate and let cand rejoin the queue
                q.unshift(cand);
            }
        }

        // now there is only one candidate left, determine if he is really a celebrity
        let cand = q.shift();
        for (let other = 0; other < n; other++) {
            if (other === cand) {
                continue;
            }
            // make sure everyone else knows cand, and cand does not know anyone else
            if (!knows(other, cand) || knows(cand, other)) {
                return -1;
            }
        }
        // cand is the celebrity
        return cand;
    };
};

This algorithm avoids nested for loops, reducing the time complexity to O(N). However, it introduces a queue to store the set of candidates, using O(N) space complexity.

Can we further optimize to reduce the space complexity as well?

Final Solution

If you understand the optimization method described above, you can actually solve this problem without using extra space. The code is as follows:

class Solution extends Relation {
    public int findCelebrity(int n) {
        int cand = 0;
        for (int other = 1; other < n; other++) {
            if (!knows(other, cand) || knows(cand, other)) {
                // cand cannot be a celebrity, eliminate
                // assume other is a celebrity
                cand = other;
            } else {
                // other cannot be a celebrity, eliminate
                // do nothing, continue to assume cand is a celebrity
            }
        }

        // now cand is the last one remaining after
        // elimination, but it's not guaranteed to be a
        for (int other = 0; other < n; other++) {
            if (cand == other) continue;
            // need to ensure everyone else knows cand, and cand does not know any other person
            if (!knows(other, cand) || knows(cand, other)) {
                return -1;
            }
        }

        return cand;
    }
}

class Solution {
public:
    int findCelebrity(int n) {
        int cand = 0;
        for (int other = 1; other < n; other++) {
            if (!knows(other, cand) || knows(cand, other)) {
                // cand cannot be the celebrity, eliminate
                // assume other is the celebrity
                cand = other;
            } else {
                // other cannot be the celebrity, eliminate
                // do nothing, continue to assume cand is the celebrity
            }
        }

        // now cand is the last remaining candidate, but it's not guaranteed to be the celebrity
        for (int other = 0; other < n; other++) {
            if (cand == other) continue;
            // need to ensure everyone else knows cand, and cand does not know any other person
            if (!knows(other, cand) || knows(cand, other)) {
                return -1;
            }
        }

        return cand;
    }
};

class Solution:
    def findCelebrity(self, n: int) -> int:
        cand = 0
        for other in range(1, n):
            if not knows(other, cand) or knows(cand, other):
                # cand can't be the celebrity, eliminate
                # assume other is the celebrity
                cand = other
            else:
                # other can't be the celebrity, eliminate
                # do nothing, continue to assume cand is the celebrity
                pass

        # now cand is the last one remaining after
        # elimination, but it's not guaranteed to be the
        for other in range(n):
            if cand == other:
                continue
            # need to ensure everyone else knows cand, and cand doesn't know any other person
            if not knows(other, cand) or knows(cand, other):
                return -1

        return cand

func solution(knows func(a int, b int) bool) func(n int) int {
    return func(n int) int {
        cand := 0
        for other := 1; other < n; other++ {
            if !knows(other, cand) || knows(cand, other) {
                // cand cannot be the celebrity, eliminate
                // assume other is the celebrity
                cand = other
            } else {
                // other cannot be the celebrity, eliminate
                // do nothing, continue to assume cand is the celebrity
            }
        }

        // now cand is the last one remaining after
        // elimination, but it's not guaranteed to be the
        for other := 0; other < n; other++ {
            if cand == other {
                continue
            }
            // need to ensure everyone else knows cand, and cand does not know any other person
            if !knows(other, cand) || knows(cand, other) {
                return -1
            }
        }

        return cand
    }
}

var solution = function(knows) {
    return function(n) {
        let cand = 0;
        for (let other = 1; other < n; other++) {
            if (!knows(other, cand) || knows(cand, other)) {
                // cand cannot be the celebrity, eliminate
                // assume other is the celebrity
                cand = other;
            } else {
                // other cannot be the celebrity, eliminate
                // do nothing, continue to assume cand is the celebrity
            }
        }

        // now cand is the last remaining after
        // elimination, but it's not guaranteed to be
        for (let other = 0; other < n; other++) {
            if (cand === other) {
                continue;
            }
            // need to ensure everyone else knows cand, and cand does not know anyone else
            if (!knows(other, cand) || knows(cand, other)) {
                return -1;
            }
        }

        return cand;
    };
};

Our previous solution used a LinkedList to act as a queue for storing the set of candidates. This optimized solution uses the alternating changes between other and cand to simulate our previous queue operations, avoiding the use of extra storage space.

Now, the solution to the celebrity problem has a time complexity of O(N) and a space complexity of O(1), making it the optimal solution.