Designing an Exam Room Algorithm

labuladongOriginalAbout 1731 words

This article will resolve

LeetCode	Difficulty
855. Exam Room	🟠

This article discusses LeetCode Problem 855, "Exam Room", which is interesting and requires a certain level of skill. Unlike algorithms like dynamic programming that test your intelligence, this problem tests your understanding of common data structures and your coding skills.

Let's describe the problem: Assume there is an exam room with a row of N seats, indexed from [0..N-1]. Students will gradually enter the exam room for their test and may leave at any time.

As the examiner, you need to arrange the students' seats to ensure: Whenever a student enters, you maximize the distance between them and the nearest other person; if there are multiple such seats, place them in the seat with the smallest index. This reflects real-world situations, doesn't it?

So, please implement a class like the one below:

class ExamRoom {
    // constructor, passing the total number of seats N
    public ExamRoom(int N);
    // a student comes, return the seat assigned to him
    public int seat();
    // the student sitting at position p leaves
    // it can be assumed that position p is definitely occupied by a student
    public void leave(int p);
}

For example, consider an exam room with 5 seats, indexed [0..4]:

When the first student enters (calling seat()), they can sit anywhere, but should be assigned the smallest index, which is position 0.

When the second student enters (calling seat() again), they should sit as far away as possible from others, which means position 4.

The third student should also sit as far away as possible from others, ideally in the middle, which is seat 2.

If another student enters, they can sit in either seat 1 or 3, but the smaller index, 1, is chosen.

And so on.

The situation described does not involve calling the leave function, but the pattern is clear:

If we consider each pair of adjacent students as endpoints of a segment, the newly seated student should find the longest segment and "bisect" it, taking the midpoint as their seat. The leave(p) function essentially removes the endpoint p, merging two adjacent segments into one.

The core idea is straightforward, right? This problem essentially tests your understanding of data structures. What data structure would you use to implement this logic?

I. Thought Process

Following this idea, we first need to abstract the students in the classroom as segments, which can be simply represented by an array of size 2.

Additionally, since we need to find the "longest" segment, and also add and remove segments, an ordered data structure is necessary.

Whenever a dynamic process requires finding extreme values, an ordered data structure is essential. Common choices are binary heaps and balanced binary search trees.

The priority queue implemented by a binary heap has a time complexity of O(logN) for extracting extreme values, but can only delete the maximum value. Balanced binary trees can extract extreme values and modify or delete any value, all with a time complexity of O(logN).

In conclusion, a binary heap cannot support the leave operation, so a balanced binary tree should be used. Here, we use Java's TreeSet, an ordered data structure maintained by a red-black tree.

It's worth mentioning that when thinking about a set (Set) or a map (Map), some may instinctively think of a hash set (HashSet) or hash map (HashMap), which is somewhat misguided.

This is because hash sets/maps are implemented with hash functions and arrays, featuring unordered traversal but high operational efficiency with a time complexity of O(1).

Sets/maps can also rely on other underlying data structures, commonly red-black trees (a type of balanced binary search tree), which automatically maintain element order with an operational efficiency of O(logN). These are generally referred to as "ordered sets/maps."

The TreeSet we use is an ordered set, aimed at maintaining the order of segment lengths, enabling quick searches for the longest segment, and fast insertion and deletion.

II. Simplifying the Problem

Initially, if there are multiple seat options, we need to choose the seat with the smallest index, right? Let's first simplify the problem by ignoring this requirement temporarily, implementing the above logic.

This problem also employs a common programming technique: using a "virtual segment" to correctly start the algorithm, similar to how linked list algorithms use a "dummy head node."

class ExamRoom {
    // map endpoint p to the segment with p as the left endpoint
    private Map<Integer, int[]> startMap;
    // map endpoint p to the segment with p as the right endpoint
    private Map<Integer, int[]> endMap;
    // store all segments in ascending order of their length
    private TreeSet<int[]> pq;
    private int N;

    public ExamRoom(int N) {
        this.N = N;
        startMap = new HashMap<>();
        endMap = new HashMap<>();
        pq = new TreeSet<>((a, b) -> {
            // calculate the lengths of two segments
            int distA = distance(a);
            int distB = distance(b);
            // longer lengths are considered greater, placed at the back
            return distA - distB;
        });
        // initially put a virtual segment into the sorted set
        addInterval(new int[] {-1, N});
    }

    // remove a segment
    private void removeInterval(int[] intv) {
        pq.remove(intv);
        startMap.remove(intv[0]);
        endMap.remove(intv[1]);
    }

    // add a segment
    private void addInterval(int[] intv) {
        pq.add(intv);
        startMap.put(intv[0], intv);
        endMap.put(intv[1], intv);
    }

    // calculate the length of a segment
    private int distance(int[] intv) {
        return intv[1] - intv[0] - 1;
    }

    // ...
}

"Virtual line segment" is essentially a method to represent all seats as one line segment:

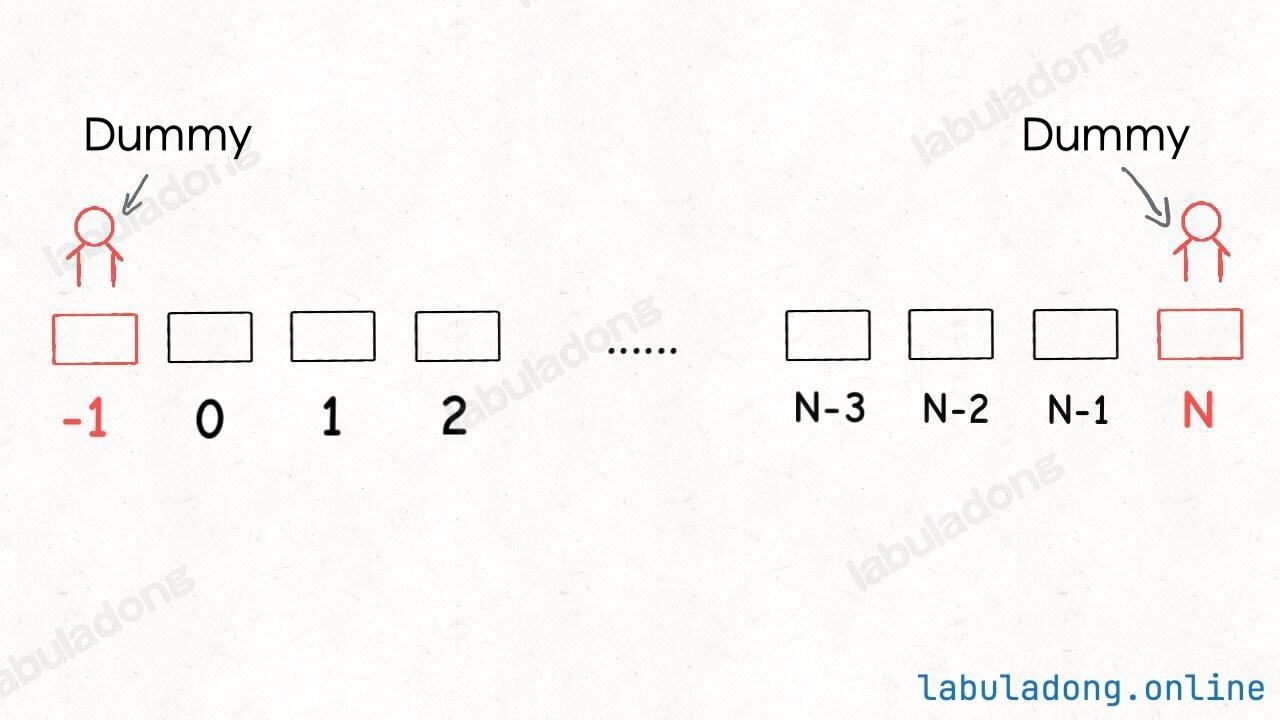
With this setup, the main APIs seat and leave can be implemented:

class ExamRoom {
    // ...

    public int seat() {
        // take the longest segment from the ordered set
        int[] longest = pq.last();
        int x = longest[0];
        int y = longest[1];
        int seat;
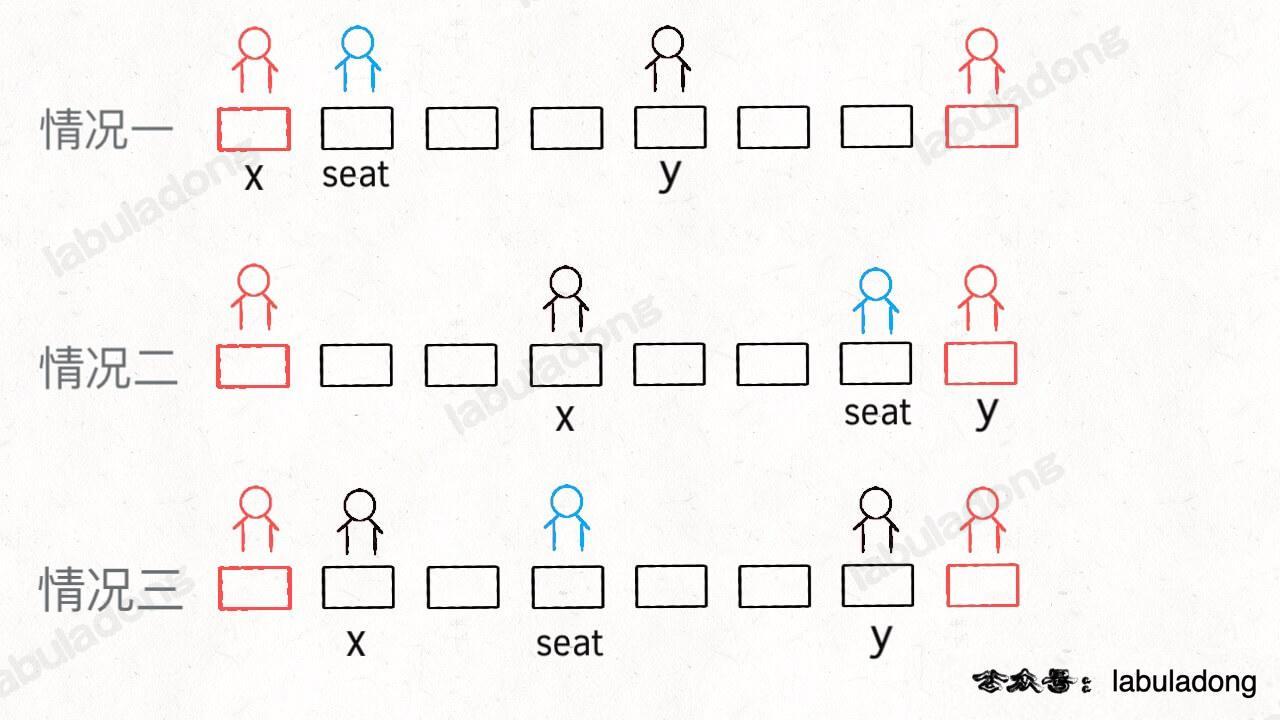
            // case 1
            seat = 0;
            // case 2
            seat = N - 1;
            // case 3
            seat = (y - x) / 2 + x;
        }
        // divide the longest segment into two parts
        int[] left = new int[] {x, seat};
        int[] right = new int[] {seat, y};
        removeInterval(longest);
        addInterval(left);
        addInterval(right);
        return seat;
    }

    public void leave(int p) {
        // find the segments to the left and right of p
        int[] right = startMap.get(p);
        int[] left = endMap.get(p);
        // merge the two segments into one
        int[] merged = new int[] {left[0], right[1]};
        removeInterval(left);
        removeInterval(right);
        addInterval(merged);
    }
}

At this point, the algorithm is basically implemented. Although there is a lot of code, the idea is simple: find the longest segment, split it into two parts, and the midpoint is the return value of seat(). Find the left and right segments of p and merge them into one segment, which is the logic of leave(p).

III. Advanced Issues

However, the problem requires selecting the seat with the smallest index when there are multiple choices. We ignored this issue earlier. For example, the following situation can cause errors:

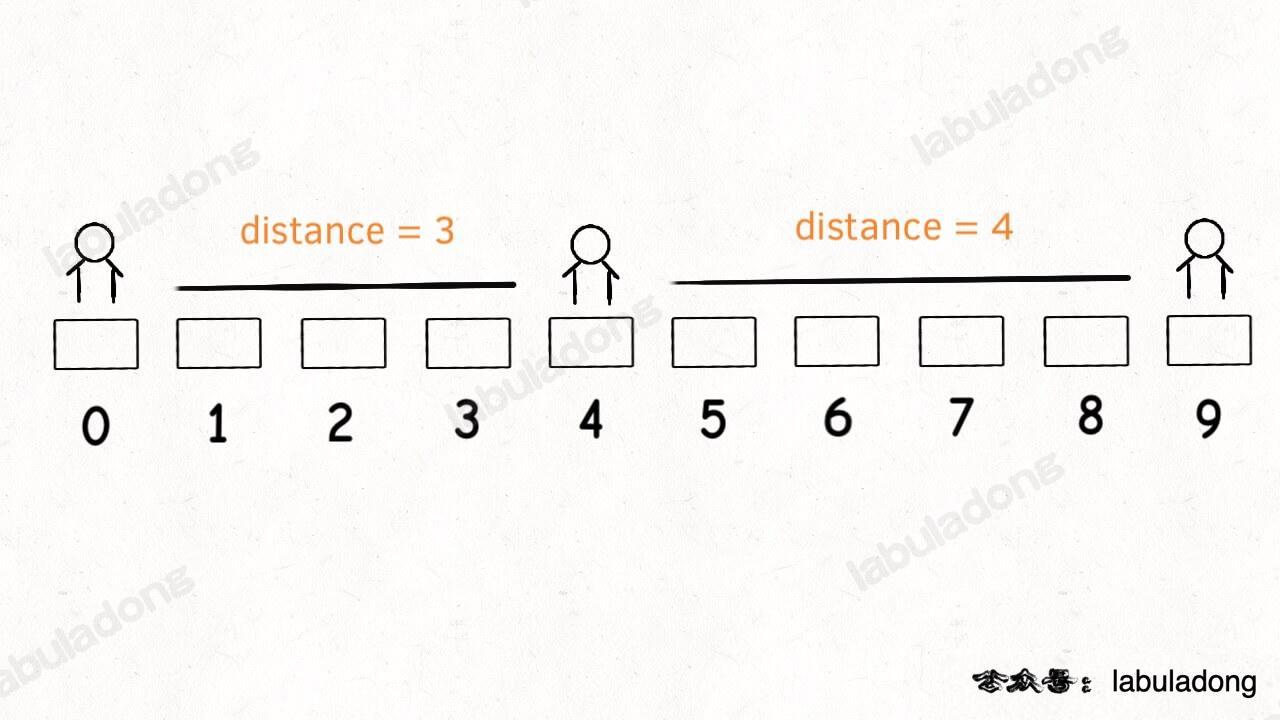
Now, in the ordered set, there are segments [0,4] and [4,9]. The longest segment longest is the latter. According to the logic of seat, it will split [4,9], returning seat 6. However, the correct answer should be seat 2, as both 2 and 6 satisfy the condition of maximizing the distance to adjacent students, and the smaller one should be chosen.

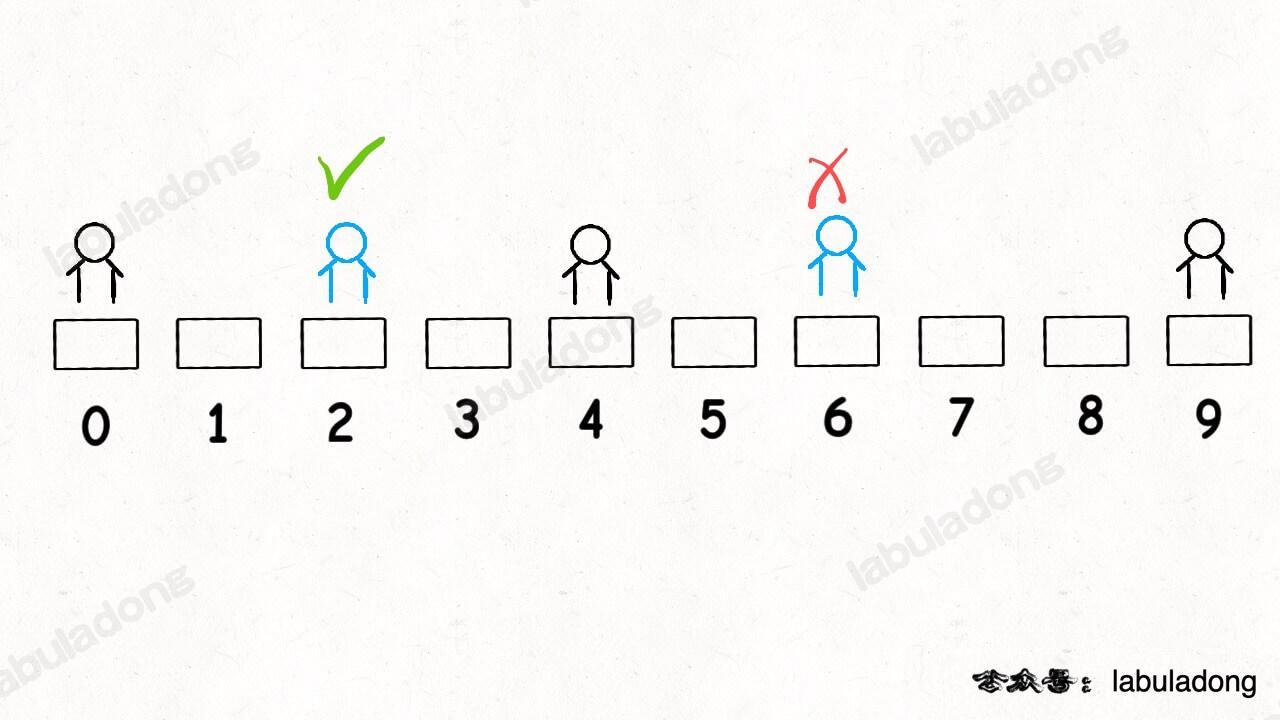
To resolve requirements like this in problems, the solution is to modify the sorting method of the ordered data structure. Specifically for this problem, it involves modifying the comparison function logic of TreeMap.

pq = new TreeSet<>((a, b) -> {
    int distA = distance(a);
    int distB = distance(b);
    // if the distances are the same, compare the indices
    if (distA == distB)
        return b[0] - a[0];
    return distA - distB;
});

In addition, the distance function needs to be modified. It should not simply calculate the length between two endpoints of a line segment, but rather the length between the midpoint and the endpoints of the segment.

class ExamRoom {
    // ...

    private int distance(int[] intv) {
        int x = intv[0];
        int y = intv[1];
        if (x == -1) return y;
        if (y == N) return N - 1 - x;
        // the length between the midpoint and endpoints
        return (y - x) / 2;
    }
}

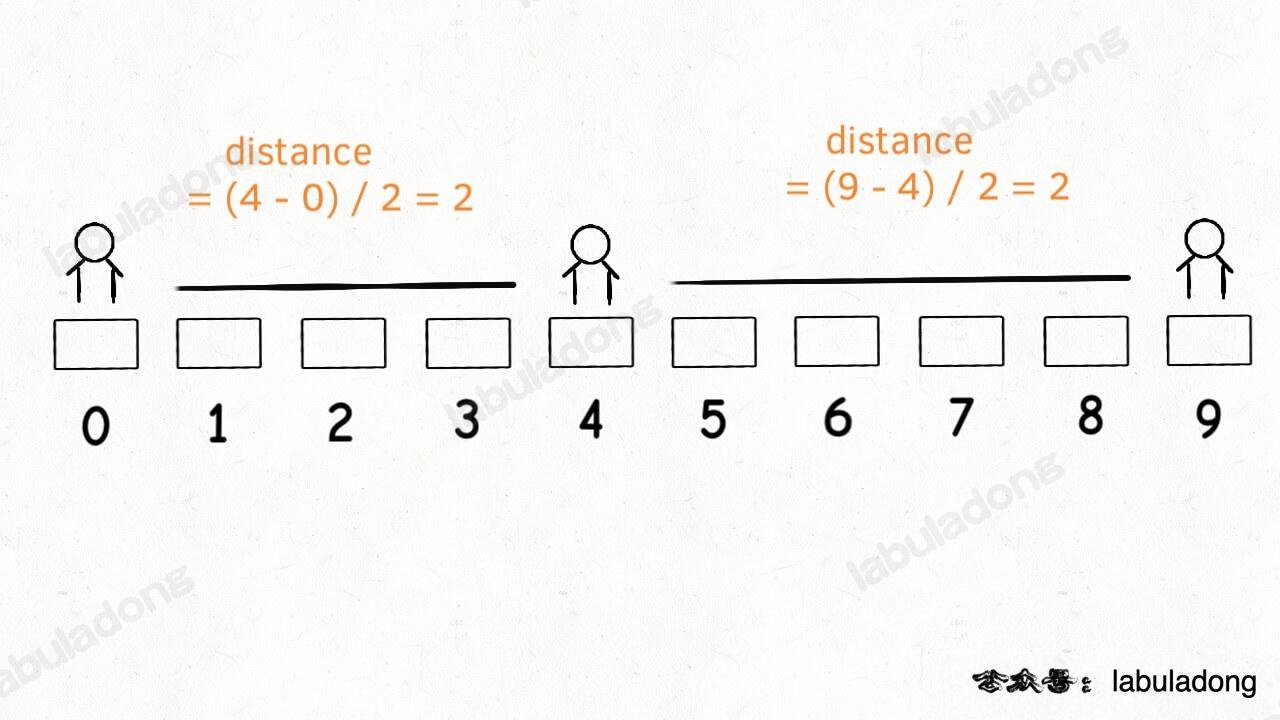
In this way, the distance values of [0,4] and [4,9] become equal. The algorithm will compare their indices and select the smaller segment for division.

This algorithm problem is completely solved. The complete code is as follows:


class ExamRoom {
    // map the endpoint p to the segment with p as the left endpoint
    private Map<Integer, int[]> startMap;
    // map the endpoint p to the segment with p as the right endpoint
    private Map<Integer, int[]> endMap;
    // store all segments in ascending order of their lengths
    private TreeSet<int[]> pq;
    private int N;

    public ExamRoom(int N) {
        this.N = N;
        startMap = new HashMap<>();
        endMap = new HashMap<>();
        pq = new TreeSet<>((a, b) -> {
            int distA = distance(a);
            int distB = distance(b);
            // if the lengths are the same, compare the indices
            if (distA == distB)
                return b[0] - a[0];
            return distA - distB;
        });
        // first put a virtual segment in the ordered set
        addInterval(new int[]{-1, N});
    }

    public int seat() {
        // take out the longest segment from the ordered set
        int[] longest = pq.last();
        int x = longest[0];
        int y = longest[1];
        int seat;
        // case 1
        if (x == -1) {
            seat = 0;
        // case 2
        } else if (y == N) {
            seat = N - 1;
        // case 3
        } else {
            seat = (y - x) / 2 + x;
        }
        // divide the longest segment into two segments
        int[] left = new int[]{x, seat};
        int[] right = new int[]{seat, y};
        removeInterval(longest);
        addInterval(left);
        addInterval(right);
        return seat;
    }

    public void leave(int p) {
        // find the segments to the left and right of p
        int[] right = startMap.get(p);
        int[] left = endMap.get(p);
        // merge the two segments into one segment
        int[] merged = new int[]{left[0], right[1]};
        removeInterval(left);
        removeInterval(right);
        addInterval(merged);
    }

    // add a segment
    private void addInterval(int[] intv) {
        pq.add(intv);
        startMap.put(intv[0], intv);
        endMap.put(intv[1], intv);
    }

    // remove a segment
    private void removeInterval(int[] intv) {
        pq.remove(intv);
        startMap.remove(intv[0]);
        endMap.remove(intv[1]);
    }

    // calculate the length of a segment
    private int distance(int[] intv) {
        int x = intv[0];
        int y = intv[1];
        if (x == -1) return y;
        if (y == N) return N - 1 - x;
        // distance between the midpoint and the endpoint
        return (y - x) / 2;
    }
}