Common Bit Manipulation Techniques
This article will resolve
| LeetCode | Difficulty |
|---|---|
| 136. Single Number | 🟢 |
| 191. Number of 1 Bits | 🟢 |
| 231. Power of Two | 🟢 |
| 268. Missing Number | 🟢 |
Bit manipulation has many tricks. There is a website called “Bit Twiddling Hacks” that collects almost all bit tricks:
http://graphics.stanford.edu/~seander/bithacks.html
But most of these tricks are too hard to read. I think you can use that site like a dictionary, no need to study every line. What we really need to learn are the bit tricks that are interesting and useful.
So in this article, we will start from the basics, explain some simple ideas of bit operations, then summarize some common bit tricks used in algorithm problems and real-world development.
Basics of Bit Operations
Binary representation
In a computer, all data is finally stored in binary form. Binary has only two digits: 0 and 1. Each digit is called a bit.
For example, the decimal number 13 is 1101 in binary:
1101 = 1×2³ + 1×2² + 0×2¹ + 1×2⁰ = 8 + 4 + 0 + 1 = 13In Java and some other languages, we can use the 0b prefix to write binary numbers:
int a = 0b1101; // same as decimal 13
int b = 0b1010; // same as decimal 10Shift operations
Left shift <<: move the bits to the left, and fill 0s on the right. Shifting left by n bits is the same as multiplying by 2^n.
int a = 5; // binary: 0b0101
int b = a << 1; // binary: 0b1010, decimal: 10
int c = a << 2; // binary: 0b10100, decimal: 20
// Left shift n bits is like multiply by 2^n
// 5 << 1 = 5 * 2¹ = 10
// 5 << 2 = 5 * 2² = 20Right shift >>: move the bits to the right, and fill the left side with the sign bit. Shifting right by n bits is like dividing by 2^n and taking the floor.
int a = 20; // binary: 0b10100
int b = a >> 1; // binary: 0b1010, decimal: 10
int c = a >> 2; // binary: 0b101, decimal: 5
// Right shift n bits is like divide by 2^n
// 20 >> 1 = 20 / 2¹ = 10
// 20 >> 2 = 20 / 2² = 5AND operation
AND &: the result bit is 1 only when both bits are 1, otherwise it is 0.
int a = 12; // binary: 0b1100
int b = 10; // binary: 0b1010
int c = a & b; // binary: 0b1000, decimal: 8
// bit by bit:
// 1100
// 1010
// ----
// 1000Common uses:
- Check odd or even:
n & 1, result 1 means odd, 0 means even - Get a specific bit:
n & (1 << k)can get the k-th bit of n
int n = 13; // binary: 0b1101
boolean isOdd = (n & 1) == 1; // true, 13 is odd
// get bit 2 (count from right, starting at 0)
int bit2 = (n & (1 << 2)) != 0 ? 1 : 0; // result is 1OR operation
OR |: the result bit is 1 if at least one of the bits is 1.
int a = 12; // binary: 0b1100
int b = 10; // binary: 0b1010
int c = a | b; // binary: 0b1110, decimal: 14
// bit by bit:
// 1100
// 1010
// ----
// 1110Common uses:
- Set a specific bit to 1:
n | (1 << k)sets the k-th bit of n to 1
int n = 12; // binary: 0b1100
n = n | (1 << 0); // set bit 0 to 1, result: 0b1101, decimal: 13XOR operation
XOR ^: the result bit is 1 only when the two bits are different; if they are the same, the result is 0.
int a = 12; // binary: 0b1100
int b = 10; // binary: 0b1010
int c = a ^ b; // binary: 0b0110, decimal: 6
// bit by bit:
// 1100
// 1010
// ----
// 0110Important properties of XOR:
a ^ a = 0: any number XOR itself is 0a ^ 0 = a: any number XOR 0 is itself- XOR is commutative and associative:
a ^ b ^ c = a ^ (b ^ c) = (a ^ b) ^ c
int a = 5;
int result1 = a ^ a; // result is 0
int result2 = a ^ 0; // result is 5
// commutative and associative
int x = 3, y = 5, z = 7;
int r1 = x ^ y ^ z; // result is 1
int r2 = x ^ (y ^ z); // result is 1
int r3 = (x ^ y) ^ z; // result is 1Common uses:
- Flip a specific bit:
n ^ (1 << k)flips the k-th bit of n (0 -> 1, 1 -> 0) - Swap two numbers (will be explained later)
int n = 12; // binary: 0b1100
n = n ^ (1 << 0); // flip bit 0, result: 0b1101, decimal: 13
n = n ^ (1 << 0); // flip bit 0 again, result: 0b1100, decimal: 12Once we understand these basic bit operations, we can move on to some interesting bit tricks.
Some Interesting Bit Operations
// 1. Use OR `|` with space to convert English letters to lowercase
('a' | ' ') = 'a'
('A' | ' ') = 'a'
// 2. Use AND `&` with underscore to convert English letters to uppercase
('b' & '_') = 'B'
('B' & '_') = 'B'
// 3. Use XOR `^` with space to flip letter case
('d' ^ ' ') = 'D'
('D' ^ ' ') = 'd'
// These work because of ASCII codes.
// Characters are actually numbers, and the codes for space and underscore
// can flip case through bit operations.
// If you are interested, you can check the ASCII table and do the math yourself.
// 4. Swap two numbers without a temp variable
int a = 1, b = 2;
a ^= b;
b ^= a;
a ^= b;
// now a = 2, b = 1
// 5. Add one
int n = 1;
n = -~n;
// now n = 2
// 6. Subtract one
int n = 2;
n = ~-n;
// now n = 1
// 7. Check if two numbers have different signs
int x = -1, y = 2;
boolean f = ((x ^ y) < 0); // true
int x = 3, y = 2;
boolean f = ((x ^ y) < 0); // falseThe first 6 tricks are not very useful in real code. But the 7th trick is quite practical. It uses the sign bit in two’s complement.
In integer encoding, the highest bit is the sign bit. For negative numbers, the sign bit is 1. For non-negative numbers, the sign bit is 0. With XOR, you can know whether two numbers have different signs.
If you do not use bit operations, you must use if-else to check the sign, which is more trouble. You may think of using the product to check the sign, but that can easily cause integer overflow and give wrong results.
Modulo with Power of 2
For modulus (remainder), we usually use the % operator. But in some code (for example, in the source code of HashMap), you may see & instead. This is an optimization.
When the modulus m is a power of 2, x % m is the same as x & (m - 1).
The bit operation & is much faster than %, so this trick is very useful where performance matters.
A common use is in a circular array. The normal way is to use % so that the index loops in [0, arr.length - 1]:
int[] arr = {1,2,3,4};
int index = 0;
while (true) {
// looping in a circular array
print(arr[index % arr.length]);
index++;
}
// output: 1,2,3,4,1,2,3,4,1,2,3,4...int arr[] = {1, 2, 3, 4};
int index = 0;
while (true) {
// loop through the circular array
cout << arr[index % (sizeof(arr) / sizeof(int))] << endl;
index++;
}
// output: 1,2,3,4,1,2,3,4,1,2,3,4...arr = [1,2,3,4]
index = 0
while True:
# Loop through the circular array
print(arr[index % len(arr)])
index += 1
# Output: 1,2,3,4,1,2,3,4,1,2,3,4...arr := []int{1, 2, 3, 4}
index := 0
for {
// Looping in a circular array
fmt.Print(arr[index%len(arr)])
index++
}
// Output: 1,2,3,4,1,2,3,4,1,2,3,4...var arr = [1, 2, 3, 4];
var index = 0;
while (true) {
// looping in a circular array
console.log(arr[index % arr.length]);
index++;
}
// output: 1,2,3,4,1,2,3,4,1,2,3,4...If the array length is a power of 2, we can use & to speed up the modulus:
int[] arr = {1,2,3,4};
int index = 0;
while (true) {
// loop in the circular array
print(arr[index & (arr.length - 1)]);
index++;
}
// output: 1,2,3,4,1,2,3,4,1,2,3,4...vector<int> arr = {1, 2, 3, 4};
int index = 0;
while (true) {
// Looping in a circular array
cout << arr[index & (arr.size() - 1)] << " ";
index++;
}
// Output: 1,2,3,4,1,2,3,4,1,2,3,4...arr = [1, 2, 3, 4]
index = 0
while True:
# Loop in a circular array
print(arr[index & (len(arr) - 1)], end=", ")
index += 1
# Output: 1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4, ...arr := []int{1, 2, 3, 4}
index := 0
for {
// loop in a circular array
fmt.Print(arr[index&(len(arr)-1)])
index++
}
// output: 1,2,3,4,1,2,3,4,1,2,3,4...var arr = [1,2,3,4];
var index = 0;
while (true) {
// loop through the circular array
console.log(arr[index & (arr.length - 1)]);
index++;
}
// output: 1,2,3,4,1,2,3,4,1,2,3,4...Important
This trick only works when the array length is a power of 2, like 2, 4, 8, 16, 32, and so on. There are clever bit hacks that can round a number up to a power of 2. You can check https://graphics.stanford.edu/~seander/bithacks.html#RoundUpPowerOf2
Simply put, & (arr.length - 1) can replace % arr.length and gives better performance.
Now another question: we keep doing index++, and this gives us a circular effect. But if we keep doing index--, can we still get a circular array?
If you use % for modulus, once index becomes negative, the result of % can also be negative, and you must handle this case specially. But with &, index will not become negative and everything still works:
int[] arr = {1,2,3,4};
int index = 0;
while (true) {
// looping in a circular array
print(arr[index & (arr.length - 1)]);
index--;
}
// output: 1,4,3,2,1,4,3,2,1,4,3,2,1...int arr[] = {1,2,3,4};
int index = 0;
while (true) {
// Loop in a circular array
cout << arr[index & (sizeof(arr) / sizeof(*arr) - 1)] << " ";
index--;
}
// Output: 1,4,3,2,1,4,3,2,1,4,3,2,1...arr = [1, 2, 3, 4]
index = 0
while True:
# Looping in a circular array
print(arr[index & (len(arr) - 1)])
index -= 1arr := []int{1, 2, 3, 4}
index := 0
for {
// looping in a circular array
fmt.Print(arr[index&(len(arr)-1)])
index--
}
// output: 1,4,3,2,1,4,3,2,1,4,3,2,1...var arr = [1,2,3,4];
var index = 0;
while (true) {
console.log(arr[index & (arr.length - 1)]);
index--;
}
// Output: 1,4,3,2,1,4,3,2,1,4,3,2,1...You may not use this trick often in your own code, but you will see it a lot when reading other code bases. Just keep it in mind so you are not confused when you see it.
The Usage of n & (n-1)
The operation n & (n-1) is common in algorithms, and its effect is to remove the last 1 in the binary form of n.
Look at the picture and it becomes clear:
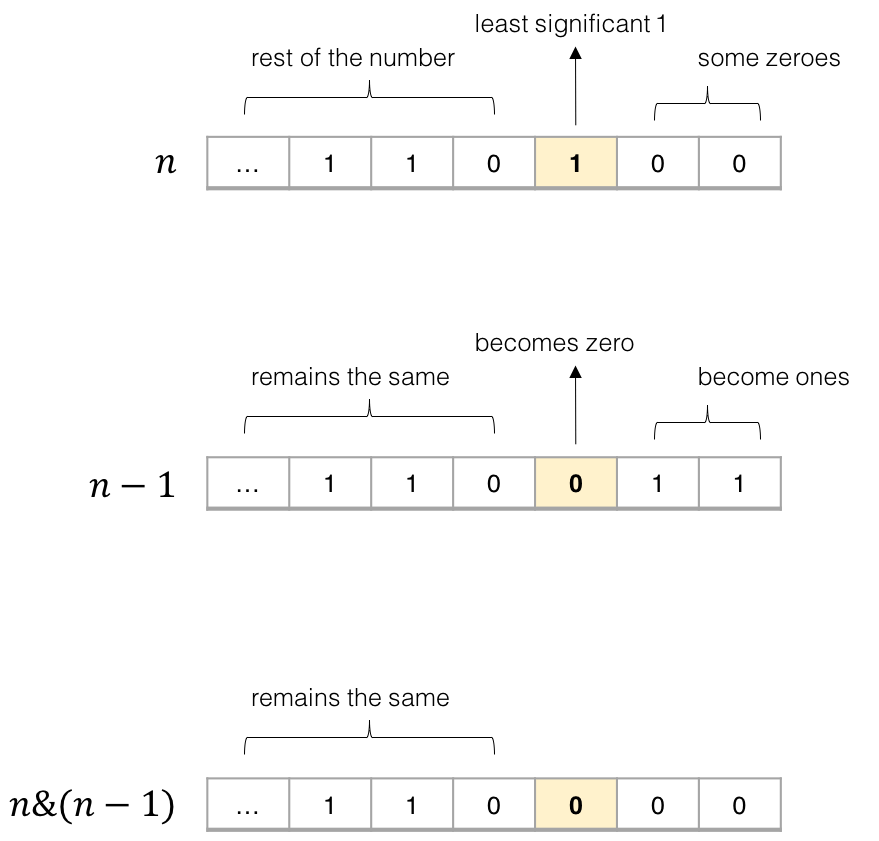
The key idea: n - 1 will remove the last 1 in n, and turn all the bits after it into 1. Then n & (n - 1) will clear only that last 1 to 0.
Hamming Weight
This is LeetCode 191: “Number of 1 Bits”:
191. Number of 1 Bits | LeetCode | 🟢
Write a function that takes the binary representation of a positive integer and returns the number of set bits it has (also known as the Hamming weight).
Example 1:
Input: n = 11
Output: 3
Explanation:
The input binary string 1011 has a total of three set bits.
Example 2:
Input: n = 128
Output: 1
Explanation:
The input binary string 10000000 has a total of one set bit.
Example 3:
Input: n = 2147483645
Output: 30
Explanation:
The input binary string 1111111111111111111111111111101 has a total of thirty set bits.
Constraints:
1 <= n <= 231 - 1
You need to return how many 1s are in the binary form of n. Since n & (n - 1) can remove the last 1, we can keep doing this in a loop and count, until n becomes 0.
public class Solution {
// you need to treat n as an unsigned value
public int hammingWeight(int n) {
int res = 0;
while (n != 0) {
n = n & (n - 1);
res++;
}
return res;
}
}#include <vector>
#include <string>
class Solution {
public:
int hammingWeight(uint32_t n) {
int res = 0;
while (n != 0) {
n = n & (n - 1);
res++;
}
return res;
}
};class Solution:
def hammingWeight(self, n: int) -> int:
res = 0
while n != 0:
n = n & (n - 1)
res += 1
return resfunc hammingWeight(n int) int {
res := 0
for n != 0 {
n = n & (n - 1)
res++
}
return res
}var hammingWeight = function(n) {
let res = 0;
while (n != 0) {
n = n & (n - 1);
res++;
}
return res;
};Check If a Number Is a Power of 2
This is LeetCode 231: “Power of Two”.
If a number is a power of 2, its binary form has exactly one 1:
2^0 = 1 = 0b0001
2^1 = 2 = 0b0010
2^2 = 4 = 0b0100Using the trick n & (n - 1) makes it easy (note operator precedence, you cannot remove the parentheses):
class Solution {
public boolean isPowerOfTwo(int n) {
if (n <= 0) return false;
return (n & (n - 1)) == 0;
}
}class Solution {
public:
bool isPowerOfTwo(int n) {
if (n <= 0) return false;
return (n & (n - 1)) == 0;
}
};class Solution:
def isPowerOfTwo(self, n: int) -> bool:
if n <= 0:
return False
return (n & (n - 1)) == 0func isPowerOfTwo(n int) bool {
if n <= 0 {
return false
}
return (n & (n - 1)) == 0
}var isPowerOfTwo = function(n) {
if (n <= 0) return false;
return (n & (n - 1)) === 0;
};The Usage of a ^ a = 0
We must remember these properties of XOR:
A number XOR itself is 0, that is a ^ a = 0.
A number XOR 0 is the number itself, that is a ^ 0 = a.
Find the Element That Appears Only Once
This is LeetCode 136: “Single Number”:
136. Single Number | LeetCode | 🟢
Given a non-empty array of integers nums, every element appears twice except for one. Find that single one.
You must implement a solution with a linear runtime complexity and use only constant extra space.
Example 1:
Input: nums = [2,2,1] Output: 1
Example 2:
Input: nums = [4,1,2,1,2] Output: 4
Example 3:
Input: nums = [1] Output: 1
Constraints:
1 <= nums.length <= 3 * 104-3 * 104 <= nums[i] <= 3 * 104- Each element in the array appears twice except for one element which appears only once.
For this problem, we just XOR all numbers together. Pairs of equal numbers will become 0. The single number XOR 0 is still itself, so the final XOR result is the element that appears only once:
class Solution {
public int singleNumber(int[] nums) {
int res = 0;
for (int n : nums) {
res ^= n;
}
return res;
}
}#include <vector>
class Solution {
public:
int singleNumber(std::vector<int>& nums) {
int res = 0;
for (int n : nums) {
res ^= n;
}
return res;
}
};class Solution:
def singleNumber(self, nums: List[int]) -> int:
res = 0
for n in nums:
res ^= n
return resfunc singleNumber(nums []int) int {
res := 0
for _, n := range nums {
res ^= n
}
return res
}var singleNumber = function(nums) {
let res = 0;
for (let n of nums) {
res ^= n;
}
return res;
};Find the Missing Number
This is LeetCode Problem 268: Missing Number:
268. Missing Number | LeetCode | 🟢
Given an array nums containing n distinct numbers in the range [0, n], return the only number in the range that is missing from the array.
Example 1:
Input: nums = [3,0,1] Output: 2 Explanation: n = 3 since there are 3 numbers, so all numbers are in the range [0,3]. 2 is the missing number in the range since it does not appear in nums.
Example 2:
Input: nums = [0,1] Output: 2 Explanation: n = 2 since there are 2 numbers, so all numbers are in the range [0,2]. 2 is the missing number in the range since it does not appear in nums.
Example 3:
Input: nums = [9,6,4,2,3,5,7,0,1] Output: 8 Explanation: n = 9 since there are 9 numbers, so all numbers are in the range [0,9]. 8 is the missing number in the range since it does not appear in nums.
Constraints:
n == nums.length1 <= n <= 1040 <= nums[i] <= n- All the numbers of
numsare unique.
Follow up: Could you implement a solution using only O(1) extra space complexity and O(n) runtime complexity?
You are given an array of length n. The valid indices are [0, n), but now you want to put n + 1 numbers [0, n] into it. So one number must be missing. Please find this missing number.
This problem is not hard. We can easily think of sorting the array first, then scan it once to find the missing number.
Or we can use a data structure: put all numbers from the array into a HashSet, then iterate through the numbers in [0, n] and check which one is not in the HashSet.
The sorting solution has time complexity O(NlogN). The HashSet solution has time complexity O(N), but it also needs O(N) extra space to store the HashSet.
There is a very simple solution for this problem: the sum formula of an arithmetic sequence.
We can understand the problem like this: we have an arithmetic sequence 0, 1, 2, ..., n, and one number is missing. We need to find it. Then the answer is:
sum(0, 1, ..., n) - sum(nums).
int missingNumber(int[] nums) {
int n = nums.length;
// Although the data range given by the problem is not large, we should
// use long type to prevent integer overflow for the sake of rigor
// Sum formula: (first term + last term) * number of terms / 2
long expect = (0 + n) * (n + 1) / 2;
long sum = 0;
for (int x : nums) {
sum += x;
}
return (int)(expect - sum);
}int missingNumber(vector<int>& nums) {
int n = nums.size();
// Although the data range given by the problem is not large, we should
// use long type to prevent integer overflow for the sake of rigor
// Sum formula: (first term + last term) * number of terms / 2
long expect = (0 + n) * (n + 1) / 2;
long sum = 0;
for (int x : nums) {
sum += x;
}
return (int)(expect - sum);
}from typing import List
def missingNumber(nums: List[int]) -> int:
n = len(nums)
# Although the data range given by the problem is not large,
# it's rigorous to use long type to prevent integer overflow
# Sum formula: (first term + last term) * number of terms / 2
expect = (0 + n) * (n + 1) / 2
sum_ = 0
for x in nums:
sum_ += x
return int(expect - sum_)func missingNumber(nums []int) int {
n := len(nums)
// Although the data range given by the problem is not large, to
// be rigorous, use long type to prevent integer overflow
// Sum formula: (first term + last term) * number of terms / 2
expect := (0 + n) * (n + 1) / 2
var sum int64
for _, x := range nums {
sum += int64(x)
}
return int(expect - sum)
}var missingNumber = function(nums) {
var n = nums.length;
// Although the data range given by the problem is not large, we should
// use long type to prevent integer overflow for the sake of rigor
// Sum formula: (first term + last term) * number of terms / 2
var expect = (0 + n) * (n + 1) / 2;
var sum = 0;
for (var i = 0; i < n; i++) {
sum += nums[i];
}
return (expect - sum);
};But the main topic of this article is bit operations. So we will see how to use bit tricks to solve this problem.
Recall the properties of XOR:
- A number XOR itself is 0.
- A number XOR 0 is still the number itself.
XOR also has commutative and associative laws. That is:
2 ^ 3 ^ 2 = 3 ^ (2 ^ 2) = 3 ^ 0 = 3We can use these properties to find the missing number. For example, nums = [0, 3, 1, 4]:
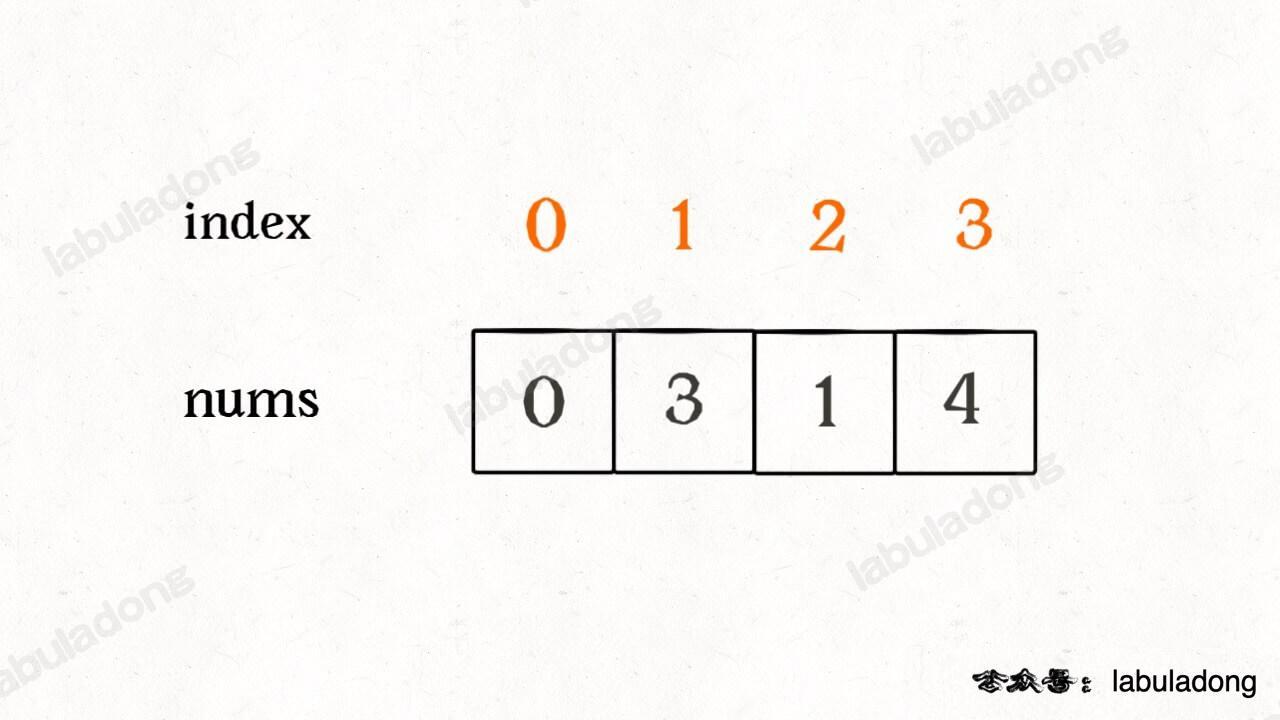
To make it easier to understand, we first imagine extending the index by one, then match each element with the index that has the same value:
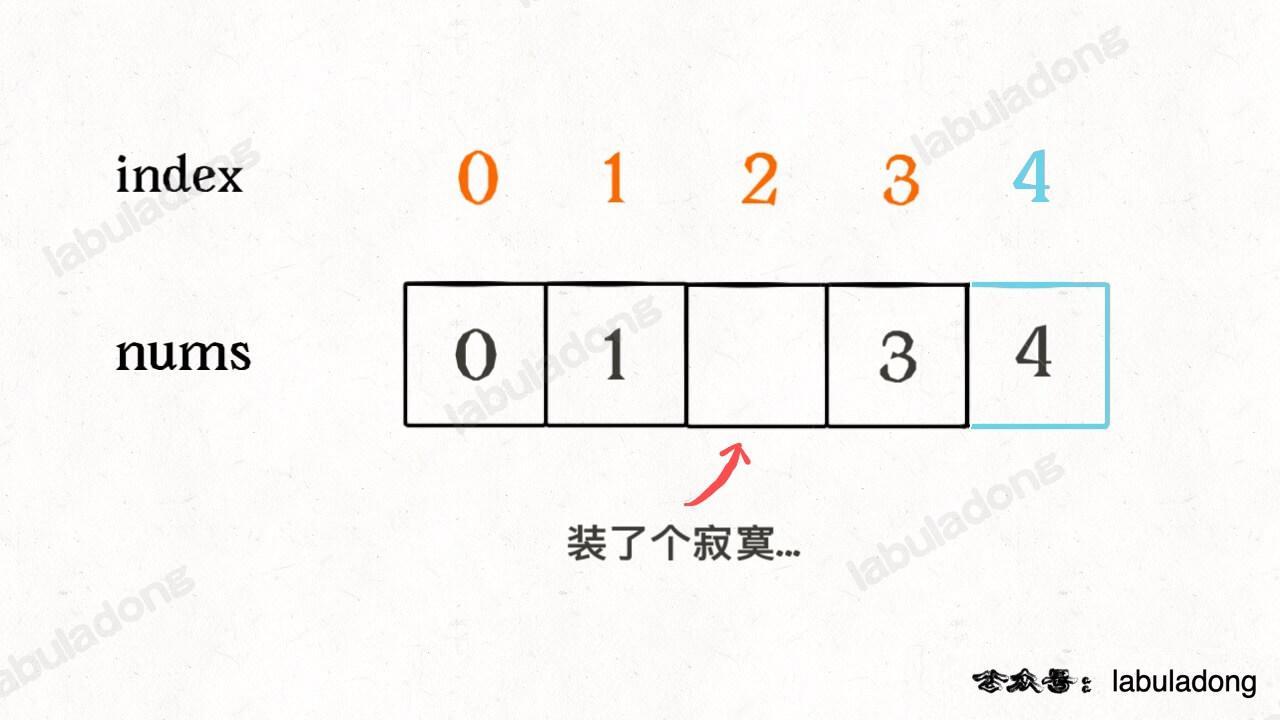
After doing this, except for the missing number, every index and element form a pair. If we can find the lonely index 2, we find the missing number.
How do we find this lonely number? Just XOR all the indices and all the elements together. All paired numbers will cancel out to 0, and only the lonely one will remain. That is our answer:
class Solution {
public int missingNumber(int[] nums) {
int n = nums.length;
int res = 0;
// first XOR with the new added index
res ^= n;
// XOR with other elements and indices
for (int i = 0; i < n; i++)
res ^= i ^ nums[i];
return res;
}
}#include <vector>
using namespace std;
class Solution {
public:
int missingNumber(vector<int>& nums) {
int n = nums.size();
int res = 0;
// first XOR with the new added index
res ^= n;
// XOR with other elements and indices
for (int i = 0; i < n; i++)
res ^= i ^ nums[i];
return res;
}
};class Solution:
def missingNumber(self, nums: List[int]) -> int:
n = len(nums)
res = 0
# first XOR with the new added index
res ^= n
# XOR with other elements and indices
for i in range(n):
res ^= i ^ nums[i]
return resfunc missingNumber(nums []int) int {
n := len(nums)
res := 0
// first XOR with the new added index
res ^= n
// XOR with other elements and indices
for i := 0; i < n; i++ {
res ^= i ^ nums[i]
}
return res
}var missingNumber = function(nums) {
let n = nums.length;
let res = 0;
// first XOR with the new added index
res ^= n;
// XOR with other elements and indices
for (let i = 0; i < n; i++)
res ^= i ^ nums[i];
return res;
};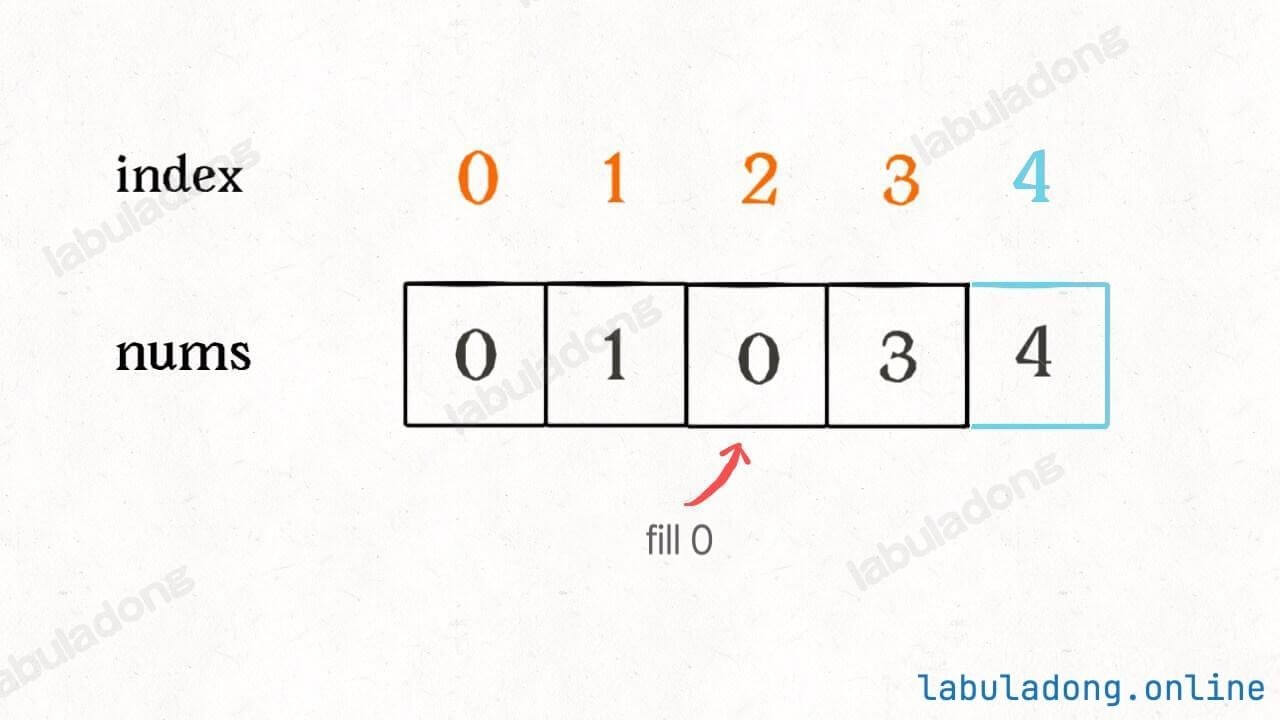
Because XOR is commutative and associative, we can always cancel all pairs and keep only the missing number.
Up to here, we have covered most common bit operations. These tricks are easy once you get them, and you do not need to memorize them. Just keep a rough idea in mind, and that is enough.