Binary Search in Action
This article will resolve
| LeetCode | Difficulty |
|---|---|
| 1011. Capacity To Ship Packages Within D Days | 🟠 |
| 410. Split Array Largest Sum | 🔴 |
| 875. Koko Eating Bananas | 🟠 |
In Detailed Binary Search Framework, we studied the details of binary search: searching for a single element, searching for the left boundary, and searching for the right boundary. That article teaches you how to write correct binary search code without bugs.
However, that framework is only for the basic case: searching for a number in a sorted array. In real problems, things are less direct, and sometimes it’s hard to see if binary search can be used.
So, this article will give you a set of ideas for applying binary search. When you see a problem related to binary search, you will know how to think about it step by step and write the correct answer.
Original Binary Search Code
The classic binary search is used to find a target element in a sorted array and return its index.
If the target does not exist, you can return a special value. This is just a detail that can be adjusted in the code.
Another important point: if the sorted array has more than one target element, those elements are together. Should the code return the index of the first one or the last one? This is called "searching for the left boundary" and "searching for the right boundary", and you can control it by slightly changing the code.
In Detailed Binary Search Framework, we talked deeply about these problems. If you are not clear about them, you should review the article. If you already know the basic binary search, you can continue here.
In real algorithm problems, you usually need to search for the left boundary or the right boundary, not just a single element.
Most algorithm problems ask you to find the maximum or minimum values, such as the "minimum speed to eat bananas" or the "minimum capacity of a ship". These are all about searching for boundaries, so we will focus on these two types of binary search code.
Note
All code in this article uses the "left-closed, right-open" binary search style. If you like the "closed on both ends" style, you can change the code yourself.
Here is the code for "searching for the left boundary" using binary search:
// search for the left boundary
int left_bound(int[] nums, int target) {
if (nums.length == 0) return -1;
int left = 0, right = nums.length;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
// when target is found, shrink the right boundary
right = mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
return left;
}// search for the left boundary
int left_bound(vector<int>& nums, int target) {
if (nums.size() == 0) return -1;
int left = 0, right = nums.size();
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
// when target is found, shrink the right boundary
right = mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
return left;
}def left_bound(nums: List[int], target: int) -> int:
# search for the left boundary
if len(nums) == 0:
return -1
left, right = 0, len(nums)
while left < right:
mid = left + (right - left) // 2
if nums[mid] == target:
# when target is found, shrink the right boundary
right = mid
elif nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
right = mid
return left// Search for the left boundary
func left_bound(nums []int, target int) int {
if len(nums) == 0 {
return -1
}
left, right := 0, len(nums)
for left < right {
mid := left + (right - left) / 2
if nums[mid] == target {
// When target is found, shrink the right boundary
right = mid
} else if nums[mid] < target {
left = mid + 1
} else if nums[mid] > target {
right = mid
}
}
return left
}// search for the left boundary
var left_bound = function(nums, target) {
if (nums.length === 0) return -1;
let left = 0, right = nums.length;
while (left < right) {
let mid = left + Math.floor((right - left) / 2);
if (nums[mid] === target) {
// when target is found, shrink the right boundary
right = mid;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
return left;
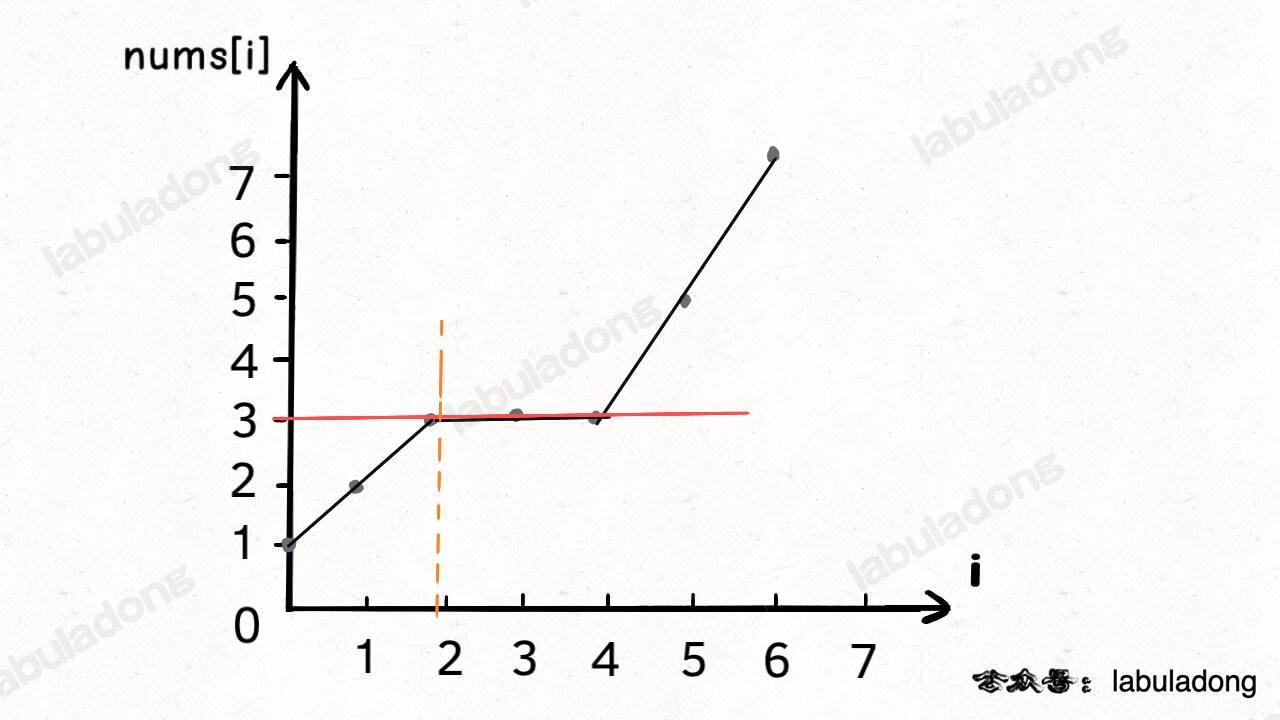
};If the input array is nums = [1,2,3,3,3,5,7] and the target is 3, the algorithm will return index 2.
The image below shows what this looks like:
The code for "searching for the right boundary" with binary search is below:
// search for the right boundary
int right_bound(int[] nums, int target) {
if (nums.length == 0) return -1;
int left = 0, right = nums.length;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
// when target is found, shrink the left boundary
left = mid + 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
return left - 1;
}// search for the right boundary
int right_bound(vector<int>& nums, int target) {
if (nums.size() == 0) return -1;
int left = 0, right = nums.size();
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) {
// when target is found, shrink the left boundary
left = mid + 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
return left - 1;
}# Search for the right boundary
def right_bound(nums: list[int], target: int) -> int:
if len(nums) == 0:
return -1
left, right = 0, len(nums)
while left < right:
mid = left + (right - left) // 2
if nums[mid] == target:
# When target is found, shrink the left boundary
left = mid + 1
elif nums[mid] < target:
left = mid + 1
elif nums[mid] > target:
right = mid
return left - 1// Search for the right boundary
func right_bound(nums []int, target int) int {
if len(nums) == 0 {
return -1
}
left, right := 0, len(nums)
for left < right {
mid := left + (right-left)/2
if nums[mid] == target {
// When target is found, shrink the left boundary
left = mid + 1
} else if nums[mid] < target {
left = mid + 1
} else if nums[mid] > target {
right = mid
}
}
return left - 1
}// search for the right boundary
var right_bound = function(nums, target) {
if (nums.length === 0) return -1;
let left = 0, right = nums.length;
while (left < right) {
let mid = left + Math.floor((right - left) / 2);
if (nums[mid] === target) {
// when target is found, shrink the left boundary
left = mid + 1;
} else if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid;
}
}
return left - 1;
};With the same input, the algorithm will return index 4. The picture looks like this:
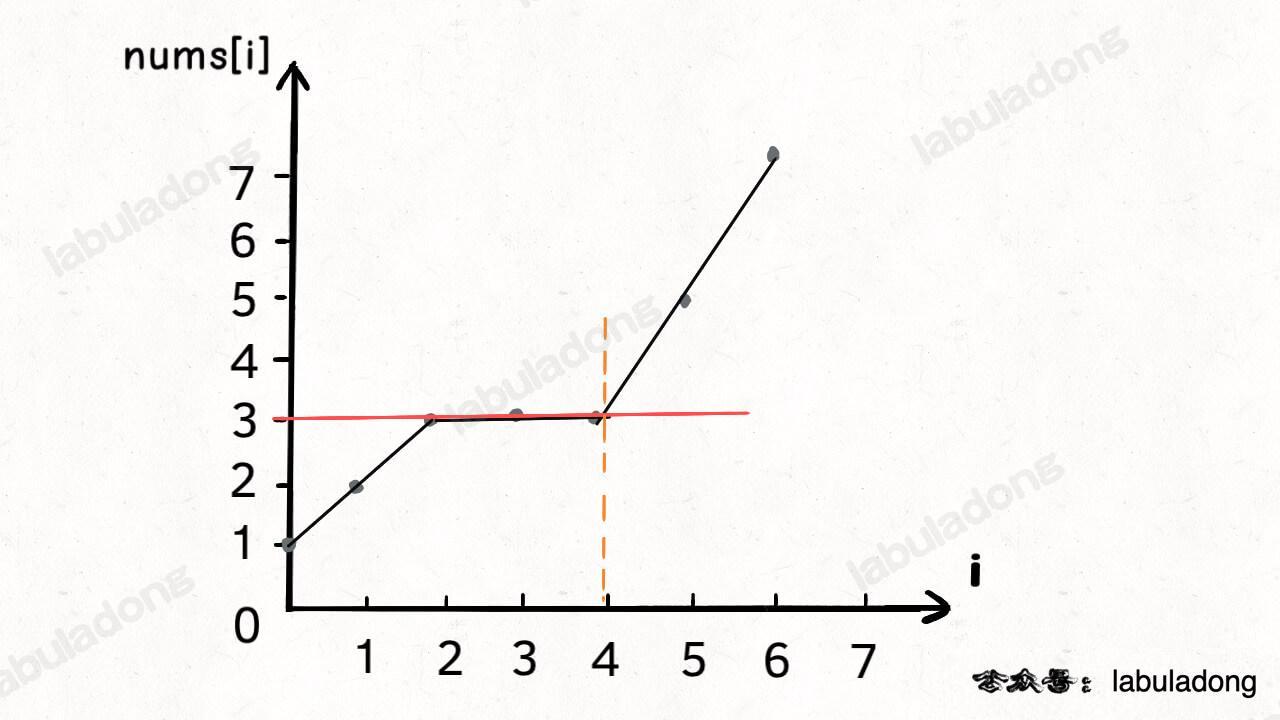
These are review points. If you have read this far, you should understand them. Remember these images. Any problem that can look like these images can be solved with binary search.