One Perspective + Two Thinking Patterns to Master Recursion

This article clarifies:

1. The essence of algorithms is brute-force, and recursion is an important means of brute-force. The correct way to understand recursion is from the perspective of a "tree."

2. There are two thinking modes for writing recursive algorithms: one is to obtain the answer by "traversing" the tree, and the other is to obtain the answer by "decomposing the problem."

The main purpose of this article is to clarify the correct thinking method with the help of the visualization panel, without delving into code details. There are dedicated sections on this site explaining various recursive algorithms and exercises, all following the thinking mode explained in the text. With the foundation laid by this article, learning will be more effective.

Understanding Recursion from the Perspective of a Tree

For beginners, recursive algorithms are indeed not easy to understand, and I was no exception when I first learned algorithms.

I once imagined some interesting perspectives to understand recursion, such as placing two mirrors opposite each other, where the images in the mirrors would infinitely nest, which seems to be a manifestation of recursion?

Moreover, from the principle of program operation, the call of a recursive function is essentially a process of pushing and popping the stack, so it should be understandable from the perspective of a stack?

As my understanding of algorithms deepened, I can now responsibly tell you that the most effective way to understand and write recursive algorithms is from the perspective of a "tree," and all else is merely superficial and impractical.

I will use two simple classic algorithm problems, the Fibonacci tree and permutations, to demonstrate this point.

Again, the focus of this article is on the thinking method rather than the code, so there is no need to dwell on code details. Please use the visualization panel and focus on understanding the abstraction of the "recursion tree" and the difference between the "traversal" and "problem decomposition" thinking modes.

Fibonacci Sequence

Let's first look at a simple yet classic problem: the Fibonacci sequence.

The mathematical definition of the Fibonacci sequence is as follows:

$$fib(n) = \begin{cases} 0 & n = 0 \\ 1 & n = 1 \\ fib(n-1) + fib(n-2) & n > 1 \end{cases}$$

比方说：

$$\begin{aligned} & fib(4) \\ & = fib(3) + fib(2) \\ & = (fib(2) + fib(1)) + (fib(1) + fib(0)) \\ & = ((fib(1) + fib(0)) + fib(1)) + (fib(1) + fib(0)) \\ & = ((1 + 0) + 1) + (1 + 0) = 3 \end{aligned}$$

Now, please write a function that takes an integer $n$ as input and returns the value of the Fibonacci sequence $fib(n)$:

int fib(int n);

By directly translating the mathematical definition of the Fibonacci sequence into code, we can obtain a recursive solution:

int fib(int n) {
    if (n < 2) {
        return n;
    }
    return fib(n - 1) + fib(n - 2);
}

Certainly, this solution is not very efficient. We will continue to optimize it in Dynamic Programming Core Framework. For now, let's just look at this recursive solution.

Put this solution into the visualization panel, and let's calculate fib(5). Please follow my steps:

Next, I will describe the calculation process of this algorithm:

Firstly, we want to calculate fib(5). According to the algorithm, we need to calculate fib(4) and fib(3), and then sum them.

Let's first calculate the value of fib(4): according to the definition, fib(4) requires calculating fib(3) and fib(2), and then summing them.

Let's first calculate the value of fib(3): according to the definition, fib(3) requires calculating fib(2) and fib(1), and then summing them.

Let's first calculate the value of fib(2): according to the definition, fib(2) requires summing fib(1) = 1 and fib(0) = 0, resulting in 1.

...

You can compare this with the recursion tree in the visualization panel, and it becomes easy to understand this process. A node must wait for the left child node to complete its calculation, then wait for the right child node to complete, and finally add the values of the two child nodes to obtain the value of the current node, which aligns with the definition fib(n) = fib(n-1) + fib(n-2).

From the perspective of tree structure, isn't it easy to understand the recursive calculation process? See how similar this fib function is to a binary tree traversal function. Therefore, the recursive tree abstracted from this function is a binary tree:

// Fibonacci sequence
int fib(int n) {
    if (n < 2) {
        return n;
    }
    return fib(n - 1)
         + fib(n - 2);
}

// Binary tree traversal function
void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    traverse(root.left);
    traverse(root.right);
}

Next, let's look at a slightly more complex recursive algorithm: the permutation problem.

Permutation Problem

You are given an input array nums with n distinct elements. You are asked to return all possible permutations of these elements.

For example, given nums = [1,2,3], the algorithm returns the following 6 permutations:

[1,2,3], [1,3,2],
[2,1,3], [2,3,1],
[3,1,2], [3,2,1]

The permutation and combination problem can have various variations, which we will explore in detail in Backtracking Algorithm: Mastering All Permutation and Combination Subset Problems. This article does not cover the code implementation but uses a visualization panel to understand the execution process of the permutation algorithm.

In middle school, we learned about permutations and combinations and solved similar problems. If you were to manually calculate the permutations of [1,2,3], how would you do it? Essentially, it's brute-force, but the process requires some organization:

Start by brute-forcing the first position, which can be any of 1, 2, 3, and we need to try each one.

If 1 is placed in the first position, the second position can only be 2 or 3.

If the second position is 2, the third position can only be 3, resulting in the first permutation [1,2,3].

If the second position is 3, the third position can only be 2, resulting in the second permutation [1,3,2].

Looking back, if 2 is placed in the first position, the second position can only be 1 or 3.

If the second position is 1, the third position can only be 3, resulting in the third permutation [2,1,3].

If the second position is 3, the third position can only be 1, resulting in the fourth permutation [2,3,1].

Looking back, if 3 is placed in the first position, the second position can only be 1 or 2.

If the second position is 1, the third position can only be 2, resulting in the fifth permutation [3,1,2].

If the second position is 2, the third position can only be 1, resulting in the sixth permutation [3,2,1].

Thus, we obtain all permutations of [1,2,3].

The brute-force process above can actually be abstracted into a recursive tree. Click on the visualization panel below and follow the instructions:

You don't need to fully understand the code now, just pay attention to the recursive part of the code:

class Solution {

    List<List<Integer>> res = new LinkedList<>();

    // Main function, input a set of unique numbers, return their permutations
    List<List<Integer>> permute(int[] nums) {
        // Record "path"
        LinkedList<Integer> track = new LinkedList<>();
        // Elements in the "path" will be marked as true to avoid reuse
        boolean[] used = new boolean[nums.length];
        
        backtrack(nums, track, used);
        return res;
    }

    // Path: recorded in track
    // Selection list: elements in nums that are not in track (used[i] is false)
    // Termination condition: all elements in nums appear in track
    void backtrack(int[] nums, LinkedList<Integer> track, boolean[] used) {
        // Trigger termination condition
        if (track.size() == nums.length) {
            res.add(new LinkedList(track));
            return;
        }

        for (int i = 0; i < nums.length; i++) {
            // Exclude invalid choices
            if (used[i]) {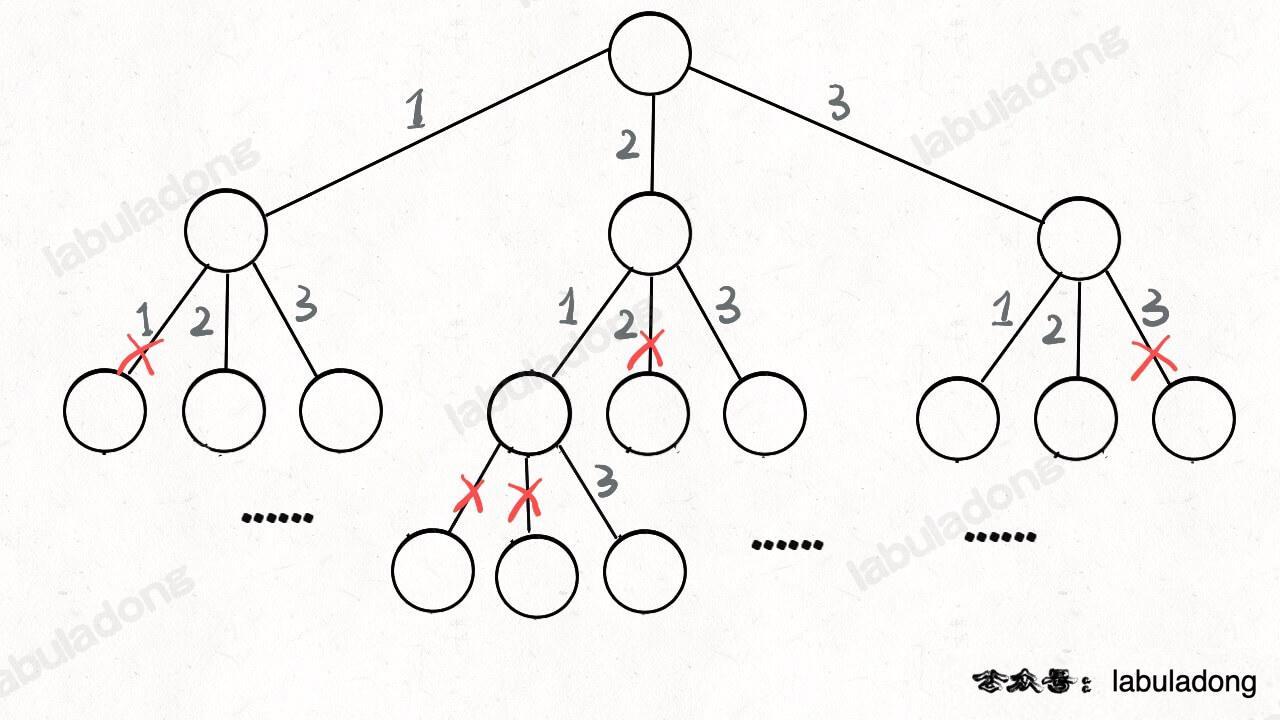

                // nums[i] is already in track, skip
                continue;
            }
            // Make a choice
            track.add(nums[i]);
            used[i] = true;
            // Enter the next level of the decision tree
            backtrack(nums, track, used);
            // Cancel the choice
            track.removeLast();
            used[i] = false;
        }
    }
}

#include <vector>
#include <list>

class Solution {

    std::vector<std::vector<int>> res;

public:
    // Main function, input a set of unique numbers, return their permutations
    std::vector<std::vector<int>> permute(std::vector<int>& nums) {
        
        backtrack(nums, track, used);
        return res;
    }

private:
    // Path: recorded in track
    // Selection list: elements in nums that are not in track (used[i] is false)
    // Termination condition: all elements in nums appear in track
    void backtrack(const std::vector<int>& nums, std::list<int>& track, std::vector<bool>& used) {
        // Trigger termination condition
        if (track.size() == nums.size()) {
            res.push_back(std::vector<int>(track.begin(), track.end()));
            return;
        }

        for (int i = 0; i < nums.size(); i++) {
            // Exclude invalid choices
            if (used[i]) {
                // nums[i] is already in track, skip
                continue;
            }
            // Make a choice
            track.push_back(nums[i]);
            used[i] = true;
            // Enter the next level of the decision tree
            backtrack(nums, track, used);
            // Cancel the choice
            track.pop_back();
            used[i] = false;
        }
    }
};

class Solution:
    def __init__(self):
        self.res = []

    # Main function, input a set of unique numbers, return their permutations
    def permute(self, nums):
        # Record "path"
        track = []
        # Elements in the "path" will be marked as true to avoid reuse
        used = [False] * len(nums)
        
        self.backtrack(nums, track, used)
        return self.res

    # Path: recorded in track
    # Selection list: elements in nums that are not in track (used[i] is false)
    # Termination condition: all elements in nums appear in track
    def backtrack(self, nums, track, used):
        # Trigger termination condition
        if len(track) == len(nums):
            self.res.append(track.copy())
            return

        for i in range(len(nums)):
            # Exclude invalid choices
            if used[i]: 

                # nums[i] is already in track, skip
                continue
            # Make a choice
            track.append(nums[i])
            used[i] = True
            # Enter the next level of the decision tree
            self.backtrack(nums, track, used)
            # Cancel the choice
            track.pop()
            used[i] = False

func permute(nums []int) [][]int {
    res := [][]int{}
    // Record "path"
    track := []int{}
    // Elements in the "path" will be marked as true to avoid reuse
    used := make([]bool, len(nums))
    
    backtrack(nums, track, used, &res)
    return res
}

// Path: recorded in track
// Selection list: elements in nums that are not in track (used[i] is false)
// Termination condition: all elements in nums appear in track
func backtrack(nums []int, track []int, used []bool, res *[][]int) {
    // Trigger termination condition
    if len(track) == len(nums) {
        temp := make([]int, len(track))
        copy(temp, track)
        *res = append(*res, temp)
        return
    }

    for i := 0; i < len(nums); i++ {
        // Exclude invalid choices
        if used[i] {
            // nums[i] is already in track, skip
            continue
        }
        // Make a choice
        track = append(track, nums[i])
        used[i] = true
        // Enter the next level of the decision tree
        backtrack(nums, track, used, res)
        // Cancel the choice
        track = track[:len(track)-1]
        used[i] = false
    }
}

var permute = function(nums) {
    // Main function, input a set of unique numbers, return their permutations
    let res = [];
    // Record "path"
    let track = [];
    // Elements in the "path" will be marked as true to avoid reuse
    let used = Array(nums.length).fill(false);

    // @visualize status(track)
    function backtrack(nums, track, used) {
        // Path: recorded in track
        // Selection list: elements in nums that are not in track (used[i] is false)
        // Termination condition: all elements in nums appear in track
        if (track.length === nums.length) {
            // Trigger termination condition
            res.push([...track]);
            return;
        }

        for (let i = 0; i < nums.length; i++) {
            // Exclude invalid choices
            if (used[i]) {
                // nums[i] is already in track, skip
                continue;
            }
            // Make a choice
            // @visualize choose(nums[i])
            track.push(nums[i]);
            used[i] = true;
            // Enter the next level of the decision tree
            backtrack(nums, track, used);
            // Cancel the choice
            // @visualize unchoose()
            track.pop();
            used[i] = false;
        }
    }

    backtrack(nums, track, used);
    return res;
};

Extracting the recursive part should reveal that this algorithm can be abstracted into a multi-branch tree:

// Permutations algorithm main structure
void backtrack(int[] nums, List<Integer> track) {
    if (track.size() == nums.length) {
        return;
    }
    for (int i = 0; i < nums.length; i++) {
        backtrack(nums, track);
    }
}

// Multi-fork tree traversal function
void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    for (TreeNode child : root.children) {
        traverse(child);
    }
}

You might have already sensed that the "tree" structure is a highly effective data structure. Abstracting a problem into a tree structure and then traversing this tree with code is the essence of recursion.

Two Mindsets for Writing Recursive Algorithms

Now that you know every recursive algorithm must be understood as a tree structure, let's go a step further: if you want to solve a problem with a recursive algorithm, how should you write the code?

It's actually quite simple. When writing a recursive algorithm, there are only two possible mindsets. Try applying both, and one will surely work:

One is the "traversal" mindset, and the other is the "problem decomposition" mindset.

In the examples discussed above, although both are abstracted into a recursive tree, the Fibonacci sequence uses the "problem decomposition" mindset, while the full permutation uses the "traversal" mindset.

Problem Decomposition Mindset

Consider the Fibonacci sequence problem; each node on the recursive tree is essentially the solution to a sub-problem. How is fib(5) calculated? The root node fib(5) asks its left and right child nodes fib(4) and fib(3) for their values, and then sums them:

Here lies a process of problem decomposition: breaking a larger problem fib(5) into smaller problems fib(4) and fib(3), and then using the solutions of the sub-problems to derive the solution to the original problem. We can call this mindset "problem decomposition".

For example, the recursive function fib for the Fibonacci sequence has a clear definition, and the algorithm uses this definition:

// Definition: Input a non-negative integer n, return the nth number in the Fibonacci sequence
int fib(int n) {
    if (n < 2) {
        return n;
    }
    // Use the definition to calculate the first two Fibonacci numbers (subproblems)
    int fib_n_1 = fib(n - 1);
    int fib_n_2 = fib(n - 2);

    // Use the answers of subproblems to calculate the original problem
    return fib_n_1 + fib_n_2;
}

Let's consider a simple example, such as calculating the maximum depth of a binary tree, LeetCode problem 104 "Maximum Depth of Binary Tree":

104. Maximum Depth of Binary Tree | LeetCode |  🟢

Given the root of a binary tree, return its maximum depth.

A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1:

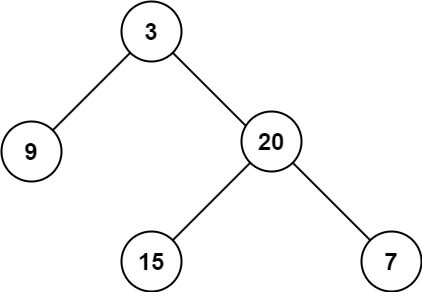
Input: root = [3,9,20,null,null,15,7]
Output: 3

Example 2:

Input: root = [1,null,2]
Output: 2

Constraints:

• The number of nodes in the tree is in the range [0, 104].
• -100 <= Node.val <= 100

The problem is from LeetCode 104. Maximum Depth of Binary Tree.

This problem can be solved by decomposing the problem: to calculate the maximum depth of the entire tree, first calculate the maximum depth of the left and right subtrees, take the maximum of the two values and add one, which gives the maximum depth of the entire tree.

We can then give the maxDepth function a clear definition: input a node of a binary tree, and the function returns the maximum depth of the binary tree with this node as the root.

Then, you can obtain a recursive formula similar to the Fibonacci sequence:

$$maxDepth(root) = \begin{cases} 0 & \text{if } root = null \\ max(maxDepth(root.left), maxDepth(root.right)) + 1 & \text{otherwise} \end{cases}$$

// Divide and Conquer Idea
class Solution {
    // Definition: Given a node, return the maximum depth of the binary tree rooted at that node
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int leftMax = maxDepth(root.left);
        int rightMax = maxDepth(root.right);
        // Derive the maximum depth of the original binary tree
        // based on the maximum depth of the left and right
        return 1 + Math.max(leftMax, rightMax);
    }
}

// Divide and Conquer Idea
class Solution {
public:
    // Definition: Given a node, return the maximum depth of the binary tree rooted at that node
    int maxDepth(TreeNode* root) {
        if (root == nullptr) {
            return 0;
        }
        int leftMax = maxDepth(root->left);
        int rightMax = maxDepth(root->right);
        // Derive the maximum depth of the original binary tree
        // based on the maximum depth of the left and right
        return 1 + std::max(leftMax, rightMax);
    }
};

# Divide and Conquer Idea
class Solution:
    # Definition: Given a node, return the maximum depth of the binary tree rooted at that node
    def maxDepth(self, root: TreeNode) -> int:
        if root is None:
            return 0
        leftMax = self.maxDepth(root.left)
        rightMax = self.maxDepth(root.right)
        # Derive the maximum depth of the original binary
        # tree based on the maximum depth of the left and
        return 1 + max(leftMax, rightMax)

// Divide and Conquer Idea
func maxDepth(root *TreeNode) int {
    // Definition: Given a node, return the maximum depth of the binary tree rooted at that node
    if root == nil {
        return 0
    }
    leftMax := maxDepth(root.Left)
    rightMax := maxDepth(root.Right)
    // Derive the maximum depth of the original binary tree
    // based on the maximum depth of the left and right
    return 1 + max(leftMax, rightMax)
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

// Divide and Conquer Idea
// Definition: Given a node, return the maximum depth of the binary tree rooted at that node
var maxDepth = function(root) {
    if (root === null) {
        return 0;
    }
    var leftMax = maxDepth(root.left);
    var rightMax = maxDepth(root.right);
    // Derive the maximum depth of the original binary tree
    // based on the maximum depth of the left and right
    return 1 + Math.max(leftMax, rightMax);
};

For this problem, I have also provided a visual panel to demonstrate the execution process of the recursive function. The orange represents the real binary tree structure, while the pink represents the abstracted recursive tree structure, where the value of the parent node is the larger value of the left and right child nodes plus one.

Now you should understand the "decomposition" approach. Next, let's look at another way to write recursive algorithms.

Traversal Approach

Combine with the visual panel to look at the permutation problem:

The nodes on the recursive tree do not have an explicit meaning, they only record some choices made previously. All permutations are the results on all leaf nodes. This approach is called "traversal."

For example, in the permutation problem, you don't need to fully understand the permutation code right now, just note that the backtrack function has no return value and no explicit definition. It acts like a for loop, simply traversing the recursive tree and collecting results from the leaf nodes:

// Permutations algorithm main structure

// Global variable, store the state of backtrack function traversal
List<List<Integer>> res = new LinkedList<>();
List<Integer> track = new LinkedList<>();

// Recursion tree traversal function
void backtrack(int[] nums, List<Integer> track) {
    if (track.size() == nums.length) {
        // Reach the leaf node, collect the result
        res.add(new LinkedList<>(track));
        return;
    }
    for (int i = 0; i < nums.length; i++) {
        // Make a choice
        track.add(nums[i]);

        backtrack(nums, track);

        // Undo the choice
        track.removeLast();
    }
}

Can you distinguish the difference between the two thinking modes of "traversal" and "problem decomposition"?

Let's look at LeetCode problem 104 "Maximum Depth of Binary Tree". We can use the "traversal" thinking mode to write a solution by using the standard binary tree traversal function traverse to go through the entire tree. During the traversal, we update the maximum depth, ensuring that once all nodes are traversed, the maximum depth of the entire tree is determined:

// Traversal Idea
class Solution {

    int depth = 0;
    int res = 0;

    public int maxDepth(TreeNode root) {
        traverse(root);
        return res;
    }

    // Traverse the binary tree
    void traverse(TreeNode root) {
        if (root == null) {
            return;
        }

        // Pre-order traversal position (entering a node) increases depth
        depth++;
        // Record the maximum depth during traversal
        if (root.left == null && root.right == null) {
            res = Math.max(res, depth);
        }
        traverse(root.left);
        traverse(root.right);

        // Post-order traversal position (leaving a node) decreases depth
        depth--;
    }
}

// Traversal Idea
class Solution {

    int depth = 0;
    int res = 0;

public:
    int maxDepth(TreeNode* root) {
        traverse(root);
        return res;
    }

    // Traverse the binary tree
    void traverse(TreeNode* root) {
        if (root == nullptr) {
            return;
        }

        // Pre-order traversal position (entering a node) increases depth
        depth++;
        // Record the maximum depth during traversal
        if (root->left == nullptr && root->right == nullptr) {
            res = std::max(res, depth);
        }
        traverse(root->left);
        traverse(root->right);

        // Post-order traversal position (leaving a node) decreases depth
        depth--;
    }
};

# Traversal Idea
class Solution:

    def __init__(self):
        self.depth = 0
        self.res = 0

    def maxDepth(self, root: TreeNode) -> int:
        self.traverse(root)
        return self.res

    # Traverse the binary tree
    def traverse(self, root: TreeNode):
        if root is None:
            return

        # Pre-order traversal position (entering a node) increases depth
        self.depth += 1
        # Record the maximum depth during traversal
        if root.left is None and root.right is None:
            self.res = max(self.res, self.depth)
        self.traverse(root.left)
        self.traverse(root.right)

        # Post-order traversal position (leaving a node) decreases depth
        self.depth -= 1

func maxDepth(root *TreeNode) int {
    var depth, res int
    traverse(root, &depth, &res)
    return res
}

// Traverse the binary tree
func traverse(root *TreeNode, depth *int, res *int) {
    if root == nil {
        return
    }

    // Pre-order traversal position (entering a node) increases depth
    *depth++
    // Record the maximum depth during traversal
    if root.Left == nil && root.Right == nil {
        *res = max(*res, *depth)
    }
    traverse(root.Left, depth, res)
    traverse(root.Right, depth, res)

    // Post-order traversal position (leaving a node) decreases depth
    *depth--
}

// Traversal Idea
func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

// Traversal Idea
var maxDepth = function(root) {
    let depth = 0;
    let res = 0;

    // Traverse the binary tree
    var traverse = function(node) {
        if (node === null) {
            return;
        }

        // Pre-order traversal position (entering a node) increases depth
        depth++;
        // Record the maximum depth during traversal
        if (node.left === null && node.right === null) {
            res = Math.max(res, depth);
        }
        traverse(node.left);
        traverse(node.right);

        // Post-order traversal position (leaving a node) decreases depth
        depth--;
    };

    traverse(root);
    return res;
};

For this problem, I also provided a visual panel to display the execution process of the recursive function. The orange part represents the actual binary tree structure, and the pink part represents the abstract recursive tree structure. Essentially, traverse is a standard binary tree traversal function that records the current depth during traversal and updates the maximum depth upon reaching a leaf node.

Summary

This article first uses the Fibonacci sequence and permutation problems for recursion visualization, arguing that recursion algorithms must be understood from the "tree" perspective.

Then, it summarizes the two thinking modes for writing recursive algorithms: the "problem decomposition" approach and the "traversal" approach. The solution for the Fibonacci sequence presented in the article is based on the "problem decomposition" approach, while the solution for permutations uses the "traversal" approach.

Some problems can be approached using both thinking modes, such as LeetCode problem 104 "Maximum Depth of Binary Tree". Both the "problem decomposition" and "traversal" approaches can solve it with the same efficiency, though the code may look significantly different.

The ultimate goal of the above discussion is to enable you to write recursive algorithms smoothly by referring to the following steps:

1. First, can this problem be abstracted into a tree structure? If so, a recursive algorithm is needed.

2. If a recursive algorithm is needed, consider the two thinking modes of "traversal" and "problem decomposition" to determine which is more suitable for the problem.

3. If using the "problem decomposition" mode, clearly define the recursive function and use this definition to break down the problem and derive the solution from subproblems; if using the "traversal" mode, use a non-returning recursive function to purely traverse the recursive tree and collect the target results.

In fact, the "problem decomposition" thinking mode corresponds to the Dynamic Programming Algorithm and Divide and Conquer Algorithm to be explained later, while the "traversal" mode corresponds to the DFS/Backtracking Algorithm to be explained later.

In the Binary Tree Exercises Chapter, I specifically solve all binary tree-related problems using these two thinking modes. Once you understand binary trees, these recursive algorithms become very straightforward.