Sliding Window Algorithm Code Template

labuladongOriginalAbout 6697 words

This article will resolve

LeetCode	Difficulty
3. Longest Substring Without Repeating Characters	🟠
438. Find All Anagrams in a String	🟠
567. Permutation in String	🟠
76. Minimum Window Substring	🔴

In the previous article Double Pointer Techniques, we talked about some simple double pointer tricks for arrays. In this article, we will discuss a slightly more complex technique: the sliding window.

The sliding window can be seen as a fast and slow double pointer. One pointer moves fast, the other slow, and the part between them is the window. The sliding window algorithm is mainly used to solve subarray problems, such as finding the longest or shortest subarray that meets certain conditions.

You can open the visualization panel below. Click the line while (right < s.length) multiple times to see how the window moves step by step:

Algorithm Visualization

This article will give you a template that helps you write correct solutions easily. Each problem also has a visualization panel to help you better understand how the window slides.

Sliding Window Framework Overview

If you use brute-force, you need nested for-loops to go through all subarrays. The time complexity is $O(N^2)$ :

for (int i = 0; i < nums.length; i++) {
    for (int j = i; j < nums.length; j++) {
        // nums[i, j] is a subarray
    }
}

The sliding window idea is simple: keep a window, move it step by step, and update the answer. The general logic is:

// The range [left, right) is the window
int left = 0, right = 0;

while (right < nums.size()) {
    // Expand the window
    window.addLast(nums[right]);
    right++;
    
    while (window needs shrink) {
        // Shrink the window
        window.removeFirst(nums[left]);
        left++;
    }
}

If you use this sliding window framework, the time complexity is $O(N)$ , which is much faster than the brute-force solution.

Why is it $O(N)$ ?

Some of you may ask, "Isn't there a nested while loop? Why is the complexity $O(N)$ ?"

Simply put, the pointers left and right never move backward. They only move forward. So, each element in the string/array is added to the window once, and removed once. No element is added or removed more than once, so the time complexity is proportional to the length of the string/array.

But in the nested for-loop brute-force solution, j moves backward, so some elements are counted many times. That's why its time complexity is $O(N^2)$ .

If you want to learn more about time and space complexity, check my article Guide to Analyzing Algorithm Complexity.

Can sliding window really list all subarrays in $O(N)$ time?

Actually, this is a mistake. Sliding window cannot list all substrings. If you want to go through all substrings, you have to use the nested for-loops.

But for some problems, you don't need to check all substrings to find the answer. In these cases, the sliding window is a good template to make the solution faster and avoid extra calculations.

That's why in The Essence of Algorithms, I put sliding window in the category of "smart enumeration".

What really confuses people are the details. For example, how to add new elements to the window, when to shrink the window, and when to update the result. Even if you know these, the code may still have bugs, and it's not easy to debug.

So today I will give you a sliding window code template. I will even add print debug statements for you. Next time you see a related problem, just recall this template and change three places. This will help you avoid bugs.

Since most examples in this article are substring problems, and a string is just an array, the input will be a string. When you solve problems, adapt as needed:

java

// Pseudocode framework of sliding window algorithm
void slidingWindow(String s) {
    // Use an appropriate data structure to record the data in the
    // window, which can vary according to the specific scenario
    // For example, if I want to record the frequency
    // of elements in the window, I would use a map
    // If I want to record the sum of elements in the window, I could just use an int
    Object window = ...
    
    int left = 0, right = 0;
    while (right < s.length()) {
        // c is the character that will be added to the window
        char c = s[right];
        window.add(c)
        // Expand the window
        right++;
        // Perform a series of updates to the data within the window
        ...

        // *** Position of debug output ***
        // Note that in the final solution code, do not use print
        // Because IO operations are time-consuming and may cause timeouts
        printf("window: [%d, %d)\n", left, right);
        // ***********************

        // Determine whether the left side of the window needs to shrink
        while (left < right && window needs shrink) {
            // d is the character that will be removed from the window
            char d = s[left];
            window.remove(d)
            // Shrink the window
            left++;
            // Perform a series of updates to the data within the window
            ...
        }
    }
}

cpp

// Pseudocode framework of sliding window algorithm
void slidingWindow(string s) {
    // Use an appropriate data structure to record the data
    // in the window, varying with the specific scenario
    // For instance, if I want to record the frequency
    // of elements in the window, I would use a map
    // If I want to record the sum of elements in the window, I can simply use an int
    auto window = ...

    int left = 0, right = 0;
    while (right < s.size()) {
        // c is the character that will be entering the window
        char c = s[right];
        window.add(c);
        // Expand the window
        right++;

        // Perform a series of updates to the data within the window
        ...

        // *** position of debug output ***
        printf("window: [%d, %d)\n", left, right);
        // Note that printing should be avoided in the final solution code
        // Because IO operations are time-consuming and may cause timeouts

        // Determine whether the left side of the window needs to shrink
        while (window needs shrink) {
            // d is the character that will be removed from the window
            char d = s[left];
            window.remove(d);
            // Shrink the window
            left++;

            // Perform a series of updates to the data within the window
            ...
        }
    }
}

python

# Pseudocode framework for sliding window algorithm
def slidingWindow(s: str):
    # Use an appropriate data structure to record the data in
    # the window, which can vary depending on the scenario
    # For example, if I want to record the frequency
    # of elements in the window, I would use a map
    # If I want to record the sum of elements in the window, I could just use an int
    window = ...

    left, right = 0, 0
    while right < len(s):
        # c is the character that will be added to the window
        c = s[right]
        window.add(c)
        # Expand the window
        right += 1
        # Perform a series of updates on the data within the window
        ...

        # *** position for debug output ***
        # Note that you should not print in the final solution code
        # because IO operations are time-consuming and may cause timeouts
        # print(f"window: [{left}, {right})")
        # ***********************

        # Determine whether the left side of the window needs to be contracted
        while left < right and window needs shrink:
            # d is the character that will be removed from the window
            d = s[left]
            window.remove(d)
            # Shrink the window
            left += 1
            # Perform a series of updates on the data within the window
            ...

// Pseudocode framework for sliding window algorithm
func slidingWindow(s string) {
    // Use an appropriate data structure to record the data in the
    // window, which can vary according to the specific scenario
    // For example, if I want to record the frequency of elements in the window, I use a map
    // If I want to record the sum of elements in the window, I can just use an int
    var window = ...

    left, right := 0, 0
    for right < len(s) {
        // c is the character to be moved into the window
        c := rune(s[right])
        window[c]++
        // Expand the window
        right++
        // Perform a series of updates to the data within the window
        ...

        // *** debug output location ***
        // Note that in the final solution code, do not print
        // Because IO operations are time-consuming and may cause timeouts
        fmt.Println("window: [",left,", ",right,")")
        // ***********************

        // Determine whether the left window needs to shrink
        for left < right && window needs shrink {
            // d is the character to be moved out of the window
            d := rune(s[left])
            window[d]--
            // Shrink the window
            left++
            // Perform a series of updates to the data within the window
            ...
        }
    }
}

javascript

// Pseudocode framework for sliding window algorithm
var slidingWindow = function(s) {
    // Use an appropriate data structure to record the data in
    // the window, which can vary according to the scenario
    // For example, if I want to record the frequency of elements in the window, I use a map
    // If I want to record the sum of the elements in the window, I can just use an int
    var window = ...;

    var left = 0, right = 0;
    while (right < s.length) {
        // c is the character that will be moved into the window
        var c = s[right];
        window.add(c);
        // Expand the window
        right++;
        // Perform a series of updates on the data within the window
        ...

        // *** debug output position ***
        // Note that in the final solution code, do not print
        // Because IO operations are time-consuming and may cause timeouts
        console.log("window: [%d, %d)\n", left, right);
        // *********************

        // Determine whether the left side of the window needs to shrink
        while (window needs shrink) {
            // d is the character that will be moved out of the window
            var d = s[left];
            window.remove(d);
            // Shrink the window
            left++;
            // Perform a series of updates on the data within the window
            ...
        }
    }
};

There are two places in the template marked with .... These are where you update the data for the window. In a real problem, just fill in your logic here. These two places are for expanding and shrinking the window, and you will see that their logic is almost the same, just opposite.

With this template, if you get a substring or subarray problem, just answer these three questions:

When should you move right to expand the window? What data should you update when adding a character to the window?
When should you stop expanding and start moving left to shrink the window? What data should you update when removing a character from the window?
When should you update the result?

If you can answer these questions, you can use the sliding window technique for the problem.

Next, we'll use this template to solve four LeetCode problems. For the first problem, I will explain the ideas in detail. For the others, just use the template and solve them quickly.

1. Minimum Window Substring

Let's look at LeetCode problem 76: "Minimum Window Substring" (Hard):

76. Minimum Window Substring | LeetCode | 🔴

Given two strings s and t of lengths m and n respectively, return the minimum window substring of s such that every character in t (including duplicates) is included in the window. If there is no such substring, return the empty string "".

The testcases will be generated such that the answer is unique.

Example 1:

Input: s = "ADOBECODEBANC", t = "ABC"
Output: "BANC"
Explanation: The minimum window substring "BANC" includes 'A', 'B', and 'C' from string t.

Example 2:

Input: s = "a", t = "a"
Output: "a"
Explanation: The entire string s is the minimum window.

Example 3:

Input: s = "a", t = "aa"
Output: ""
Explanation: Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.

Constraints:

m == s.length
n == t.length
1 <= m, n <= 10⁵
s and t consist of uppercase and lowercase English letters.

Follow up: Could you find an algorithm that runs in O(m + n) time?

The problem is from LeetCode 76. Minimum Window Substring.

You need to find a substring in S (source) that contains all the letters from T (target), and this substring must be the shortest one among all possible substrings.

If we use a brute-force solution, the code looks like this:

for (int i = 0; i < s.length(); i++)
    for (int j = i + 1; j < s.length(); j++)
        if s[i:j] contains all letters in t:
            update answer

This idea is simple, but the time complexity is definitely more than $O(N^2)$ , which is not good.

The sliding window algorithm works like this:

We use two pointers, left and right, to define a window in string S. Initialize left = right = 0. The range [left, right) is a left-closed, right-open window.

Why use "left-closed, right-open" interval?

In theory, you can use any kind of interval, but using left-closed, right-open is the most convenient.

When you set left = right = 0, the interval [0, 0) has no elements. But if you move right one step, [0, 1) now contains element 0.

If you use both ends open, moving right to (0, 1) still has no element. If you use both ends closed, [0, 0] already contains one element at the start. These two cases will make boundary handling harder.

First, keep moving the right pointer to expand the window [left, right), until the window contains all the characters in T.
Then, stop moving right, and start moving left to shrink the window [left, right), until the window no longer contains all characters in T. Each time you move left, update the answer.
Repeat steps 2 and 3 until right reaches the end of string S.

This idea is not hard. Step 2 is to find a "valid solution"; step 3 is to optimize this "valid solution" to find the optimal answer, which is the shortest substring. The left and right pointers move back and forth, making the window grow and shrink, just like a caterpillar moving along—this is why it's called a "sliding window."

Let's use some pictures for understanding. needs and window are like counters. needs records the count of each character in T, and window records the count of each character in the current window.

Initial state:

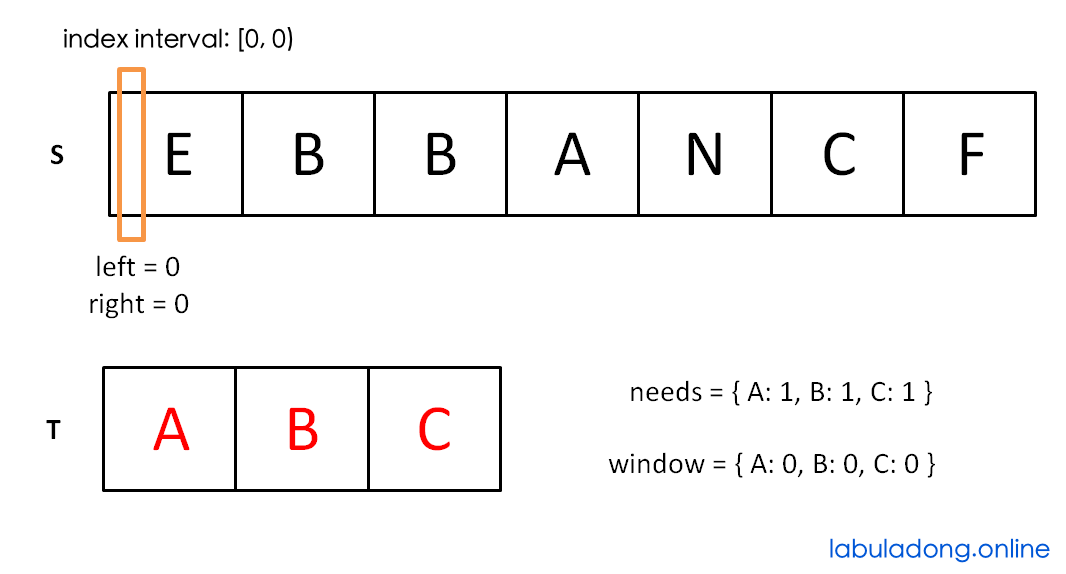
Move right until the window [left, right) contains all characters in T:

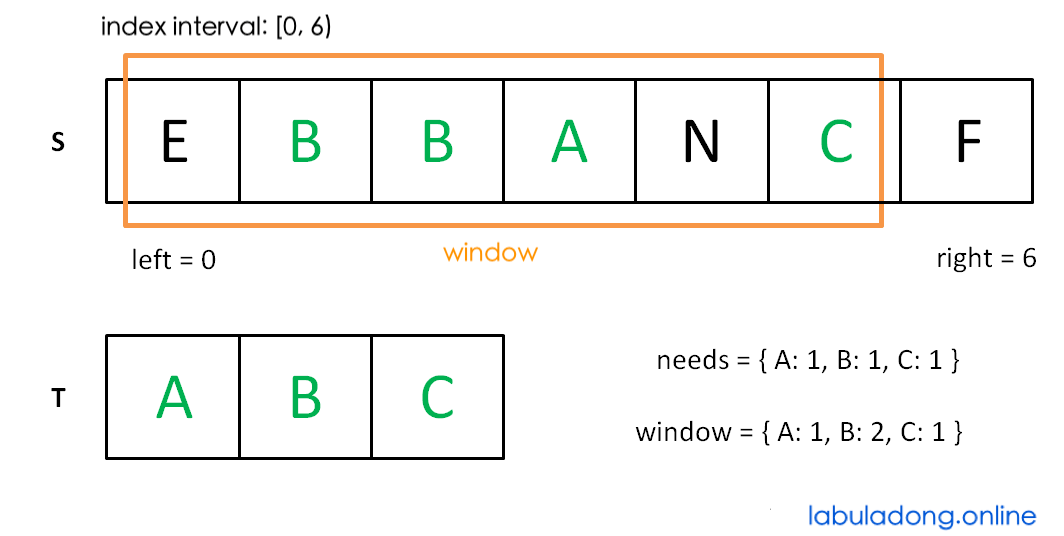
Now move left to shrink the window [left, right):

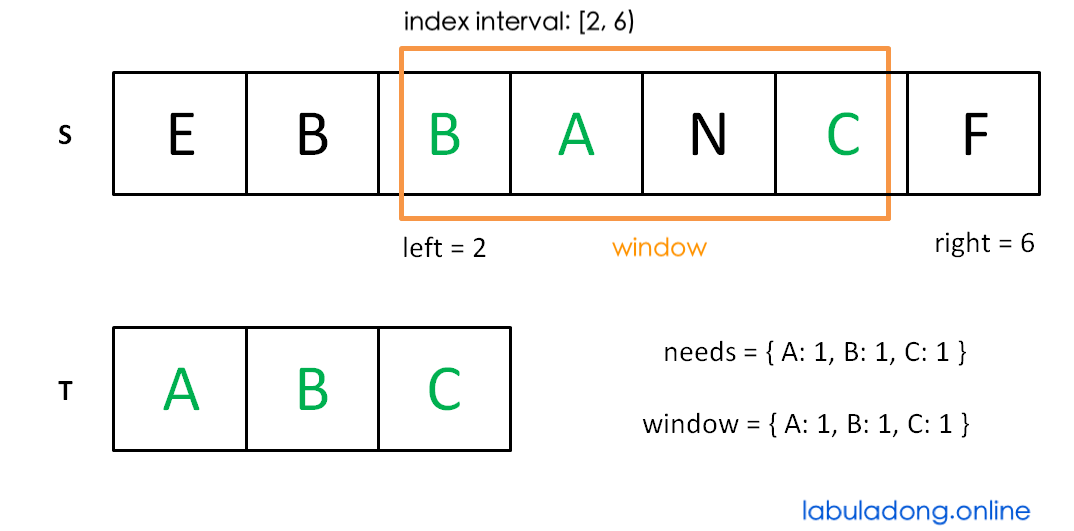
Stop moving left when the window no longer meets the requirement:

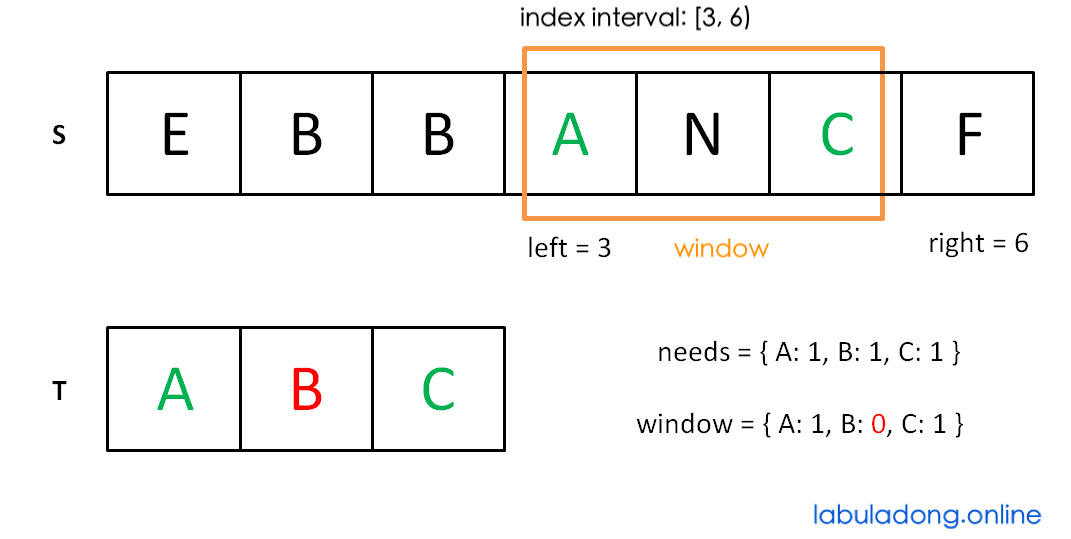
Then repeat: move right, then move left... until right reaches the end of S. The algorithm ends.

If you understand this process, congratulations, you have mastered the sliding window algorithm. Now let's look at the sliding window code template:

First, initialize two hash maps, window and need, to record the characters in the window and the characters you need:

// Count of characters in window
HashMap<Character, Integer> window = new HashMap<>();
// Count of required characters
HashMap<Character, Integer> need = new HashMap<>();
for (int i = 0; i < t.length(); i++) {
    char c = t.charAt(i);
    need.put(c, need.getOrDefault(c, 0) + 1);
}

Then, use left and right as the two ends of the window. Remember, [left, right) is left-closed, right-open, so at the start the window is empty:

int left = 0, right = 0;
int valid = 0;
while (right < s.length()) {
    // c is the character going into the window
    char c = s.charAt(right);
    // Move right to expand window
    right++;
    // Update data inside the window
    ...
}

The valid variable counts how many characters in the window meet the need requirement. If valid equals need.size(), the window is valid and covers all characters in T.

Now, using this template, just think about these questions:

When should you move right to expand the window? When you add a character to the window, what should you update?
When should you stop expanding and start moving left to shrink the window? When you remove a character, what should you update?
Should you update the result when expanding or shrinking the window?

If a character enters the window, increase its count in window. If a character leaves, decrease its count. When valid meets the requirement, start shrinking the window. Update the answer when shrinking.

Here is the complete code:

java

class Solution {
    public String minWindow(String s, String t) {
        Map<Character, Integer> need = new HashMap<>();
        Map<Character, Integer> window = new HashMap<>();
        for (char c : t.toCharArray()) {
            need.put(c, need.getOrDefault(c, 0) + 1);
        }

        int left = 0, right = 0;
        int valid = 0;
        // record the start index and length of the minimum coverage substring
        int start = 0, len = Integer.MAX_VALUE;
        while (right < s.length()) {
            // c is the character that will be added to the window
            char c = s.charAt(right);
            // expand the window
            right++;
            // perform a series of updates to the data inside the window
            if (need.containsKey(c)) {
                window.put(c, window.getOrDefault(c, 0) + 1);
                if (window.get(c).equals(need.get(c)))
                    valid++;
            }

            // determine whether the left side of the window needs to be contracted
            while (valid == need.size()) {
                // update the minimum coverage substring here
                if (right - left < len) {
                    start = left;
                    len = right - left;
                }
                // d is the character that will be removed from the window
                char d = s.charAt(left);
                // shrink the window
                left++;
                // perform a series of updates to the data inside the window
                if (need.containsKey(d)) {
                    if (window.get(d).equals(need.get(d)))
                        valid--;
                    window.put(d, window.get(d) - 1);
                }                    
            }
        }
        // return the minimum coverage substring
        return len == Integer.MAX_VALUE ? "" : s.substring(start, start + len);
    }
}

cpp

class Solution {
public:
    string minWindow(string s, string t) {
        unordered_map<char, int> need, window;
        for (char c : t) {
            need[c]++;
        }

        int left = 0, right = 0;
        // record the number of characters in window that meet the need condition
        int valid = 0;
        // record the start index and length of the minimum covering substring
        int start = 0, len = INT_MAX;
        while (right < s.size()) {
            // c is the character to be moved into the window
            char c = s[right];
            // expand the window
            right++;
            // perform a series of updates to the data within the window
            if (need.count(c)) {
                window[c]++;
                if (window[c] == need[c])
                    valid++;
            }

            // determine whether the left window needs to be shrinked
            while (valid == need.size()) {
                // update the minimum covering substring here
                if (right - left < len) {
                    start = left;
                    len = right - left;
                }
                // d is the character to be moved out of the window
                char d = s[left];
                // shrink the window
                left++;
                // perform a series of updates to the data within the window
                if (need.count(d)) {
                    if (window[d] == need[d])
                        valid--;
                    window[d]--;
                }
            }
        }
        // return the minimum covering substring
        return len == INT_MAX ? "" : s.substr(start, len);
    }
};

python

class Solution:
    def minWindow(self, s: str, t: str) -> str:
        need, window = {}, {}
        for c in t:
            need[c] = need.get(c, 0) + 1

        left = 0
        right = 0
        valid = 0
        # record the start index and length of the minimum covering substring
        start = 0
        length = float('inf')
        while right < len(s):
            # c is the character that will be added to the window
            c = s[right]
            # expand the window
            right += 1
            # perform a series of updates to the data within the window
            if c in need:
                window[c] = window.get(c, 0) + 1
                if window[c] == need[c]:
                    valid += 1

            # determine whether the left side of the window needs to be contracted
            while valid == len(need): 
                # update the minimum covering substring here
                if right - left < length:
                    start = left
                    length = right - left
                # d is the character that will be removed from the window
                d = s[left]
                # shrink the window
                left += 1
                # perform a series of updates to the data within the window
                if d in need:
                    if window[d] == need[d]:
                        valid -= 1
                    window[d] -= 1

        # return the minimum covering substring
        return "" if length == float('inf') else s[start: start + length]

func minWindow(s string, t string) string {
    need, window := make(map[byte]int), make(map[byte]int)
    for i := range t {
        need[t[i]]++
    }

    left, right := 0, 0
    valid := 0
    // record the start index and length of the minimum covering substring
    start, length := 0, math.MaxInt32
    for right < len(s) {
        // c is the character that will be added to the window
        c := s[right]
        // expand the window
        right++
        // perform a series of updates to the data inside the window
        if _, ok := need[c]; ok {
            window[c]++
            if window[c] == need[c] {
                valid++
            }
        }

        // determine whether the left side of the window needs to be contracted
        for valid == len(need) {
            // update the minimum covering substring here
            if right - left < length {
                start = left
                length = right - left
            }
            // d is the character that will be removed from the window
            d := s[left]
            // shrink the window
            left++
            // perform a series of updates to the data inside the window
            if _, ok := need[d]; ok {
                if window[d] == need[d] {
                    valid--
                }
                window[d]--
            }
        }
    }
    // return the minimum covering substring
    if length == math.MaxInt32 {
        return ""
    }
    return s[start : start+length]
}

javascript

var minWindow = function(s, t) {
    let need = {}, window = {};
    for (let c of t) {
        need[c] = (need[c] || 0) + 1;
    }

    let left = 0, right = 0;
    let valid = 0;
    // record the start index and length of the minimum covering substring
    let start = 0, len = Infinity;
    while (right < s.length) {
        // c is the character to be moved into the window
        let c = s[right];
        // expand the window
        right++;
        // perform a series of updates to the data inside the window
        if (need[c]) {
            window[c] = (window[c] || 0) + 1;
            if (window[c] === need[c]) {
                valid++;
            }
        }

        // determine whether the left side of the window needs to shrink
        while (valid === Object.keys(need).length) {
            // update the minimum covering substring here
            if (right - left < len) {
                start = left;
                len = right - left;
            }
            // d is the character to be moved out of the window
            let d = s[left];
            // shrink the window
            left++;
            // perform a series of updates to the data inside the window
            if (need[d]) {
                if (window[d] === need[d]) {
                    valid--;
                }
                window[d]--;
            }
        }
    }
    // return the minimum covering substring
    return len === Infinity ? "" : s.substring(start, start + len);
};

You can open the panel below and click the line while (right < s.length) several times to see how the sliding window [left, right) moves:

Algorithm Visualization

Note for Java users

Be careful when comparing Java wrapper classes like Integer and String. You should use the equals method instead of ==, or you may get errors. For example, don't write window.get(d) == need.get(d), but use window.get(d).equals(need.get(d)). This applies to the following problems as well.

In the code above, when a character's count in window meets the need in need, update valid to show that one more character meets the requirement. Notice that the updates for adding and removing characters are symmetric.

When valid == need.size(), all characters in T are included, and you have a valid window. Now you should start shrinking the window to try to find the smallest one.

When moving left to shrink the window, every window is a valid answer, so update the result during the shrinking phase to find the shortest one.

Now you should fully understand this template. The sliding window algorithm is not hard, just some details to be careful with. Whenever you see a sliding window problem, use this template and your code will be bug-free and easy to write.

Let's use this template to quickly solve a few more problems. Once you see the description, you will know what to do.

2. Permutation in String

This is LeetCode Problem 567 "Permutation in String", medium level:

567. Permutation in String | LeetCode | 🟠

Given two strings s1 and s2, return true if s2 contains a permutation of s1, or false otherwise.

In other words, return true if one of s1's permutations is the substring of s2.

Example 1:

Input: s1 = "ab", s2 = "eidbaooo"
Output: true
Explanation: s2 contains one permutation of s1 ("ba").

Example 2:

Input: s1 = "ab", s2 = "eidboaoo"
Output: false

Constraints:

1 <= s1.length, s2.length <= 10⁴
s1 and s2 consist of lowercase English letters.

The problem is from LeetCode 567. Permutation in String.

Note that the input s1 can contain duplicate characters, so this problem is not easy.

This is a typical sliding window problem. Basically, you are given a string S and a string T. You need to check if there is a substring in S with the same length as T, and that substring contains all characters in T.

First, copy and paste the sliding window template code. Then, just make a few changes to answer the questions mentioned earlier, and you can solve this problem:

java

class Solution {
    // determine if there is a permutation of t in s
    public boolean checkInclusion(String t, String s) {
        Map<Character, Integer> need = new HashMap<>();
        Map<Character, Integer> window = new HashMap<>();
        for (char c : t.toCharArray()) need.put(c, need.getOrDefault(c, 0) + 1);

        int left = 0, right = 0;
        int valid = 0;
        while (right < s.length()) {
            char c = s.charAt(right);
            right++;
            // update the data inside the window
            if (need.containsKey(c)) {
                window.put(c, window.getOrDefault(c, 0) + 1);
                if (window.get(c).equals(need.get(c)))
                    valid++;
            }

            // check if the left side of the window needs to shrink
            while (right - left >= t.length()) {
                // check here if a valid substring is found
                if (valid == need.size())
                    return true;
                char d = s.charAt(left);
                left++;
                // update the data inside the window
                if (need.containsKey(d)) {
                    if (window.get(d).equals(need.get(d)))
                        valid--;
                    window.put(d, window.get(d) - 1);
                }
            }
        }
        // no valid substring found
        return false;
    }
}

cpp

class Solution {
public:
    // determine if there is a permutation of t in s
    bool checkInclusion(string t, string s) {
        unordered_map<char, int> need, window;
        for (char c : t) need[c]++;

        int left = 0, right = 0;
        int valid = 0;
        while (right < s.size()) {
            char c = s[right];
            right++;
            // update the data inside the window
            if (need.count(c)) {
                window[c]++;
                if (window[c] == need[c])
                    valid++;
            }

            // check if the left side of the window needs to shrink
            while (right - left >= t.size()) {
                // check here if a valid substring is found
                if (valid == need.size())
                    return true;
                char d = s[left];
                left++;
                // update the data inside the window
                if (need.count(d)) {
                    if (window[d] == need[d])
                        valid--;
                    window[d]--;
                }
            }
        }
        // no valid substring found
        return false;
    }
};

python

class Solution:
    # determine if there is a permutation of t in s
    def checkInclusion(self, t: str, s: str) -> bool:
        need = {}
        window = {}
        for c in t:
            need[c] = need.get(c, 0) + 1

        left = 0
        right = 0
        valid = 0
        while right < len(s):
            c = s[right]
            right += 1
            # update the data inside the window
            if c in need:
                window[c] = window.get(c, 0) + 1
                if window[c] == need[c]:
                    valid += 1

            # check if the left side of the window needs to shrink
            while right - left >= len(t):
                # check here if a valid substring is found
                if valid == len(need):
                    return True
                d = s[left]
                left += 1
                # update the data inside the window
                if d in need:
                    if window[d] == need[d]:
                        valid -= 1
                    window[d] -= 1

        # no valid substring found
        return False

func checkInclusion(t string, s string) bool {
    // determine if there is a permutation of t in s
    need := make(map[rune]int)
    window := make(map[rune]int)
    for _, c := range t {
        need[c]++
    }

    left, right := 0, 0
    valid := 0
    for right < len(s) {
        c := rune(s[right])
        right++
        // update the data inside the window
        if need[c] > 0 {
            window[c]++
            if window[c] == need[c] {
                valid++
            }
        }

        // check if the left side of the window needs to shrink
        for right-left >= len(t) {
            // check here if a valid substring is found
            if valid == len(need) {
                return true
            }
            d := rune(s[left])
            left++
            // update the data inside the window
            if need[d] > 0 {
                if window[d] == need[d] {
                    valid--
                }
                window[d]--
            }
        }
    }
    // no valid substring found
    return false
}

javascript

var checkInclusion = function(t, s) {
    // determine if there is a permutation of t in s
    let need = new Map();
    let window = new Map();
    for (let c of t) {
        need.set(c, (need.get(c) || 0) + 1);
    }

    let left = 0, right = 0;
    let valid = 0;
    while (right < s.length) {
        let c = s.charAt(right);
        right++;
        // update the data inside the window
        if (need.has(c)) {
            window.set(c, (window.get(c) || 0) + 1);
            if (window.get(c) === need.get(c)) {
                valid++;
            }
        }

        // check if the left side of the window needs to shrink
        while (right - left >= t.length) {
            // check here if a valid substring is found
            if (valid === need.size) {
                return true;
            }
            let d = s.charAt(left);
            left++;
            // update the data inside the window
            if (need.has(d)) {
                if (window.get(d) === need.get(d)) {
                    valid--;
                }
                window.set(d, window.get(d) - 1);
            }
        }
    }
    // no valid substring found
    return false;
};

You can open the visual panel below and click the line while (right < s.length) multiple times to see how the fixed-length window slides:

Algorithm Visualization

The code for this problem is almost the same as the code for the minimum window substring. You only need to change a few things:

In this problem, you move left to shrink the window when the window size is greater than t.length(). Since we are looking for a permutation, the lengths must be the same.
When you find valid == need.size(), it means the window is a valid permutation, so return true right away.

How to move the window is the same as the minimum window substring problem.

Small Optimization

In this problem, the window [left, right) is always a fixed size, which is t.length(). Each time the window moves, only one character leaves the window. So you can change the inner while loop to an if statement, and it will work the same.

3. Find All Anagrams in a String

This is LeetCode Problem 438 "Find All Anagrams in a String", medium level:

438. Find All Anagrams in a String | LeetCode | 🟠

Given two strings s and p, return an array of all the start indices of p's anagrams in s. You may return the answer in any order.

An Anagram is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.

Example 1:

Input: s = "cbaebabacd", p = "abc"
Output: [0,6]
Explanation:
The substring with start index = 0 is "cba", which is an anagram of "abc".
The substring with start index = 6 is "bac", which is an anagram of "abc".

Example 2:

Input: s = "abab", p = "ab"
Output: [0,1,2]
Explanation:
The substring with start index = 0 is "ab", which is an anagram of "ab".
The substring with start index = 1 is "ba", which is an anagram of "ab".
The substring with start index = 2 is "ab", which is an anagram of "ab".

Constraints:

1 <= s.length, p.length <= 3 * 10⁴
s and p consist of lowercase English letters.

The problem is from LeetCode 438. Find All Anagrams in a String.

An anagram is just a permutation. The problem gives it a fancy name, but it is the same. You are given a string S and a string T. Find all the starting indexes of T's permutations in S.

Just copy the sliding window framework, answer the three key questions, and you can solve this problem:

java

class Solution {
    public List<Integer> findAnagrams(String s, String t) {
        Map<Character, Integer> need = new HashMap<>();
        Map<Character, Integer> window = new HashMap<>();
        for (char c : t.toCharArray()) {
            need.put(c, need.getOrDefault(c, 0) + 1);
        }

        int left = 0, right = 0;
        int valid = 0;
        // record the result
        List<Integer> res = new ArrayList<>();
        while (right < s.length()) {
            char c = s.charAt(right);
            right++;
            // update various data within the window
            if (need.containsKey(c)) {
                window.put(c, window.getOrDefault(c, 0) + 1);
                if (window.get(c).equals(need.get(c))) {
                    valid++;
                }
            }
            // check if the left side of the window needs to shrink
            while (right - left >= t.length()) {
                // when the window meets the condition, add the starting index to res
                if (valid == need.size()) {
                    res.add(left);
                }
                char d = s.charAt(left);
                left++;
                // update various data within the window
                if (need.containsKey(d)) {
                    if (window.get(d).equals(need.get(d))) {
                        valid--;
                    }
                    window.put(d, window.get(d) - 1);
                }
            }
        }
        return res;
    }
}

cpp

#include <vector>
#include <string>
#include <unordered_map>

using namespace std;

class Solution {
public:
    vector<int> findAnagrams(string s, string t) {
        unordered_map<char, int> need;
        unordered_map<char, int> window;
        for (char c : t) {
            need[c]++;
        }

        int left = 0, right = 0;
        int valid = 0;
        // record the result
        vector<int> res;
        while (right < s.size()) {
            char c = s[right];
            right++;
            // update various data within the window
            if (need.count(c)) {
                window[c]++;
                if (window[c] == need[c]) {
                    valid++;
                }
            }
            // check if the left side of the window needs to shrink
            while (right - left >= t.size()) {
                // when the window meets the condition, add the starting index to res
                if (valid == need.size()) {
                    res.push_back(left);
                }
                char d = s[left];
                left++;
                // update various data within the window
                if (need.count(d)) {
                    if (window[d] == need[d]) {
                        valid--;
                    }
                    window[d]--;
                }
            }
        }
        return res;
    }
};

python

class Solution:
    def findAnagrams(self, s: str, t: str) -> list[int]:
        need = {}
        window = {}
        for c in t:
            need[c] = need.get(c, 0) + 1

        left = 0
        right = 0
        valid = 0
        # record the result
        res = []
        while right < len(s):
            c = s[right]
            right += 1
            # update various data within the window
            if c in need:
                window[c] = window.get(c, 0) + 1
                if window[c] == need[c]:
                    valid += 1
            # check if the left side of the window needs to shrink
            while right - left >= len(t):
                # when the window meets the condition, add the starting index to res
                if valid == len(need):
                    res.append(left)
                d = s[left]
                left += 1
                # update various data within the window
                if d in need:
                    if window[d] == need[d]:
                        valid -= 1
                    window[d] -= 1
        return res

func findAnagrams(s string, t string) []int {
    need := make(map[rune]int)
    window := make(map[rune]int)
    for _, c := range t {
        need[c] = need[c] + 1
    }

    left, right, valid := 0, 0, 0
    // record the result
    res := []int{}
    for right < len(s) {
        c := rune(s[right])
        right++
        // update various data within the window
        if _, ok := need[c]; ok {
            window[c] = window[c] + 1
            if window[c] == need[c] {
                valid++
            }
        }
        // check if the left side of the window needs to shrink
        for right-left >= len(t) {
            // when the window meets the condition, add the starting index to res
            if valid == len(need) {
                res = append(res, left)
            }
            d := rune(s[left])
            left++
            // update various data within the window
            if _, ok := need[d]; ok {
                if window[d] == need[d] {
                    valid--
                }
                window[d] = window[d] - 1
            }
        }
    }
    return res
}

javascript

var findAnagrams = function(s, t) {
    let need = new Map();
    let window = new Map();
    for (let c of t) {
        need.set(c, (need.get(c) || 0) + 1);
    }

    let left = 0, right = 0;
    let valid = 0;
    // record the result
    let res = [];
    while (right < s.length) {
        let c = s[right];
        right++;
        // update various data within the window
        if (need.has(c)) {
            window.set(c, (window.get(c) || 0) + 1);
            if (window.get(c) === need.get(c)) {
                valid++;
            }
        }
        // check if the left side of the window needs to shrink
        while (right - left >= t.length) {
            // when the window meets the condition, add the starting index to res
            if (valid === need.size) {
                res.push(left);
            }
            let d = s[left];
            left++;
            // update various data within the window
            if (need.has(d)) {
                if (window.get(d) === need.get(d)) {
                    valid--;
                }
                window.set(d, window.get(d) - 1);
            }
        }
    }
    return res;
};

This is almost the same as the previous problem. When you find a valid anagram (permutation), just save the starting index in res.

You can open the visual panel below and click the line while (right < s.length) multiple times to see how the fixed-length window slides:

Algorithm Visualization

4. Longest Substring Without Repeating Characters

This is LeetCode Problem 3 "Longest Substring Without Repeating Characters", medium level:

3. Longest Substring Without Repeating Characters | LeetCode | 🟠

Given a string s, find the length of the longest substring without repeating characters.

Example 1:

Input: s = "abcabcbb"
Output: 3
Explanation: The answer is "abc", with the length of 3.

Example 2:

Input: s = "bbbbb"
Output: 1
Explanation: The answer is "b", with the length of 1.

Example 3:

Input: s = "pwwkew"
Output: 3
Explanation: The answer is "wke", with the length of 3.
Notice that the answer must be a substring, "pwke" is a subsequence and not a substring.

Constraints:

0 <= s.length <= 5 * 10⁴
s consists of English letters, digits, symbols and spaces.

The problem is from LeetCode 3. Longest Substring Without Repeating Characters.

This problem is a bit different. You cannot use the same template directly, but it is actually simpler. Just make a small change:

java

class Solution {
    public int lengthOfLongestSubstring(String s) {
        Map<Character, Integer> window = new HashMap<>();

        int left = 0, right = 0;
        // record the result
        int res = 0;
        while (right < s.length()) {
            char c = s.charAt(right);
            right++;
            // perform a series of updates within the window
            window.put(c, window.getOrDefault(c, 0) + 1);
            // determine whether the left side of the window needs to shrink
            while (window.get(c) > 1) {
                char d = s.charAt(left);
                left++;
                // perform a series of updates within the window
                window.put(d, window.get(d) - 1);
            }
            // update the result here
            res = Math.max(res, right - left);
        }
        return res;
    }
}

cpp

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        unordered_map<char, int> window;

        int left = 0, right = 0;
        // record the result
        int res = 0;
        while (right < s.size()) {
            char c = s[right];
            right++;
            // perform a series of updates within the window
            window[c]++;
            // determine whether the left side of the window needs to shrink
            while (window[c] > 1) {
                char d = s[left];
                left++;
                // perform a series of updates within the window
                window[d]--;
            }
            // update the result here
            res = max(res, right - left);
        }
        return res;
    }
};

python

class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        window = {}
        
        left = 0
        right = 0
        # record the result
        res = 0
        while right < len(s):
            c = s[right]
            right += 1
            # perform a series of updates within the window
            window[c] = window.get(c, 0) + 1
            # determine whether the left side of the window needs to shrink
            while window[c] > 1:
                d = s[left]
                left += 1
                # perform a series of updates within the window
                window[d] = window.get(d, 0) - 1
            # update the result here
            res = max(res, right - left)
        return res

func lengthOfLongestSubstring(s string) int {
    window := make(map[rune]int)

    left, right := 0, 0
    // record the result
    res := 0
    for right < len(s) {
        c := rune(s[right])
        right++
        // perform a series of updates within the window
        window[c] = window[c] + 1
        // determine whether the left side of the window needs to shrink
        for window[c] > 1 {
            d := rune(s[left])
            left++
            // perform a series of updates within the window
            window[d] = window[d] - 1
        }
        // update the result here
        if res < right-left {
            res = right - left
        }
    }
    return res
}

javascript

var lengthOfLongestSubstring = function(s) {
    let window = new Map();

    let left = 0, right = 0;
    // record the result
    let res = 0;
    while (right < s.length) {
        let c = s.charAt(right);
        right++;
        // perform a series of updates within the window
        window.set(c, (window.get(c) || 0) + 1);
        // determine whether the left side of the window needs to shrink
        while (window.get(c) > 1) {
            let d = s.charAt(left);
            left++;
            // perform a series of updates within the window
            window.set(d, window.get(d) - 1);
        }
        // update the result here
        res = Math.max(res, right - left);
    }
    return res;
};

You can open the visual panel below and click the line while (right < s.length) multiple times to see how the window updates the answer:

Algorithm Visualization

This problem is simpler. You do not need need and valid. You only need to update the character count in the window.

If window[c] is greater than 1, it means there are repeated characters in the window. Then you need to move left to shrink the window.

One thing to pay attention to is: when should you update the result res? We want the longest substring without repeating characters. At which moment does the window have no repeated characters?

This is different from before. You should update res after shrinking the window. The while loop for shrinking only runs when there are repeated characters. After shrinking, the window must have no repeated characters.

That is all for the sliding window algorithm template. I hope you can understand the logic, remember the template, and apply it. To review, when you face a problem about subarrays or substrings, if you can answer these three questions, you can use the sliding window algorithm:

When should you expand the window?
When should you shrink the window?
When should you update the answer?

In Sliding Window Exercise Collection, I list more classic problems using this way of thinking, to help you understand and remember the algorithm. After that, you will not be afraid of substring or subarray problems.

Related Problems

You can install my Chrome extension then open the link.

LeetCode	Difficulty
1004. Max Consecutive Ones III	🟠
1438. Longest Continuous Subarray With Absolute Diff Less Than or Equal to Limit	🟠
1658. Minimum Operations to Reduce X to Zero	🟠
209. Minimum Size Subarray Sum	🟠
219. Contains Duplicate II
220. Contains Duplicate III	🔴
340. Longest Substring with At Most K Distinct Characters🔒	🟠
395. Longest Substring with At Least K Repeating Characters	🟠
424. Longest Repeating Character Replacement	🟠
560. Subarray Sum Equals K	🟠
713. Subarray Product Less Than K	🟠
862. Shortest Subarray with Sum at Least K	🔴