Sliding Window Algorithm Code Template

labuladongOriginalAbout 7034 words

Note

Now all the plugins has supported English. I'm still improving the website...

This article will resolve

LeetCode	Difficulty
3. Longest Substring Without Repeating Characters	🟠
438. Find All Anagrams in a String	🟠
567. Permutation in String	🟠
76. Minimum Window Substring	🔴

前置知识

阅读本文前，你需要先学习：

For the use of fast and slow pointers and left and right pointers in the two-pointer technique, you can refer to the previous article Overview of Two-Pointer Techniques. This article focuses on solving one of the most challenging two-pointer techniques: the sliding window technique. A framework is summarized here, ensuring you can write the correct solution effortlessly.

Overview of the Sliding Window Framework

The sliding window algorithm technique is mainly used to solve subarray problems, such as finding the longest/shortest subarray that meets a specific condition.

If you use a brute-force solution, you would need to nest for loops to enumerate all subarrays, resulting in a time complexity of $O(N^2)$ :

for (int i = 0; i < nums.length; i++) {
    for (int j = i; j < nums.length; j++) {
        // nums[i, j] is a subarray
    }
}

The idea behind the sliding window algorithm technique is not difficult. It involves maintaining a window that slides continuously, and then updating the answer. The general logic of this algorithm is as follows:

int left = 0, right = 0;

while (right < nums.size()) {
    // expand the window
    window.addLast(nums[right]);
    right++;
    
    while (window needs shrink) {
        // shrink the window
        window.removeFirst(nums[left]);
        left++;
    }
}

The code written based on the sliding window algorithm framework has a time complexity of $O(N)$ , which is more efficient than the brute-force solution using nested for loops.

Why is it $O(N)$ ?

Some readers might ask, isn't your sliding window framework using a nested while loop as well? Why is the complexity $O(N)$ then?

In simple terms, the pointers left and right do not move backward (their values only increase and do not decrease), so each element in the string/array only enters the window once and is then removed once. No element enters and exits the window multiple times, so the time complexity of the algorithm is proportional to the length of the string/array.

In contrast, the brute-force solution with nested for loops allows the index j to move backward, causing some elements to enter and leave the window multiple times, resulting in a time complexity of $O(N^2)$ .

I have provided a detailed guide on how to theoretically estimate time and space complexity in A Practical Guide to Time and Space Complexity Analysis, so I won't go into it here.

Why can the sliding window enumerate subarrays in $O(N)$ time?

This question is inherently incorrect. The sliding window cannot enumerate all substrings. To enumerate all substrings, one must use the nested for loop.

However, for certain problems, it is unnecessary to enumerate all substrings to find the desired answer. The sliding window is an algorithm template for such scenarios, helping you prune the enumeration process and avoid redundant calculations.

Therefore, in The Essence of Algorithms, I categorize the sliding window algorithm under "how to enumerate intelligently."

What troubles many is not the algorithm's concept but the various detailed issues. For example, how to add new elements to the window, how to shrink the window, and at which stage of window movement to update the results. Even if you understand these details, the code can still easily contain bugs, and it can be frustrating not knowing how to find them.

So today, I will write a framework for the sliding window algorithm code. I've even included where to output debug information. When you encounter related problems in the future, just memorize the framework below and modify three places to ensure no bugs will arise.

Since most examples in this article are problems related to substrings, where a string essentially acts as an array, I'll set the input as a string. When solving problems, adapt according to the specific requirements of the problem:

java 🟢

// Pseudocode framework of sliding window algorithm
void slidingWindow(String s) {
    // Use an appropriate data structure to record the data in
    // the window, which can vary according to the specific
    // For example, if I want to record the
    // frequency of elements in the window, I would
    // If I want to record the sum of elements in the window, I could just use an int
    Object window = ...
    
    int left = 0, right = 0;
    while (right < s.length()) {
        // c is the character that will be added to the window
        char c = s[right];
        window.add(c)
        // Expand the window
        right++;
        // Perform a series of updates to the data within the window
        ...

        // *** Position of debug output ***
        // Note that in the final solution code, do not use print
        // Because IO operations are time-consuming and may cause timeouts
        printf("window: [%d, %d)\n", left, right);
        // ***********************

        // Determine whether the left side of the window needs to shrink
        while (left < right && window needs shrink) {
            // d is the character that will be removed from the window
            char d = s[left];
            window.remove(d)
            // Shrink the window
            left++;
            // Perform a series of updates to the data within the window
            ...
        }
    }
}

cpp 🤖

// Pseudocode framework of sliding window algorithm
void slidingWindow(string s) {
    // Use an appropriate data structure to record the
    // data in the window, varying with the specific
    // For instance, if I want to record the
    // frequency of elements in the window, I would
    // If I want to record the sum of elements in the window, I can simply use an int
    auto window = ...

    int left = 0, right = 0;
    while (right < s.size()) {
        // c is the character that will be entering the window
        char c = s[right];
        window.add(c);
        // Expand the window
        right++;

        // Perform a series of updates to the data within the window
        ...

        // *** position of debug output ***
        printf("window: [%d, %d)\n", left, right);
        // Note that printing should be avoided in the final solution code
        // Because IO operations are time-consuming and may cause timeouts

        // Determine whether the left side of the window needs to shrink
        while (window needs shrink) {
            // d is the character that will be removed from the window
            char d = s[left];
            window.remove(d);
            // Shrink the window
            left++;

            // Perform a series of updates to the data within the window
            ...
        }
    }
}

python 🤖

# Pseudocode framework for sliding window algorithm
def slidingWindow(s: str):
    # Use an appropriate data structure to record the data
    # in the window, which can vary depending on the
    # For example, if I want to record the
    # frequency of elements in the window, I would
    # If I want to record the sum of elements in the window, I could just use an int
    window = ...

    left, right = 0, 0
    while right < len(s):
        # c is the character that will be added to the window
        c = s[right]
        window.add(c)
        # Expand the window
        right += 1
        # Perform a series of updates on the data within the window
        ...

        # *** position for debug output ***
        # Note that you should not print in the final solution code
        # because IO operations are time-consuming and may cause timeouts
        # print(f"window: [{left}, {right})")
        # ***********************

        # Determine whether the left side of the window needs to be contracted
        while left < right and window needs shrink:
            # d is the character that will be removed from the window
            d = s[left]
            window.remove(d)
            # Shrink the window
            left += 1
            # Perform a series of updates on the data within the window
            ...

go 🤖

// Pseudocode framework for sliding window algorithm
func slidingWindow(s string) {
    // Use an appropriate data structure to record the data in
    // the window, which can vary according to the specific
    // For example, if I want to record the frequency of elements in the window, I use a map
    // If I want to record the sum of elements in the window, I can just use an int
    var window = ...

    left, right := 0, 0
    for right < len(s) {
        // c is the character to be moved into the window
        c := rune(s[right])
        window[c]++
        // Expand the window
        right++
        // Perform a series of updates to the data within the window
        ...

        // *** debug output location ***
        // Note that in the final solution code, do not print
        // Because IO operations are time-consuming and may cause timeouts
        fmt.Println("window: [",left,", ",right,")")
        // ***********************

        // Determine whether the left window needs to shrink
        for left < right && window needs shrink { //replace "window needs shrink" with actual condition
            // d is the character to be moved out of the window
            d := rune(s[left])
            window[d]--
            // Shrink the window
            left++
            // Perform a series of updates to the data within the window
            ...
        }
    }
}

javascript 🤖

// Pseudocode framework for sliding window algorithm
var slidingWindow = function(s) {
    // Use an appropriate data structure to record the data
    // in the window, which can vary according to the
    // For example, if I want to record the frequency of elements in the window, I use a map
    // If I want to record the sum of the elements in the window, I can just use an int
    var window = ...;

    var left = 0, right = 0;
    while (right < s.length) {
        // c is the character that will be moved into the window
        var c = s[right];
        window.add(c);
        // Expand the window
        right++;
        // Perform a series of updates on the data within the window
        ...

        // *** debug output position ***
        // Note that in the final solution code, do not print
        // Because IO operations are time-consuming and may cause timeouts
        console.log("window: [%d, %d)\n", left, right);
        // *********************

        // Determine whether the left side of the window needs to shrink
        while (window needs shrink) {
            // d is the character that will be moved out of the window
            var d = s[left];
            window.remove(d);
            // Shrink the window
            left++;
            // Perform a series of updates on the data within the window
            ...
        }
    }
};

In the framework, the two places marked with ... represent where you need to update the window data. Your task in specific problems is to fill in the code logic here. Moreover, the operations at these two ... places are for expanding and shrinking the window, respectively, and you will find that they are completely symmetric.

As a side note, some readers have commented on this framework, suggesting that hash tables are slow and should be replaced with arrays. Others prefer writing very concise code, claiming that my approach is too verbose and not fast enough. My view is that algorithms should primarily be judged by their time complexity. As long as you can ensure optimal time complexity, that's what matters. Regarding LeetCode's execution speed, it can be a bit unpredictable. As long as your solution isn't ridiculously slow, it's fine. There's no need to optimize at the compilation level and miss the forest for the trees...

Furthermore, the focus of my algorithm tutorials is on the algorithmic thinking. First, master the framework mindset, and then feel free to modify the code as you like. This ensures that you can write correct solutions no matter how you implement them.

Getting back on topic, let's apply this framework to four original LeetCode problems. I will explain the principles in detail for the first problem, and then you can solve the remaining three problems almost effortlessly.

1. Minimum Window Substring

Let's start with LeetCode problem #76, "Minimum Window Substring," which is classified as Hard:

76. Minimum Window Substring | LeetCode |

Given two strings s and t of lengths m and n respectively, return the minimum window substring of s such that every character in t (including duplicates) is included in the window. If there is no such substring, return the empty string "".

The testcases will be generated such that the answer is unique.

Example 1:

Input: s = "ADOBECODEBANC", t = "ABC"
Output: "BANC"
Explanation: The minimum window substring "BANC" includes 'A', 'B', and 'C' from string t.

Example 2:

Input: s = "a", t = "a"
Output: "a"
Explanation: The entire string s is the minimum window.

Example 3:

Input: s = "a", t = "aa"
Output: ""
Explanation: Both 'a's from t must be included in the window.
Since the largest window of s only has one 'a', return empty string.

Constraints:

m == s.length
n == t.length
1 <= m, n <= 10⁵
s and t consist of uppercase and lowercase English letters.

Follow up: Could you find an algorithm that runs in O(m + n) time?

The goal is to find a substring in S (source) that contains all the characters from T (target), and this substring must be the shortest among all possible substrings.

If we use a brute-force approach, the code would look something like this:

for (int i = 0; i < s.length(); i++)
    for (int j = i + 1; j < s.length(); j++)
        if s[i:j] 包含 t 的所有字母:
            更新答案

The idea is straightforward, but obviously, the complexity of this algorithm is definitely greater than O(N^2), which is not good.

The sliding window algorithm works like this:

We use two pointers, left and right, in the string S, initializing left = right = 0. We call the index interval [left, right) a "window."

Why use a "left-closed, right-open" interval

Theoretically, you can design intervals that are open at both ends or closed at both ends, but a left-closed, right-open interval is the most convenient to handle.

This is because when initialized as left = right = 0, the interval [0, 0) contains no elements. But as soon as you move right one step to the right (expanding), the interval [0, 1) includes one element, 0.

If you use an interval that is open at both ends, moving right one step to the right still leaves the interval (0, 1) empty. If you use an interval that is closed at both ends, the initial interval [0, 0] already includes one element. Both scenarios create unnecessary boundary handling issues.

We continuously increase the right pointer to expand the window [left, right) until the substring in the window meets the requirement (contains all characters in T).
At this point, we stop increasing right and start increasing the left pointer to shrink the window [left, right) until the substring no longer meets the requirement (does not contain all characters in T). Each time we increase left, we update the result.
Repeat steps 2 and 3 until right reaches the end of the string S.

This approach is not difficult. Step 2 is like finding a "feasible solution," and step 3 is optimizing this "feasible solution" to find the optimal solution, which is the shortest covering substring. The left and right pointers take turns moving forward, and the window size increases and decreases, resembling a caterpillar stretching and shrinking as it slides to the right. This is where the name "sliding window" comes from.

Let's visualize the process. needs and window act as counters, recording the frequency of characters in T and the corresponding characters in the "window," respectively.

Initial state:

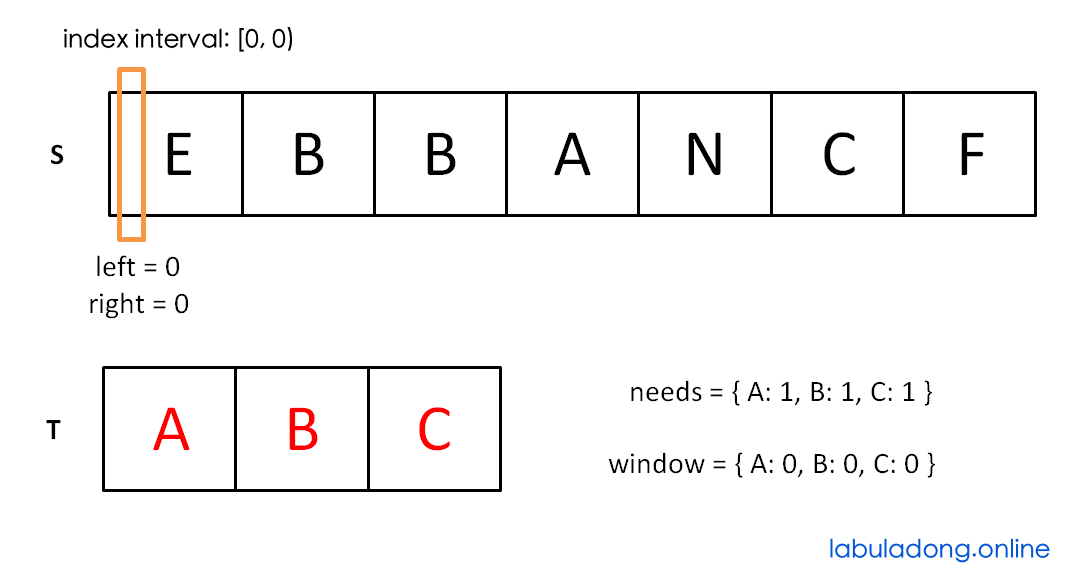
Increase right until the window [left, right) contains all characters from T:

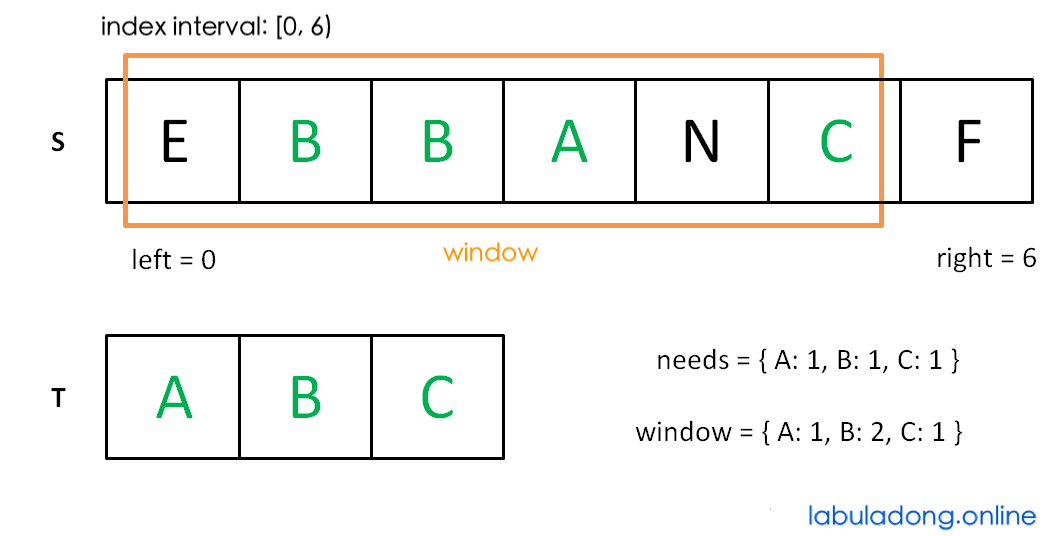
Now, start increasing left to shrink the window [left, right):

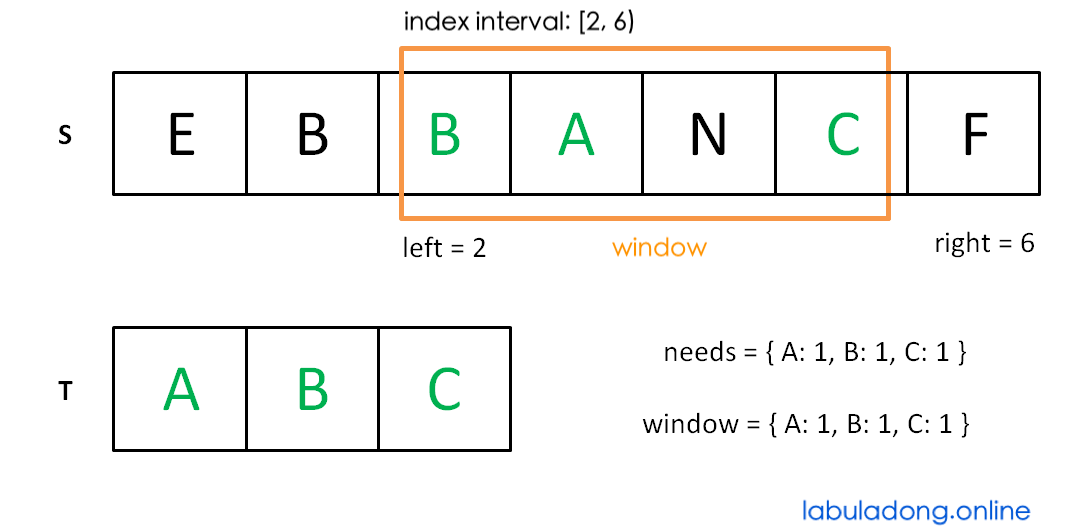
Continue until the string in the window no longer meets the requirements, and left stops moving:

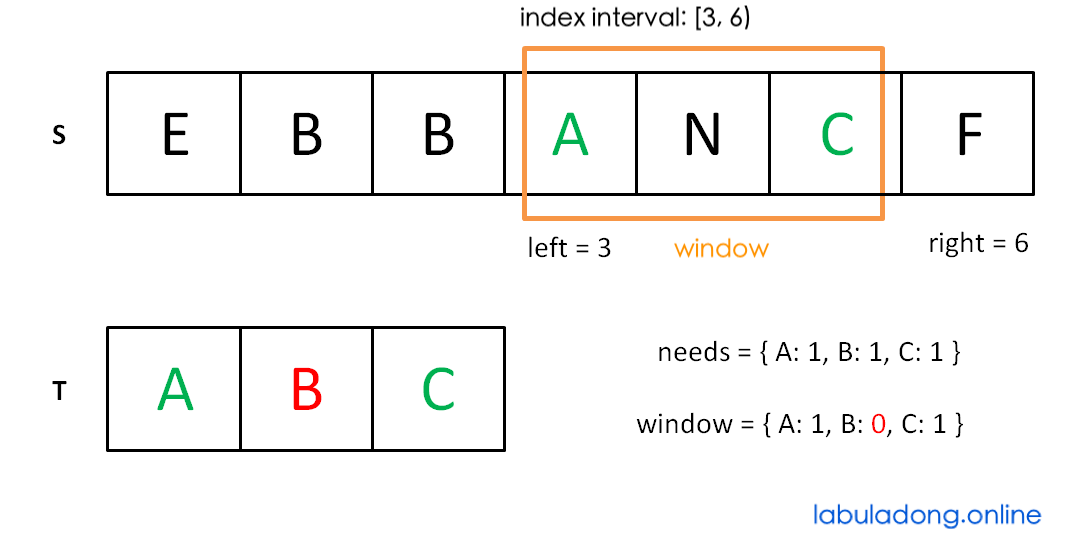
Repeat the above process: move right first, then left... until the right pointer reaches the end of string S, at which point the algorithm ends.

If you understand this process, congratulations! You've fully grasped the sliding window algorithm concept. Now let's see how to use this sliding window code framework:

First, initialize two hash tables, window and need, to record the characters in the window and the characters needed to complete the set:

// Record the frequency of characters in the window
HashMap<Character, Integer> window = new HashMap<>();
// Record the frequency of characters needed
HashMap<Character, Integer> need = new HashMap<>();
for (int i = 0; i < t.length(); i++) {
    char c = t.charAt(i);
    need.put(c, need.getOrDefault(c, 0) + 1);
}

Next, initialize the two ends of the window using the left and right variables. Don't forget, the interval [left, right) is left-closed and right-open, so initially, the window does not contain any elements:

int left = 0, right = 0;
int valid = 0;
while (right < s.length()) {
    // c is the character to be added into the window
    char c = s.charAt(right);
    // move the window to the right
    right++;
    // perform a series of updates to the data within the window
    ...
}

The valid variable represents the number of characters in the window that meet the need conditions. If valid is equal to need.size, it means the window satisfies the conditions and completely covers the string T.

Now, let's apply the template. You only need to think about the following questions:

When should we move right to expand the window? What data should be updated when a character is added to the window?
When should the window stop expanding and start moving left to shrink? What data should be updated when a character is removed from the window?
When should we update our final result: during window expansion or contraction?

If a character enters the window, the window counter should be increased; if a character is about to leave the window, the window counter should be decreased; when valid meets need, the window should be contracted; and the final result should be updated during window contraction.

Here is the complete code:

java 🟢

class Solution {
    public String minWindow(String s, String t) {
        Map<Character, Integer> need = new HashMap<>();
        Map<Character, Integer> window = new HashMap<>();
        for (char c : t.toCharArray()) {
            need.put(c, need.getOrDefault(c, 0) + 1);
        }

        int left = 0, right = 0;
        int valid = 0;
        // record the start index and length of the minimum coverage substring
        int start = 0, len = Integer.MAX_VALUE;
        while (right < s.length()) {
            // c is the character that will be added to the window
            char c = s.charAt(right);
            // expand the window
            right++;
            // perform a series of updates to the data inside the window
            if (need.containsKey(c)) {
                window.put(c, window.getOrDefault(c, 0) + 1);
                if (window.get(c).equals(need.get(c)))
                    valid++;
            }

            // determine whether the left side of the window needs to be contracted
            while (valid == need.size()) {
                // update the minimum coverage substring here
                if (right - left < len) {
                    start = left;
                    len = right - left;
                }
                // d is the character that will be removed from the window
                char d = s.charAt(left);
                // shrink the window
                left++;
                // perform a series of updates to the data inside the window
                if (need.containsKey(d)) {
                    if (window.get(d).equals(need.get(d)))
                        valid--;
                    window.put(d, window.get(d) - 1);
                }                    
            }
        }
        // return the minimum coverage substring
        return len == Integer.MAX_VALUE ? "" : s.substring(start, start + len);
    }
}

cpp 🤖

class Solution {
public:
    string minWindow(string s, string t) {
        unordered_map<char, int> need, window;
        for (char c : t) {
            need[c]++;
        }

        int left = 0, right = 0;
        // record the number of characters in window that meet the need condition
        int valid = 0;
        // record the start index and length of the minimum covering substring
        int start = 0, len = INT_MAX;
        while (right < s.size()) {
            // c is the character to be moved into the window
            char c = s[right];
            // expand the window
            right++;
            // perform a series of updates to the data within the window
            if (need.count(c)) {
                window[c]++;
                if (window[c] == need[c])
                    valid++;
            }

            // determine whether the left window needs to be shrinked
            while (valid == need.size()) {
                // update the minimum covering substring here
                if (right - left < len) {
                    start = left;
                    len = right - left;
                }
                // d is the character to be moved out of the window
                char d = s[left];
                // shrink the window
                left++;
                // perform a series of updates to the data within the window
                if (need.count(d)) {
                    if (window[d] == need[d])
                        valid--;
                    window[d]--;
                }
            }
        }
        // return the minimum covering substring
        return len == INT_MAX ? "" : s.substr(start, len);
    }
};

python 🤖

class Solution:
    def minWindow(self, s: str, t: str) -> str:
        need, window = {}, {}
        for c in t:
            need[c] = need.get(c, 0) + 1

        left = 0
        right = 0
        valid = 0
        # record the start index and length of the minimum covering substring
        start = 0
        length = float('inf')
        while right < len(s):
            # c is the character that will be added to the window
            c = s[right]
            # expand the window
            right += 1
            # perform a series of updates to the data within the window
            if c in need:
                window[c] = window.get(c, 0) + 1
                if window[c] == need[c]:
                    valid += 1

            # determine whether the left side of the window needs to be contracted
            while valid == len(need): 
                # update the minimum covering substring here
                if right - left < length:
                    start = left
                    length = right - left
                # d is the character that will be removed from the window
                d = s[left]
                # shrink the window
                left += 1
                # perform a series of updates to the data within the window
                if d in need:
                    if window[d] == need[d]:
                        valid -= 1
                    window[d] -= 1

        # return the minimum covering substring
        return "" if length == float('inf') else s[start: start + length]

go 🤖

func minWindow(s string, t string) string {
    need, window := make(map[byte]int), make(map[byte]int)
    for i := range t {
        need[t[i]]++
    }

    left, right := 0, 0
    valid := 0
    // record the start index and length of the minimum covering substring
    start, length := 0, math.MaxInt32
    for right < len(s) {
        // c is the character that will be added to the window
        c := s[right]
        // expand the window
        right++
        // perform a series of updates to the data inside the window
        if _, ok := need[c]; ok {
            window[c]++
            if window[c] == need[c] {
                valid++
            }
        }

        // determine whether the left side of the window needs to be contracted
        for valid == len(need) {
            // update the minimum covering substring here
            if right - left < length {
                start = left
                length = right - left
            }
            // d is the character that will be removed from the window
            d := s[left]
            // shrink the window
            left++
            // perform a series of updates to the data inside the window
            if _, ok := need[d]; ok {
                if window[d] == need[d] {
                    valid--
                }
                window[d]--
            }
        }
    }
    // return the minimum covering substring
    if length == math.MaxInt32 {
        return ""
    }
    return s[start : start+length]
}

javascript 🤖

var minWindow = function(s, t) {
    let need = {}, window = {};
    for (let c of t) {
        need[c] = (need[c] || 0) + 1;
    }

    let left = 0, right = 0;
    let valid = 0;
    // record the start index and length of the minimum covering substring
    let start = 0, len = Infinity;
    while (right < s.length) {
        // c is the character to be moved into the window
        let c = s[right];
        // expand the window
        right++;
        // perform a series of updates to the data inside the window
        if (need[c]) {
            window[c] = (window[c] || 0) + 1;
            if (window[c] === need[c]) {
                valid++;
            }
        }

        // determine whether the left side of the window needs to shrink
        while (valid === Object.keys(need).length) {
            // update the minimum covering substring here
            if (right - left < len) {
                start = left;
                len = right - left;
            }
            // d is the character to be moved out of the window
            let d = s[left];
            // shrink the window
            left++;
            // perform a series of updates to the data inside the window
            if (need[d]) {
                if (window[d] === need[d]) {
                    valid--;
                }
                window[d]--;
            }
        }
    }
    // return the minimum covering substring
    return len === Infinity ? "" : s.substring(start, start + len);
};

Attention for Java Users

When comparing Java wrapper classes, exercise caution. Types like Integer and String should use the equals method to check for equality, instead of the == operator, which can lead to errors. Therefore, when updating data while narrowing the window, do not write window.get(d) == need.get(d); instead, use window.get(d).equals(need.get(d)). The same principle applies to the code in subsequent problems.

In the above code, when we find that the count of a character in the window meets the need, we should update valid, indicating that a character requirement has been satisfied. You will also notice that the two operations to update the data within the window are completely symmetrical.

When valid == need.size(), it means all characters in T have been covered, and we have a feasible covering substring. Now, the window should be contracted to find the "minimum covering substring."

When moving left to shrink the window, the characters within the window are part of a feasible solution. Therefore, updating the minimum covering substring should occur during this contraction phase to find the shortest final result among feasible solutions.

By now, you should fully understand this framework. The sliding window algorithm is not difficult, but the details can be quite bothersome. In the future, when faced with sliding window algorithms, follow this framework to write your code; it will ensure no bugs and save you trouble.

Let's apply this framework to quickly solve a few problems. You'll be able to discern the approach almost instantly.

2. String Permutations

This is LeetCode problem #567, "Permutation in String," with a medium difficulty level:

567. Permutation in String | LeetCode |

Given two strings s1 and s2, return true if s2 contains a permutation of s1, or false otherwise.

In other words, return true if one of s1's permutations is the substring of s2.

Example 1:

Input: s1 = "ab", s2 = "eidbaooo"
Output: true
Explanation: s2 contains one permutation of s1 ("ba").

Example 2:

Input: s1 = "ab", s2 = "eidboaoo"
Output: false

Constraints:

1 <= s1.length, s2.length <= 10⁴
s1 and s2 consist of lowercase English letters.

Note that the input s1 can contain duplicate characters, which makes this problem quite challenging.

This type of problem is a classic example of the sliding window algorithm. Essentially, you are given a string S and a string T. The question is whether there exists a substring in S that contains all characters of T and no other characters?

First, start by copying and pasting the previous algorithm framework code. Then, clarify the questions raised earlier, and you can write the solution to this problem:

java 🟢

class Solution {
    // determine if there is a permutation of t in s
    public boolean checkInclusion(String t, String s) {
        Map<Character, Integer> need = new HashMap<>();
        Map<Character, Integer> window = new HashMap<>();
        for (char c : t.toCharArray()) {
            need.put(c, need.getOrDefault(c, 0) + 1);
        }

        int left = 0, right = 0;
        int valid = 0;
        while (right < s.length()) {
            char c = s.charAt(right);
            right++;
            // perform a series of updates to the data within the window
            if (need.containsKey(c)) {
                window.put(c, window.getOrDefault(c, 0) + 1);
                if (window.get(c).intValue() == need.get(c).intValue())
                    valid++;
            }

            // determine if the left side of the window needs to shrink
            while (right - left >= t.length()) {
                // determine if a valid substring is found here
                if (valid == need.size())
                    return true;
                char d = s.charAt(left);
                left++;
                // perform a series of updates to the data within the window
                if (need.containsKey(d)) {
                    if (window.get(d).intValue() == need.get(d).intValue())
                        valid--;
                    window.put(d, window.get(d) - 1);
                }
            }
        }
        // no substring meeting the conditions was found
        return false;
    }
}

cpp 🤖

class Solution {
public:
    // determine if there is a permutation of t in s
    bool checkInclusion(string t, string s) {
        unordered_map<char, int> need, window;
        for (char c : t) {
            need[c]++;
        }

        int left = 0, right = 0;
        int valid = 0;
        while (right < s.size()) {
            char c = s[right];
            right++;
            // perform a series of updates to the data within the window
            if (need.count(c)) {
                window[c]++;
                if (window[c] == need[c])
                    valid++;
            }

            // determine if the left side of the window should shrink
            while (right - left >= t.size()) {
                // here, determine if a valid substring is found
                if (valid == need.size())
                    return true;
                char d = s[left];
                left++;
                // perform a series of updates to the data within the window
                if (need.count(d)) {
                    if (window[d] == need[d])
                        valid--;
                    window[d]--;
                }
            }
        }
        // no substring meeting the criteria was found
        return false;
    }
};

python 🤖

class Solution:
    # determine if there is a permutation of t in s
    def checkInclusion(self, t: str, s: str) -> bool:
        need, window = collections.defaultdict(int), collections.defaultdict(int)
        for c in t: 
            need[c] += 1

        left, right, valid = 0, 0, 0 
        while right < len(s):
            c = s[right]
            right += 1
            # perform a series of updates within the window
            if c in need:
                window[c] += 1
                if window[c] == need[c]:
                    valid += 1

            # determine if the left window needs to shrink
            while (right - left >= len(t)):
                # here determine if a valid substring is found
                if valid == len(need):
                    return True
                d = s[left]
                left += 1
                # perform a series of updates within the window
                if d in need:
                    if window[d] == need[d]:
                        valid -= 1
                    window[d] -= 1

        # no valid substring found
        return False

go 🤖

// Determine if there is a permutation of t in s
func checkInclusion(t string, s string) bool {
	need := make(map[rune]int)
	window := make(map[rune]int)

    for _, c := range t {
        need[c]++
    }

    left, right := 0, 0
    valid := 0
    for right < len(s) {
        c := rune(s[right])
        right++
        // Perform a series of updates within the window
        if _, ok := need[c]; ok {
            window[c]++
            if window[c] == need[c] {
                valid++
            }
        }

        // Determine if the left window needs to shrink
        for right - left >= len(t) {
            // Here, determine if a valid substring has been found
            if valid == len(need) {
                return true
            }
            d := rune(s[left])
            left++
            // Perform a series of updates within the window
            if _, ok := need[d]; ok {
                if window[d] == need[d] {
                    valid--
                }
                window[d]--
            }
        }
    }

    // No substring meeting the conditions was found
    return false
}

javascript 🤖

var checkInclusion = function(t, s){
    var need = new Map();
    var window = new Map();
    for (var c of t) {
        need.set(c, (need.get(c) || 0) + 1);
    }

    var left = 0, right = 0;
    var valid = 0;
    while (right < s.length) {
        var c = s[right];
        right++;
        // perform a series of updates within the window
        if (need.has(c)) {
            window.set(c, (window.get(c) || 0) + 1);
            if (window.get(c) === need.get(c))
                valid++;
        }

        // determine whether the left side of the window needs to shrink
        while (right - left >= t.length) {
            // here determine if a valid substring is found
            if (valid === need.size)
                return true;
            var d = s[left];
            left++;
            // perform a series of updates within the window
            if (need.has(d)) {
                if (window.get(d) === need.get(d))
                    valid--;
                window.set(d, window.get(d) - 1);
            }
        }
    }
    // no substring found that meets the criteria
    return false;
};

The solution code for this problem is basically identical to that of the "Minimum Window Substring," with only a few changes:

In this problem, the left pointer is moved to shrink the window when the window size exceeds t.length(), because for permutations, the lengths should obviously be the same.
When valid == need.size(), it indicates that the window contains a valid permutation, so you should immediately return true.

As for how to handle the expansion and contraction of the window, it is exactly the same as in the "Minimum Window Substring."

Minor Optimization

In this problem, [left, right) actually maintains a fixed-length window, with the window length being t.length(). Since a fixed-length window only slides forward by removing one character at a time, you can change the inner while loop to an if statement, and the effect will be the same.

III. Finding All Anagrams in a String

This is LeetCode problem #438, "Find All Anagrams in a String," with a medium difficulty level:

438. Find All Anagrams in a String | LeetCode |

Given two strings s and p, return an array of all the start indices of p's anagrams in s. You may return the answer in any order.

An Anagram is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.

Example 1:

Input: s = "cbaebabacd", p = "abc"
Output: [0,6]
Explanation:
The substring with start index = 0 is "cba", which is an anagram of "abc".
The substring with start index = 6 is "bac", which is an anagram of "abc".

Example 2:

Input: s = "abab", p = "ab"
Output: [0,1,2]
Explanation:
The substring with start index = 0 is "ab", which is an anagram of "ab".
The substring with start index = 1 is "ba", which is an anagram of "ab".
The substring with start index = 2 is "ab", which is an anagram of "ab".

Constraints:

1 <= s.length, p.length <= 3 * 10⁴
s and p consist of lowercase English letters.

Oh, this so-called letter anagram is just a permutation, right? Can a fancy term really fool people? In essence, you are given a string S and a string T. Your task is to find all permutations of T within S and return their starting indices.

Simply recall the framework discussed earlier, clarify the four key points, and you can solve this problem in no time:

java 🟢

class Solution {
    public List<Integer> findAnagrams(String s, String t) {
        Map<Character, Integer> need = new HashMap<>();
        Map<Character, Integer> window = new HashMap<>();
        for (char c : t.toCharArray()) {
            need.put(c, need.getOrDefault(c, 0) + 1);
        }

        int left = 0, right = 0;
        int valid = 0;
        // record the result
        List<Integer> res = new ArrayList<>();
        while (right < s.length()) {
            char c = s.charAt(right);
            right++;
            // perform a series of updates to the data within the window
            if (need.containsKey(c)) {
                window.put(c, window.getOrDefault(c, 0) + 1);
                if (window.get(c).equals(need.get(c))) {
                    valid++;
                }
            }
            // determine whether the left side of the window needs to shrink
            while (right - left >= t.length()) {
                // when the window meets the condition, add the starting index to res
                if (valid == need.size())
                    res.add(left);
                char d = s.charAt(left);
                left++;
                // perform a series of updates to the data within the window
                if (need.containsKey(d)) {
                    if (window.get(d).equals(need.get(d))) {
                        valid--;
                    }
                    window.put(d, window.get(d) - 1);
                }
            }
        }
        return res;
    }
}

cpp 🤖

class Solution {
public:
    vector<int> findAnagrams(string s, string t) {
        unordered_map<char, int> need, window;
        for (char c : t) {
            need[c]++;
        }

        int left = 0, right = 0;
        int valid = 0;
        // record the result
        vector<int> res;
        while (right < s.size()) {
            char c = s[right];
            right++;
            // perform a series of updates to the data within the window
            if (need.count(c)) {
                window[c]++;
                if (window[c] == need[c]) {
                    valid++;
                }
            }
            // determine whether the left window needs to shrink
            while (right - left >= t.size()) {
                // when the window meets the condition, add the starting index to res
                if (valid == need.size())
                    res.push_back(left);
                char d = s[left];
                left++;
                // perform a series of updates to the data within the window
                if (need.count(d)) {
                    if (window[d] == need[d]) {
                        valid--;
                    }
                    window[d]--;
                }
            }
        }
        return res;
    }
};

python 🤖

class Solution:
    def findAnagrams(self, s: str, t: str) -> List[int]:
        need = {}
        window = {}
        for c in t:
            need[c] = need.get(c, 0) + 1

        left = 0
        right = 0
        valid = 0
        # record the result
        res = []
        while right < len(s):
            c = s[right]
            right += 1
            # perform a series of updates to the data within the window
            if c in need:
                window[c] = window.get(c, 0) + 1
                if window[c] == need[c]:
                    valid += 1
            # determine whether the left side of the window should shrink
            while right - left >= len(t):
                # when the window meets the condition, add the starting index to res
                if valid == len(need):
                    res.append(left)
                d = s[left]
                left += 1
                # perform a series of updates to the data within the window
                if d in need:
                    if window[d] == need[d]:
                        valid -= 1
                    window[d] -= 1

        return res

go 🤖

func findAnagrams(s string, t string) []int {
    need, window := make(map[rune]int), make(map[rune]int)
    for _, c := range t {
        need[c]++
    }

    left, right := 0, 0
    valid := 0
    // record the result
    var res []int
    for right < len(s) {
        c := rune(s[right])
        right++
        // perform a series of updates within the window
        if _, ok := need[c]; ok {
            window[c]++
            if window[c] == need[c] {
                valid++
            }
        }
        // determine whether the left window needs to shrink
        for right - left >= len(t) {
            // when the window meets the condition, add the starting index to res
            if valid == len(need) {
                res = append(res, left)
            }
            d := rune(s[left])
            left++
            // perform a series of updates within the window
            if _, ok := need[d]; ok {
                if window[d] == need[d] {
                    valid--
                }
                window[d]--
            }
        }
    }
    return res
}

javascript 🤖

var findAnagrams = function(s, t) {
    let need = {};
    let window = {};
    for (let c of t) {
        need[c] = (need[c] || 0) + 1;
    }

    let left = 0, right = 0;
    let valid = 0;
    // record the result
    let res = [];
    while (right < s.length) {
        let c = s[right];
        right++;
        // perform a series of updates to the data within the window
        if (need[c] !== undefined) {
            window[c] = (window[c] || 0) + 1;
            if (window[c] === need[c]) {
                valid++;
            }
        }
        // determine whether the left side of the window needs to shrink
        while (right - left >= t.length) {
            // when the window meets the condition, add the starting index to res
            if (valid === Object.keys(need).length)
                res.push(left);
                let d = s[left];
                left++;
            // perform a series of updates to the data within the window
            if (need[d] !== undefined) {
                if (window[d] === need[d]) {
                    valid--;
                }
                window[d] = window[d] - 1;
            }
        }
    }
    return res;
};

Similar to finding permutations of a string, once you find a valid anagram (permutation), simply add the starting index to res.

4. Longest Substring Without Repeating Characters

This is LeetCode Problem 3 "Longest Substring Without Repeating Characters," with a medium difficulty level:

3. Longest Substring Without Repeating Characters | LeetCode |

Given a string s, find the length of the longest substring without repeating characters.

Example 1:

Input: s = "abcabcbb"
Output: 3
Explanation: The answer is "abc", with the length of 3.

Example 2:

Input: s = "bbbbb"
Output: 1
Explanation: The answer is "b", with the length of 1.

Example 3:

Input: s = "pwwkew"
Output: 3
Explanation: The answer is "wke", with the length of 3.
Notice that the answer must be a substring, "pwke" is a subsequence and not a substring.

Constraints:

0 <= s.length <= 5 * 10⁴
s consists of English letters, digits, symbols and spaces.

This problem introduces a bit of novelty; it's not just a framework that gives you the answer. However, it's actually simpler; you just need to slightly modify the framework:

java 🟢

class Solution {
    public int lengthOfLongestSubstring(String s) {
        Map<Character, Integer> window = new HashMap<>();
        int left = 0, right = 0;
        // record the result
        int res = 0;
        while (right < s.length()) {
            char c = s.charAt(right);
            right++;
            // perform a series of updates to the data within the window
            window.put(c, window.getOrDefault(c, 0) + 1);
            // determine whether the left window needs to shrink
            while (window.get(c) > 1) {
                char d = s.charAt(left);
                left++;
                // perform a series of updates to the data within the window
                window.put(d, window.get(d) - 1);
            }
            // update the answer here
            res = Math.max(res, right - left);
        }
        return res;
    }
}

cpp 🤖

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        unordered_map<char, int> window;
        int left = 0, right = 0;
        // record the result
        int res = 0;
        while (right < s.size()) {
            char c = s[right];
            right++;
            // perform a series of updates to the data within the window
            window[c]++;
            // determine whether the left window needs to shrink
            while (window[c] > 1) {
                char d = s[left];
                left++;
                // perform a series of updates to the data within the window
                window[d]--;
            }
            // update the answer here
            res = max(res, right - left);
        }
        return res;
    }
};

python 🤖

class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        window = {}
        left, right = 0, 0
        # record the result
        res = 0
        while right < len(s):
            c = s[right]
            right += 1
            # perform a series of updates to the data within the window
            window[c] = window.get(c, 0) + 1
            # determine whether the left window needs to shrink
            while window.get(c) > 1:
                d = s[left]
                left += 1
                # perform a series of updates to the data within the window
                window[d] -= 1
            # update the answer here
            res = max(res, right - left)
        return res

go 🤖

func lengthOfLongestSubstring(s string) int {
    window := make(map[rune]int)
    left := 0
    right := 0
    // record the result
    res := 0

    for right < len(s) {
        c := rune(s[right])
        right++

        // perform a series of updates to the data within the window
        window[c] = window[c] + 1

        // determine whether the left window needs to shrink
        for window[c] > 1 {
            d := rune(s[left])
            left++

            // perform a series of updates to the data within the window
            window[d] = window[d] - 1
        }

        // update the answer here
        if res < (right - left) {
            res = right - left
        }
    }

    return res
}

javascript 🤖

var lengthOfLongestSubstring = function(s) {
    var window = {};
    var left = 0, right = 0;
    // record the result
    var res = 0;
    while (right < s.length) {
        var c = s.charAt(right);
        right++;
        // update the data within the window
        window[c] = (window[c] || 0) + 1;
        // determine whether the left window needs to shrink
        while (window[c] > 1) {
            var d = s.charAt(left);
            left++;
            // update the data within the window
            window[d] = window[d] - 1;
        }
        // update the answer here
        res = Math.max(res, right - left);
    }
    return res;
};

This simplifies the process, as there is no need for need and valid, and updating the data within the window only requires a simple update to the counter window.

When the value of window[c] is greater than 1, it indicates there are duplicate characters in the window, which is not desirable, and the left should be moved to shrink the window.

The only thing to be mindful of is when to update the result res. We are looking for the longest substring without repeating characters, and at what stage can we ensure the string in the window contains no duplicates?

This is different from before; you should update res after shrinking the window, because the condition for the while loop to shrink is that there are duplicate elements. In other words, once shrinking is complete, the window is guaranteed to have no duplicates.

That's all for the sliding window algorithm template. I hope you understand the concept, remember the algorithm template, and apply it effectively. To recap, when you encounter problems related to subarrays or substrings, if you can answer the following questions, you can apply the sliding window algorithm:

When should you expand the window?
When should you shrink the window?
When should you update the answer?

In Classic Sliding Window Problems, I have listed more classic problems using this thought process to strengthen your understanding and memory of the algorithm, so you'll never fear substring or subarray problems again.

Related Problems

You can install my Chrome extension then open the link.

LeetCode	Difficulty
1004. Max Consecutive Ones III	🟠
1438. Longest Continuous Subarray With Absolute Diff Less Than or Equal to Limit	🟠
1658. Minimum Operations to Reduce X to Zero	🟠
209. Minimum Size Subarray Sum	🟠
219. Contains Duplicate II	🟢
220. Contains Duplicate III	🔴
340. Longest Substring with At Most K Distinct Characters🔒	🟠
395. Longest Substring with At Least K Repeating Characters	🟠
424. Longest Repeating Character Replacement	🟠
560. Subarray Sum Equals K	🟠
713. Subarray Product Less Than K	🟠
862. Shortest Subarray with Sum at Least K	🔴

Sliding Window Algorithm Code Template

3. 无重复字符的最长子串 https://leetcode.cn/problems/longest-substring-without-repeating-characters

3. Longest Substring Without Repeating Characters https://leetcode.com/problems/longest-substring-without-repeating-characters

438. 找到字符串中所有字母异位词 https://leetcode.cn/problems/find-all-anagrams-in-a-string

438. Find All Anagrams in a String https://leetcode.com/problems/find-all-anagrams-in-a-string

567. 字符串的排列 https://leetcode.cn/problems/permutation-in-string

567. Permutation in String https://leetcode.com/problems/permutation-in-string

76. 最小覆盖子串 https://leetcode.cn/problems/minimum-window-substring

76. Minimum Window Substring https://leetcode.com/problems/minimum-window-substring

Overview of the Sliding Window Framework

1. Minimum Window Substring

2. String Permutations

III. Finding All Anagrams in a String

4. Longest Substring Without Repeating Characters