Backtracking Algorithm to Solve All Permutation/Combination/Subset Problems
This article will resolve
| LeetCode | Difficulty |
|---|---|
| 216. Combination Sum III | 🟠 |
| 39. Combination Sum | 🟠 |
| 40. Combination Sum II | 🟠 |
| 46. Permutations | 🟠 |
| 47. Permutations II | 🟠 |
| 77. Combinations | 🟠 |
| 78. Subsets | 🟠 |
| 90. Subsets II | 🟠 |
Prerequisite Knowledge
Before reading this article, you should first learn:
Although problems about permutations, combinations, and subsets are taught in high school, writing algorithms to solve them requires strong computational thinking. This article explains the core ideas for programming solutions to these problems. Once you understand these concepts, you will be able to solve any variations that come up in the future.
Whether it's a permutation, combination, or subset problem, the task is essentially to select several elements from the sequence nums according to certain rules. There are several main variations:
Type 1: Elements are unique and cannot be reused. That is, all elements in nums are unique, and each element can be used at most once. This is the most basic form.
For example, in the combination problem, if the input is nums = [2,3,6,7], the combination that sums to 7 should only be [7].
Type 2: Elements can repeat in nums, but each can be used at most once.
For example, in the combination problem, if the input is nums = [2,5,2,1,2], the combinations that sum to 7 should be [2,2,2,1] and [5,2].
Type 3: Elements are unique and can be reused. That is, all elements in nums are unique, and each element can be used multiple times.
For example, in the combination problem, if the input is nums = [2,3,6,7], the combinations that sum to 7 should be [2,2,3] and [7].
Of course, there is a possible fourth type: elements can repeat in nums and can also be reused. However, if elements can be reused, there is no need for duplicates, because after removing duplicates, this becomes the same as Type 3. So this situation does not need to be considered.
The examples above use the combination problem, but permutation, combination, and subset problems can all have these three basic forms, so there are a total of 9 variations.
Additionally, the problem can include various constraints, such as finding a combination of elements that sum to a target with exactly k elements. This leads to many variations, which is why permutation and combination questions are frequently tested in interviews and exams.
Regardless of how the form changes, the essence is to enumerate all solutions, which naturally form a tree structure. By effectively using the backtracking algorithm framework and slightly modifying the code framework, you can tackle these problems comprehensively.
Specifically, you need to first read and understand the earlier article Core Techniques of Backtracking Algorithms. Then, by remembering the backtracking trees for the subset and permutation problems, you can solve all permutation, combination, and subset-related problems:
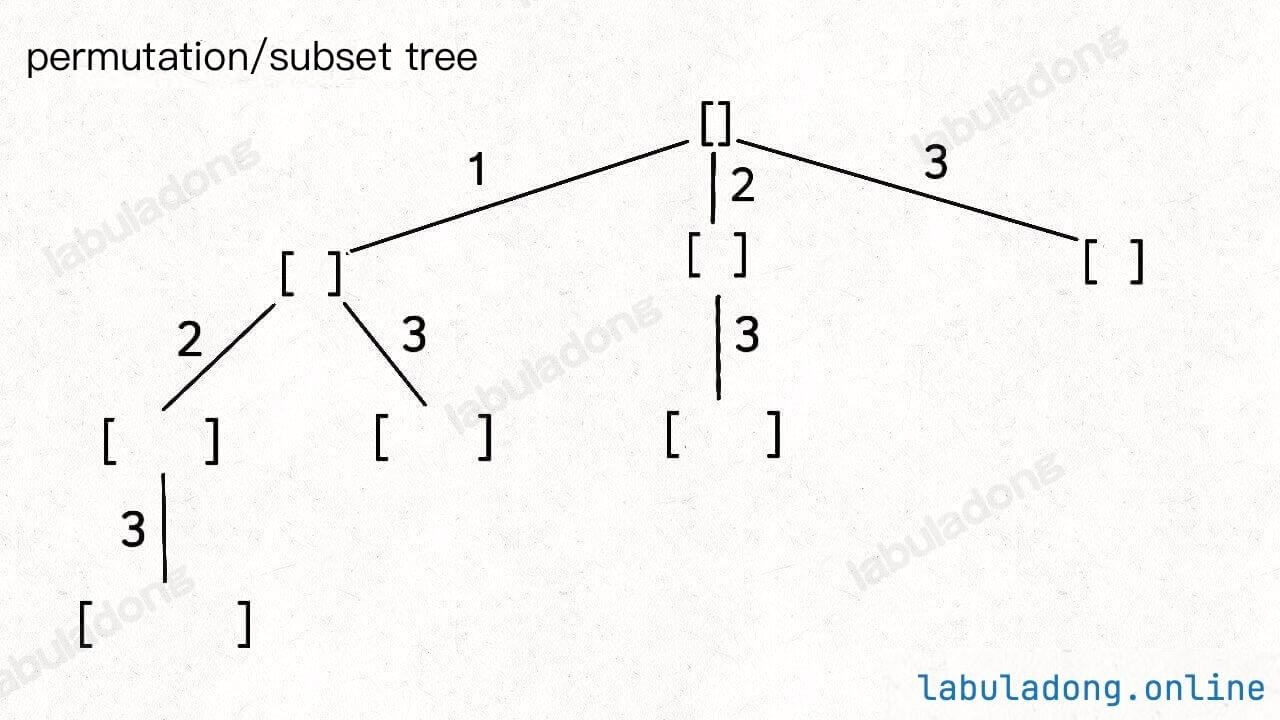
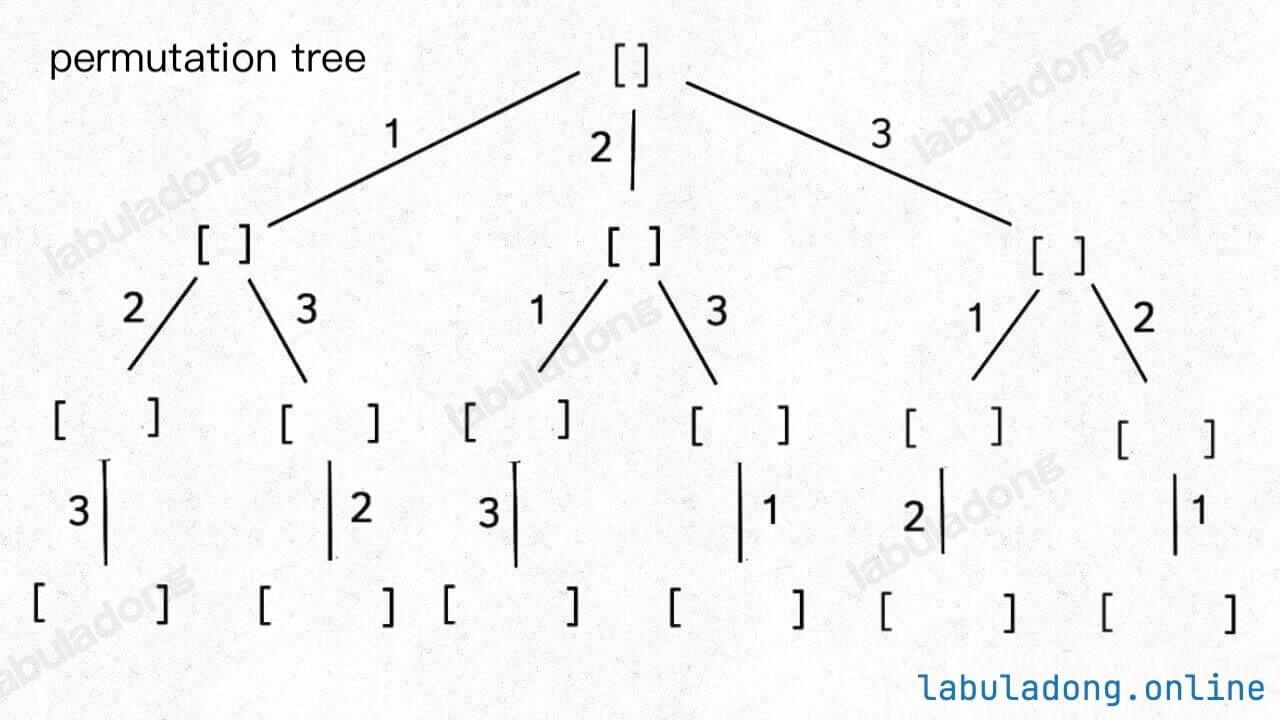
Why can you solve all related problems by remembering these two tree structures?
Firstly, combination problems and subset problems are actually equivalent, as will be explained later. As for the three variations mentioned earlier, they are merely modifications of these two trees, either by pruning or adding branches.
Next, we will enumerate all 9 forms of permutation/combination/subset problems and learn how to use the backtracking algorithm to handle them effectively.
Tip
Additionally, some readers might have encountered permutation/subset/combination solutions that differ from the ones introduced here. This is because there are two perspectives in backtracking algorithm enumeration. I will explain these perspectives in detail later in Ball and Box Model: Two Perspectives of Backtracking Algorithm Enumeration. For now, it is best to follow my approach.