Backtracking Algorithm to Solve All Permutation/Combination/Subset Problems
This article will resolve
| LeetCode | Difficulty |
|---|---|
| 216. Combination Sum III | 🟠 |
| 39. Combination Sum | 🟠 |
| 40. Combination Sum II | 🟠 |
| 46. Permutations | 🟠 |
| 47. Permutations II | 🟠 |
| 77. Combinations | 🟠 |
| 78. Subsets | 🟠 |
| 90. Subsets II | 🟠 |
Prerequisites
Before reading this article, you should first learn:
Although permutation, combination, and subset problems are learned in high school, writing algorithms to solve them can be quite challenging and requires good computational thinking. This article will discuss the core ideas for programming solutions to these problems, so you can handle any variations with ease, adapting to changes effortlessly.
Whether it's permutation, combination, or subset problems, simply put, you are asked to select several elements from a sequence nums according to given rules. There are mainly three variations:
Form 1: Elements are unique and non-reusable, meaning each element in nums is unique and can be used at most once. This is the most basic form.
For example, in combination, if the input nums = [2,3,6,7], the combinations that sum to 7 should only be [7].
Form 2: Elements can be repeated but are non-reusable, meaning elements in nums can be duplicated, but each element can still be used at most once.
For example, in combination, if the input nums = [2,5,2,1,2], the combinations that sum to 7 should be two: [2,2,2,1] and [5,2].
Form 3: Elements are unique and reusable, meaning each element in nums is unique and can be used multiple times.
For example, in combination, if the input nums = [2,3,6,7], the combinations that sum to 7 should be two: [2,2,3] and [7].
Of course, there could be a fourth form where elements can be repeated and reusable. But if elements are reusable, why have duplicates? Removing duplicates would make it equivalent to Form 3, so this case doesn't need separate consideration.
The examples above use combination problems, but permutation, combination, and subset problems can all have these three basic forms, resulting in a total of 9 variations.
Additionally, the problem can include various constraints, such as finding a combination of elements that sum to a target with exactly k elements. This leads to many variations, which is why permutation and combination questions are frequently tested in interviews and exams.
Regardless of how the form changes, the essence is to enumerate all solutions, which naturally form a tree structure. By effectively using the backtracking algorithm framework and slightly modifying the code framework, you can tackle these problems comprehensively.
Specifically, you need to first read and understand the earlier article Core Techniques of Backtracking Algorithms. Then, by remembering the backtracking trees for the subset and permutation problems, you can solve all permutation, combination, and subset-related problems:
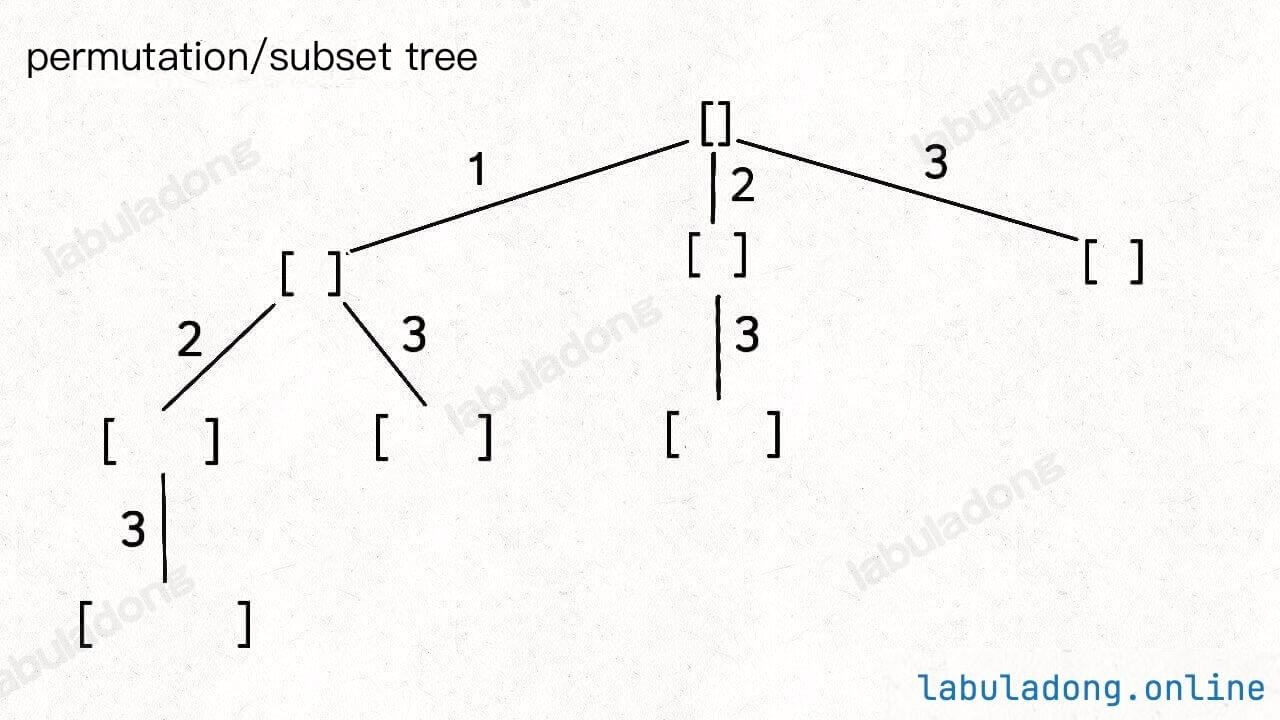
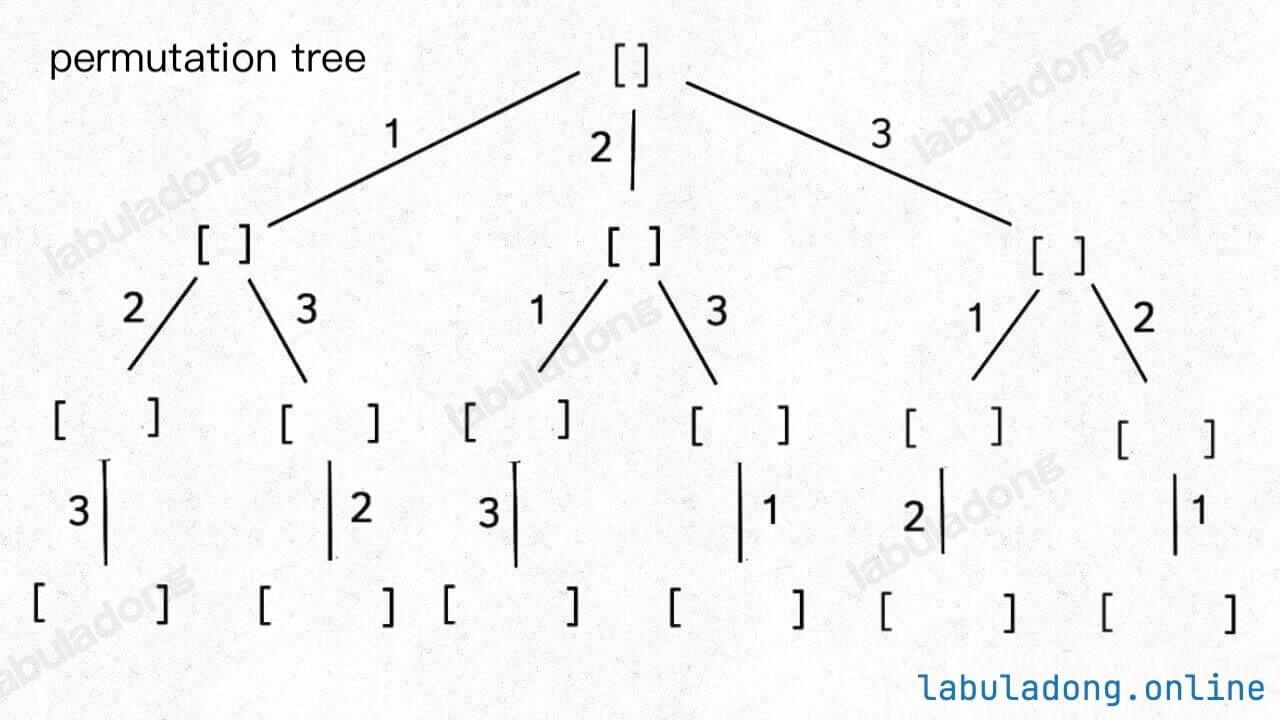
Why can you solve all related problems by remembering these two tree structures?
Firstly, combination problems and subset problems are actually equivalent, as will be explained later. As for the three variations mentioned earlier, they are merely modifications of these two trees, either by pruning or adding branches.
Next, we will enumerate all 9 forms of permutation/combination/subset problems and learn how to use the backtracking algorithm to handle them effectively.
Tip
Additionally, some readers might have encountered permutation/subset/combination solutions that differ from the ones introduced here. This is because there are two perspectives in backtracking algorithm enumeration. I will explain these perspectives in detail later in Ball and Box Model: Two Perspectives of Backtracking Algorithm Enumeration. For now, it is best to follow my approach.