Two Pointer Techniques for Linked List Problems
This article will resolve
This article summarizes the basic techniques of singly linked lists. Each technique matches at least one algorithm problem:
Merge two sorted linked lists
Split a linked list
Merge
ksorted linked listsFind the k-th node from the end of a linked list
Find the middle node of a linked list
Check if a linked list has a cycle and find the cycle's starting point
Check if two singly linked lists intersect and find the intersection node
All these solutions use the two-pointer technique. So, for linked list problems, two pointers are very common. Let's look at them one by one.
Merge Two Sorted Linked Lists
This is the most basic linked list technique. LeetCode problem 21 "Merge Two Sorted Lists" is about this. You are given two sorted linked lists. Please merge them into one new sorted linked list:
21. Merge Two Sorted Lists | LeetCode | 🟢
You are given the heads of two sorted linked lists list1 and list2.
Merge the two lists into one sorted list. The list should be made by splicing together the nodes of the first two lists.
Return the head of the merged linked list.
Example 1:
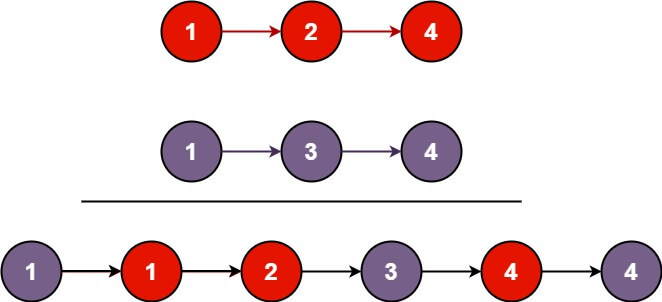
Input: list1 = [1,2,4], list2 = [1,3,4] Output: [1,1,2,3,4,4]
Example 2:
Input: list1 = [], list2 = [] Output: []
Example 3:
Input: list1 = [], list2 = [0] Output: [0]
Constraints:
- The number of nodes in both lists is in the range
[0, 50]. -100 <= Node.val <= 100- Both
list1andlist2are sorted in non-decreasing order.
// The function signature is as follows
ListNode mergeTwoLists(ListNode l1, ListNode l2);// The function signature is as follows
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2);# The function signature is as follows
def mergeTwoLists(l1: ListNode, l2: ListNode) -> ListNode:// The function signature is as follows
func mergeTwoLists(l1 *ListNode, l2 *ListNode) *ListNode {}// the function signature is as follows
var mergeTwoLists = function(l1, l2) {}This problem is simple. Let's look at the solution:
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
// dummy head node
ListNode dummy = new ListNode(-1), p = dummy;
ListNode p1 = l1, p2 = l2;
while (p1 != null && p2 != null) { // compare two pointers p1 and p2
// attach the node with the smaller value to the p pointer
if (p1.val > p2.val) {
p.next = p2;
p2 = p2.next;
} else {
p.next = p1;
p1 = p1.next;
}
// the p pointer moves forward continuously
p = p.next;
}
if (p1 != null) {
p.next = p1;
}
if (p2 != null) {
p.next = p2;
}
return dummy.next;
}
}
// compare two pointers p1 and p2
// attach the node with the smaller value to the p pointer
if (p1.val > p2.val) {
p.next = p2;
p2 = p2.next;
} else {
p.next = p1;
p1 = p1.next;
}
// the p pointer moves forward continuously
p = p.next;
}
if (p1 != null) {
p.next = p1;
}
if (p2 != null) {
p.next = p2;
}
return dummy.next;
}
}class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
// dummy head node
ListNode dummy(-1), *p = &dummy;
ListNode *p1 = l1, *p2 = l2;
while (p1 != nullptr && p2 != nullptr) { // compare the two pointers p1 and p2
// attach the node with the smaller value to the pointer p
if (p1->val > p2->val) {
p->next = p2;
p2 = p2->next;
} else {
p->next = p1;
p1 = p1->next;
}
// advance the pointer p continuously
p = p->next;
}
if (p1 != nullptr) {
p->next = p1;
}
if (p2 != nullptr) {
p->next = p2;
}
return dummy.next;
}
};
// compare the two pointers p1 and p2
// attach the node with the smaller value to the pointer p
if (p1->val > p2->val) {
p->next = p2;
p2 = p2->next;
} else {
p->next = p1;
p1 = p1->next;
}
// advance the pointer p continuously
p = p->next;
}
if (p1 != nullptr) {
p->next = p1;
}
if (p2 != nullptr) {
p->next = p2;
}
return dummy.next;
}
};class Solution:
def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
# dummy head node
dummy = ListNode(-1)
p = dummy
p1 = l1
p2 = l2
while p1 is not None and p2 is not None:  # compare the two pointers p1 and p2
# attach the node with the smaller value to the p pointer
if p1.val > p2.val:
p.next = p2
p2 = p2.next
else:
p.next = p1
p1 = p1.next
# the p pointer keeps moving forward
p = p.next
if p1 is not None:
p.next = p1
if p2 is not None:
p.next = p2
return dummy.next
# compare the two pointers p1 and p2
# attach the node with the smaller value to the p pointer
if p1.val > p2.val:
p.next = p2
p2 = p2.next
else:
p.next = p1
p1 = p1.next
# the p pointer keeps moving forward
p = p.next
if p1 is not None:
p.next = p1
if p2 is not None:
p.next = p2
return dummy.nextfunc mergeTwoLists(l1 *ListNode, l2 *ListNode) *ListNode {
// dummy head node
dummy := &ListNode{-1, nil}
p := dummy
p1 := l1
p2 := l2
for p1 != nil && p2 != nil { // compare pointers p1 and p2
// attach the node with the smaller value to the p pointer
if p1.Val > p2.Val {
p.Next = p2
p2 = p2.Next
} else {
p.Next = p1
p1 = p1.Next
}
// advance the p pointer
p = p.Next
}
if p1 != nil {
p.Next = p1
}
if p2 != nil {
p.Next = p2
}
return dummy.Next
}
// compare pointers p1 and p2
// attach the node with the smaller value to the p pointer
if p1.Val > p2.Val {
p.Next = p2
p2 = p2.Next
} else {
p.Next = p1
p1 = p1.Next
}
// advance the p pointer
p = p.Next
}
if p1 != nil {
p.Next = p1
}
if p2 != nil {
p.Next = p2
}
return dummy.Next
}var mergeTwoLists = function(l1, l2) {
// virtual head node
var dummy = new ListNode(-1), p = dummy;
var p1 = l1, p2 = l2;
while (p1 !== null && p2 !== null) { // compare the two pointers p1 and p2
// attach the node with the smaller value to the pointer p
if (p1.val > p2.val) {
p.next = p2;
p2 = p2.next;
} else {
p.next = p1;
p1 = p1.next;
}
// the p pointer keeps moving forward
p = p.next;
}
if (p1 !== null) {
p.next = p1;
}
if (p2 !== null) {
p.next = p2;
}
return dummy.next;
};
// compare the two pointers p1 and p2
// attach the node with the smaller value to the pointer p
if (p1.val > p2.val) {
p.next = p2;
p2 = p2.next;
} else {
p.next = p1;
p1 = p1.next;
}
// the p pointer keeps moving forward
p = p.next;
}
if (p1 !== null) {
p.next = p1;
}
if (p2 !== null) {
p.next = p2;
}
return dummy.next;
};Our while loop compares p1 and p2 each time. The smaller node is added to the result list. See the following GIF:

To understand it, this algorithm works like zipping up a zipper. l1 and l2 are like the two sides of the zipper teeth. The pointer p is like the zipper puller, merging two sorted linked lists together.
Below is a visualization of the algorithm. You can click the line while (p1 != null && p2 != null) many times to see how p merges the two sorted linked lists:
Algorithm Visualization
The code also uses a common trick in linked list problems called the "dummy node" or virtual head node, which is the dummy node. If you try not using the dummy node, the code gets more complex and you need to handle when pointer p is null. With the dummy node as a placeholder, you can avoid handling null pointers and keep the code simple.
When to Use a Dummy Node
Many readers ask me, when should we use a dummy (virtual head) node? Here is my summary: When you need to create a new linked list, you can use a dummy node to make edge cases easier.
For example, when you merge two sorted lists into a new list, you need to create a new linked list. Or when you split a list into two new lists, you are also creating new linked lists. In these cases, using a dummy node makes the code simpler and easier to handle edge cases.
Decomposing a Singly Linked List
Let's look at LeetCode Problem 86: Partition List:
86. Partition List | LeetCode | 🟠
Given the head of a linked list and a value x, partition it such that all nodes less than x come before nodes greater than or equal to x.
You should preserve the original relative order of the nodes in each of the two partitions.
Example 1:
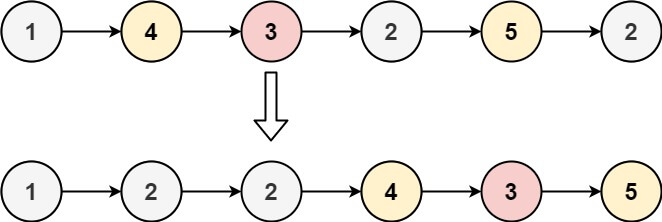
Input: head = [1,4,3,2,5,2], x = 3 Output: [1,2,2,4,3,5]
Example 2:
Input: head = [2,1], x = 2 Output: [1,2]
Constraints:
- The number of nodes in the list is in the range
[0, 200]. -100 <= Node.val <= 100-200 <= x <= 200
When merging two sorted linked lists, you combine them into one. Here, you need to split the original list into two. Specifically, you can divide the original list into two smaller lists: one list with elements less than x, and another with elements greater than or equal to x. In the end, connect these two lists together to get the result the problem wants.
The overall logic is very similar to merging sorted lists. For the details, let's look at the code. Pay attention to how we use dummy head nodes:
class Solution {
public ListNode partition(ListNode head, int x) {
// dummy head for the list storing nodes less than x
ListNode dummy1 = new ListNode(-1);
// dummy head for the list storing nodes greater than or equal to x
ListNode dummy2 = new ListNode(-1);
// p1, p2 pointers are responsible for generating the result list
ListNode p1 = dummy1, p2 = dummy2;
// p is responsible for traversing the original list,
// similar to the logic of merging two sorted lists
// here, we decompose one list into two lists
ListNode p = head;
while (p != null) {
if (p.val >= x) {
p2.next = p;
p2 = p2.next;
} else {
p1.next = p;
p1 = p1.next;
}
// break the next pointer of each node in the original list
ListNode temp = p.next;
p.next = null;
p = temp;
}
// link the two lists
p1.next = dummy2.next;
return dummy1.next;
}
}class Solution {
public:
ListNode* partition(ListNode* head, int x) {
// virtual head node for the list storing nodes less than x
ListNode* dummy1 = new ListNode(-1);
// virtual head node for the list storing nodes greater than or equal to x
ListNode* dummy2 = new ListNode(-1);
// p1, p2 pointers responsible for generating the result list
ListNode* p1 = dummy1, *p2 = dummy2;
// p is responsible for traversing the original list,
// similar to the logic of merging two sorted lists
// here we decompose a list into two lists
ListNode* p = head;
while (p != nullptr) {
if (p->val >= x) {
p2->next = p;
p2 = p2->next;
} else {
p1->next = p;
p1 = p1->next;
}
// cannot directly advance the p pointer,
// p = p->next
// disconnect the next pointer of each node in the original list
ListNode* temp = p->next;
p->next = nullptr;
p = temp;
}
// connect the two lists
p1->next = dummy2->next;
return dummy1->next;
}
};class Solution:
def partition(self, head: ListNode, x: int) -> ListNode:
# virtual head node for the list containing elements less than x
dummy1 = ListNode(-1)
# virtual head node for the list containing elements greater than or equal to x
dummy2 = ListNode(-1)
# p1, p2 pointers are responsible for creating the resulting list
p1, p2 = dummy1, dummy2
# p is responsible for traversing the original list,
# similar to the logic of merging two sorted lists
# here we decompose one list into two lists
p = head
while p:
if p.val >= x:
p2.next = p
p2 = p2.next
else:
p1.next = p
p1 = p1.next
# cannot directly move the p pointer forward,
# p = p.next
# break the next pointer of each node in the original list
temp = p.next
p.next = None
p = temp
# connect the two lists
p1.next = dummy2.next
return dummy1.nextfunc partition(head *ListNode, x int) *ListNode {
// virtual head node for the list storing nodes less than x
dummy1 := &ListNode{-1, nil}
// virtual head node for the list storing nodes greater than or equal to x
dummy2 := &ListNode{-1, nil}
// pointers p1 and p2 are responsible for generating the result list
p1, p2 := dummy1, dummy2
// pointer p is responsible for traversing the
// original list, similar to merging two sorted lists
// here we split one list into two lists
p := head
for p != nil {
if p.Val >= x {
p2.Next = p
p2 = p2.Next
} else {
p1.Next = p
p1 = p1.Next
}
// cannot move the p pointer forward directly,
// p = p.Next
// break the next pointer of each node in the original list
temp := p.Next
p.Next = nil
p = temp
}
// connect the two lists
p1.Next = dummy2.Next
return dummy1.Next
}var partition = function(head, x) {
// dummy head node for the list with nodes less than x
let dummy1 = new ListNode(-1);
// dummy head node for the list with nodes greater than or equal to x
let dummy2 = new ListNode(-1);
// p1 and p2 pointers are responsible for creating the result lists
let p1 = dummy1, p2 = dummy2;
// p is responsible for traversing the original list,
// similar to the logic of merging two sorted lists
// here we split the list into two lists
let p = head;
while (p !== null) {
if (p.val >= x) {
p2.next = p;
p2 = p2.next;
} else {
p1.next = p;
p1 = p1.next;
}
// cannot directly advance the p pointer,
// p = p.next
// break the next pointer of each node in the original list
let temp = p.next;
p.next = null;
p = temp;
}
// connect the two lists
p1.next = dummy2.next;
return dummy1.next;
};I know many readers may have questions about this part of the code:
// You cannot just move the p pointer forward like this:
// p = p.next
// You must break the next pointer of each node in the original list
ListNode temp = p.next;
p.next = null;
p = temp;Let's use our visual panel to understand this. First, look at the correct way. Click the line while (p !== null) several times to see how the list is split:
Algorithm Visualization
If you do not break the next pointer of each node in the original list, it will go wrong. The result list will include a cycle. You can click while (p !== null) several times to see:
Algorithm Visualization
In summary, if we want to attach nodes from the original list to a new list, instead of creating new nodes, it is often necessary to break the link between the node and the original list. It's a good habit: in such cases, always disconnect the node from the original list to avoid mistakes.
Merge k Sorted Linked Lists
Let's look at LeetCode Problem 23: Merge k Sorted Lists:
23. Merge k Sorted Lists | LeetCode | 🔴
You are given an array of k linked-lists lists, each linked-list is sorted in ascending order.
Merge all the linked-lists into one sorted linked-list and return it.
Example 1:
Input: lists = [[1,4,5],[1,3,4],[2,6]] Output: [1,1,2,3,4,4,5,6] Explanation: The linked-lists are: [ 1->4->5, 1->3->4, 2->6 ] merging them into one sorted list: 1->1->2->3->4->4->5->6
Example 2:
Input: lists = [] Output: []
Example 3:
Input: lists = [[]] Output: []
Constraints:
k == lists.length0 <= k <= 1040 <= lists[i].length <= 500-104 <= lists[i][j] <= 104lists[i]is sorted in ascending order.- The sum of
lists[i].lengthwill not exceed104.
// The function signature is as follows
ListNode mergeKLists(ListNode[] lists);// The function signature is as follows
ListNode* mergeKLists(vector<ListNode*>& lists);# The function signature is as follows
def mergeKLists(lists: List[ListNode]) -> ListNode:// The function signature is as follows
func mergeKLists(lists []*ListNode) *ListNode// The function signature is as follows
var mergeKLists = function(lists) {};Merging k sorted linked lists is similar to merging two sorted lists. The main challenge is: how to quickly get the smallest node among the k nodes and add it to the result list?
Here, we use a priority queue. Put the nodes into a min-heap, and you can always get the smallest node among the k nodes. If you want to know more about priority queues, see Priority Queue (Binary Heap) Principle and Implementation. This article will not go into details.
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
if (lists.length == 0) return null;
// dummy head node
ListNode dummy = new ListNode(-1);
ListNode p = dummy;
// priority queue, min-heap
PriorityQueue<ListNode> pq = new PriorityQueue<>(
lists.length, (a, b)->(a.val - b.val));
// add the head nodes of the k linked lists into the min-heap
for (ListNode head : lists) {
if (head != null)
pq.add(head);
}
while (!pq.isEmpty()) {
// get the smallest node and attach it to the result list
ListNode node = pq.poll();
p.next = node;
if (node.next != null) {
pq.add(node.next);
}
// move the p pointer forward
p = p.next;
}
return dummy.next;
}
}class Solution {
public:
ListNode* mergeKLists(vector<ListNode*>& lists) {
if (lists.empty()) return nullptr;
// dummy head node
ListNode* dummy = new ListNode(-1);
ListNode* p = dummy;
// priority queue, min-heap
auto cmp = [](ListNode* a, ListNode* b) { return a->val > b->val; };
priority_queue<ListNode*, vector<ListNode*>, decltype(cmp)> pq(cmp);
// add the head nodes of k linked lists to the min-heap
for (ListNode* head : lists) {
if (head != nullptr) {
pq.push(head);
}
}
while (!pq.empty()) {
// get the smallest node and attach it to the result linked list
ListNode* node = pq.top();
pq.pop();
p->next = node;
if (node->next != nullptr) {
pq.push(node->next);
}
// move the p pointer forward continuously
p = p->next;
}
return dummy->next;
}
};import heapq
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
# Override comparison operators to facilitate adding ListNode to the min-heap
def __lt__(self, other):
return self.val < other.val
class Solution:
def mergeKLists(self, lists):
if not lists:
return None
# Dummy head node
dummy = ListNode(-1)
p = dummy
# Priority queue, min-heap
pq = []
# Add the head nodes of k linked lists to the min-heap
for i, head in enumerate(lists):
if head is not None:
heapq.heappush(pq, (head.val, i, head))
while pq:
# Get the smallest node and attach it to the result linked list
val, i, node = heapq.heappop(pq)
p.next = node
if node.next is not None:
heapq.heappush(pq, (node.next.val, i, node.next))
# Move the p pointer forward continuously
p = p.next
return dummy.nextimport "container/heap"
// Implement heap.Interface for ListNode
type PriorityQueue []*ListNode
func (pq PriorityQueue) Len() int { return len(pq) }
func (pq PriorityQueue) Less(i, j int) bool {
return pq[i].Val < pq[j].Val
}
func (pq PriorityQueue) Swap(i, j int) {
pq[i], pq[j] = pq[j], pq[i]
}
func (pq *PriorityQueue) Push(x interface{}) {
*pq = append(*pq, x.(*ListNode))
}
func (pq *PriorityQueue) Pop() interface{} {
old := *pq
n := len(old)
x := old[n-1]
*pq = old[0 : n-1]
return x
}
func mergeKLists(lists []*ListNode) *ListNode {
if len(lists) == 0 {
return nil
}
// dummy head node
dummy := &ListNode{Val: -1}
p := dummy
// priority queue, min-heap
pq := &PriorityQueue{}
heap.Init(pq)
// add the head nodes of the k linked lists to the min-heap
for _, head := range lists {
if head != nil {
heap.Push(pq, head)
}
}
for pq.Len() > 0 {
// get the smallest node and attach it to the result linked list
node := heap.Pop(pq).(*ListNode)
p.Next = node
if node.Next != nil {
heap.Push(pq, node.Next)
}
// move the p pointer forward continuously
p = p.Next
}
return dummy.Next
}var mergeKLists = function(lists) {
if (lists.length === 0) return null;
// virtual head node
var dummy = new ListNode(-1);
var p = dummy;
// priority queue, min heap
var pq = new MinPriorityQueue({ priority: (node) => node.val });
// add the head nodes of the k linked lists to the min heap
for (var i = 0; i < lists.length; i++) {
if (lists[i] !== null) {
pq.enqueue(lists[i]);
}
}
while (!pq.isEmpty()) {
// get the smallest node and attach it to the result linked list
var node = pq.dequeue().element;
p.next = node;
if (node.next !== null) {
pq.enqueue(node.next);
}
// p pointer keeps moving forward
p = p.next;
}
return dummy.next;
}You can open the visual panel below and click the line while (pq.size() > 0) several times to see the process of merging sorted lists:
Algorithm Visualization
This algorithm is a common interview question. What is its time complexity?
The priority queue pq can hold at most elements, so each poll or add operation takes time. All nodes from all lists are added and removed from pq, so the total time complexity is , where is the number of lists and is the total number of nodes.
Tip
There is another classic solution for this problem, explained in detail in Divide and Conquer Algorithm Framework. We will not discuss it here.
The k-th Node from the End of a Singly Linked List
It is easy to find the k-th node from the start of a singly linked list. You just use a for loop to move forward and find it. But how do you find the k-th node from the end?
You might say, if the linked list has n nodes, the k-th node from the end is the (n - k + 1)-th node from the start. You could just use a for loop too.
That's correct. But in algorithm problems, you are usually only given the head node of the linked list. You don't know the length n. You need to first walk through the list once to find n, and then walk through it again to find the (n - k + 1)-th node.
This solution needs to traverse the list twice to get the k-th node from the end.
Can we find the k-th node from the end with just one pass? Yes, we can. In interviews, the interviewer usually wants you to solve it with just one traversal.
Here is a clever way. Let’s say k = 2. The idea is:
First, let a pointer p1 point to the head node. Move p1 forward k steps:
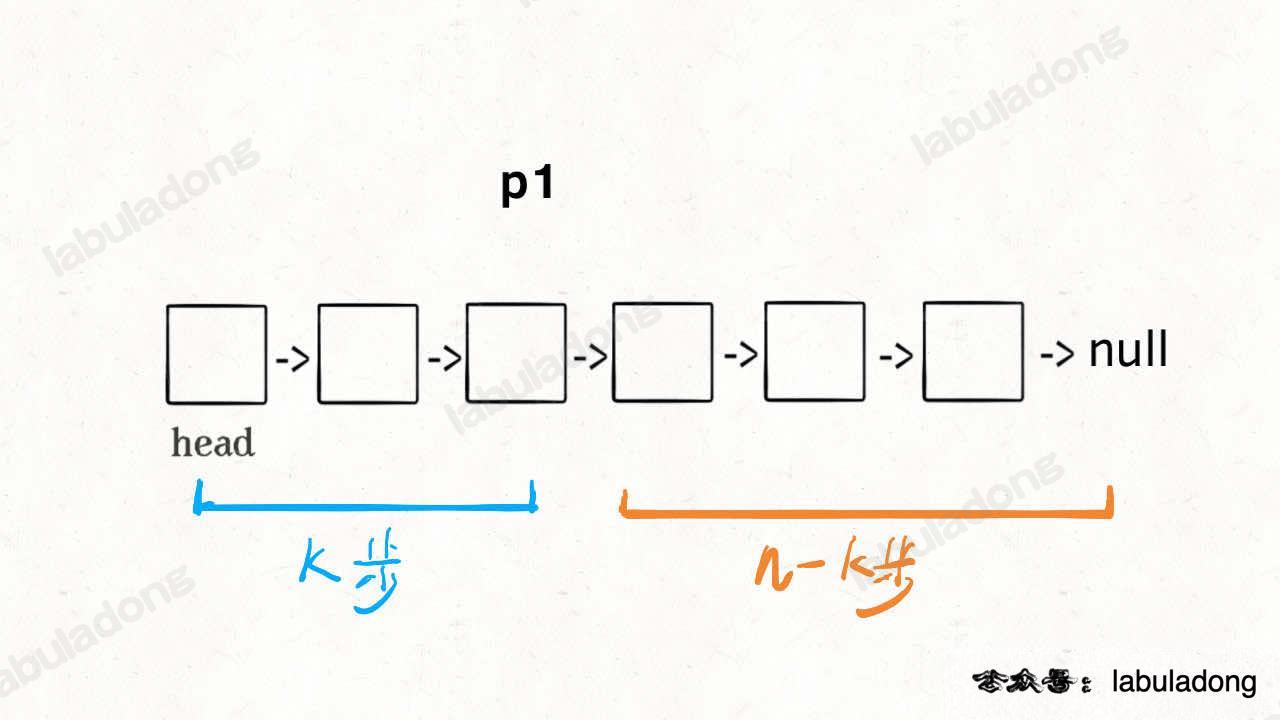
Now, p1 needs to move (n - k) more steps to reach the end of the list.
At this moment, use another pointer p2, and let it also point to the head node:
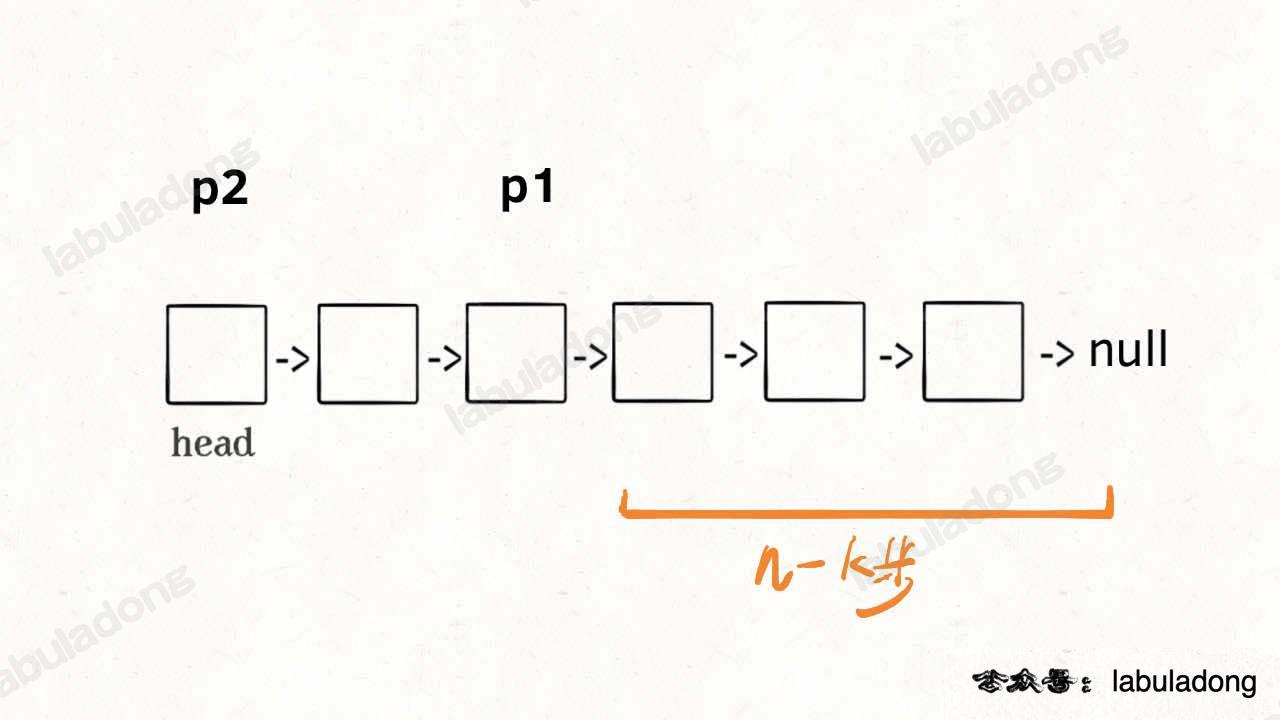
Now, move p1 and p2 forward at the same time. When p1 reaches the end (null), it has moved (n - k) steps. p2 also moves (n - k) steps from the head, which means it is now at the (n - k + 1)-th node. That is the k-th node from the end:
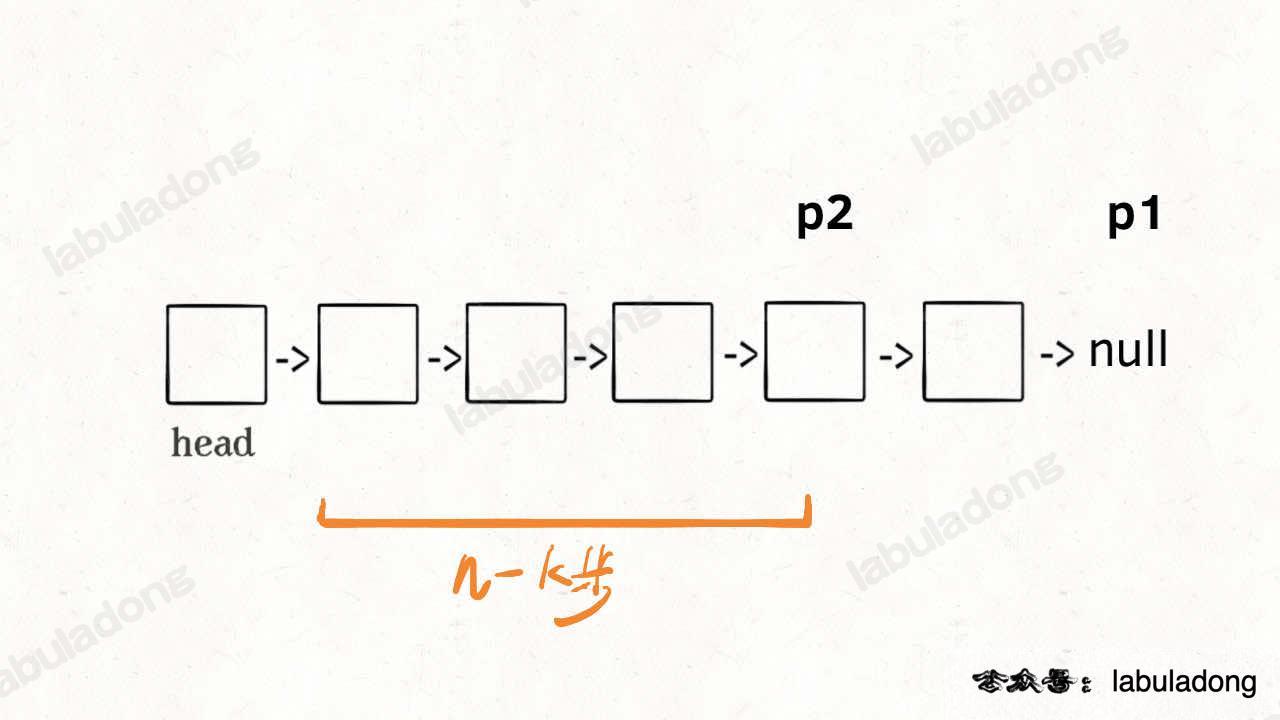
This way, you find the k-th node from the end by traversing the list only once. p2 is your answer.
Here is the code for this logic:
// return the k-th node from the end of the linked list
ListNode findFromEnd(ListNode head, int k) {
ListNode p1 = head;
// p1 moves k steps first
for (int i = 0; i < k; i++) {
p1 = p1.next;
}
ListNode p2 = head;
// p1 and p2 move n - k steps together
while (p1 != null) {
p2 = p2.next;
p1 = p1.next;
}
// p2 is now pointing to the (n - k + 1)-th node, which is the k-th node from the end
return p2;
}// return the k-th node from the end of the linked list
ListNode* findFromEnd(ListNode* head, int k) {
ListNode* p1 = head;
// p1 moves k steps first
for (int i = 0; i < k; i++) {
p1 = p1 -> next;
}
ListNode* p2 = head;
// p1 and p2 move n - k steps together
while (p1 != nullptr) {
p2 = p2 -> next;
p1 = p1 -> next;
}
// p2 now points to the (n - k + 1)-th node, which is the k-th node from the end
return p2;
}# return the k-th node from the end of the linked list
def findFromEnd(head: ListNode, k: int) -> ListNode:
p1 = head
# p1 goes k steps first
for i in range(k):
p1 = p1.next
p2 = head
# p1 and p2 go n - k steps together
while p1 != None:
p2 = p2.next
p1 = p1.next
# p2 now points to the (n - k + 1)-th node, which is the k-th node from the end
return p2// return the k-th node from the end of the linked list
func findFromEnd(head *ListNode, k int) *ListNode {
p1 := head
// p1 moves k steps forward
for i := 0; i < k; i++ {
p1 = p1.Next
}
p2 := head
// p1 and p2 move n - k steps together
for p1 != nil {
p1 = p1.Next
p2 = p2.Next
}
// p2 now points to the (n - k + 1)-th node, which is the k-th node from the end
return p2
}// return the k-th node from the end of the linked list
var findFromEnd = function(head, k) {
var p1 = head;
// p1 moves k steps first
for (var i = 0; i < k; i++) {
p1 = p1.next;
}
var p2 = head;
// p1 and p2 move together n - k steps
while (p1 != null) {
p2 = p2.next;
p1 = p1.next;
}
// p2 now points to the (n - k + 1)-th node, which is the k-th node from the end
return p2;
};You can open the visual panel below. The code will calculate the second node from the end. Click i++ several times to see the fast pointer p1 move ahead 2 steps. Then, click while (p1 !== null) several times to watch p1 and p2 move forward together. In the end, p2 stops at the k-th node from the end.
Algorithm Visualization
If we use big O notation, the time complexity is O(N) for both the two-pass and the one-pass solutions. But the one-pass solution is more clever.
Many linked list problems use this trick. For example, LeetCode Problem 19: "Remove Nth Node From End of List":
19. Remove Nth Node From End of List | LeetCode | 🟠
Given the head of a linked list, remove the nth node from the end of the list and return its head.
Example 1:
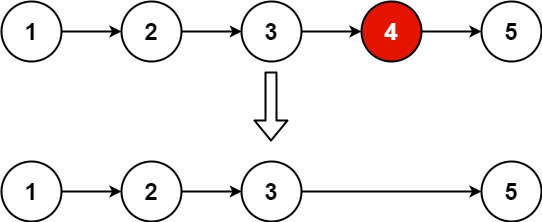
Input: head = [1,2,3,4,5], n = 2 Output: [1,2,3,5]
Example 2:
Input: head = [1], n = 1 Output: []
Example 3:
Input: head = [1,2], n = 1 Output: [1]
Constraints:
- The number of nodes in the list is
sz. 1 <= sz <= 300 <= Node.val <= 1001 <= n <= sz
Follow up: Could you do this in one pass?
Let's look at the code:
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
// virtual head node
ListNode dummy = new ListNode(-1);
dummy.next = head;
// to remove the nth node from the end, first find the (n + 1)th node from the end
ListNode x = findFromEnd(dummy, n + 1);
// remove the nth node from the end
x.next = x.next.next;
return dummy.next;
}
private ListNode findFromEnd(ListNode head, int k) {
// see the previous code
}
}class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
// dummy head node
ListNode* dummy = new ListNode(-1);
dummy->next = head;
// to delete the nth node from the end, first find the (n + 1)th node from the end
ListNode* x = findFromEnd(dummy, n + 1);
// delete the nth node from the end
x->next = x->next->next;
return dummy->next;
}
private:
ListNode* findFromEnd(ListNode* head, int k) {
// code is shown above
}
};# main function
class Solution:
def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
# dummy head node
dummy = ListNode(-1)
dummy.next = head
# to remove the nth from end, first find the (n + 1)th node from end
x = self.findFromEnd(dummy, n + 1)
# remove the nth node from end
x.next = x.next.next
return dummy.next
def findFromEnd(self, head: ListNode, k: int) -> ListNode:
# refer to the code above
passfunc removeNthFromEnd(head *ListNode, n int) *ListNode {
// virtual head node
dummy := &ListNode{Val: -1}
dummy.Next = head
// to delete the nth node from the end, first find the (n+1)th node from the end
x := findFromEnd(dummy, n+1)
// delete the nth node from the end
x.Next = x.Next.Next
return dummy.Next
}
func findFromEnd(head *ListNode, k int) *ListNode {
// code is shown above
}// main function
var removeNthFromEnd = function(head, n) {
// virtual head node
let dummy = new ListNode(-1);
dummy.next = head;
// to remove the nth node from the end, first find the (n + 1)th node from the end
let x = findFromEnd(dummy, n + 1);
// remove the nth node from the end
x.next = x.next.next;
return dummy.next;
};
var findFromEnd = function(head, k) {
// code is in the previous text
};You can open the visual panel. Click let p2 = head; once to see p2 move k steps forward. Then, click while (p1 !== null) several times to watch p1 and p2 move forward together. In the end, p2 stops at the k-th node from the end.
Algorithm Visualization
This logic is simple. To delete the n-th node from the end, you need to get the reference to the (n + 1)-th node from the end. You can use our findFromEnd function for this.
Notice we use a dummy node (virtual head) trick. This helps avoid null pointer problems. For example, if the list has 5 nodes and you need to delete the 5th node from the end (the first node), you need to find the 6th node from the end. But there is no node before the head, so you will have an error.
With the dummy node, you can avoid this problem and handle all cases smoothly.
Middle Node of a Singly Linked List
LeetCode problem 876 "Middle of the Linked List" is about this topic. The main problem is that we cannot directly get the length n of the linked list. The normal way is to first go through the list to count n, and then go through again to get the n / 2-th node, which is the middle node.
If you want to find the middle node in one pass, you need to use a smart trick called the "fast and slow pointer" technique:
We use two pointers, slow and fast, both starting at the head of the list.
Every time the slow pointer slow moves one step, the fast pointer fast moves two steps. This way, when fast reaches the end of the list, slow will be at the middle node.
Here is the code for this idea:
class Solution {
public ListNode middleNode(ListNode head) {
// initialize slow and fast pointers to head
ListNode slow = head, fast = head;
// stop when the fast pointer reaches the end
while (fast != null && fast.next != null) {
// slow pointer moves one step, fast pointer moves two steps
slow = slow.next;
fast = fast.next.next;
}
// slow pointer points to the middle node
return slow;
}
}class Solution {
public:
ListNode* middleNode(ListNode* head) {
// initialize slow and fast pointers to head
ListNode* slow = head;
ListNode* fast = head;
// stop when the fast pointer reaches the end
while (fast != nullptr && fast->next != nullptr) {
// slow pointer moves one step, fast pointer moves two steps
slow = slow->next;
fast = fast->next->next;
}
// slow pointer points to the middle node
return slow;
}
};class Solution:
# initialize slow and fast pointers to head
def middleNode(self, head: ListNode) -> ListNode:
slow = head
fast = head
# stop when the fast pointer reaches the end
while fast is not None and fast.next is not None:
# slow pointer moves one step, fast pointer moves two steps
slow = slow.next
fast = fast.next.next
# slow pointer points to the middle node
return slowfunc middleNode(head *ListNode) *ListNode {
// initialize slow and fast pointers to head
slow, fast := head, head
// stop when the fast pointer reaches the end
for fast != nil && fast.Next != nil {
// slow pointer moves one step, fast pointer moves two steps
slow = slow.Next
fast = fast.Next.Next
}
// slow pointer points to the middle node
return slow
}var middleNode = function(head) {
// initialize slow and fast pointers to head
let slow = head, fast = head;
// stop when the fast pointer reaches the end
while (fast !== null && fast.next !== null) {
// slow pointer moves one step, fast pointer moves two steps
slow = slow.next;
fast = fast.next.next;
}
// slow pointer points to the middle node
return slow;
};You can open the visual panel and click on the line while (fast !== null && fast.next !== null) to see how the fast and slow pointers move:
Algorithm Visualization
Note: If the length of the list is even (there are two middle nodes), this method will return the second one.
Also, you can change this code a little to solve the problem of checking if a linked list has a cycle.
Check if a Linked List Has a Cycle
Checking if a linked list has a cycle is a classic problem. The solution also uses the fast and slow pointer method:
Every time the slow pointer slow moves one step, the fast pointer fast moves two steps.
If fast can reach the end of the list, then there is no cycle. If fast meets slow while moving, then fast must be running in a circle, so the list has a cycle.
You just need to change the code for finding the middle node a little:
public class Solution {
public boolean hasCycle(ListNode head) {
// initialize slow and fast pointers to head
ListNode slow = head, fast = head;
// stop when the fast pointer reaches the end
while (fast != null && fast.next != null) {
// slow pointer moves one step, fast pointer moves two steps
slow = slow.next;
fast = fast.next.next;
// if slow and fast pointers meet, it indicates a cycle
if (slow == fast) {
return true;
}
}
// no cycle present
return false;
}
}class Solution {
public:
bool hasCycle(ListNode *head) {
// initialize slow and fast pointers to head
ListNode *slow = head, *fast = head;
// stop when the fast pointer reaches the end
while (fast != nullptr && fast->next != nullptr) {
// slow pointer moves one step, fast pointer moves two steps
slow = slow->next;
fast = fast->next->next;
// if slow and fast pointers meet, it indicates a cycle
if (slow == fast) {
return true;
}
}
// no cycle present
return false;
}
};class Solution:
# initialize slow and fast pointers to head
def hasCycle(self, head: ListNode) -> bool:
slow = head
fast = head
# stop when the fast pointer reaches the end
while fast is not None and fast.next is not None:
# slow pointer moves one step, fast pointer moves two steps
slow = slow.next
fast = fast.next.next
# if slow and fast pointers meet, it indicates a cycle
if slow == fast:
return True
# no cycle present
return Falsefunc hasCycle(head *ListNode) bool {
// initialize slow and fast pointers to head
slow, fast := head, head
// stop when the fast pointer reaches the end
for fast != nil && fast.Next != nil {
// slow pointer moves one step, fast pointer moves two steps
slow = slow.Next
fast = fast.Next.Next
// if slow and fast pointers meet, it indicates a cycle
if slow == fast {
return true
}
}
// no cycle present
return false
}var hasCycle = function(head) {
// initialize slow and fast pointers to head
let slow = head, fast = head;
// stop when the fast pointer reaches the end
while (fast !== null && fast.next !== null) {
// slow pointer moves one step, fast pointer moves two steps
slow = slow.next;
fast = fast.next.next;
// if slow and fast pointers meet, it indicates a cycle
if (slow === fast) {
return true;
}
}
// no cycle present
return false;
};You can open the visual panel below and click the line fast = fast.next.next; many times to see the movement of the pointers and how they finally meet:
Algorithm Visualization
There is also a harder version of this problem: LeetCode 142 "Linked List Cycle II": If there is a cycle, how do you find the start node of the cycle?
For example, the start of the cycle is node 2 in the picture below:
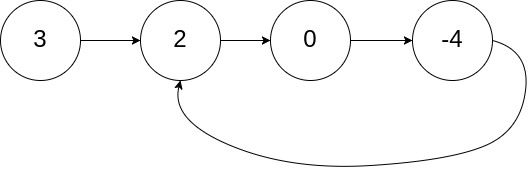
Here is the code to find the start of the cycle:
class Solution {
public ListNode detectCycle(ListNode head) {
ListNode fast, slow;
fast = slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) break;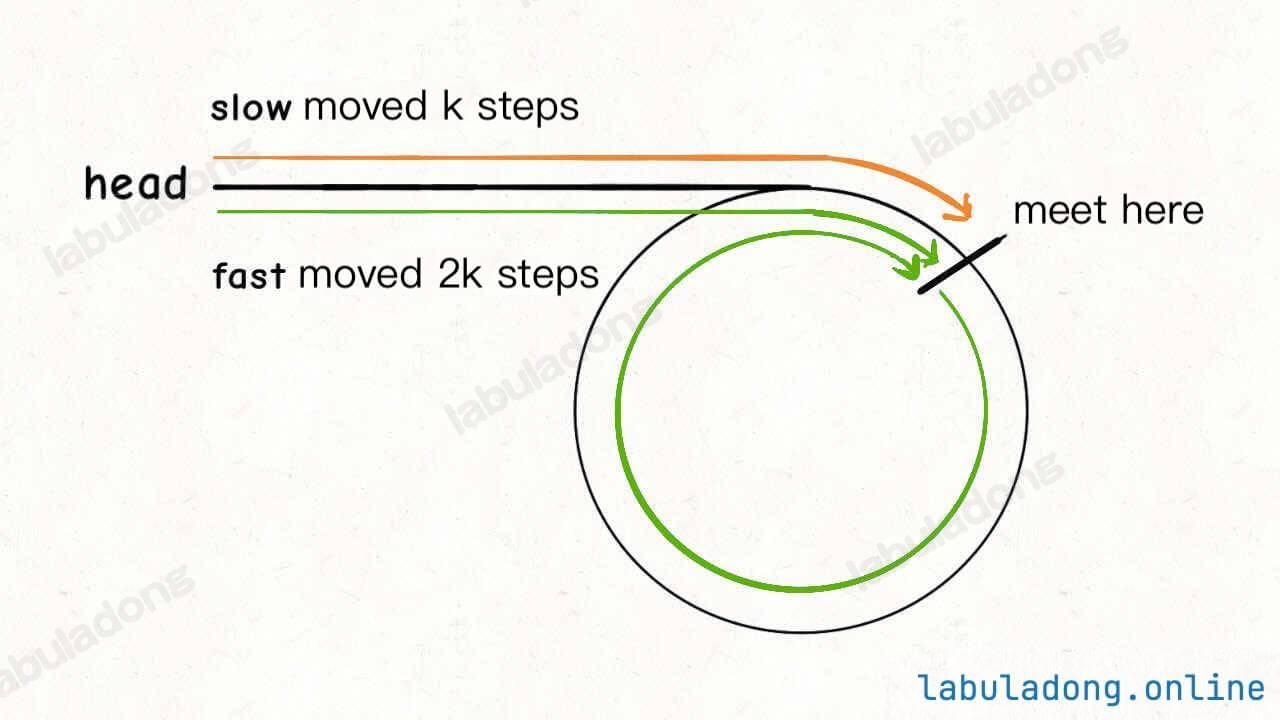 }
// the above code is similar to the hasCycle function
if (fast == null || fast.next == null) {
// fast encountering a null pointer means there is no cycle
return null;
}
// reassign to the head node
slow = head;
}
// the above code is similar to the hasCycle function
if (fast == null || fast.next == null) {
// fast encountering a null pointer means there is no cycle
return null;
}
// reassign to the head node
slow = head;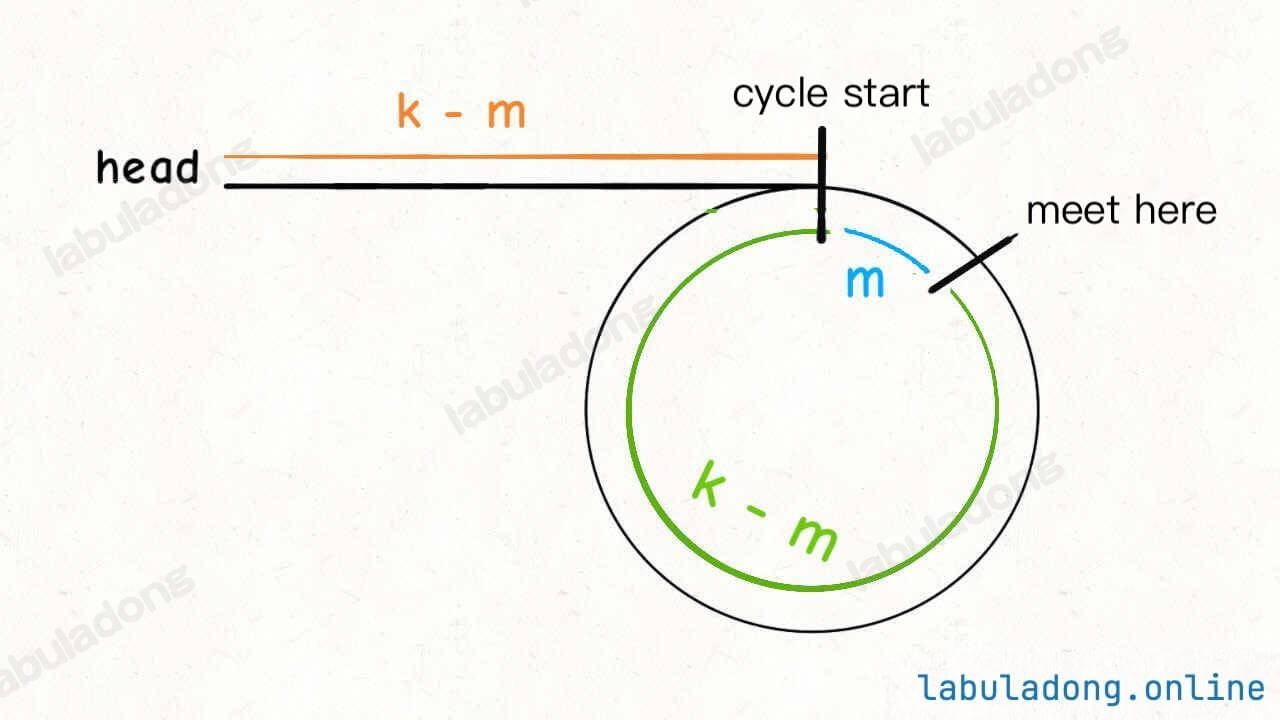 // move fast and slow pointers at the same pace, the
// intersection point is the cycle's entry point
while (slow != fast) {
fast = fast.next;
slow = slow.next;
}
return slow;
}
}
// move fast and slow pointers at the same pace, the
// intersection point is the cycle's entry point
while (slow != fast) {
fast = fast.next;
slow = slow.next;
}
return slow;
}
}class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode *fast, *slow;
fast = slow = head;
while (fast != nullptr && fast->next != nullptr) {
fast = fast->next->next;
slow = slow->next;
if (fast == slow) break; }
// the above code is similar to the hasCycle function
if (fast == nullptr || fast->next == nullptr) {
// if fast encounters a null pointer, it means there is no cycle
return nullptr;
}
// reset to the head node
slow = head;
}
// the above code is similar to the hasCycle function
if (fast == nullptr || fast->next == nullptr) {
// if fast encounters a null pointer, it means there is no cycle
return nullptr;
}
// reset to the head node
slow = head; // move the fast and slow pointers forward in sync, the
// intersection point is the start of the cycle
while (slow != fast) {
fast = fast->next;
slow = slow->next;
}
return slow;
}
};
// move the fast and slow pointers forward in sync, the
// intersection point is the start of the cycle
while (slow != fast) {
fast = fast->next;
slow = slow->next;
}
return slow;
}
};class Solution:
def detectCycle(self, head: ListNode):
fast, slow = head, head
while fast and fast.next:
fast = fast.next.next
slow = slow.next
if fast == slow:
break # the above code is similar to the hasCycle function
if not fast or not fast.next:
# if fast encounters a null pointer, it means there is no cycle
return None
# reset the pointer to the head node
slow = head
# the above code is similar to the hasCycle function
if not fast or not fast.next:
# if fast encounters a null pointer, it means there is no cycle
return None
# reset the pointer to the head node
slow = head  # both fast and slow pointers move forward in sync, the
# intersection point is the start of the cycle
while slow != fast:
fast = fast.next
slow = slow.next
return slow
# both fast and slow pointers move forward in sync, the
# intersection point is the start of the cycle
while slow != fast:
fast = fast.next
slow = slow.next
return slowfunc detectCycle(head *ListNode) *ListNode {
fast, slow := head, head
for fast != nil && fast.Next != nil {
fast = fast.Next.Next
slow = slow.Next
if fast == slow {
break }
}
// the above code is similar to the hasCycle function
if fast == nil || fast.Next == nil {
// if fast encounters a null pointer, it means there is no cycle
return nil
}
// reset the pointer to the head node
slow = head
}
}
// the above code is similar to the hasCycle function
if fast == nil || fast.Next == nil {
// if fast encounters a null pointer, it means there is no cycle
return nil
}
// reset the pointer to the head node
slow = head // move the fast and slow pointers forward in sync,
// the intersection point is the start of the cycle
for slow != fast {
fast = fast.Next
slow = slow.Next
}
return slow
}
// move the fast and slow pointers forward in sync,
// the intersection point is the start of the cycle
for slow != fast {
fast = fast.Next
slow = slow.Next
}
return slow
}var detectCycle = function(head) {
let fast, slow;
fast = slow = head;
while (fast !== null && fast.next !== null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) break; }
// the above code is similar to the hasCycle function
if (fast === null || fast.next === null) {
// if fast encounters a null pointer, it means there is no cycle
return null;
}
// reset the pointer to the head node
slow = head;
}
// the above code is similar to the hasCycle function
if (fast === null || fast.next === null) {
// if fast encounters a null pointer, it means there is no cycle
return null;
}
// reset the pointer to the head node
slow = head; // move the fast and slow pointers forward in sync,
// the intersection point is the start of the cycle
while (slow !== fast) {
fast = fast.next;
slow = slow.next;
}
return slow;
};
// move the fast and slow pointers forward in sync,
// the intersection point is the start of the cycle
while (slow !== fast) {
fast = fast.next;
slow = slow.next;
}
return slow;
};You can open the visual panel below and click the line fast = fast.next.next; many times to see how the fast and slow pointers chase and meet. Then click the line while (slow != fast) many times to see both pointers move at the same speed and finally meet at the start of the cycle:
Algorithm Visualization
When the fast and slow pointers meet, set one of them to the head node, then move both at the same speed. When they meet again, the node is the start of the cycle.
Why does this work? Here is a simple explanation.
Suppose when the fast and slow pointers meet, the slow pointer slow has walked k steps. The fast pointer fast must have walked 2k steps:

fast has walked k steps more than slow. These extra k steps mean that fast has run around the cycle, so k is a multiple of the cycle's length.
Suppose the distance from the meeting point to the cycle's start is m. According to the picture, the distance from the head to the start of the cycle is k - m. So, if you start from head and walk k - m steps, you will reach the start of the cycle.
Also, if you start from the meeting point and walk k - m steps, you will also reach the start of the cycle. Because, from the meeting point, after k steps, you will be back to the meeting point. So, after k - m steps, you will be at the start of the cycle:

So, just set one of the pointers to head, and move both pointers at the same speed. After k - m steps, they will meet at the start of the cycle.
Do Two Linked Lists Intersect
This is an interesting problem. It is also LeetCode 160: Intersection of Two Linked Lists. The function signature is as follows:
ListNode getIntersectionNode(ListNode headA, ListNode headB);ListNode* getIntersectionNode(ListNode* headA, ListNode* headB);def getIntersectionNode(headA: ListNode, headB: ListNode) -> ListNode:func getIntersectionNode(headA *ListNode, headB *ListNode) *ListNodevar getIntersectionNode = function(headA, headB)You are given the heads of two linked lists, headA and headB. These two lists may intersect.
If they intersect, your algorithm should return the node where they intersect. If they do not intersect, return null.
For example, if the input linked lists look like the picture below:
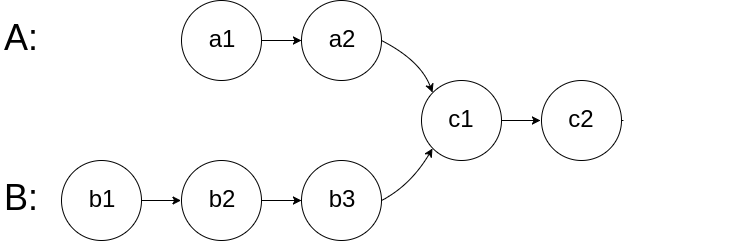
Your algorithm should return the node c1.
A direct idea is to use a HashSet to store all nodes of one list, then check the other list. But this needs extra space.
If you do not want to use extra space and only want to use two pointers, how can you do it?
The difficulty is that the two lists may have different lengths, so nodes cannot be matched one by one:
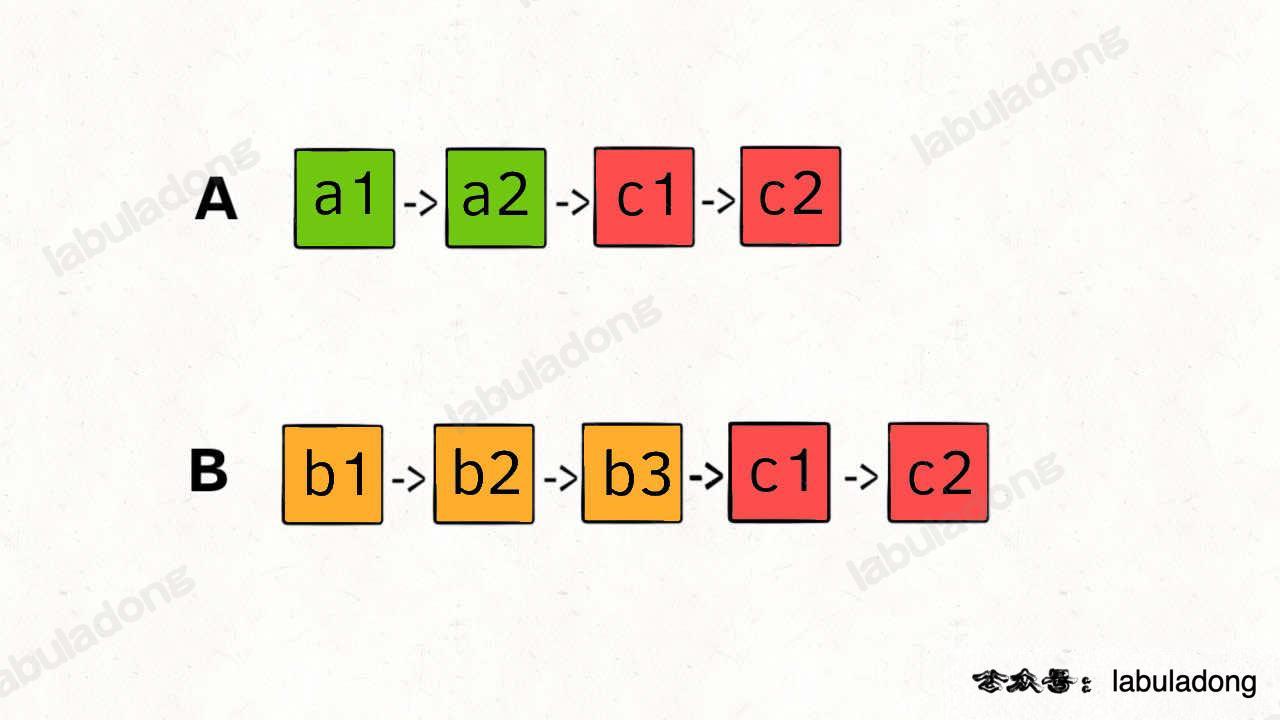
If you move two pointers, p1 and p2, along the lists, they cannot reach the intersection node at the same time. So you cannot get the intersection node c1.
The key is to find a way so that p1 and p2 can reach the intersection node c1 at the same time.
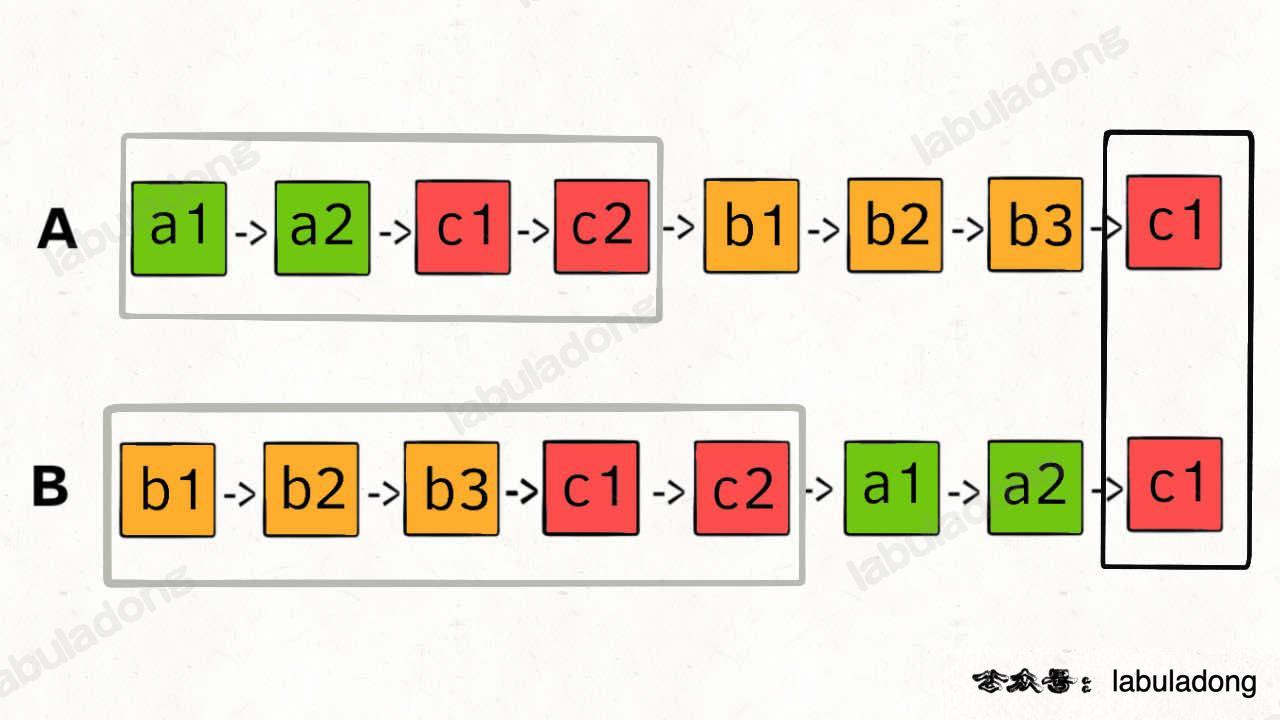
So, we can let p1 travel list A, then switch to list B after reaching the end. Similarly, let p2 travel list B, then switch to list A. In this way, it is as if the two lists are joined together.
By doing this, p1 and p2 will enter the common part at the same time, and reach the intersection node c1 together:
You might ask: what if the two lists do not intersect? Can this method return null correctly?
Yes, this logic works. If there is no intersection, the c1 node is null, and the algorithm will return null.
With this idea, we can write the code as follows:
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
// p1 points to the head of list A, p2 points to the head of list B
ListNode p1 = headA, p2 = headB;
while (p1 != p2) {
// p1 takes one step forward, if it reaches the end of list A, switch to list B
if (p1 == null) p1 = headB;
else p1 = p1.next;
// p2 takes one step forward, if it reaches the end of list B, switch to list A
if (p2 == null) p2 = headA;
else p2 = p2.next;
}
return p1;
}
}class Solution {
public:
ListNode* getIntersectionNode(ListNode* headA, ListNode* headB) {
// p1 points to the head of list A, p2 points to the head of list B
ListNode* p1 = headA;
ListNode* p2 = headB;
while (p1 != p2) {
// p1 takes one step forward, if it reaches the end of list A, switch to list B
p1 = (p1 == nullptr) ? headB : p1->next;
// p2 takes one step forward, if it reaches the end of list B, switch to list A
p2 = (p2 == nullptr) ? headA : p2->next;
}
return p1;
}
};class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
# p1 points to the head of list A, p2 points to the head of list B
p1, p2 = headA, headB
while p1 != p2:
# p1 takes one step forward, if it reaches the end of list A, switch to list B
p1 = headB if p1 is None else p1.next
# p2 takes one step forward, if it reaches the end of list B, switch to list A
p2 = headA if p2 is None else p2.next
return p1func getIntersectionNode(headA, headB *ListNode) *ListNode {
// p1 points to the head of list A, p2 points to the head of list B
p1, p2 := headA, headB
for p1 != p2 {
// p1 takes one step forward, if it reaches the end of list A, switch to list B
if p1 == nil {
p1 = headB
} else {
p1 = p1.Next
}
// p2 takes one step forward, if it reaches the end of list B, switch to list A
if p2 == nil {
p2 = headA
} else {
p2 = p2.Next
}
}
return p1
}var getIntersectionNode = function(headA, headB) {
// p1 points to the head of list A, p2 points to the head of list B
let p1 = headA, p2 = headB;
while (p1 !== p2) {
// p1 takes one step forward, if it reaches the end of list A, switch to list B
if (p1 === null) p1 = headB;
else p1 = p1.next;
// p2 takes one step forward, if it reaches the end of list B, switch to list A
if (p2 === null) p2 = headA;
else p2 = p2.next;
}
return p1;
};Open the visualization panel below, and click on the line while (p1 !== p2) several times. You can see how the two pointers meet at the intersection.
Algorithm Visualization
In this way, the problem is solved. The space complexity is and the time complexity is .
These are all the tips for singly linked lists. I hope they inspire you.
Update 2022/1/24:
Some great readers left other solutions in the comments for "Finding the intersection node of two linked lists". I will share them here.
First, some readers noticed that if you connect the two lists end to end, the problem becomes the "Find the start of a cycle" problem discussed before:
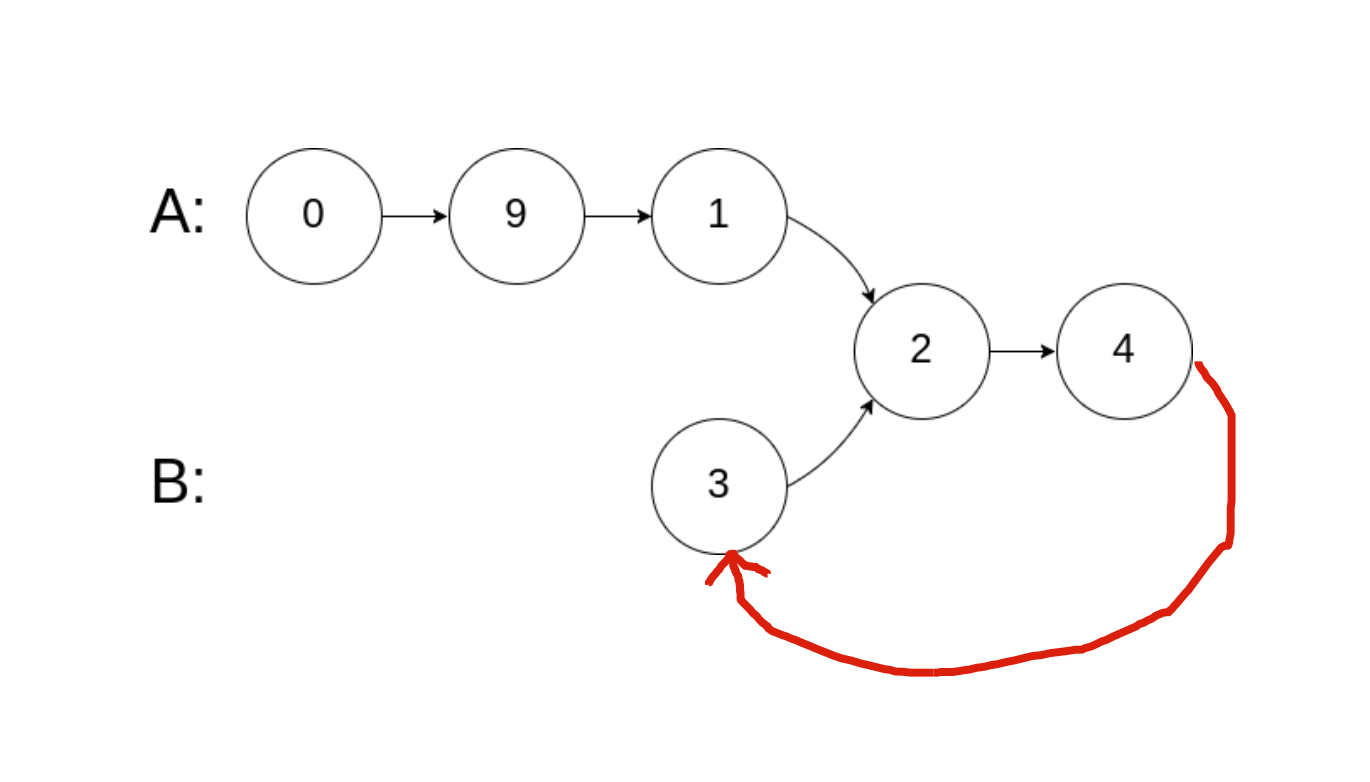
To be honest, I did not think of this approach. It is a clever trick! But keep in mind, this question says you cannot change the original structure of the linked lists. So if you turn the input lists into a cycle to solve it, you must change them back after, or your solution will not pass.
Also, some readers said that since the core is to make p1 and p2 reach the intersection node c1 at the same time, you can do this by first calculating the lengths of both lists. Here is the code:
class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
int lenA = 0, lenB = 0;
// calculate the lengths of the two linked lists
for (ListNode p1 = headA; p1 != null; p1 = p1.next) {
lenA++;
}
for (ListNode p2 = headB; p2 != null; p2 = p2.next) {
lenB++;
}
// make p1 and p2 the same distance from the end
ListNode p1 = headA, p2 = headB;
if (lenA > lenB) {
for (int i = 0; i < lenA - lenB; i++) {
p1 = p1.next;
}
} else {
for (int i = 0; i < lenB - lenA; i++) {
p2 = p2.next;
}
}
// check if the two pointers become the same, when p1 == p2, there are two scenarios:
// 1. either the two linked lists do not intersect,
// they both move to the end null pointer
// 2. or the two linked lists intersect, they reach the
// intersection point of the two linked lists
while (p1 != p2) {
p1 = p1.next;
p2 = p2.next;
}
return p1;
}
}class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
int lenA = 0, lenB = 0;
// calculate the lengths of the two linked lists
for (ListNode* p1 = headA; p1 != nullptr; p1 = p1->next) {
lenA++;
}
for (ListNode* p2 = headB; p2 != nullptr; p2 = p2->next) {
lenB++;
}
// make the distance to the end equal for p1 and p2
ListNode* p1 = headA;
ListNode* p2 = headB;
if (lenA > lenB) {
for (int i = 0; i < lenA - lenB; i++) {
p1 = p1->next;
}
} else {
for (int i = 0; i < lenB - lenA; i++) {
p2 = p2->next;
}
}
// check if the two pointers are the same, there are two cases when p1 == p2:
// 1. either the two linked lists do not intersect,
// and they both reach the end null pointer
// 2. or the two linked lists intersect, and they reach
// the intersection point of the two linked lists
while (p1 != p2) {
p1 = p1->next;
p2 = p2->next;
}
return p1;
}
};class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
lenA, lenB = 0, 0
# calculate the length of both linked lists
p1, p2 = headA, headB
while p1:
lenA += 1
p1 = p1.next
while p2:
lenB += 1
p2 = p2.next
# make p1 and p2 reach the same distance from the end
p1, p2 = headA, headB
if lenA > lenB:
for _ in range(lenA - lenB):
p1 = p1.next
else:
for _ in range(lenB - lenA):
p2 = p2.next
# check if the two pointers are the same, there are two cases when p1 == p2:
# 1. either the two linked lists do not intersect and both reach the end null pointer
# 2. or the two linked lists intersect and they reach the intersection point
while p1 != p2:
p1 = p1.next
p2 = p2.next
return p1func getIntersectionNode(headA, headB *ListNode) *ListNode {
lenA, lenB := 0, 0
// calculate the lengths of the two linked lists
for p1 := headA; p1 != nil; p1 = p1.Next {
lenA++
}
for p2 := headB; p2 != nil; p2 = p2.Next {
lenB++
}
// make p1 and p2 reach the same distance from the end
p1, p2 := headA, headB
if lenA > lenB {
for i := 0; i < lenA - lenB; i++ {
p1 = p1.Next
}
} else {
for i := 0; i < lenB - lenA; i++ {
p2 = p2.Next
}
}
// see if the two pointers will be the same, when p1 == p2 there are two cases:
// 1. either the two linked lists do not intersect, and
// they simultaneously reach the null pointer at the end
// 2. or the two linked lists intersect, and they reach
// the intersection point of the two linked lists
for p1 != p2 {
p1 = p1.Next
p2 = p2.Next
}
return p1
}var getIntersectionNode = function(headA, headB) {
let lenA = 0, lenB = 0;
// calculate the lengths of the two linked lists
for (let p1 = headA; p1 != null; p1 = p1.next) {
lenA++;
}
for (let p2 = headB; p2 != null; p2 = p2.next) {
lenB++;
}
// make p1 and p2 have the same distance to the end
let p1 = headA, p2 = headB;
if (lenA > lenB) {
for (let i = 0; i < lenA - lenB; i++) {
p1 = p1.next;
}
} else {
for (let i = 0; i < lenB - lenA; i++) {
p2 = p2.next;
}
}
// check if the two pointers become the same, there are two cases when p1 == p2:
// 1. either the two linked lists do not intersect,
// and they both reach the null pointer at the end
// 2. or the two linked lists intersect, and they reach the intersection point
while (p1 != p2) {
p1 = p1.next;
p2 = p2.next;
}
return p1;
};Though this code is a bit longer, the time complexity is still , and it may be easier to understand.
In short, my solution may not be the best or the only correct one. I encourage everyone to post your questions and thoughts in the comments. I am also happy to discuss more problem-solving ideas with you!
Now, you have learned all the two-pointer tricks for linked lists. For more practice, see More Classic Linked List Two-Pointer Problems.