Time and Space Complexity Analysis Practical Guide

My previous articles primarily focused on explaining algorithm principles and problem-solving thinking, often glossing over the analysis of time and space complexity for the following reasons:

1. For beginner readers, I want you to concentrate on understanding the principles of algorithms. Adding too much mathematical content can easily discourage readers.

2. A correct understanding of the underlying principles of common algorithms is a prerequisite for analyzing complexity. Especially for recursion-related algorithms, only by thinking and analyzing from a tree perspective can you correctly analyze their complexity.

Since historical articles now cover the core principles of all common algorithms, I have specifically written a guide on time and space complexity analysis. Instead of giving you a fish, it is better to teach you how to fish by providing a general method to analyze the time and space complexity of any algorithm.

This article will be lengthy and cover the following points:

1. Using time complexity to deduce problem-solving approaches, reducing trial and error.

2. Where does the time go? Common coding mistakes that lead to algorithm timeouts.

3. Basic characteristics of Big O notation.

4. Analysis of time complexity in non-recursive algorithms.

5. Efficiency measurement methods of data structure APIs (amortized analysis).

6. Analysis methods for time/space complexity of recursive algorithms, with a focus on this area, using dynamic programming and backtracking algorithms as examples.

Before explaining the concept of complexity and specific calculation methods, I will discuss some common techniques and pitfalls encountered in practice.

Use Time Complexity to Decide How to Solve Problems

For example, if a problem gives you an array with length up to 10^6, you can know the time complexity should be less than $O(N^2)$. You need to make your code $O(NlogN)$ or $O(N)$. If your algorithm is $O(N^2)$, the total operations can reach 10^12, which is too much for most online judges.

To keep the complexity at $O(NlogN)$ or $O(N)$, you can choose from sorting, prefix sum, two pointers, 1D dynamic programming, and similar ideas. Approaches like nested for loops, 2D DP, or backtracking can be ruled out.

Another example, if the problem gives a very small data size, like array length N not more than 20, then you can guess that the problem wants you to use brute-force.

Online judges usually give large data to make things hard. If the data is very small, it means the best solution is probably exponential or factorial time. You can safely use backtracking for these cases.

Many people ignore the data size and start coding right away. This is not a good habit. You should always consider all information in the problem before you start coding. This way, you avoid going down the wrong path.

Coding Mistakes That Cause Time Complexity Problems

This part summarizes some common mistakes (especially for beginners) that can make your code slower than expected, or even cause timeouts.

Using Standard Output

When solving algorithm problems, you might use print or console.log to debug your code.

Before submitting your code, remember to remove or comment out these output statements. Standard output is an I/O operation and can slow down your algorithm a lot.

Passing by Value Instead of by Reference

In C++, function parameters are passed by value by default. For example, if you pass a vector to a function, the whole data structure will be copied, causing extra time and memory usage. If this happens in a recursive function, it will almost always cause a timeout or run out of memory.

The correct way is to pass by reference, like vector<int>&. If you use other languages, check how parameters are passed. Make sure you understand this in your language.

Not Knowing the Implementation of Interface Objects

This problem is more common in object-oriented languages like Java, but it still needs attention.

In Java, List is an interface. It has many implementations, such as ArrayList and LinkedList. If you have learned how to implement dynamic arrays and linked lists, you know that many methods have different complexities. For example, ArrayList's get method is $O(1)$, but LinkedList's get method is $O(N)$.

If a function parameter is given as List, would you dare to use list.get(i) for random access? Probably not.

In these cases, it is safer to create an ArrayList and copy all elements from the input List into it, so you can use index access safely.

These are the main issues. They are not algorithm ideas, but practical problems. Pay attention to them and you should be fine. Next, we will start the main topic of algorithm complexity analysis.

Big O Notation

The symbol O (capital letter o, not the number 0) represents a set of functions. For example, $O(n^2)$ represents a set of functions derived from g(n) = n^2; when we say an algorithm has a time complexity of $O(n^2)$, it means the function describing the complexity of the algorithm belongs to this set.

In theory, understanding this abstract mathematical definition can answer all your questions about Big O notation.

However, considering that most people feel dizzy when they see mathematical definitions, I will list two properties used in complexity analysis. Remembering these two will be enough.

1. Keep only the fastest-growing term; other terms can be omitted.

Firstly, constant factors in multiplication and addition can be ignored, as shown in the following examples:

O(2N + 100) = O(N)
O(2^(N+1)) = O(2 * 2^N) = O(2^N)
O(M + 3N + 99) = O(M + N)

Of course, not every constant can be omitted; some may require using exponential rules learned in school:

O(2^(2N)) = O(4^N)

Besides constant factors, terms with a slower growth rate can also be ignored in the face of terms with a faster growth rate:

O(N^3 + 999 * N^2 + 999 * N) = O(N^3)
O((N + 1) * 2^N) = O(N * 2^N + 2^N) = O(N * 2^N)

These are the simplest and most common examples, and all can be correctly explained by the definition of Big O notation. If you encounter more complex scenarios, you can use the definition to determine if your complexity expression is correct.

2. Big O Notation Shows the "Upper Bound" of Complexity

In other words, as long as you give an upper bound, using Big O notation is correct.

For example, look at this code:

for (int i = 0; i < N; i++) {
    print("hello world");
}

If this is an algorithm, its time complexity is obviously $O(N)$. But if you say the time complexity is $O(N^2)$, this is also correct in theory because Big O shows an upper bound. The time complexity will not be more than $N^2$. Although this upper bound is not tight, it fits the definition. So, in theory, there is nothing wrong.

The example above is simple, and using a loose upper bound does not make much sense. But some algorithms have complexity that depends on the input data, so sometimes you cannot give an exact time complexity. In such cases, giving a loose upper bound with Big O is helpful.

For example, in Dynamic Programming Core Framework, the brute-force recursive solution for the coin change problem looks like this:

// Definition: To make up amount n, need at least dp(coins, n) coins
int dp(int[] coins, int amount) {
    // base case
    if (amount <= 0) return;
    // state transition
    for (int coin : coins) {
        dp(coins, amount - coin);
    }
}

When amount = 11, coins = [1,2,5], the recursion tree looks like this:

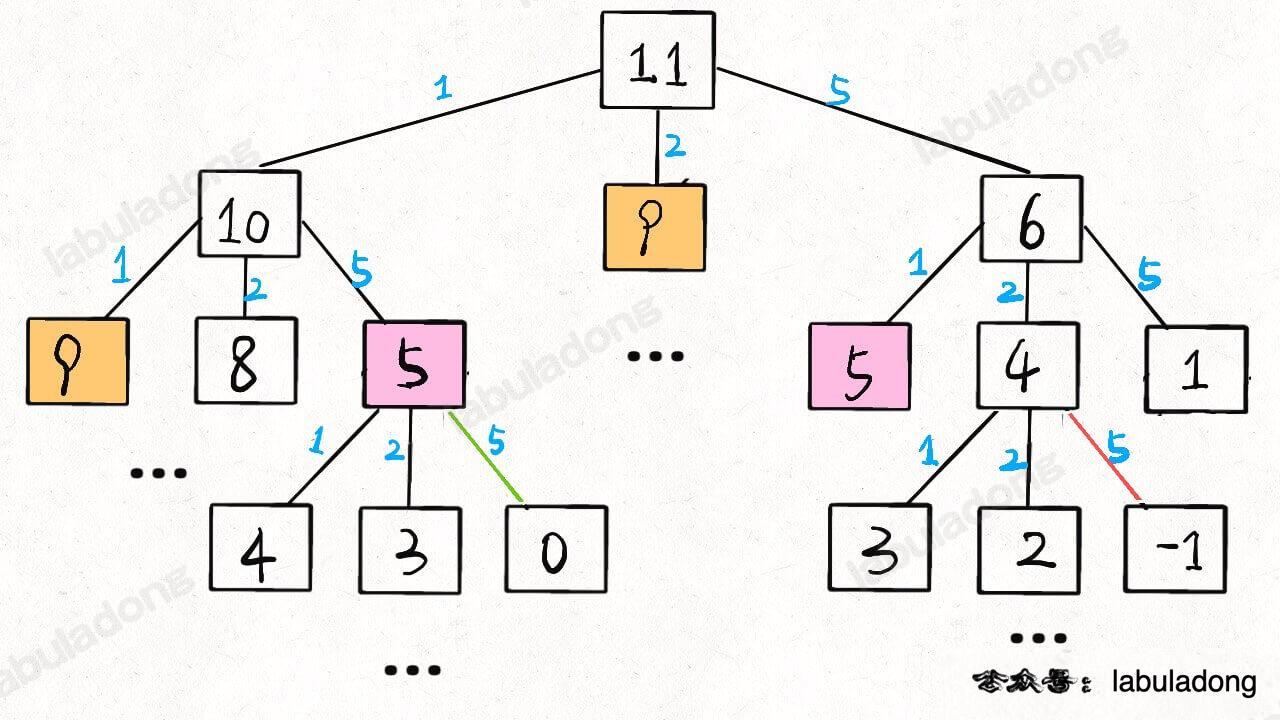
We will talk later about how to calculate the time complexity of recursive algorithms. For now, let's just count the number of nodes in this recursion tree.

Suppose the value of amount is N, and there are K coins in the list. This recursion tree is a K-ary tree. But the structure depends on the coin values, so the tree is not regular, and it is hard to count the exact number of nodes.

In this case, the easy way is to use the worst case:

How tall can this tree be? We don't know, so let's say the worst case is all coins are of value 1. In this case, the height is N.

What is the structure of the tree? We don't know, so let's use the worst case again and say it is a full K-ary tree.

So, how many nodes does this tree have? In the worst case, a full K-ary tree of height N has (K^N - 1)/(K - 1) nodes. In Big O, this is $O(K^N)$.

Of course, we know the actual number of nodes is less than this, but using $O(K^N)$ as a rough upper bound is fine. It is also clear that this is an exponential algorithm, so we need to optimize it.

So, if the time complexity estimate you get is different from someone else’s, it does not mean one of you is wrong. Both can be right, just at different levels of accuracy.

In theory, we want a tight upper bound, but getting it needs good math skills. For real interview problems, just knowing the order of growth (linear, exponential, logarithmic, quadratic, etc.) is enough.

In algorithms, besides Big O for upper bound, there are also notations for lower bound and tight bound. You can look them up if interested. But for practical use, what we discussed about Big O is enough.

Analysis of Non-Recursive Algorithms

For non-recursive algorithms, space complexity is usually easy to find. Just check if it uses arrays or other storage. So, I will focus on time complexity analysis.

Data Structure Analysis

Recursive Algorithm Analysis

Final Summary