Thinking Recursion Algorithms from Binary Tree Perspective
This article will resolve
| LeetCode | Difficulty |
|---|---|
| 104. Maximum Depth of Binary Tree | 🟢 |
| 144. Binary Tree Preorder Traversal | 🟢 |
| 543. Diameter of Binary Tree | 🟢 |
Prerequisites
Before reading this article, you need to learn:
How to Read This Article
This article summarizes and abstracts many algorithms, so there will be many links to other articles.
If this is your first time reading, do not try to read every detail at once. If you see an algorithm you don't know or something you don't understand, just skip it. Just try to get a general idea of the main theories in this article. When you learn more algorithm techniques on this site, you will start to understand the key ideas here. If you come back and read this article again in the future, you will gain more insight.
All articles on this site follow the framework from How to Learn Data Structures and Algorithms. This framework highlights the importance of binary tree problems, which is why this article is in the must-read section of the first chapter.
After years of solving problems, I have summarized all my experience with binary tree algorithms here. My words may not be very academic, and you won't find these summaries in textbooks. But up to now, there is no binary tree problem on any coding platform that is outside the framework I give here. If you find a problem that does not fit this framework, please leave a comment and tell me.
To summarize, there are two main ways to think about solving binary tree problems:
1. Can you solve the problem by traversing the tree once?
If yes, use a traverse function with external variables. This is called the "traversal" thinking pattern.
2. Can you define a recursive function, where the answer to the problem can be built from the answers of its subproblems (subtrees)?
If yes, write this recursive function and use its return value. This is called the "divide the problem" thinking pattern.
No matter which pattern you use, you should ask yourself:
If you take out a single binary tree node, what should it do? When should it do it (preorder, inorder, postorder)?
You don't need to worry about other nodes—the recursive function will make sure the same operation happens on every node.
I will use simple problems as examples in this article, so don't worry if you think you can't understand. I will help you see the common ideas in all binary tree problems, even in the simplest cases. Later, these binary tree ideas can be used for Dynamic Programming, Backtracking, Divide and Conquer, and Graph Algorithms. This is why I always stress the importance of thinking in frameworks. I hope after learning those advanced algorithms, you can come back and read this article again and get a deeper understanding.
Let me repeat once more how important the binary tree structure and related algorithms are.
The Importance of Binary Trees
For example, take two famous sorting algorithms: Quicksort and Mergesort. What do you know about them?
If you tell me that quicksort is just the preorder traversal of a binary tree, and mergesort is the postorder traversal, then I know you really understand algorithms.
Why are quicksort and mergesort related to binary trees? Let's look at how their logic and code frameworks work:
Quicksort: If you want to sort nums[lo..hi], you first find a partition point p. Swap elements so that nums[lo..p-1] are all less than or equal to nums[p], and nums[p+1..hi] are all greater than nums[p]. Then, recursively sort nums[lo..p-1] and nums[p+1..hi]. In the end, the array is sorted.
Here is the framework for quicksort:
void sort(int[] nums, int lo, int hi) {
if (lo >= hi) {
return;
}
// ****** pre-order position ******
// partition the nums[lo..hi], put nums[p] in the right position
// such that nums[lo..p-1] <= nums[p] < nums[p+1..hi]
int p = partition(nums, lo, hi);
// recursively partition the left and right subarrays
sort(nums, lo, p - 1);
sort(nums, p + 1, hi);
}void sort(int nums[], int lo, int hi) {
if (lo >= hi) {
return;
}
// ****** pre-order position ******
// partition the nums[lo..hi], put nums[p] in the right position
// such that nums[lo..p-1] <= nums[p] < nums[p+1..hi]
int p = partition(nums, lo, hi);
// recursively partition the left and right subarrays
sort(nums, lo, p - 1);
sort(nums, p + 1, hi);
}def sort(nums: List[int], lo: int, hi: int):
if lo >= hi:
return
# ****** pre-order position ******
# partition the nums[lo..hi], put nums[p] in the right position
# such that nums[lo..p-1] <= nums[p] < nums[p+1..hi]
p = partition(nums, lo, hi)
# recursively partition the left and right subarrays
sort(nums, lo, p - 1)
sort(nums, p + 1, hi)func sort(nums []int, lo int, hi int) {
if lo >= hi {
return
}
// ****** pre-order position ******
// partition the nums[lo..hi], put nums[p] in the right position
// such that nums[lo..p-1] <= nums[p] < nums[p+1..hi]
p := partition(nums, lo, hi)
// recursively partition the left and right subarrays
sort(nums, lo, p-1)
sort(nums, p+1, hi)
}var sort = function(nums, lo, hi) {
if (lo >= hi) {
return;
}
// ****** pre-order position ******
// partition the nums[lo..hi], put nums[p] in the right position
// make nums[lo..p-1] <= nums[p] < nums[p+1..hi]
var p = partition(nums, lo, hi);
// recursively partition the left and right subarrays
sort(nums, lo, p - 1);
sort(nums, p + 1, hi);
};First, build the partition point, then solve the left and right subarrays. Isn't this just a preorder traversal of a binary tree?
Now, mergesort: If you want to sort nums[lo..hi], first sort nums[lo..mid], then sort nums[mid+1..hi], and finally merge the two sorted subarrays. The array is then sorted.
Here is the framework for mergesort:
// definition: sort nums[lo..hi]
void sort(int[] nums, int lo, int hi) {
if (lo == hi) {
return;
}
int mid = (lo + hi) / 2;
// use the definition to sort nums[lo..mid]
sort(nums, lo, mid);
// use the definition to sort nums[mid+1..hi]
sort(nums, mid + 1, hi);
// ****** Post-order position ******
// at this point, the two subarrays are already sorted
// merge the two sorted arrays to make nums[lo..hi] sorted
merge(nums, lo, mid, hi);
}// definition: sort nums[lo..hi]
void sort(int[] nums, int lo, int hi) {
if (lo == hi) {
return;
}
int mid = (lo + hi) / 2;
// use the definition to sort nums[lo..mid]
sort(nums, lo, mid);
// use the definition to sort nums[mid+1..hi]
sort(nums, mid + 1, hi);
// ****** Post-order position ******
// at this point, the two subarrays are already sorted
// merge the two sorted arrays to make nums[lo..hi] sorted
merge(nums, lo, mid, hi);
}# definition: sort the array nums[lo..hi]
def sort(nums: List[int], lo: int, hi: int) -> None:
if lo == hi:
return
mid = (lo + hi) // 2
# Using the definition, sort the array nums[lo..mid]
sort(nums, lo, mid)
# Using the definition, sort the array nums[mid+1..hi]
sort(nums, mid + 1, hi)
# ****** Post-order position ******
# At this point, the two subarrays have been sorted
# Merge the two sorted arrays to make nums[lo..hi] sorted
merge(nums, lo, mid, hi)// definition: sort the nums[lo..hi]
func sort(nums []int, lo, hi int) {
if lo == hi {
return
}
mid := (lo + hi) / 2
// use the definition to sort nums[lo..mid]
sort(nums, lo, mid)
// use the definition to sort nums[mid+1..hi]
sort(nums, mid+1, hi)
// ****** Post-order position ******
// at this point, the two subarrays are already sorted
// merge two sorted arrays to make nums[lo..hi] sorted
merge(nums, lo, mid, hi)
}// definition: sort the array nums[lo..hi]
function sort(nums, lo, hi) {
if (lo == hi) {
return;
}
var mid = Math.floor((lo + hi) / 2);
// utilize the definition, sort nums[lo..mid]
sort(nums, lo, mid);
// utilize the definition, sort nums[mid+1..hi]
sort(nums, mid + 1, hi);
// ****** Post-order position ******
// at this point, the two subarrays have been sorted
// merge two sorted arrays to make nums[lo..hi] sorted
merge(nums, lo, mid, hi);
}First sort the left and right subarrays, then merge them (similar to merging two sorted linked lists). This is the postorder traversal of a binary tree. Also, this is what we call divide and conquer — that's all.
If you can see the binary tree pattern in these sorting algorithms, you do not need to memorize them. You can easily write them yourself by extending the binary tree traversal framework.
All of this shows that binary tree algorithm ideas are widely used. In fact, if a problem uses recursion, it can often be seen as a binary tree problem.
Next, let's start with preorder, inorder, and postorder traversals, so you can clearly see the beauty of this data structure.
Understand Preorder, Inorder, and Postorder Traversal
Let me give you a few questions. Think about them for 30 seconds:
What do you think preorder, inorder, and postorder traversals of a binary tree are? Are they just three lists in different orders?
Can you explain what is special about postorder traversal?
Why does an n-ary tree (a tree with more than two children per node) not have an inorder traversal?
If you cannot answer these, it means you only know the textbook understanding of these traversals. Don't worry, I will use simple comparisons to explain how I see these traversals.
First, let's review the binary tree recursive traversal framework mentioned in Binary Tree DFS/BFS Traversal:
// Binary tree traversal framework
void traverse(TreeNode root) {
if (root == null) {
return;
}
// pre-order position
traverse(root.left);
// in-order position
traverse(root.right);
// post-order position
}// binary tree traversal framework
void traverse(TreeNode* root) {
if (root == nullptr) {
return;
}
// pre-order position
traverse(root->left);
// in-order position
traverse(root->right);
// post-order position
}# Binary tree traversal framework
def traverse(root):
if root is None:
return
# Pre-order position
traverse(root.left)
# In-order position
traverse(root.right)
# Post-order position// Binary tree traversal framework
func traverse(root *TreeNode) {
if root == nil {
return
}
// Preorder position
traverse(root.Left)
// Inorder position
traverse(root.Right)
// Postorder position
}// binary tree traversal framework
var traverse = function(root) {
if (root === null) {
return;
}
// pre-order position
traverse(root.left);
// in-order position
traverse(root.right);
// post-order position
};Ignore the terms preorder, inorder, and postorder for now. Look at the traverse function. What is it really doing?
It is simply a function that visits every node in the binary tree. This is just like traversing an array or a linked list.
// iterate through the array
void traverse(int[] arr) {
for (int i = 0; i < arr.length; i++) {
}
}
// recursively traverse the array
void traverse(int[] arr, int i) {
if (i == arr.length) {
return;
}
// pre-order position
traverse(arr, i + 1);
// post-order position
}
// iterate through the singly linked list
void traverse(ListNode head) {
for (ListNode p = head; p != null; p = p.next) {
}
}
// recursively traverse the singly linked list
void traverse(ListNode head) {
if (head == null) {
return;
}
// pre-order position
traverse(head.next);
// post-order position
}// iterative traversal of the array
void traverse(vector<int>& arr) {
for (int i = 0; i < arr.size(); i++) {
}
}
// recursive traversal of the array
void traverse(vector<int>& arr, int i) {
if (i == arr.size()) {
return;
}
// pre-order position
traverse(arr, i + 1);
// post-order position
}
// iterative traversal of the singly linked list
void traverse(ListNode* head) {
for (ListNode* p = head; p != nullptr; p = p->next) {
}
}
// recursive traversal of the singly linked list
void traverse(ListNode* head) {
if (head == nullptr) {
return;
}
// pre-order position
traverse(head->next);
// post-order position
}# iterate through the array
def traverse(arr: List[int]) -> None:
for i in range(len(arr)):
pass
# recursively traverse the array
def traverse_recursive(arr: List[int], i: int) -> None:
if i == len(arr):
return
# pre-order position
traverse_recursive(arr, i + 1)
# post-order position
# iterate through the singly linked list
def traverse_linked_list(head: ListNode) -> None:
p = head
while p:
p = p.next
# recursively traverse the singly linked list
def traverse_linked_list_recursive(head: ListNode) -> None:
if not head:
return
# pre-order position
traverse_linked_list_recursive(head.next)
# post-order position// iterate through the array
func traverse(arr []int) {
for i := 0; i < len(arr); i++ {
}
}
// recursively traverse the array
func traverse(arr []int, i int) {
if i == len(arr) {
return;
}
// pre-order position
traverse(arr, i + 1)
// post-order position
}
// iterate through the singly linked list
func traverse(head *ListNode) {
for p := head; p != nil; p = p.Next {
}
}
// recursively traverse the singly linked list
func traverse(head *ListNode) {
if head == nil {
return;
}
// pre-order position
traverse(head.Next)
// post-order position
}// iterate through the array
var traverse = function(arr) {
for (var i = 0; i < arr.length; i++) {
}
}
// recursively traverse the array
var traverseRecursive = function(arr, i) {
if (i == arr.length) {
return;
}
// pre-order position
traverseRecursive(arr, i + 1);
// post-order position
}
// iterate through the singly linked list
var traverseList = function(head) {
for (var p = head; p != null; p = p.next) {
}
}
// recursively traverse the singly linked list
var traverseListRecursive = function(head) {
if (head == null) {
return;
}
// pre-order position
traverseListRecursive(head.next);
// post-order position
}You can traverse a singly linked list or an array by iteration or recursion. A binary tree is just a type of linked structure, but it cannot be easily rewritten as a for loop. So we usually use recursion to traverse a binary tree.
You may also have noticed that recursive traversals can have a "preorder position" and a "postorder position". Preorder is before the recursion, postorder is after the recursion.
Preorder position is when you just enter a node. Postorder position is when you are about to leave a node. If you put code in different positions, it will run at different times:
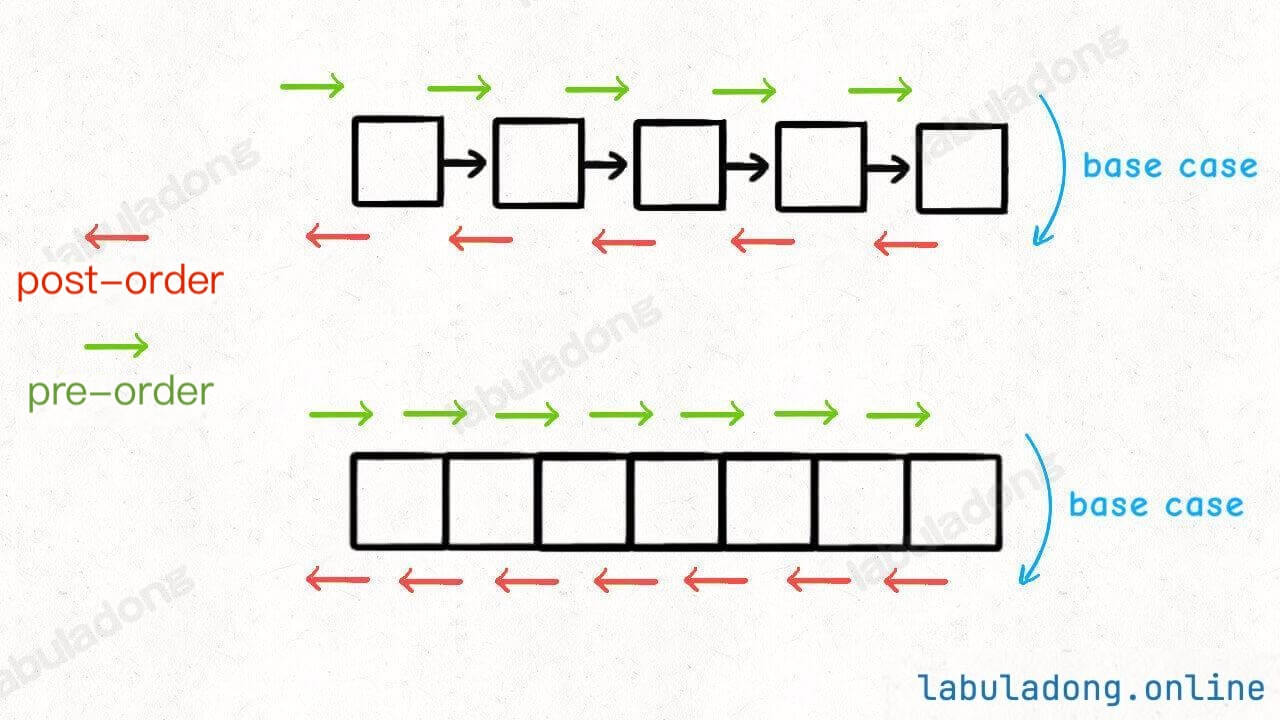
For example, if you want to print the values of a singly linked list in reverse order, how would you do it?
There are many ways, but if you understand recursion well, you can use the postorder position:
// recursively traverse a singly linked list and print the elements in reverse order
void traverse(ListNode head) {
if (head == null) {
return;
}
traverse(head.next);
// post-order position
print(head.val);
}// recursively traverse the singly linked list and print elements in reverse order
void traverse(ListNode* head) {
if (head == nullptr) {
return;
}
traverse(head->next);
// post-order position
cout << head->val << endl;
}# recursively traverse a singly linked list and print the elements in reverse order
def traverse(head):
if head is None:
return
traverse(head.next)
# post-order position
print(head.val)// recursively traverse the singly linked list and print the elements in reverse order
func traverse(head *ListNode) {
if head == nil {
return
}
traverse(head.Next)
// post-order position
fmt.Println(head.Val)
}// Recursively traverse the singly linked list and print the elements in reverse order
var traverse = function(head) {
if (head == null) {
return;
}
traverse(head.next);
// postorder position
console.log(head.val);
};With the picture above, you can see why this code prints the linked list in reverse order. It uses the call stack from recursion to print from the end to the start.
The same idea applies to binary trees, but there is also an "inorder position".
Textbooks often ask you to list the results of preorder, inorder, and postorder traversals. So, many people think these are just three lists in different orders.
But I want to say, preorder, inorder, and postorder are actually three special moments when you process each node during tree traversal, not just three lists.
- Preorder position: code runs when you just enter a binary tree node.
- Postorder position: code runs when you are about to leave a binary tree node.
- Inorder position: code runs when you have finished visiting the left subtree and are about to visit the right subtree of a node.
Notice that I always say "preorder/inorder/postorder position" instead of "traversal". This is to show the difference: you can put code at the preorder position to add elements to a list, and you will get the preorder traversal result. But you can also write more complex code to do other things.
Here is a picture of the three positions on a binary tree:
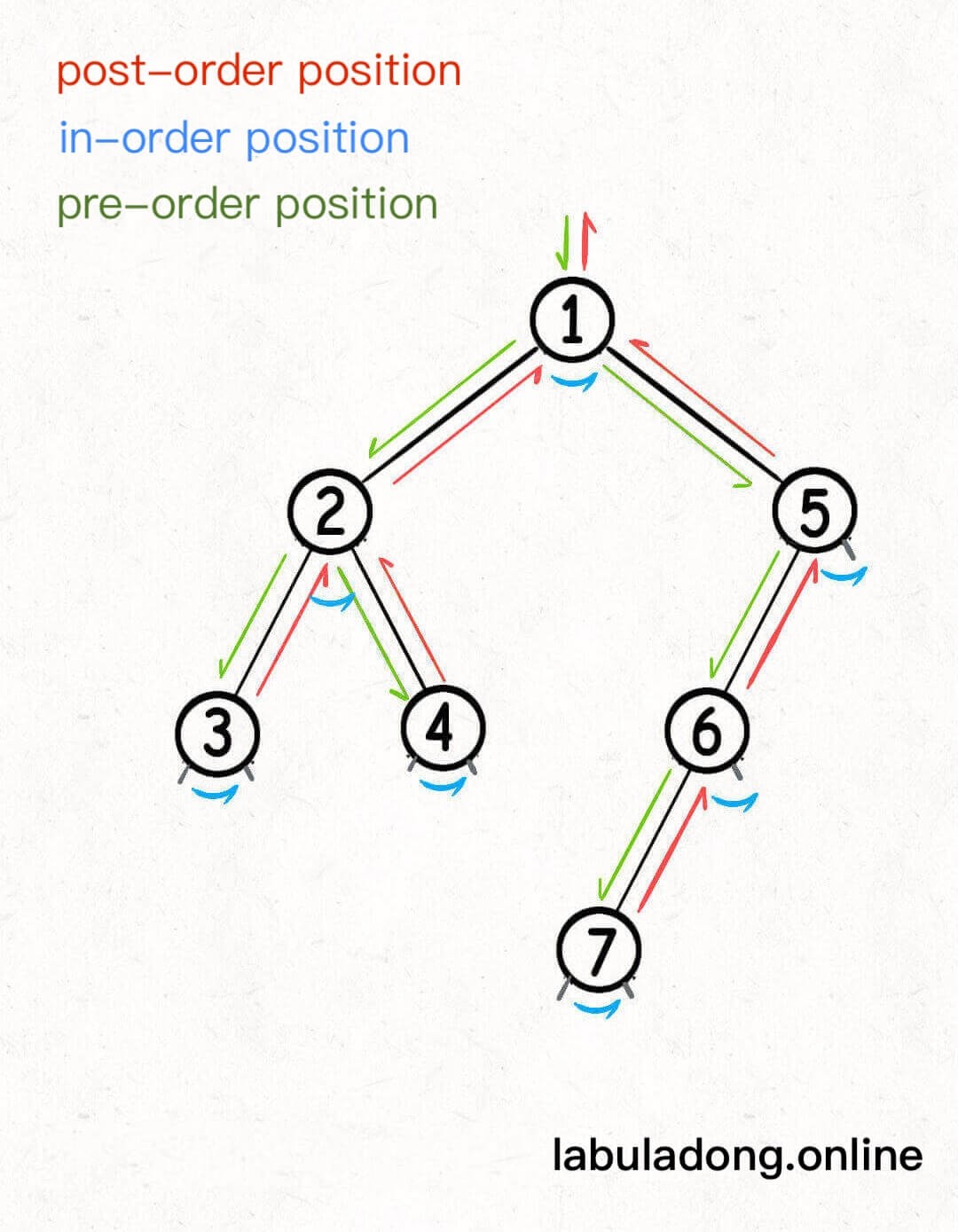
You can see that every node has its own unique preorder, inorder, and postorder position. So, preorder/inorder/postorder are three special times to process each node during traversal.
Now you can also understand why an n-ary tree does not have an inorder position. In a binary tree, each node switches from left to right subtree only once, so there is a unique inorder position. But in an n-ary tree, a node can have many children and switch between them many times, so there is no unique inorder position.
All of this is to help you build the right understanding of binary trees. You will see:
All binary tree problems can be solved by writing smart logic at preorder, inorder, or postorder positions. You only need to think about what to do with each node. The traversal framework and recursion will handle the rest and apply your code to all nodes.
You can also see in Graph Algorithm Basics that the binary tree traversal framework can be extended to graphs, and many classic graph algorithms are built on traversal. But that's a topic for another article.
Two Approaches to Solving Problems
In the previous article My Algorithm Learning Insights, it was mentioned:
There are two approaches to solving binary tree problems using recursion. The first is to traverse the binary tree once to get the answer, and the second is to decompose the problem to calculate the answer. These two approaches correspond to the Backtracking Core Framework and Dynamic Programming Core Framework, respectively.
Tip
Here I will mention my function naming convention: when solving problems in a binary tree using a traversal approach, the function signature is generally void traverse(...), with no return value, relying on updating external variables to compute results. When solving problems using a decomposition approach, the function name depends on its specific function and usually has a return value, which is the result of the sub-problem's computation.
Correspondingly, you will find that in the Backtracking Core Framework, the given function signatures usually have no return value, void backtrack(...), while in the Dynamic Programming Core Framework, the function signatures have return values, dp functions. This illustrates the intricate connections between them and binary trees.
Although there are no strict requirements for function naming, I suggest following this style to better highlight the function's purpose and problem-solving mindset, making it easier for you to understand and apply.
At the time, I used the problem of finding the maximum depth of a binary tree as an example, focusing on comparing these two approaches with dynamic programming and backtracking algorithms. The focus of this article is on analyzing how these two approaches solve binary tree problems.
LeetCode Problem 104: Maximum Depth of Binary Tree is about finding the maximum depth. The maximum depth is the number of nodes along the longest path from the root node to the "furthest" leaf node. For example, given this binary tree, the algorithm should return 3:
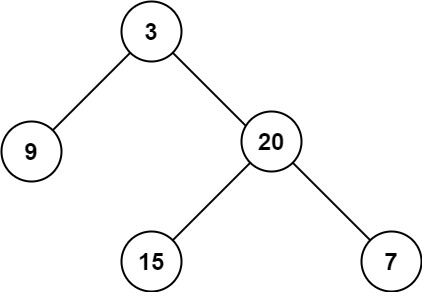
What is your approach to solving this problem? Clearly, by traversing the binary tree once and using an external variable to record the depth of each node, taking the maximum value can yield the maximum depth. This is the approach of traversing the binary tree to calculate the answer.
The solution code is as follows:
// Traversal Idea
class Solution {
// Record the depth of the traversed node
int depth = 0;
// Record the maximum depth
int res = 0;
public int maxDepth(TreeNode root) {
traverse(root);
return res;
}
// Traverse the binary tree
void traverse(TreeNode root) {
if (root == null) {
return;
}
// Pre-order traversal position (entering a node) increases depth
depth++;
// Record the maximum depth during traversal
if (root.left == null && root.right == null) {
res = Math.max(res, depth);
}
traverse(root.left);
traverse(root.right);
// Post-order traversal position (leaving a node) decreases depth
depth--;
}
}// Traversal Idea
class Solution {
// record the maximum depth
int res = 0;
// record the depth of the traversed node
int depth = 0;
public:
int maxDepth(TreeNode* root) {
traverse(root);
return res;
}
// Traverse the binary tree
void traverse(TreeNode* root) {
if (root == nullptr) {
return;
}
// Pre-order traversal position (entering a node) increases depth
depth++;
// Record the maximum depth during traversal
if (root->left == nullptr && root->right == nullptr) {
res = std::max(res, depth);
}
traverse(root->left);
traverse(root->right);
// Post-order traversal position (leaving a node) decreases depth
depth--;
}
};# Traversal Idea
class Solution:
def __init__(self):
# Record the depth of the traversed node
self.depth = 0
# Record the maximum depth
self.res = 0
def maxDepth(self, root: TreeNode) -> int:
self.traverse(root)
return self.res
# Traverse the binary tree
def traverse(self, root: TreeNode):
if root is None:
return
# Pre-order traversal position (entering a node) increases depth
self.depth += 1
# Record the maximum depth during traversal
if root.left is None and root.right is None:
self.res = max(self.res, self.depth)
self.traverse(root.left)
self.traverse(root.right)
# Post-order traversal position (leaving a node) decreases depth
self.depth -= 1func maxDepth(root *TreeNode) int {
// Record the depth of the traversed node
depth := 0
// Record the maximum depth
res := 0
traverse(root, &depth, &res)
return res
}
// Traverse the binary tree
func traverse(root *TreeNode, depth *int, res *int) {
if root == nil {
return
}
// Pre-order traversal position (entering a node) increases depth
*depth++
// Record the maximum depth during traversal
if root.Left == nil && root.Right == nil {
*res = max(*res, *depth)
}
traverse(root.Left, depth, res)
traverse(root.Right, depth, res)
// Post-order traversal position (leaving a node) decreases depth
*depth--
}
// Traversal Idea
func max(a, b int) int {
if a > b {
return a
}
return b
}// Traversal Idea
var maxDepth = function(root) {
// Record the depth of the traversed node
let depth = 0;
// Record the maximum depth
let res = 0;
// Traverse the binary tree
var traverse = function(node) {
if (node === null) {
return;
}
// Pre-order traversal position (entering a node) increases depth
depth++;
// Record the maximum depth during traversal
if (node.left === null && node.right === null) {
res = Math.max(res, depth);
}
traverse(node.left);
traverse(node.right);
// Post-order traversal position (leaving a node) decreases depth
depth--;
};
traverse(root);
return res;
};Visualization of the Traversal Approach
This solution should be easy to understand, but why do we need to increase depth at the pre-order position and decrease it at the post-order position?
As mentioned earlier, the pre-order position is when entering a node, and the post-order position is when leaving a node. The depth records the depth of the current recursive node. You can think of traverse as a pointer moving through the binary tree, so it is maintained this way.
As for updating res, you can do it at pre-order, in-order, or post-order positions, as long as it is done after entering the node and before leaving the node (i.e., after incrementing depth and before decrementing it).
Of course, it is also easy to see that the maximum depth of a binary tree can be derived from the maximum depth of its subtrees. This is the idea of decomposing a problem to calculate the answer.
Here is the solution code:
// Divide and Conquer Idea
class Solution {
// Definition: Given a node, return the maximum depth of the binary tree rooted at that node
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
// Use the definition to calculate the maximum depth of the left and right subtrees
int leftMax = maxDepth(root.left);
int rightMax = maxDepth(root.right);
// Derive the maximum depth of the original binary tree based
// on the maximum depth of the left and right subtrees
// The maximum depth of the entire tree is the
// maximum of the left and right subtree depths,
// plus one for the root node itself
return 1 + Math.max(leftMax, rightMax);
}
}// Divide and Conquer Idea
class Solution {
public:
// Definition: Given a node, return the maximum depth of the binary tree rooted at that node
int maxDepth(TreeNode* root) {
if (root == nullptr) {
return 0;
}
// Use the definition to calculate the maximum depth of the left and right subtrees
int leftMax = maxDepth(root->left);
int rightMax = maxDepth(root->right);
// Derive the maximum depth of the original binary tree based
// on the maximum depth of the left and right subtrees
// The maximum depth of the entire tree is the
// maximum of the left and right subtree depths,
// plus one for the root node itself
return 1 + std::max(leftMax, rightMax);
}
};# Divide and Conquer Idea
class Solution:
# Definition: Given a node, return the maximum depth of the binary tree rooted at that node
def maxDepth(self, root: TreeNode) -> int:
if root is None:
return 0
# Use the definition to calculate the maximum depth of the left and right subtrees
leftMax = self.maxDepth(root.left)
rightMax = self.maxDepth(root.right)
# Derive the maximum depth of the original binary tree based
# on the maximum depth of the left and right subtrees
# The maximum depth of the entire tree is the
# maximum of the left and right subtree depths,
# plus one for the root node itself
return 1 + max(leftMax, rightMax)// Divide and Conquer Idea
func maxDepth(root *TreeNode) int {
// Definition: Given a node, return the maximum depth of the binary tree rooted at that node
if root == nil {
return 0
}
// Use the definition to calculate the maximum depth of the left and right subtrees
leftMax := maxDepth(root.Left)
rightMax := maxDepth(root.Right)
// Derive the maximum depth of the original binary tree based
// on the maximum depth of the left and right subtrees
// The maximum depth of the entire tree is the maximum of the left and right subtree depths,
// plus one for the root node itself
return 1 + max(leftMax, rightMax)
}
func max(a, b int) int {
if a > b {
return a
}
return b
}// Divide and Conquer Idea
// Definition: Given a node, return the maximum depth of the binary tree rooted at that node
var maxDepth = function(root) {
if (root === null) {
return 0;
}
// Use the definition to calculate the maximum depth of the left and right subtrees
var leftMax = maxDepth(root.left);
var rightMax = maxDepth(root.right);
// Derive the maximum depth of the original binary tree based
// on the maximum depth of the left and right subtrees
// The maximum depth of the entire tree is the maximum of the left and right subtree depths,
// plus one for the root node itself
return 1 + Math.max(leftMax, rightMax);
};Visualization of the Problem Decomposition Idea
As long as you clearly define the recursive function, this solution is not difficult to understand. But why is the main logic concentrated at the post-order position?
The core of this correct idea is that you can indeed derive the depth of the original tree from the maximum depth of its subtrees. So, you must first use the recursive function to calculate the maximum depth of the left and right subtrees, and then derive the maximum depth of the original tree. Naturally, the main logic is placed at the post-order position.
If you understand the two approaches to the maximum depth problem, then let's revisit the most basic binary tree pre-order, in-order, and post-order traversals, such as LeetCode Problem 144 "Binary Tree Preorder Traversal," which asks you to calculate the pre-order traversal result.
The familiar solution is the "traverse" approach, which I think needs no further explanation:
// Calculate the preorder traversal result using the traversal idea
class Solution {
// store the result of the preorder traversal
List<Integer> res = new LinkedList<>();
public List<Integer> preorderTraversal(TreeNode root) {
traverse(root);
return res;
}
// binary tree traversal function
void traverse(TreeNode root) {
if (root == null) {
return;
}
// preorder position
res.add(root.val);
traverse(root.left);
traverse(root.right);
}
}// Calculate the preorder traversal result using the traversal idea
class Solution {
public:
// store the result of the preorder traversal
vector<int> res;
vector<int> preorderTraversal(TreeNode* root) {
traverse(root);
return res;
}
// binary tree traversal function
void traverse(TreeNode* root) {
if (root == nullptr) {
return;
}
// preorder position
res.push_back(root->val);
traverse(root->left);
traverse(root->right);
}
};# Calculate the preorder traversal result using the traversal idea
class Solution:
def __init__(self):
self.res = []
def preorderTraversal(self, root: TreeNode) -> List[int]:
self.traverse(root)
return self.res
# binary tree traversal function
def traverse(self, root: TreeNode):
if root is None:
return
# preorder position
self.res.append(root.val)
self.traverse(root.left)
self.traverse(root.right)// Calculate the preorder traversal result using the traversal idea
func preorderTraversal(root *TreeNode) []int {
// store the result of the preorder traversal
var res []int
var traverse func(root *TreeNode)
traverse = func(root *TreeNode) {
if root == nil {
return
}
// preorder position
res = append(res, root.Val)
traverse(root.Left)
traverse(root.Right)
}
traverse(root)
return res
}// Calculate the preorder traversal result using the traversal idea
var preorderTraversal = function(root) {
// store the result of the preorder traversal
var res = [];
// binary tree traversal function
var traverse = function(root) {
if (root == null) {
return;
}
// preorder position
res.push(root.val);
traverse(root.left);
traverse(root.right);
};
traverse(root);
return res;
}But can you use the "decompose problem" approach to calculate the pre-order traversal result?
In other words, without using auxiliary functions like traverse or any external variables, can you solve the problem using only the preorderTraverse function provided by the problem?
We know the characteristic of pre-order traversal is that the root node's value is at the forefront, followed by the pre-order traversal result of the left subtree, and finally the pre-order traversal result of the right subtree:
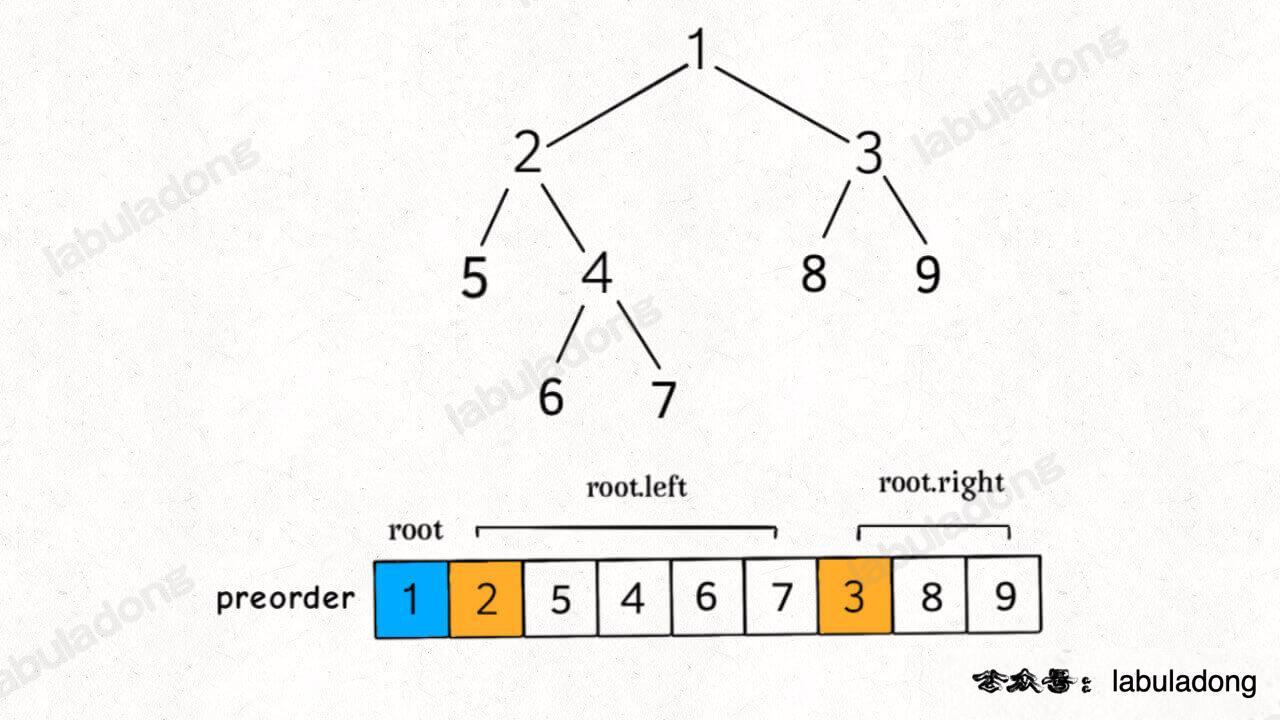
This allows for problem decomposition: the pre-order traversal result of a binary tree = root node + pre-order traversal result of the left subtree + pre-order traversal result of the right subtree.
Therefore, you can implement the pre-order traversal algorithm like this:
class Solution {
// Definition: Given the root node of a binary tree,
// return the preorder traversal result of this tree
List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new LinkedList<>();
if (root == null) {
return res;
}
// The result of preorder traversal, root.val is first
res.add(root.val);
// Using the function definition, followed by the
// preorder traversal result of the left subtree
res.addAll(preorderTraversal(root.left));
// Using the function definition, finally followed by the
// preorder traversal result of the right subtree
res.addAll(preorderTraversal(root.right)); return res;
}
}
return res;
}
}class Solution {
public:
// Definition: Given the root node of a binary tree,
// return the preorder traversal result of this tree
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
if (root == nullptr) {
return res;
}
// The result of preorder traversal, root->val is the first element
res.push_back(root->val);
// Using the function definition, followed by the
// preorder traversal result of the left subtree
vector<int> left = preorderTraversal(root->left);
res.insert(res.end(), left.begin(), left.end());
// Using the function definition, followed by the
// preorder traversal result of the right subtree
vector<int> right = preorderTraversal(root->right);
res.insert(res.end(), right.begin(), right.end()); return res;
}
};
return res;
}
};class Solution:
# Definition: Given the root of a binary tree, return the preorder traversal of this tree
def preorderTraversal(self, root):
res = []
if root == None:
return res
# In the preorder traversal result, root.val is the first
res.append(root.val)
# Use the function definition to append the
# preorder traversal result of the left subtree
res.extend(self.preorderTraversal(root.left))
# Use the function definition to append the
# preorder traversal result of the right subtree
res.extend(self.preorderTraversal(root.right))  return res
return res// Definition: Given the root of a binary tree,
// return the preorder traversal result of this tree.
func preorderTraversal(root *TreeNode) []int {
var res []int
if root == nil {
return res
}
// In preorder traversal, root.Val is the first element.
res = append(res, root.Val)
// According to the function definition, append the
// preorder traversal result of the left subtree.
res = append(res, preorderTraversal(root.Left)...)
// According to the function definition, append the
// preorder traversal result of the right subtree.
res = append(res, preorderTraversal(root.Right)...) return res
}
return res
}// Definition: Given the root node of a binary tree,
// return the preorder traversal result of this tree
var preorderTraversal = function(root) {
var res = [];
if (root == null) {
return res;
}
// The result of preorder traversal, root.val is the first
res.push(root.val);
// Using function definition, followed by the preorder traversal result of the left subtree
res = res.concat(preorderTraversal(root.left));
// Using function definition, finally followed by the
// preorder traversal result of the right subtree
res = res.concat(preorderTraversal(root.right)); return res;
}
return res;
}Inorder and postorder traversals are similar; you just need to place add(root.val) at the corresponding position for inorder and postorder traversals.
This solution is concise, but why is it not commonly seen?
One reason is the complexity of this algorithm is hard to manage, and it heavily depends on language features.
In Java, whether using ArrayList or LinkedList, the complexity of the addAll method is O(N), so the overall worst-case time complexity can reach O(N^2). This can be avoided if you implement an addAll method with O(1) complexity yourself. This is achievable with linked lists, as multiple lists can be connected with simple pointer operations.
Of course, the main reason is that textbooks never teach it this way...
The above mentioned a couple of simple examples, but there are many binary tree problems that can be solved using both approaches. It requires practice and thought on your part, not just sticking to one familiar method.
In summary, the general thought process when encountering a binary tree problem is:
1. Can the answer be obtained by traversing the binary tree once? If so, use a traverse function with external variables.
2. Can you define a recursive function to derive the answer to the original problem from the answers to subproblems (subtrees)? If so, write this recursive function's definition and make full use of its return value.
3. Regardless of the approach, understand what each node of the binary tree needs to do and when it should be done (preorder, inorder, postorder).
Our site’s Special Binary Tree Recursion Practice lists over 100 binary tree exercises, guiding you step-by-step using the above two thought processes to help you fully master recursive thinking and better understand advanced algorithms.
Special Characteristics of Postorder Position
Before discussing postorder position, let's briefly talk about preorder and inorder.
The preorder position itself doesn't have any special properties. The reason you might find many problems have code written in the preorder position is due to our habit of placing code that isn't sensitive to the position in preorder.
The inorder position is mainly used in BST scenarios; you can completely consider the inorder traversal of a BST as traversing a sorted array.
Key Points
Observe carefully, the capabilities of code in preorder, inorder, and postorder positions increase sequentially.
Code in the preorder position can only obtain data passed from parent nodes through function parameters.
Code in the inorder position can obtain parameter data as well as data passed back by the left subtree through function return values.
Code in the postorder position is the most powerful, as it can obtain parameter data and simultaneously receive data from both left and right subtrees through function return values.
Therefore, in some cases, moving code to the postorder position is the most efficient; some tasks can only be accomplished by code in the postorder position.
Let's look at some specific examples to understand the differences in their capabilities. Given a binary tree, here are two simple questions:
If the root node is considered as level 1, how do you print the level of each node?
How do you print the number of nodes in the left and right subtrees of each node?
The code for the first question can be written as follows:
// Binary tree traversal function
void traverse(TreeNode root, int level) {
if (root == null) {
return;
}
// Preorder position
printf("Node %s is at level %d", root.val, level);
traverse(root.left, level + 1);
traverse(root.right, level + 1);
}
// Call it like this
traverse(root, 1);The code for the second question can be written as follows:
// Definition: Given a binary tree, return the total number of nodes in it
int count(TreeNode root) {
if (root == null) {
return 0;
}
int leftCount = count(root.left);
int rightCount = count(root.right);
// Postorder position
printf("Node %s has %d nodes in the left subtree and %d nodes in the right subtree",
root, leftCount, rightCount);
return leftCount + rightCount + 1;
}The Key Difference Between These Two Problems
You can easily record the level of a node as you traverse from the root. You can pass the level using the function parameters in recursion. But to count the number of nodes in the subtree rooted at a node, you must traverse the whole subtree first, then return the answer using the function's return value.
With these two simple problems, you can see the feature of the postorder position: only in postorder can you get information about the subtree from the return value.
In other words, if the problem is related to the subtree, you usually need to set a proper return value for your function and write code in the postorder position.
Next, let's see how the postorder position is used in real problems. Let's look at LeetCode Problem 543: Diameter of Binary Tree. The problem asks you to find the longest diameter of a binary tree.
The "diameter" of a binary tree means the length of the path between any two nodes. The longest diameter does not have to go through the root. For example, look at this binary tree:
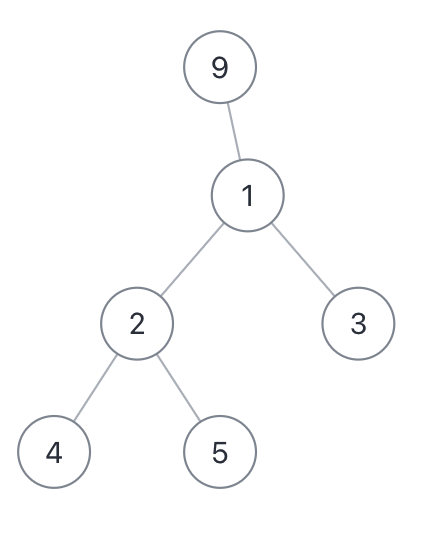
Its longest diameter is 3, that is, the length of [4,2,1,3], [4,2,1,9], or [5,2,1,3].
The key to solving this problem is: the "diameter" at each node equals the sum of the maximum depth of its left and right subtrees.
To find the longest diameter in the whole tree, the straightforward idea is to traverse every node, for each node calculate the diameter using the maximum depth of its left and right subtrees, then take the maximum among all diameters.
We have already written the code for maximum depth. Using this idea, we can write the following code:
class Solution {
// record the length of the maximum diameter
int maxDiameter = 0;
public int diameterOfBinaryTree(TreeNode root) {
// calculate the diameter for each node and find the maximum diameter
traverse(root);
return maxDiameter;
}
// traverse the binary tree
void traverse(TreeNode root) {
if (root == null) {
return;
}
// calculate the diameter for each node
int leftMax = maxDepth(root.left);
int rightMax = maxDepth(root.right);
int myDiameter = leftMax + rightMax;
// update the global maximum diameter
maxDiameter = Math.max(maxDiameter, myDiameter);
traverse(root.left);
traverse(root.right);
}
// calculate the maximum depth of the binary tree
int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
int leftMax = maxDepth(root.left);
int rightMax = maxDepth(root.right);
return 1 + Math.max(leftMax, rightMax);
}
}class Solution {
public:
// record the length of the maximum diameter
int maxDiameter = 0;
int diameterOfBinaryTree(TreeNode* root) {
// calculate the diameter for each node and find the maximum diameter
traverse(root);
return maxDiameter;
}
private:
// traverse the binary tree
void traverse(TreeNode* root) {
if (root == nullptr) {
return;
}
// calculate the diameter for each node
int leftMax = maxDepth(root->left);
int rightMax = maxDepth(root->right);
int myDiameter = leftMax + rightMax;
// update the global maximum diameter
maxDiameter = max(maxDiameter, myDiameter);
traverse(root->left);
traverse(root->right);
}
// calculate the maximum depth of the binary tree
int maxDepth(TreeNode* root) {
if (root == nullptr) {
return 0;
}
int leftMax = maxDepth(root->left);
int rightMax = maxDepth(root->right);
return 1 + max(leftMax, rightMax);
}
};class Solution:
def __init__(self):
# record the length of the maximum diameter
self.maxDiameter = 0
def diameterOfBinaryTree(self, root):
# calculate the diameter for each node, find the maximum diameter
self.traverse(root)
return self.maxDiameter
# traverse the binary tree
def traverse(self, root):
if root is None:
return
# calculate the diameter for each node
leftMax = self.maxDepth(root.left)
rightMax = self.maxDepth(root.right)
myDiameter = leftMax + rightMax
# update the global maximum diameter
self.maxDiameter = max(self.maxDiameter, myDiameter)
self.traverse(root.left)
self.traverse(root.right)
# calculate the maximum depth of the binary tree
def maxDepth(self, root):
if root is None:
return 0
leftMax = self.maxDepth(root.left)
rightMax = self.maxDepth(root.right)
return 1 + max(leftMax, rightMax)// record the length of the maximum diameter
func diameterOfBinaryTree(root *TreeNode) int {
maxDiameter := 0
// traverse the binary tree
var traverse func(root *TreeNode)
traverse = func(root *TreeNode) {
if root == nil {
return
}
// calculate the diameter for each node
leftMax := maxDepth(root.Left)
rightMax := maxDepth(root.Right)
myDiameter := leftMax + rightMax
// update the global maximum diameter
maxDiameter = max(maxDiameter, myDiameter)
traverse(root.Left)
traverse(root.Right)
}
traverse(root)
return maxDiameter
}
// calculate the maximum depth of the binary tree
func maxDepth(root *TreeNode) int {
if root == nil {
return 0
}
leftMax := maxDepth(root.Left)
rightMax := maxDepth(root.Right)
return 1 + max(leftMax, rightMax)
}
// helper function to find the maximum of two numbers
func max(a, b int) int {
if a > b {
return a
}
return b
}var diameterOfBinaryTree = function(root) {
// record the length of the maximum diameter
let maxDiameter = 0;
// calculate the maximum depth of the binary tree
const maxDepth = function(root) {
if (root === null) {
return 0;
}
let leftMax = maxDepth(root.left);
let rightMax = maxDepth(root.right);
return 1 + Math.max(leftMax, rightMax);
};
// traverse the binary tree
const traverse = function(root) {
if (root === null) {
return;
}
// calculate the diameter for each node
let leftMax = maxDepth(root.left);
let rightMax = maxDepth(root.right);
let myDiameter = leftMax + rightMax;
// update the global maximum diameter
maxDiameter = Math.max(maxDiameter, myDiameter);
traverse(root.left);
traverse(root.right);
};
traverse(root);
return maxDiameter;
};This solution is correct, but it runs very slowly. The reason is clear: traverse visits every node, and at each node it calls the recursive function maxDepth, which itself traverses all nodes in the subtree. So the worst time complexity is O(N^2).
Here is the situation we discussed before: preorder cannot get information from subtrees, so each node has to call maxDepth to get the depth of its subtrees.
How can we improve it? We should put the logic for calculating the diameter in the postorder position, more specifically, in the postorder of the maxDepth function, because in postorder we already know the maximum depth of the left and right subtrees.
So, change the code a bit and we get a better solution:
class Solution {
// record the length of the maximum diameter
int maxDiameter = 0;
public int diameterOfBinaryTree(TreeNode root) {
maxDepth(root);
return maxDiameter;
}
int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
int leftMax = maxDepth(root.left);
int rightMax = maxDepth(root.right);
// post-order position, calculate the maximum diameter by the way
int myDiameter = leftMax + rightMax;
maxDiameter = Math.max(maxDiameter, myDiameter);
return 1 + Math.max(leftMax, rightMax);
}
}class Solution {
// record the length of the maximum diameter
int maxDiameter = 0;
public:
int diameterOfBinaryTree(TreeNode* root) {
maxDepth(root);
return maxDiameter;
}
int maxDepth(TreeNode* root) {
if (root == nullptr) {
return 0;
}
int leftMax = maxDepth(root->left);
int rightMax = maxDepth(root->right);
// post-order position, calculate the maximum diameter along the way
int myDiameter = leftMax + rightMax;
maxDiameter = max(maxDiameter, myDiameter);
return 1 + max(leftMax, rightMax);
}
};class Solution:
def __init__(self):
# record the length of the maximum diameter
self.maxDiameter = 0
def diameterOfBinaryTree(self, root):
self.maxDepth(root)
return self.maxDiameter
def maxDepth(self, root):
if root is None:
return 0
leftMax = self.maxDepth(root.left)
rightMax = self.maxDepth(root.right)
# post-order position, by the way, calculate the maximum diameter
myDiameter = leftMax + rightMax
self.maxDiameter = max(self.maxDiameter, myDiameter)
return 1 + max(leftMax, rightMax)func diameterOfBinaryTree(root *TreeNode) int {
// record the length of the maximum diameter
maxDiameter := 0
var maxDepth func(root *TreeNode) int
maxDepth = func(root *TreeNode) int {
if root == nil {
return 0
}
leftMax := maxDepth(root.Left)
rightMax := maxDepth(root.Right)
// in post-order position, calculate the maximum diameter
myDiameter := leftMax + rightMax
maxDiameter = max(maxDiameter, myDiameter)
return 1 + max(leftMax, rightMax)
}
maxDepth(root)
return maxDiameter
}
func max(a, b int) int {
if a > b {
return a
}
return b
}var diameterOfBinaryTree = function(root) {
let maxDiameter = 0;
const maxDepth = function(root) {
if (root === null) {
return 0;
}
let leftMax = maxDepth(root.left);
let rightMax = maxDepth(root.right);
// in post-order position, calculate the maximum diameter
let myDiameter = leftMax + rightMax;
maxDiameter = Math.max(maxDiameter, myDiameter);
return 1 + Math.max(leftMax, rightMax);
}
maxDepth(root);
return maxDiameter;
};Algorithm Visualization
Now the time complexity is only O(N), the same as maxDepth.
To sum up: when you see a subtree problem, first think about setting a return value for the function, and work in the postorder position.
Info
Thinking Question: For problems that use postorder, do you use the "traverse" idea or the "divide problem" idea?
Click to Show Answer
For problems using postorder, you usually use the "divide problem" idea. The current node receives and uses the information returned from its subtrees, which means you break the problem into the current node plus the left and right subproblems.
If you wrote a recursive-in-recursive solution like the first one, you should think if you can optimize it using postorder.
For more exercises using postorder, see Binary Tree Postorder Practice, BST Postorder Practice, and Practice: Solve by Postorder.
The Difference and Connection Between DP, Backtracking, and DFS from the Tree Perspective
Earlier, I said that dynamic programming (DP) and backtracking are two different ways to solve binary tree problems. If you are reading this, you probably agree with this idea. Some careful readers often ask: Your way of thinking is very clear, but you rarely talk about DFS?
In fact, in my article Solving All Island Problems in One Go, I used DFS. But I have not written a separate article just for DFS. This is because DFS and backtracking are very similar. The difference is only in the details.
What is this detail? The difference is about whether "make a choice" and "undo a choice" are inside or outside the for loop. In DFS, it is outside. In backtracking, it is inside.
Why is there this difference? We need to understand it together with the binary tree structure. In this part, I will use one sentence to explain the classic ideas of backtracking, DFS, and DP, and how they are connected to binary tree problems:
Key Point
DP, DFS, and backtracking can all be seen as extensions of binary tree problems. The difference is what they focus on:
- Dynamic Programming (DP) is about breaking down problems (divide and conquer). It focuses on the whole "subtree".
- Backtracking is about traversal. It focuses on the "branches" between nodes.
- DFS is also about traversal. It focuses on one "node" at a time.
How to understand this? Let me give three examples.
Example 1: Breaking Down the Problem
First example: Given a binary tree, write a count function to calculate the number of nodes in the tree using the divide and conquer idea. The code is simple and was shown before:
// Definition: input a binary tree, return the total number of nodes in this binary tree
int count(TreeNode root) {
if (root == null) {
return 0;
}
// The current node cares about the total number of nodes in each of its subtrees
// Because the result of the subproblems can be used
// to derive the result of the original problem
int leftCount = count(root.left);
int rightCount = count(root.right);
// In the postorder position, the total number of nodes in the left and right subtrees
// plus the current node itself is the total number of nodes in the entire tree
return leftCount + rightCount + 1;
}// Definition: Given a binary tree, return the total number of nodes in this binary tree
int count(TreeNode* root) {
if (root == nullptr) {
return 0;
}
// The current node cares about the total number of nodes in the two subtrees
// Because the result of the subproblems can derive the result of the original problem
int leftCount = count(root->left);
int rightCount = count(root->right);
// In the post-order position, the number of nodes in the left and right
// subtrees plus itself is the total number of nodes in the entire tree
return leftCount + rightCount + 1;
}# Definition: Given a binary tree, return the total number of nodes in the tree
def count(root):
if root is None:
return 0
# The current node is concerned with the total number of nodes in its two subtrees
# Because the result of the subproblems can be used
# to derive the result of the original problem
leftCount = count(root.left)
rightCount = count(root.right)
# In the post-order position, the total number of nodes in the left and right
# subtrees plus the current node equals the total number of nodes in the tree
return leftCount + rightCount + 1// Definition: Given a binary tree, return the total number of nodes in the tree
func count(root *TreeNode) int {
if root == nil {
return 0
}
// The current node cares about the total number of nodes in its left and right subtrees
// Because the result of the sub-problems can be used
// to derive the result of the original problem
leftCount := count(root.Left)
rightCount := count(root.Right)
// In post-order position, the number of nodes in the left and right
// subtrees plus the current node is the total number of nodes in the tree
return leftCount + rightCount + 1
}// Definition: Given a binary tree, return the total number of nodes in this binary tree
var count = function(root) {
if (root == null) {
return 0;
}
// The current node cares about the total number of nodes in its two subtrees
// Because the result of the subproblems can be used
// to derive the result of the original problem
var leftCount = count(root.left);
var rightCount = count(root.right);
// In the post-order position, the number of nodes in the left and right
// subtrees plus itself is the total number of nodes in the entire tree
return leftCount + rightCount + 1;
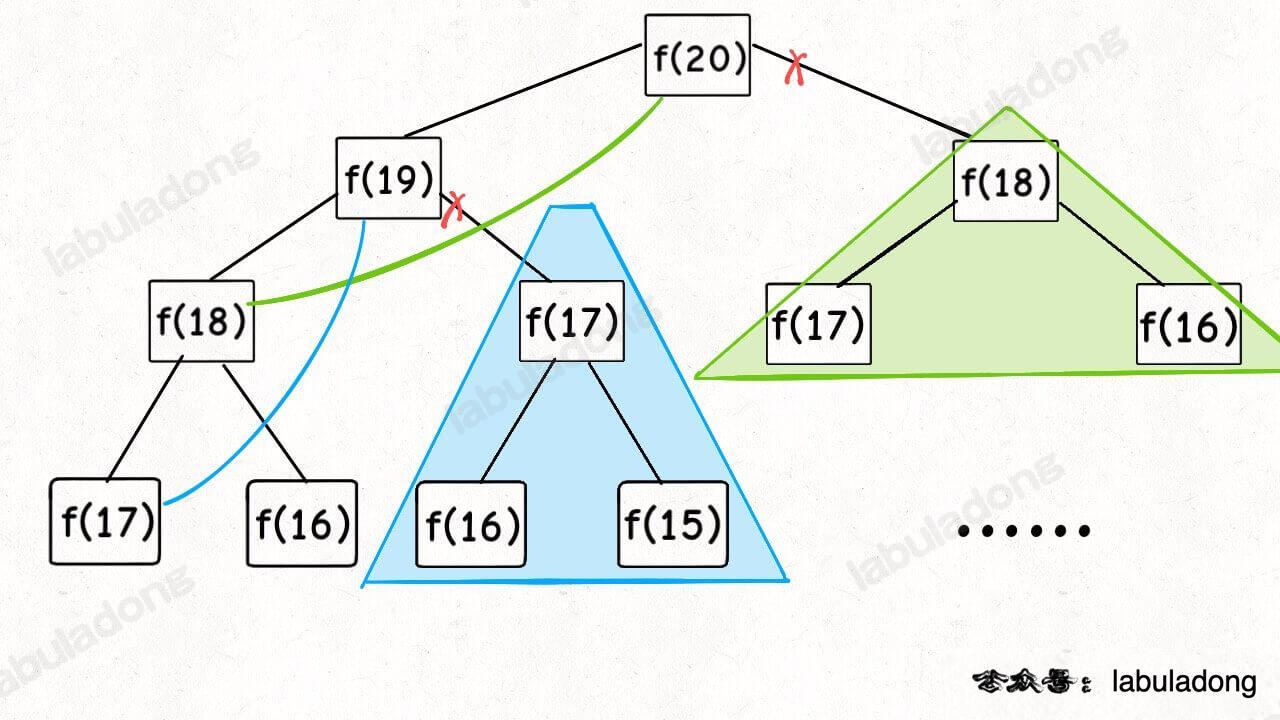
}You see, this is the dynamic programming way of breaking down a problem. The focus is always on the same structure of subproblems, which is the "subtree" in a binary tree.
Take another example from DP. In Detailed Dynamic Programming Framework, the Fibonacci example is given. Our focus is always on the return values of subtrees:
// f(n) calculates the nth Fibonacci number
int fib(int n) {
// base case
if (n == 0 || n == 1){
return n;
}
return fib(n - 1) + fib(n - 2);
}// f(n) calculates the nth Fibonacci number
int fib(int n) {
// base case
if (n == 0 || n == 1){
return n;
}
return fib(n - 1) + fib(n - 2);
}# f(n) calculates the nth Fibonacci number
def fib(n: int) -> int:
# base case
if n == 0 or n == 1:
return n
return fib(n - 1) + fib(n - 2)// f(n) calculates the nth Fibonacci number
func fib(n int) int {
// base case
if n == 0 || n == 1 {
return n
}
return fib(n-1) + fib(n-2)
}// f(n) calculates the nth Fibonacci number
var fib = function(n) {
// base case
if (n == 0 || n == 1) {
return n;
}
return fib(n - 1) + fib(n - 2);
};
Example 2: The Idea of Backtracking Algorithm
Second example, given a binary tree, please write a traverse function to print the traversal process of this tree. Here is the code:
void traverse(TreeNode root) {
if (root == null) return;
printf("Go from node %s to node %s", root, root.left);
traverse(root.left);
printf("Return from node %s to node %s", root.left, root);
printf("Go from node %s to node %s", root, root.right);
traverse(root.right);
printf("Return from node %s to node %s", root.right, root);
}This is easy to understand. Now, let's upgrade the binary tree to an N-ary tree. The code is similar:
// N-ary tree node
class Node {
int val;
Node[] children;
}
void traverse(Node root) {
if (root == null) return;
for (Node child : root.children) {
printf("Go from node %s to node %s", root, child);
traverse(child);
printf("Return from node %s to node %s", child, root);
}
}This N-ary tree traversal framework can be extended to the Backtracking Algorithm Framework:
// Backtracking algorithm framework
void backtrack(...) {
// base case
if (...) return;
for (int i = 0; i < ...; i++) {
// Make a choice
...
// Go to the next level of the decision tree
backtrack(...);
// Undo the previous choice
...
}
}You see, this is the backtracking algorithm's way of traversal. The focus is always on the process of moving between nodes. In a binary tree, you can think of it as "branches."
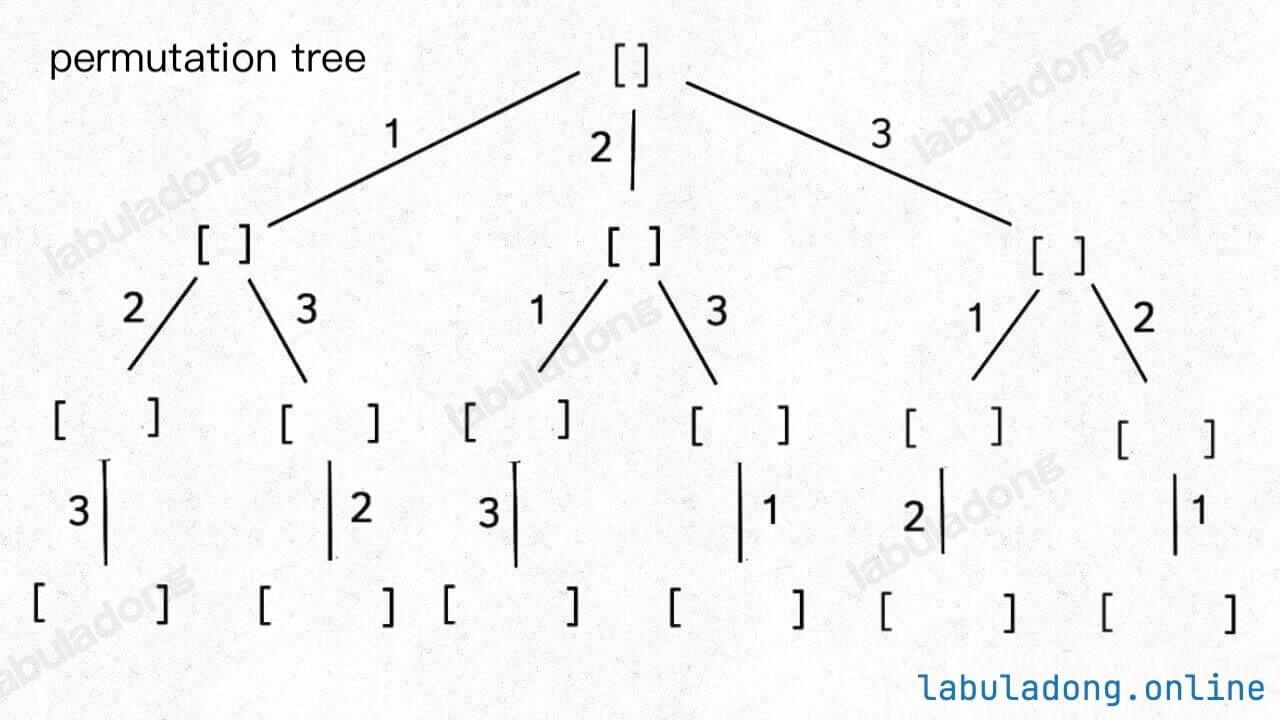
Look at a specific backtracking problem, for example, the permutations problem in Backtracking: Subsets, Permutations, and Combinations. Here, we pay attention to each branch:
// Core part of the backtracking algorithm
void backtrack(int[] nums) {
// Backtracking framework
for (int i = 0; i < nums.length; i++) {
// Make a choice
used[i] = true;
track.addLast(nums[i]);
// Move to the next level of backtracking tree
backtrack(nums);
// Undo the choice
track.removeLast();
used[i] = false;
}
}
Example 3: The Idea of DFS
For the third example, I give you a binary tree. Please write a traverse function to add 1 to the value of every node in the tree. This is simple. The code is as follows:
void traverse(TreeNode root) {
if (root == null) return;
// increment the value of each traversed node by one
root.val++;
traverse(root.left);
traverse(root.right);
}void traverse(TreeNode* root) {
if (root == nullptr) return;
// increment the value of each traversed node by one
root->val++;
traverse(root->left);
traverse(root->right);
}def traverse(root):
if root is None:
return
# increment the value of each traversed node by one
root.val += 1
traverse(root.left)
traverse(root.right)func traverse(root *TreeNode) {
if root == nil {
return
}
// increment the value of each visited node by one
root.Val++
traverse(root.Left)
traverse(root.Right)
}var traverse = function(root) {
if (root === null) return;
// increment the value of each traversed node by one
root.val++;
traverse(root.left);
traverse(root.right);
}This is the idea of DFS algorithm. It always focuses on a single node. In a binary tree, it means processing each “node”.
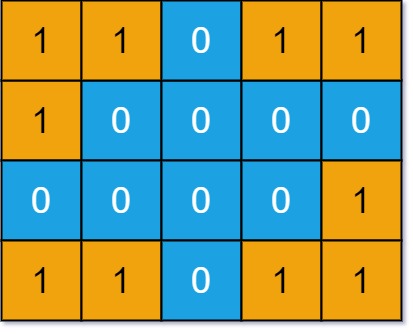
Look at some real DFS problems, such as the first few questions in Killer Guide to Island Problems. There, we focus on each cell (node) in the grid array. We need to process the cells we have visited, so we use DFS to solve these problems:
// Core logic of DFS algorithm
void dfs(int[][] grid, int i, int j) {
int m = grid.length, n = grid[0].length;
if (i < 0 || j < 0 || i >= m || j >= n) {
return;
}
if (grid[i][j] == 0) {
return;
}
// Mark each visited cell as 0
grid[i][j] = 0;
dfs(grid, i + 1, j);
dfs(grid, i, j + 1);
dfs(grid, i - 1, j);
dfs(grid, i, j - 1);
}
Now, think carefully about the three simple examples above. As I said: Dynamic programming focuses on the whole “subtree”, backtracking focuses on the “branches” (connections between nodes), and DFS focuses on each “node”.
With this background, it’s easier to understand why the “make a choice” and “undo a choice” steps are at different places in backtracking and DFS code. Look at the two pieces of code below:
// DFS algorithm puts the logic of "making a choice" and "undoing a choice" outside the for loop
void dfs(Node root) {
if (root == null) return;
// make a choice
print("enter node %s", root);
for (Node child : root.children) {
dfs(child);
}
// undo a choice
print("leave node %s", root);
}
// Backtracking algorithm puts the logic of "making a
// choice" and "undoing a choice" inside the for loop
void backtrack(Node root) {
if (root == null) return;
for (Node child : root.children) {
// make a choice
print("I'm on the branch from %s to %s", root, child);
backtrack(child);
// undo a choice
print("I'll leave the branch from %s to %s", child, root);
}
}// In DFS algorithm, the logic of "making a choice" and
// "undoing a choice" is placed outside the for loop
void dfs(Node* root) {
if (!root) return;
// make a choice
printf("enter node %s\n", root->val.c_str());
for (Node* child : root->children) {
dfs(child);
}
// undo a choice
printf("leave node %s\n", root->val.c_str());
}
// In backtracking algorithm, the logic of "making a
// choice" and "undoing a choice" is placed inside the for loop
void backtrack(Node* root) {
if (!root) return;
for (Node* child : root->children) {
// make a choice
printf("I'm on the branch from %s to %s\n", root->val.c_str(), child->val.c_str());
backtrack(child);
// undo a choice
printf("I'll leave the branch from %s to %s\n", child->val.c_str(), root->val.c_str());
}
}# The DFS algorithm puts the logic of "making a
# choice" and "undoing a choice" outside the for loop
def dfs(root):
if root is None:
return
# make a choice
print("enter node %s" % root)
for child in root.children:
dfs(child)
# undo a choice
print("leave node %s" % root)
# The backtracking algorithm puts the logic of "making
# a choice" and "undoing a choice" inside the for loop
def backtrack(root):
if root is None:
return
for child in root.children:
# make a choice
print("I'm on the branch from %s to %s" % (root, child))
backtrack(child)
# undo a choice
print("I'll leave the branch from %s to %s" % (child, root))import "fmt"
// The DFS algorithm places the logic of "making
// choices" and "undoing choices" outside the for loop
func Dfs(root *Node) {
if root == nil {
return
}
// make a choice
fmt.Printf("enter node %v\n", root)
for _, child := range root.children {
Dfs(child)
}
// undo the choice
fmt.Printf("leave node %v\n", root)
}
// The backtracking algorithm places the logic of
// "making choices" and "undoing choices" inside the for loop
func Backtrack(root *Node) {
if root == nil {
return
}
for _, child := range root.children {
// make a choice
fmt.Printf("I'm on the branch from %v to %v\n", root, child)
Backtrack(child)
// undo the choice
fmt.Printf("I'll leave the branch from %v to %v\n", child, root)
}
}// DFS algorithm places the logic of "making choices" and "undoing choices" outside the for loop
var dfs = function(root) {
if (root == null) return;
// make choices
console.log("enter node %s", root);
for (var i = 0; i < root.children.length; i++) {
dfs(root.children[i]);
}
// undo choices
console.log("leave node %s", root);
}
// Backtracking algorithm places the logic of "making
// choices" and "undoing choices" inside the for loop
var backtrack = function(root) {
if (root == null) return;
for (var i = 0; i < root.children.length; i++) {
var child = root.children[i];
// make choices
console.log("I'm on the branch from %s to %s", root, child);
backtrack(child);
// undo choices
console.log("I'll leave the branch from %s to %s", child, root);
}
}See? In the backtracking algorithm, you must put “make a choice” and “undo a choice” inside the for loop. Otherwise, how can you get both ends of a “branch”?
Level Order Traversal
Binary tree questions are mainly for practicing recursion. But level order traversal is an iterative method, and it’s simple. Here is the basic code structure:
// Input the root node of a binary tree, perform level-order traversal on the binary tree
void levelTraverse(TreeNode root) {
if (root == null) return;
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
int depth = 1;
// Traverse each level of the binary tree from top to bottom
while (!q.isEmpty()) {
int sz = q.size();
// Traverse each node of the level from left to right
for (int i = 0; i < sz; i++) {
TreeNode cur = q.poll();
// put the nodes of the next level into the queue
if (cur.left != null) {
q.offer(cur.left);
}
if (cur.right != null) {
q.offer(cur.right);
}
}
depth++;
}
}// input the root node of a binary tree, perform a level order traversal of the tree
int levelTraverse(TreeNode* root) {
if (root == nullptr) return;
queue<TreeNode*> q;
q.push(root);
int depth = 0;
// traverse each level of the binary tree from top to bottom
while (!q.empty()) {
int sz = q.size();
// traverse each node of the level from left to right
for (int i = 0; i < sz; i++) {
TreeNode* cur = q.front();
q.pop();
// put the nodes of the next level into the queue
if (cur->left != nullptr) {
q.push(cur->left);
}
if (cur->right != nullptr) {
q.push(cur->right);
}
}
depth++;
}
return depth;
}# input the root of a binary tree, perform level order traversal of this binary tree
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
if not root:
return
q = collections.deque()
q.append(root)
depth = 0
# traverse each level of the binary tree from top to bottom
while q:
sz = len(q)
# traverse each node of each level from left to right
for i in range(sz):
cur = q.popleft()
# put the nodes of the next level into the queue
if cur.left:
q.append(cur.left)
if cur.right:
q.append(cur.right)
depth += 1// Input the root node of a binary tree and perform level order traversal of this binary tree
func levelTraverse(root *TreeNode) {
if root == nil {
return
}
q := make([]*TreeNode, 0)
q = append(q, root)
depth := 1
// Traverse each level of the binary tree from top to bottom
for len(q) > 0 {
sz := len(q)
// Traverse each node of each level from left to right
for i := 0; i < sz; i++ {
cur := q[0]
q = q[1:]
// put the nodes of the next level into the queue
if cur.Left != nil {
q = append(q, cur.Left)
}
if cur.Right != nil {
q = append(q, cur.Right)
}
}
depth++
}
}// input the root node of a binary tree, perform level-order traversal of this binary tree
var levelTraverse = function(root) {
if (root == null) return;
var q = [];
q.push(root);
var depth = 1;
// traverse each level of the binary tree from top to bottom
while (q.length > 0) {
var sz = q.length;
// traverse each node of each level from left to right
for (var i = 0; i < sz; i++) {
var cur = q.shift();
// put the nodes of the next level into the queue
if (cur.left != null) {
q.push(cur.left);
}
if (cur.right != null) {
q.push(cur.right);
}
}
depth++;
}
}In this code, the while loop and the for loop help traverse from top to bottom and from left to right:
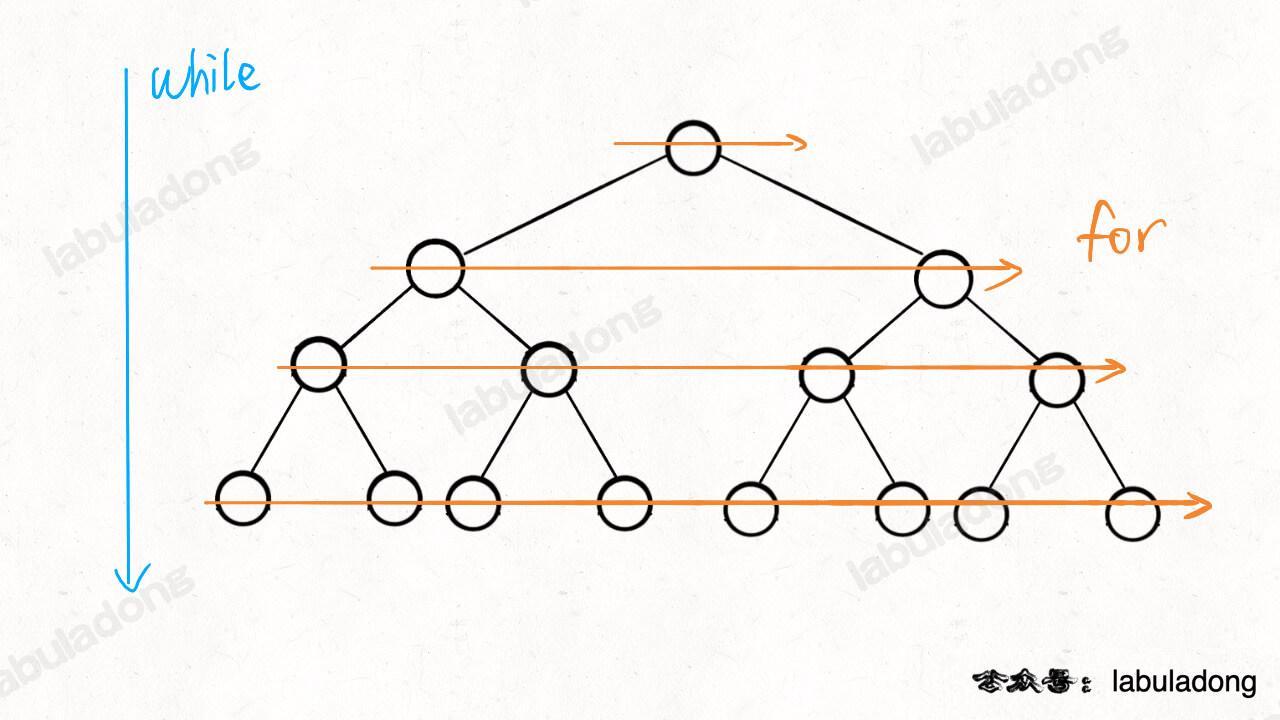
Earlier, in BFS Algorithm Framework, we explained how level order traversal in binary trees extends to BFS. BFS is often used to find the shortest path in an unweighted graph.
Of course, this framework can be changed flexibly. If the problem does not need to record the level (step), you can remove the for loop above. For example, in the Dijkstra Algorithm, which finds shortest path in a weighted graph, we discussed how to extend BFS.
It’s worth mentioning, some binary tree problems that seem to need level order traversal can also be solved using recursion. This can be tricky and tests how well you understand preorder, inorder, and postorder traversals.
Alright, this article is long enough. We have covered most of the common binary tree techniques related to traversal order. How much you can really use them depends on your own practice and thinking.
Finally, in Binary Tree Recursion Practice, I will guide you step by step to use the techniques discussed in this article.
Answering Questions from the Comments
Let me talk a bit more about level order traversal (and the BFS algorithm framework that comes from it).
If you know enough about binary trees, you might think of many ways to get the level order result using recursion, like the example below:
class Solution {
List<List<Integer>> res = new ArrayList<>();
public List<List<Integer>> levelTraverse(TreeNode root) {
if (root == null) {
return res;
}
// root is considered as level 0
traverse(root, 0);
return res;
}
void traverse(TreeNode root, int depth) {
if (root == null) {
return;
}
// pre-order position, check if nodes of depth level are already stored
if (res.size() <= depth) {
// first time entering depth level
res.add(new LinkedList<>());
}
// pre-order position, add root node's value at depth level
res.get(depth).add(root.val);
traverse(root.left, depth + 1);
traverse(root.right, depth + 1);
}
}class Solution {
public:
vector<vector<int>> res;
vector<vector<int>> levelTraverse(TreeNode* root) {
if (root == nullptr) {
return res;
}
// root is considered as level 0
traverse(root, 0);
return res;
}
void traverse(TreeNode* root, int depth) {
if (root == nullptr) {
return;
}
// in preorder position, check if the nodes of level depth are already stored
if (res.size() <= depth) {
// first time entering level depth
res.push_back(vector<int> {});
}
// in preorder position, add the value of root node to level depth
res[depth].push_back(root->val);
traverse(root->left, depth + 1);
traverse(root->right, depth + 1);
}
};class Solution:
def __init__(self):
self.res = []
def levelTraverse(self, root):
if root is None:
return self.res
# root is considered as level 0
self.traverse(root, 0)
return self.res
def traverse(self, root, depth):
if root is None:
return
# pre-order position, check if the nodes at level depth have already been stored
if len(self.res) <= depth:
# first time entering level depth
self.res.append([])
# pre-order position, add the value of root node at level depth
self.res[depth].append(root.val)
self.traverse(root.left, depth + 1)
self.traverse(root.right, depth + 1)func levelTraverse(root *TreeNode) [][]int {
res := make([][]int, 0)
if root == nil {
return res
}
// root is considered as level 0
traverse(root, 0, &res)
return res
}
func traverse(root *TreeNode, depth int, res *[][]int) {
if root == nil {
return
}
// in pre-order position, check if nodes at depth level are already stored
if len(*res) <= depth {
// entering depth level for the first time
*res = append(*res, make([]int, 0))
}
// in pre-order position, add the value of the root node at depth level
(*res)[depth] = append((*res)[depth], root.Val)
traverse(root.Left, depth+1, res)
traverse(root.Right, depth+1, res)
}var levelTraverse = function(){
res = [];
const traverse = function(root, depth) {
if (root === null) {
return;
}
// pre-order position, check if the nodes at depth level have been stored
if (res.length <= depth) {
// entering depth level for the first time
res.push([]);
}
// pre-order position, add the value of root node at depth level
res[depth].push(root.val);
traverse(root.left, depth + 1);
traverse(root.right, depth + 1);
}
// consider root as level 0
traverse(root, 0);
return res;
}This method does give you the level order result, but in essence, it is still a preorder traversal of the binary tree, or in other words, it uses DFS thinking, not true level order or BFS thinking. This is because the solution depends on preorder traversal's top-down, left-to-right order to get the right answer.
To put it simply, this solution is more like a "column order traversal" from left to right, not a "level order traversal" from top to bottom. So, for problems like finding the minimum distance, this solution works the same as DFS, and does not have the performance advantage of BFS.
Some readers also shared another recursive way to do level order traversal:
class Solution {
List<List<Integer>> res = new LinkedList<>();
public List<List<Integer>> levelTraverse(TreeNode root) {
if (root == null) {
return res;
}
List<TreeNode> nodes = new LinkedList<>();
nodes.add(root);
traverse(nodes);
return res;
}
void traverse(List<TreeNode> curLevelNodes) {
// base case
if (curLevelNodes.isEmpty()) {
return;
}
// pre-order position, calculate the values of the
// current level and the node list of the next level
List<Integer> nodeValues = new LinkedList<>();
List<TreeNode> nextLevelNodes = new LinkedList<>();
for (TreeNode node : curLevelNodes) {
nodeValues.add(node.val);
if (node.left != null) {
nextLevelNodes.add(node.left);
}
if (node.right != null) {
nextLevelNodes.add(node.right);
}
}
// add results in pre-order position to get top-down level order traversal
res.add(nodeValues);
traverse(nextLevelNodes);
// add results in post-order position to get bottom-up level order traversal
// res.add(nodeValues);
}
}class Solution {
private:
vector<vector<int>> res;
public:
vector<vector<int>> levelTraverse(TreeNode* root) {
if (root == NULL) {
return res;
}
vector<TreeNode*> nodes;
nodes.push_back(root);
traverse(nodes);
return res;
}
void traverse(vector<TreeNode*>& curLevelNodes) {
// base case
if (curLevelNodes.empty()) {
return;
}
// pre-order position, calculate the values of the current
// level and the list of nodes for the next level
vector<int> nodeValues;
vector<TreeNode*> nextLevelNodes;
for (TreeNode* node : curLevelNodes) {
nodeValues.push_back(node->val);
if (node->left != NULL) {
nextLevelNodes.push_back(node->left);
}
if (node->right != NULL) {
nextLevelNodes.push_back(node->right);
}
}
// add results in pre-order position to get top-down level order traversal
res.push_back(nodeValues);
traverse(nextLevelNodes);
// add results in post-order position to get bottom-up level order traversal
// res.push_back(nodeValues);
}
};class Solution:
def __init__(self):
self.res = []
def levelTraverse(self, root):
if not root:
return self.res
nodes = [root]
self.traverse(nodes)
return self.res
def traverse(self, curLevelNodes):
# base case
if not curLevelNodes:
return
# pre-order position, calculate the values of the current
# level and the list of nodes for the next level
nodeValues = []
nextLevelNodes = []
for node in curLevelNodes:
nodeValues.append(node.val)
if node.left:
nextLevelNodes.append(node.left)
if node.right:
nextLevelNodes.append(node.right)
# add results at pre-order position, can get top-down level order traversal
self.res.append(nodeValues)
self.traverse(nextLevelNodes)
# add results at post-order position, can get bottom-up level order traversal result
# res.append(nodeValues)// The converted levelTraverse function
func levelTraverse(root *TreeNode) [][]int {
res := [][]int{}
if root == nil {
return res
}
nodes := []*TreeNode{root}
traverse(nodes, &res)
return res
}
// The converted traverse function
func traverse(curLevelNodes []*TreeNode, res *[][]int) {
// base case
if len(curLevelNodes) == 0 {
return
}
// Preorder position, calculate the values of the
// current level and the list of nodes for the next level
nodeValues := []int{}
nextLevelNodes := []*TreeNode{}
for _, node := range curLevelNodes {
nodeValues = append(nodeValues, node.Val)
if node.Left != nil {
nextLevelNodes = append(nextLevelNodes, node.Left)
}
if node.Right != nil {
nextLevelNodes = append(nextLevelNodes, node.Right)
}
}
// Preorder position to add results, achieving top-down level order traversal
*res = append(*res, nodeValues)
// Traverse the next level
traverse(nextLevelNodes, res)
// Postorder position to add results, achieving bottom-up level order traversal
// *res = append(*res, nodeValues)
}var res = [];
var levelTraverse = function(root) {
if (root === null) {
return res;
}
let nodes = [];
nodes.push(root);
traverse(nodes);
return res;
};
var traverse = function(curLevelNodes) {
// base case
if (curLevelNodes.length === 0) {
return;
}
// pre-order position, calculate the values of the
// current level and the node list of the next level
let nodeValues = [];
let nextLevelNodes = [];
for (let node of curLevelNodes) {
nodeValues.push(node.val);
if (node.left !== null) {
nextLevelNodes.push(node.left);
}
if (node.right !== null) {
nextLevelNodes.push(node.right);
}
}
// add results at pre-order position to get top-down level order traversal
res.push(nodeValues);
traverse(nextLevelNodes);
// add results at post-order position to get bottom-up level order traversal
// res.push(nodeValues);
};The traverse function here is a bit like a recursive function for traversing a singly linked list. It treats each level of the binary tree as a node in a linked list.
Compared to the previous recursive solution, this one does a top-down "level order traversal." It is closer to the core idea of BFS. You can use this as a recursive way to implement BFS and expand your thinking.