BFS Algorithm Common Patterns and Code Template

labuladongOriginalAbout 9122 words

This article will resolve

LeetCode	Difficulty
752. Open the Lock	🟠
773. Sliding Puzzle	🔴

Prerequisites

Before reading this article, you need to learn:

I have said many times, algorithms like DFS, backtracking, and BFS are actually about turning a problem into a tree structure and then traversing that tree with brute-force search. So, the code for these brute-force algorithms is really just tree traversal code.

Let’s sort out the logic here:

The core of DFS and backtracking is to recursively traverse an "exhaustive tree" (an N-ary tree). And recursive traversal of an N-ary tree comes from recursive traversal of a binary tree. That’s why I say DFS and backtracking are really recursive traversal of binary trees.

The core of BFS is traversing a graph. As you will see soon, the BFS framework is just like the DFS/BFS traversal of graphs.

Graph traversal is basically N-ary tree traversal, but with a visited array to avoid infinite loops. And N-ary tree traversal comes from binary tree traversal. So I say, at its core, BFS is really level order traversal of a binary tree.

Why is BFS often used to solve shortest path problems? In When to Use DFS and BFS, I explained this in detail with the example of binary tree minimum depth.

In fact, all shortest path problems are similar to the minimum depth problem of a binary tree (finding the closest leaf node to the root). Recursive traversal must visit all nodes to find the target, but level order traversal can find the answer without visiting every node. That’s why level order traversal is good for shortest path problems.

Is this clear enough now?

So before reading this article, make sure you have learned Binary Tree Recursive/Level Order Traversal, N-ary Tree Recursive/Level Order Traversal, and DFS/BFS Traversal of Graphs. Once you understand how to traverse these basic data structures, other algorithms will be much easier to learn.

The main point of this article is to teach you how to turn real algorithm problems into abstract models, then use the BFS framework to solve them.

In real coding interviews, you won’t be directly asked to traverse a tree or graph. Instead, you’ll get a real-world problem, and you have to turn it into a standard graph or tree, then use BFS to find the answer.

For example, you are given a maze game and asked to find the minimum number of steps to reach the exit. If the maze has teleporters that instantly move you to another spot, what is the minimum number of steps then?

Or, given two words, you can change one into another by replacing, deleting, or inserting one character each time. What is the smallest number of operations needed?

Or, in a tile-matching game, two tiles can only be matched if the shortest line connecting them has at most two turns. When you click two tiles, how does the game check how many turns the line between them has?

At first, these problems don’t seem related to trees or graphs. But with a bit of abstraction, they are really just tree or graph traversal problems. They just look simple and boring.

Let’s use a few examples to show how to use the BFS framework, so you won’t find these problems hard anymore.

Algorithm Framework

The BFS framework is actually the same as the DFS/BFS Traversal of Graphs article. There are three ways to write BFS.

For real BFS problems, the first way is simple but not often used because it’s limited. The second way is the most common—most medium-level BFS problems can be solved this way. The third way is a bit more complex but more flexible. For harder problems, you may need the third way. In the next chapter, BFS Problems, you’ll see some hard questions that use the third way. You can try them yourself later.

The examples in this article are all medium difficulty, so the solutions are based on the second way:

java

// BFS traversal of the graph starting from s, and record the steps
// When the target node is reached, return the number of steps
int bfs(int s, int target) {
    boolean[] visited = new boolean[graph.size()];
    Queue<Integer> q = new LinkedList<>();
    q.offer(s);
    visited[s] = true;
    // record the number of steps taken from s to the current node
    int step = 0;
    while (!q.isEmpty()) {
        int sz = q.size();
        for (int i = 0; i < sz; i++) {
            int cur = q.poll();
            System.out.println("visit " + cur + " at step " + step);
            // determine if the target point is reached
            if (cur == target) {
                return step;
            }
            // add the neighbors to the queue to search around
            for (int to : neighborsOf(cur)) {
                if (!visited[to]) {
                    q.offer(to);
                    visited[to] = true;
                }
            }
        }
        step++;
    }
    // If we reach here, it means the target node was not found in the graph
    return -1;
}

cpp

// BFS traversal of the graph starting from s, and record the steps
// When the target node is reached, return the number of steps
int bfs(const Graph& graph, int s, int target) {
    vector<bool> visited(graph.size(), false);
    queue<int> q;
    q.push(s);
    visited[s] = true;
    // record the number of steps taken from s to the current node taken
    int step = 0;
    while (!q.empty()) {
        int sz = q.size();
        for (int i = 0; i < sz; i++) {
            int cur = q.front();
            q.pop();
            cout << "visit " << cur << " at step " << step << endl;
            // determine if the target point is reached
            if (cur == target) {
                return step;
            }
            // add the neighbors to the queue to search around
            for (int to : neighborsOf(cur)) {
                if (!visited[to]) {
                    q.push(to);
                    visited[to] = true;
                }
            }
        }
        step++;
    }
    // If we reach here, it means the target node was not found in the graph
    return -1;
}

python

# BFS traversal of the graph starting from s, and record the steps
def bfs(graph, s, target):
    visited = [False] * len(graph)
    q = deque([s])
    visited[s] = True
    # record the number of steps taken from s to the current node
    step = 0
    
    while q:
        sz = len(q)
        for i in range(sz):
            cur = q.popleft()
            print(f"visit {cur} at step {step}")
            # determine if the target point is reached
            if cur == target:
                return step

            # add neighboring nodes to the queue, and spread the search outward
            for to in neighborsOf(cur):
                if not visited[to]:
                    q.append(to)
                    visited[to] = True
        step += 1
    # If we reach here, it means the target node was not found in the graph
    return -1

// BFS traversal of the graph starting from s, and record the steps
// When the target node is reached, return the number of steps
func bfs(graph Graph, s int, target int) int {
    visited := make([]bool, graph.size())
    q := []int{s}
    visited[s] = true
    // record the number of steps taken from s to the current node in the traversal
    step := 0
    for len(q) > 0 {
        sz := len(q)
        for i := 0; i < sz; i++ {
            cur := q[0]
            q = q[1:]
            fmt.Printf("visit %d at step %d\n", cur, step)
            // determine if the target point is reached
            if cur == target {
                return step
            }

            // add the neighbors to the queue to search around
            for _, to := range neighborsOf(cur) {
                if !visited[to] {
                    q = append(q, to)
                    visited[to] = true
                }
            }
        }
        step++
    }
    // If we reach here, it means the target node was not found in the graph
    return -1
}

javascript

// BFS traversal of the graph starting from s, and record the steps
// When the target node is reached, return the number of steps
var bfs = function(graph, s, target) {
    var visited = new Array(graph.size()).fill(false);
    var q = [];
    q.push(s);
    visited[s] = true;
    // record the number of steps taken from s to the current node in the traversal
    var step = 0;

    while (q.length !== 0) {
        var sz = q.length;
        for (var i = 0; i < sz; i++) {
            var cur = q.shift();
            // visit the current node
            console.log("visit " + cur + " at step " + step);
            // determine if the target point is reached
            if (cur === target) {
                return step;
            }
            // add the neighbors to the queue to search around
            var neighbors = neighborsOf(cur);
            for (var i = 0; i < neighbors.length; i++) {
                var to = neighbors[i];
                if (!visited[to]) {
                    q.push(to);
                    visited[to] = true;
                }
            }
        }
        step++;
    }
    // If we reach here, it means the target node was not found in the graph
    return -1;
}

The code framework above is almost copied from DFS/BFS Traversal of Graphs. It just adds a target parameter, so when you reach the target for the first time, you stop and return the number of steps.

Next, let’s use a few examples to see how to use this framework.

Sliding Puzzle

LeetCode Problem 773 "Sliding Puzzle" is a problem that can be solved using the BFS framework. The problem is described as follows:

You are given a 2x3 sliding puzzle, represented as a 2x3 array board. The board contains numbers 0 to 5. The number 0 represents the empty slot. You can move the numbers. When board becomes [[1,2,3],[4,5,0]], you win the game.

Write an algorithm to find the minimum number of moves to win the game. If it is impossible to win, return -1.

For example, if the input is board = [[4,1,2],[5,0,3]], the algorithm should return 5:

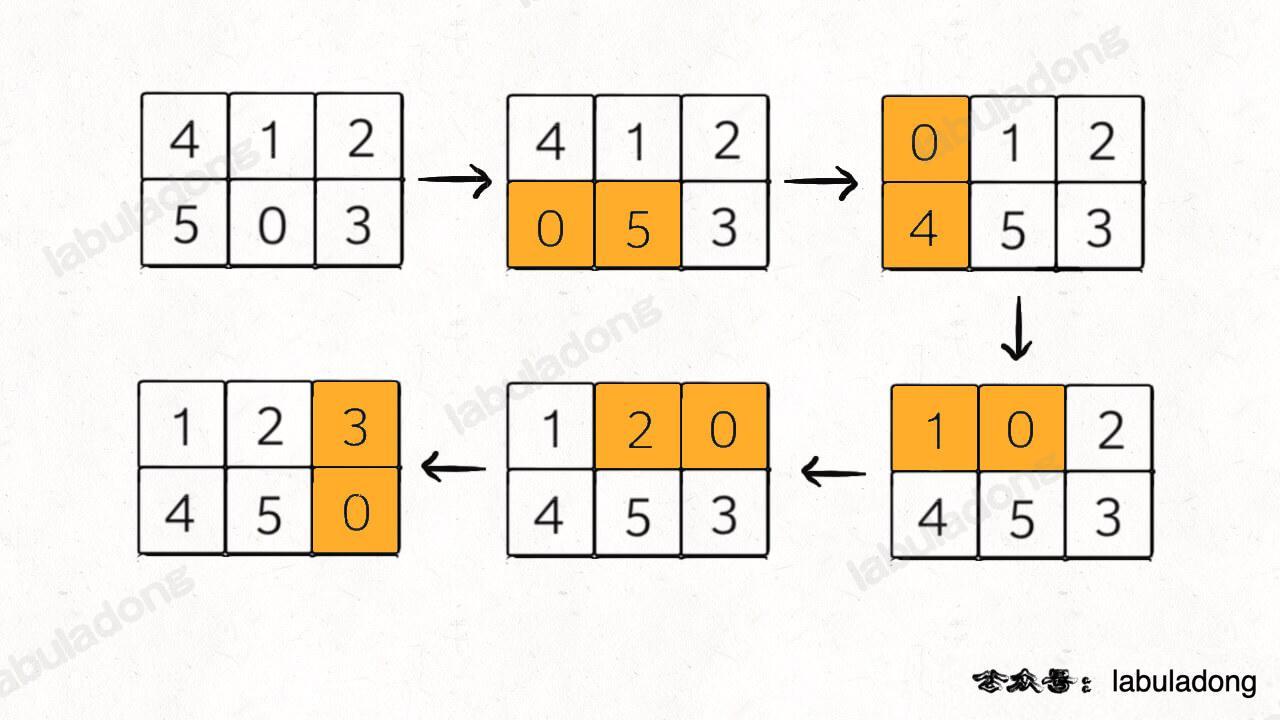
If the input is board = [[1,2,3],[5,4,0]], the algorithm should return -1 because there is no way to win from this situation.

This puzzle is quite interesting. I played similar games when I was young, such as the "Huarong Dao":

You need to move the blocks and try to move Cao Cao from the starting position to the exit at the bottom.

"Huarong Dao" is harder than this problem because the blocks have different sizes, while in this problem, each block has the same size.

Back to this problem, how do we change it into a tree or graph structure so we can use the BFS algorithm?

The initial state of the board is the starting point:

[[2,4,1],
 [5,0,3]]

Our goal is to turn the board into this:

[[1,2,3],
 [4,5,0]]

This is the target.

Now, this problem becomes a graph problem. The question is actually asking for the shortest path from the start to the target.

Who are the neighbors of the start? You can swap the 0 with the numbers above, below, left, or right. These are the neighbors of the start (since the board is 2x3, the actual neighbors are less than four if on the edge):

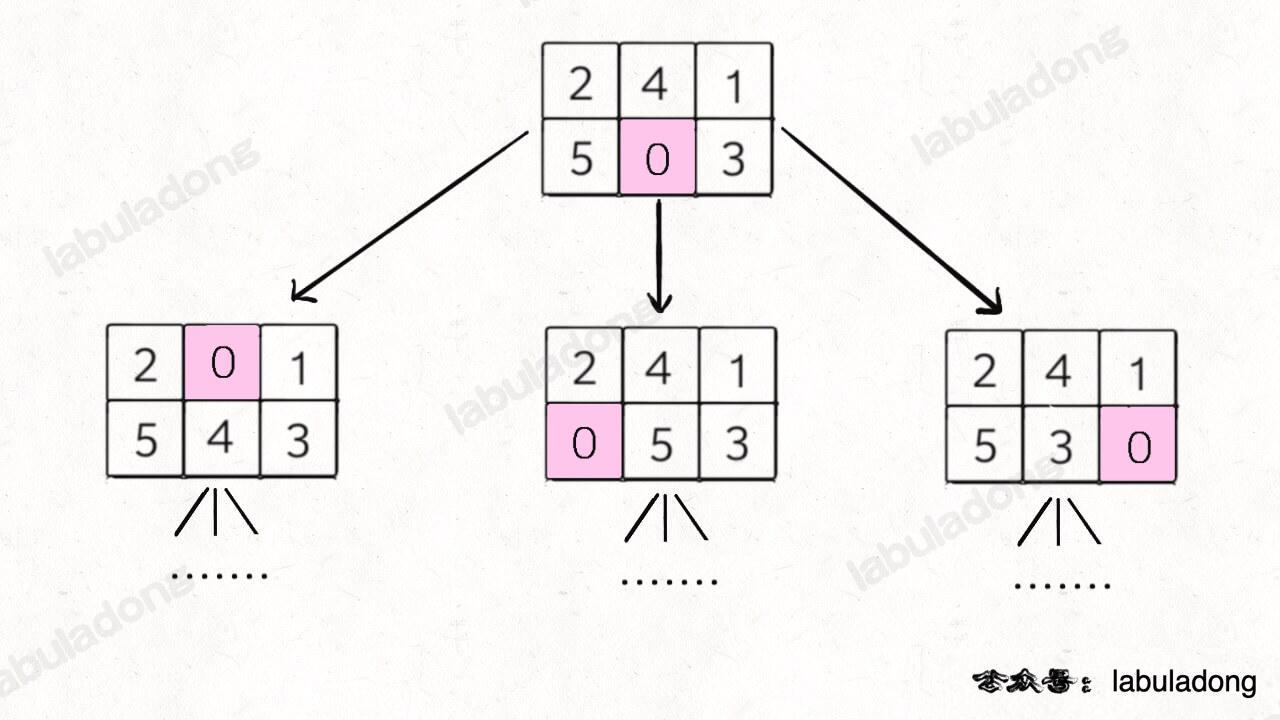
In the same way, each neighbor has its own neighbors. This makes a graph.

So, we can use BFS from the start. The first time we reach the target, the number of steps is the answer.

Here is the pseudocode:

int bfs(int[][] board, int[][] target) {
    Queue<int[][]> q = new LinkedList<>();
    HashSet visited = new HashSet<>();

    // add the start point to the queue
    q.offer(board);
    visited.add(board);

    int step = 0;
    while (!q.isEmpty()) {
        int sz = q.size();
        for (int i = 0; i < sz; i++) {
            int[][] cur = q.poll();
            // determine if the end point is reached
            if (cur == target) {
                return step;
            }
            // add the neighbors of the current node to the queue
            for (int[][] neighbor : getNeighbors(cur)) {
                if (!visited.contains(neighbor)) {
                    q.offer(neighbor);
                    visited.add(neighbor);
                }
            }
        }
        step++;
    }
    return -1;
}

List<int[][]> getNeighbors(int[][] board) {
    // swap the number 0 with the numbers above, below, left, and right, to get 4 neighbors
}

For this problem, the abstracted graph structure can also contain cycles, so we need a visited array to record the nodes we have already visited. This can prevent infinite loops caused by cycles.

For example, if we start from the node [[2,4,1],[5,0,3]], moving 0 to the right gives a new node [[2,4,1],[5,3,0]]. In this new node, 0 can move left again, returning to [[2,4,1],[5,0,3]]. This is a cycle. So we need a visited hash set to record the nodes we have visited and avoid infinite loops caused by cycles.

There is another problem. In this problem, board is a 2D array. As we explained in How Hash Set Works, a 2D array is a mutable data structure and cannot be directly added to a hash set.

So we need a small trick. We must convert the 2D array into an immutable type before putting it into the hash set. A common way is to serialize the 2D array into a string, and then store it in the hash set.

The tricky part is: a 2D array has the concept of "up, down, left, right". After changing it into a 1D string, how can we still swap 0 with its neighbors?

For this problem, the input array is always 2 x 3, so we can write out the mapping by hand:

java

// Record the adjacent indices of one-dimensional strings
int[][] neighbor = new int[][]{
    {1, 3},
    {0, 4, 2},
    {1, 5},
    {0, 4},
    {3, 1, 5},
    {4, 2}
};

cpp

// Record the adjacent indices of one-dimensional strings
int neighbor[6][3] = {
    {1, 3},
    {0, 4, 2},
    {1, 5},
    {0, 4},
    {3, 1, 5},
    {4, 2}
};

python

# Record the adjacent indices of a one-dimensional string
neighbor = [
    [1, 3],
    [0, 4, 2],
    [1, 5],
    [0, 4],
    [3, 1, 5],
    [4, 2]
]

// Record adjacent indices of one-dimensional strings
neighbor := [][]int{
    {1, 3},
    {0, 4, 2},
    {1, 5},
    {0, 4},
    {3, 1, 5},
    {4, 2},
}

javascript

// Record the adjacent indices of one-dimensional strings
var neighbor = [
    [1, 3],
    [0, 4, 2],
    [1, 5],
    [0, 4],
    [3, 1, 5],
    [4, 2]
];

This mapping means: in the 1D string, the adjacent indices for index i in the 2D array are neighbor[i]:

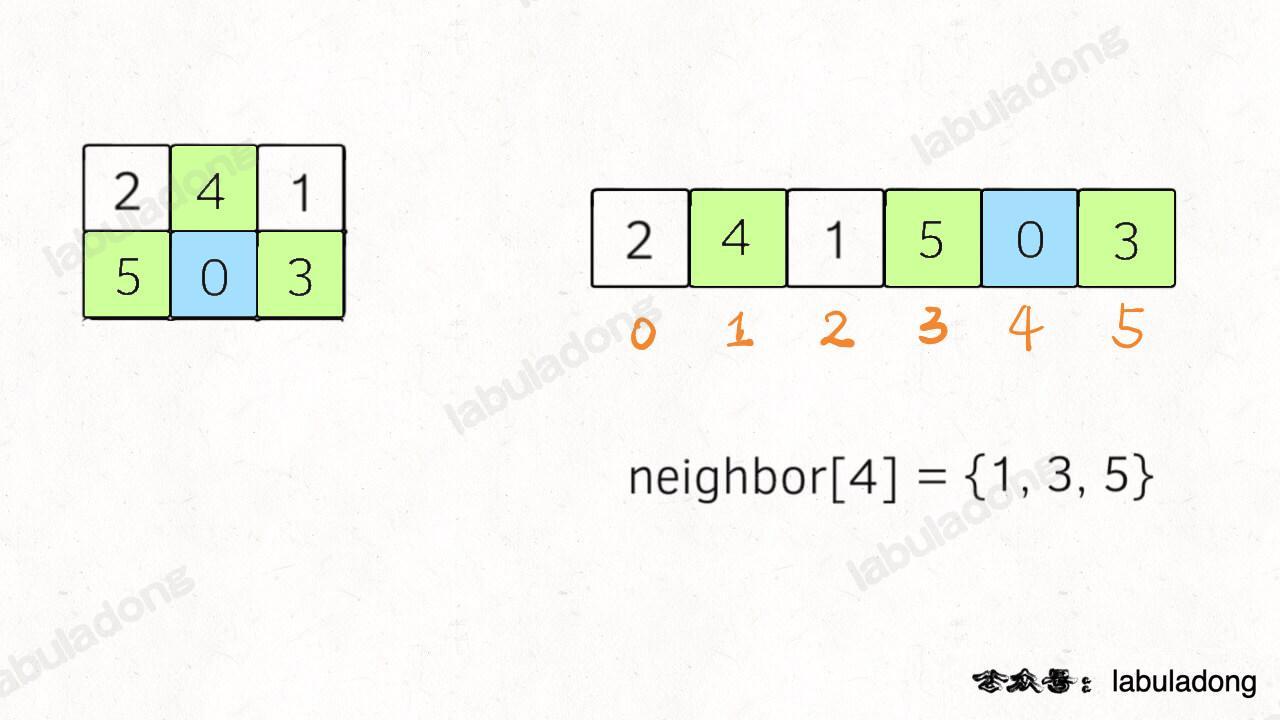
What if it is an m x n 2D array?

For an m x n 2D array, it's not practical to write the 1D mapping by hand. We need code to generate the neighbor mapping.

Look at the picture above. If an element e is at index i in the 1D array, then the left and right neighbors are at i - 1 and i + 1, and the up and down neighbors are at i - n and i + n, where n is the number of columns.

So for an m x n 2D array, we can write a function to generate the neighbor index mapping:

java

int[][] generateNeighborMapping(int m, int n) {
    int[][] neighbor = new int[m * n][];
    for (int i = 0; i < m * n; i++) {
        List<Integer> neighbors = new ArrayList<>();

        // if it is not the first column, it has a left neighbor
        if (i % n != 0) neighbors.add(i - 1);
        
        // if it is not the last column, it has a right neighbor
        if (i % n != n - 1) neighbors.add(i + 1);
        
        // if it is not the first row, it has an upper neighbor
        if (i - n >= 0) neighbors.add(i - n);
        
        // if it is not the last row, it has a lower neighbor
        if (i + n < m * n) neighbors.add(i + n);

        // Java language feature, convert List type to int[] array
        neighbor[i] = neighbors.stream().mapToInt(Integer::intValue).toArray();
    }
    return neighbor;
}

cpp

vector<vector<int>> generateNeighborMapping(int m, int n) {
    vector<vector<int>> neighbor(m * n);
    for (int i = 0; i < m * n; i++) {
        vector<int> neighbors;

        // if it's not the first column, it has a left neighbor
        if (i % n != 0) neighbors.push_back(i - 1);
        // if it's not the last column, it has a right neighbor
        if (i % n != n - 1) neighbors.push_back(i + 1);
        // if it's not the first row, it has an upper neighbor
        if (i - n >= 0) neighbors.push_back(i - n);
        // if it's not the last row, it has a lower neighbor
        if (i + n < m * n) neighbors.push_back(i + n);

        neighbor[i] = neighbors;
    }
    return neighbor;
}

python

def generateNeighborMapping(m: int, n: int) -> List[List[int]]:
    neighbor = [[] for _ in range(m * n)]
    for i in range(m * n):
        neighbors = []

        # if not the first column, it has a left neighbor
        if i % n != 0: neighbors.append(i - 1)
        
        # if not the last column, it has a right neighbor
        if i % n != n - 1: neighbors.append(i + 1)
        
        # if not the first row, it has an upper neighbor
        if i - n >= 0: neighbors.append(i - n)
        
        # if not the last row, it has a lower neighbor
        if i + n < m * n: neighbors.append(i + n)

        neighbor[i] = neighbors
    return neighbor

func generateNeighborMapping(m, n int) [][]int {
    neighbor := make([][]int, m*n)
    for i := 0; i < m*n; i++ {
        neighbors := make([]int, 0)

        // if it's not the first column, it has a left neighbor
        if i % n != 0 {
            neighbors = append(neighbors, i-1)
        }
        // if it's not the last column, it has a right neighbor
        if i % n != n-1 {
            neighbors = append(neighbors, i+1)
        }
        // if it's not the first row, it has an upper neighbor
        if i-n >= 0 {
            neighbors = append(neighbors, i-n)
        }
        // if it's not the last row, it has a lower neighbor
        if i+n < m*n {
            neighbors = append(neighbors, i+n)
        }

        neighbor[i] = neighbors
    }
    return neighbor
}

javascript

function generateNeighborMapping(m, n) {
    const neighbor = new Array(m * n).fill(0).map(() => []);
    for (let i = 0; i < m * n; i++) {
        const neighbors = [];

        // if not in the first column, has a left neighbor
        if (i % n !== 0) neighbors.push(i - 1);
        
        // if not in the last column, has a right neighbor
        if (i % n !== n - 1) neighbors.push(i + 1);
        
        // if not in the first row, has an upper neighbor
        if (i - n >= 0) neighbors.push(i - n);
        
        // if not in the last row, has a lower neighbor
        if (i + n < m * n) neighbors.push(i + n);

        neighbor[i] = neighbors;
    }
    return neighbor;
}

Now, no matter where 0 is, you can use the mapping to find its neighbors and swap. Here is the complete code:

java

class Solution {
    public int slidingPuzzle(int[][] board) {
        int m = 2, n = 3;
        StringBuilder sb = new StringBuilder();
        String target = "123450";
        // convert the 2x3 array into a string as the starting point for bfs
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                sb.append(board[i][j]);
            }
        }
        String start = sb.toString();

        // record the adjacent indices of the 1d string
        int[][] neighbor = new int[][]{
                {1, 3},
                {0, 4, 2},
                {1, 5},
                {0, 4},
                {3, 1, 5},
                {4, 2}
        };

        // ****** Start of BFS algorithm framework ******
        Queue<String> q = new LinkedList<>();
        HashSet<String> visited = new HashSet<>();
        // start bfs search from the starting point
        q.offer(start);
        visited.add(start);

        int step = 0;
        while (!q.isEmpty()) {
            int sz = q.size();
            for (int i = 0; i < sz; i++) {
                String cur = q.poll();
                // check if the target state is reached
                if (target.equals(cur)) {
                    return step;
                }
                // find the index of the number 0
                int idx = 0;
                for (; cur.charAt(idx) != '0'; idx++) ;
                // swap the number 0 with adjacent numbers
                for (int adj : neighbor[idx]) {
                    String new_board = swap(cur.toCharArray(), adj, idx);
                    // prevent revisiting the same state
                    if (!visited.contains(new_board)) {
                        q.offer(new_board);
                        visited.add(new_board);
                    }
                }
            }
            step++;
        }
        // ****** End of BFS algorithm framework ******
        return -1;
    }

    private String swap(char[] chars, int i, int j) {
        char temp = chars[i];
        chars[i] = chars[j];
        chars[j] = temp;
        return new String(chars);
    }

}

cpp

class Solution {
public:
    int slidingPuzzle(vector<vector<int>>& board) {
        string target = "123450";
        // convert the 2x3 array to a string as the starting point of BFS
        string start = "";
        for (int i = 0; i < board.size(); i++) {
            for (int j = 0; j < board[0].size(); j++) {
                start = start + to_string(board[i][j]);
            }
        }

        // ***** BFS algorithm framework starts *****
        queue<string> q;
        unordered_set<string> visited;
        // start BFS search from the starting point
        q.push(start);
        visited.insert(start);

        int step = 0;
        while (!q.empty()) {
            int sz = q.size();
            for (int i = 0; i < sz; i++) {
                string cur = q.front();
                q.pop();
                // determine if the target state is reached
                if (target == cur) {
                    return step;
                }
                // swap number 0 with its adjacent numbers
                for (string neighborBoard : getNeighbors(cur)) {
                    // prevent from going back
                    if (!visited.count(neighborBoard)) {
                        q.push(neighborBoard);
                        visited.insert(neighborBoard);
                    }
                }
            }
            step++;
        }
        // ***** BFS algorithm framework ends *****
        return -1;
    }

    vector<string> getNeighbors(string board) {
        // record the adjacent indices of the one-dimensional string
        vector<vector<int>> mapping = {
            {1, 3},
            {0, 4, 2},
            {1, 5},
            {0, 4},
            {3, 1, 5},
            {4, 2}
        };

        int idx = board.find('0');
        vector<string> neighbors;
        for (int adj : mapping[idx]) {
            string new_board = swap(board, idx, adj);
            neighbors.push_back(new_board);
        }
        return neighbors;
    }

    string swap(string board, int i, int j) {
        char temp = board[i];
        board[i] = board[j];
        board[j] = temp;
        return board;
    }
};

python

from collections import deque

class Solution:
    def slidingPuzzle(self, board):
        target = "123450"
        # convert the 2x3 array to a string as the starting point of BFS
        start = ""
        for i in range(len(board)):
            for j in range(len(board[0])):
                start += str(board[i][j])
        
        # ***** BFS algorithm framework starts *****
        q = deque()
        visited = set()
        # start BFS search from the starting point
        q.append(start)
        visited.add(start)
        
        step = 0
        while q: 
            # number of nodes in the current layer
            sz = len(q)
            for _ in range(sz):
                cur = q.popleft()
                # determine if the target state is reached
                if cur == target:
                    return step
                # swap number 0 with its adjacent numbers
                for neighbor_board in self.getNeighbors(cur):
                    # prevent from going back
                    if neighbor_board not in visited:
                        q.append(neighbor_board)
                        visited.add(neighbor_board)
            step += 1
        # ***** BFS algorithm framework ends *****
        return -1

    def getNeighbors(self, board):
        # record the adjacent indices of the one-dimensional string
        mapping = [
            [1, 3],
            [0, 4, 2],
            [1, 5],
            [0, 4],
            [3, 1, 5],
            [4, 2]
        ] 
        
        idx = board.index('0')
        neighbors = []
        for adj in mapping[idx]:
            new_board = self.swap(board, idx, adj)
            neighbors.append(new_board)
        return neighbors

    def swap(self, board, i, j):
        chars = list(board)
        chars[i], chars[j] = chars[j], chars[i]
        return ''.join(chars)

func slidingPuzzle(board [][]int) int {
    target := "123450"
    // convert the 2x3 array to a string as the starting point of BFS
    start := ""
    for i := 0; i < len(board); i++ {
        for j := 0; j < len(board[0]); j++ {
            start += string(rune(board[i][j] + '0'))
        }
    }

    // ***** BFS algorithm framework starts *****
    queue := []string{start}
    visited := make(map[string]bool)
    visited[start] = true

    step := 0
    for len(queue) > 0 {
        sz := len(queue)
        for i := 0; i < sz; i++ {
            cur := queue[0]
            queue = queue[1:]
            // determine if the target state is reached
            if cur == target {
                return step
            }
            // swap number 0 with its adjacent numbers
            for _, neighbor := range getNeighbors(cur) {
                // prevent from going back
                if !visited[neighbor] {
                    queue = append(queue, neighbor)
                    visited[neighbor] = true
                }
            }
        }
        step++
    }
    // ***** BFS algorithm framework ends *****
    return -1
}

func getNeighbors(board string) []string {
    // record the adjacent indices of the one-dimensional string
    mapping := [][]int{
        {1, 3},
        {0, 4, 2},
        {1, 5},
        {0, 4},
        {3, 1, 5},
        {4, 2},
    }

    idx := strings.Index(board, "0")
    neighbors := []string{}
    for _, adj := range mapping[idx] {
        newBoard := swap(board, idx, adj)
        neighbors = append(neighbors, newBoard)
    }
    return neighbors
}

func swap(board string, i, j int) string {
    chars := []rune(board)
    chars[i], chars[j] = chars[j], chars[i]
    return string(chars)
}

javascript

var slidingPuzzle = function(board) {
    const target = "123450";
    // convert the 2x3 array to a string as the starting point of BFS
    let start = "";
    for (let i = 0; i < board.length; i++) {
        for (let j = 0; j < board[0].length; j++) {
            start += board[i][j];
        }
    }

    // ***** BFS algorithm framework starts *****
    const queue = [start];
    const visited = new Set();
    visited.add(start);

    let step = 0;
    while (queue.length > 0) {
        const sz = queue.length;
        for (let i = 0; i < sz; i++) {
            const cur = queue.shift();
            // determine if the target state is reached
            if (cur === target) {
                return step;
            }
            // swap number 0 with its adjacent numbers
            for (const neighbor of getNeighbors(cur)) {
                // prevent from going back
                if (!visited.has(neighbor)) {
                    queue.push(neighbor);
                    visited.add(neighbor);
                }
            }
        }
        step++;
    }
    // ***** BFS algorithm framework ends *****
    return -1;
};

function getNeighbors(board) {
    // record the adjacent indices of the one-dimensional string
    const mapping = [
        [1, 3],
        [0, 4, 2],
        [1, 5],
        [0, 4],
        [3, 1, 5],
        [4, 2],
    ];

    const idx = board.indexOf('0');
    const neighbors = [];
    for (const adj of mapping[idx]) {
        const newBoard = swap(board, idx, adj);
        neighbors.push(newBoard);
    }
    return neighbors;
}

function swap(board, i, j) {
    const chars = board.split('');
    [chars[i], chars[j]] = [chars[j], chars[i]];
    return chars.join('');
}

Algorithm Visualization

This problem is solved. You can see the BFS algorithm itself is a fixed template. The hard part is changing the problem into the BFS model, and then using the right way to turn a multi-dimensional array into a string, so the hash set can record the visited nodes.

Let's look at another real-world problem.

Minimum Turns to Unlock the Lock

Let's look at LeetCode problem 752 "Open the Lock". It's an interesting problem:

752. Open the Lock | LeetCode | 🟠

You have a lock in front of you with 4 circular wheels. Each wheel has 10 slots: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9'. The wheels can rotate freely and wrap around: for example we can turn '9' to be '0', or '0' to be '9'. Each move consists of turning one wheel one slot.

The lock initially starts at '0000', a string representing the state of the 4 wheels.

You are given a list of deadends dead ends, meaning if the lock displays any of these codes, the wheels of the lock will stop turning and you will be unable to open it.

Given a target representing the value of the wheels that will unlock the lock, return the minimum total number of turns required to open the lock, or -1 if it is impossible.

Example 1:

Input: deadends = ["0201","0101","0102","1212","2002"], target = "0202"
Output: 6
Explanation: 
A sequence of valid moves would be "0000" -> "1000" -> "1100" -> "1200" -> "1201" -> "1202" -> "0202".
Note that a sequence like "0000" -> "0001" -> "0002" -> "0102" -> "0202" would be invalid,
because the wheels of the lock become stuck after the display becomes the dead end "0102".

Example 2:

Input: deadends = ["8888"], target = "0009"
Output: 1
Explanation: We can turn the last wheel in reverse to move from "0000" -> "0009".

Example 3:

Input: deadends = ["8887","8889","8878","8898","8788","8988","7888","9888"], target = "8888"
Output: -1
Explanation: We cannot reach the target without getting stuck.

Constraints:

1 <= deadends.length <= 500
deadends[i].length == 4
target.length == 4
target will not be in the list deadends.
target and deadends[i] consist of digits only.

The problem is from LeetCode 752. Open the Lock.

Here is the function signature:

java

class Solution {
    public int openLock(String[] deadends, String target) {
        // ...
    }
}

cpp

class Solution {
public:
    int openLock(vector<string>& deadends, string target) {
        // ...
    }
};

python

class Solution:
    def openLock(self, deadends: List[str], target: str) -> int:
        # ...

func openLock(deadends []string, target string) int {
    // ...
}

javascript

var openLock = function(deadends, target) {
    // ...
};

The problem describes a password lock that we often see in daily life. If there are no restrictions, it's easy to count the minimum number of turns. For example, if you want to reach "1234", you just turn each digit. The minimum turns will be 1 + 2 + 3 + 4 = 10.

But the difficulty is that you cannot go through any deadends while turning the lock. How do you handle deadends to make the total number of turns as few as possible?

Don't worry about the details or try to consider every specific case. Remember, the heart of algorithms is brute-force. We can simply try every possible turn from "0000". If we try all possible combinations, won't we definitely find the minimum turns?

First, ignore all restrictions like deadends and target. Think about this: if you need to write an algorithm to try all possible combinations, how would you do it?

Start from "0000". How many possibilities are there if you turn the lock once? There are 4 positions, and each can turn up or down. That is, you can get "1000", "9000", "0100", "0900"..., a total of 8 combinations.

Then, for each of these 8 combinations, you can turn again and get 8 more combinations for each, and so on...

Can you see the recursion tree? It is an 8-way tree, and each node has 8 children.

This pseudocode below describes this idea, using level-order traversal of an 8-way tree:

java

// increment s[j] by one
String plusOne(String s, int j) {
    char[] ch = s.toCharArray();
    if (ch[j] == '9')
        ch[j] = '0';
    else
        ch[j] += 1;
    return new String(ch);
}
// decrement s[j] by one
String minusOne(String s, int j) {
    char[] ch = s.toCharArray();
    if (ch[j] == '0')
        ch[j] = '9';
    else
        ch[j] -= 1;
    return new String(ch);
}

// BFS framework to find the minimum number of moves
void BFS(String target) {
    Queue<String> q = new LinkedList<>();
    q.offer("0000");

    int step = 0;

    while (!q.isEmpty()) {
        int sz = q.size();
        // spread all nodes in the current queue to their neighbors
        for (int i = 0; i < sz; i++) {
            String cur = q.poll();
            // determine if the end point is reached
            if (cur.equals(target)) {
                return step;
            }

            // a password can derive 8 neighboring passwords
            for (String neighbor : getNeighbors(cur)) {
                q.offer(neighbor);
            }
        }
        // increase the step count here
        step++;
    }
}
// increment or decrement each digit of s by one, return 8 neighboring passwords
List<String> getNeighbors(String s) {
    List<String> neighbors = new ArrayList<>();
    for (int i = 0; i < 4; i++) {
        neighbors.add(plusOne(s, i));
        neighbors.add(minusOne(s, i));
    }
    return neighbors;
}

cpp

// increment s[j] by one
string plusOne(string s, int j) {
    char ch[s.length()];
    strcpy(ch, s.c_str());
    if (ch[j] == '9')
        ch[j] = '0';
    else
        ch[j] += 1;
    string res(ch);
    return res;
}

// decrement s[i] by one
string minusOne(string s, int j) {
    char ch[s.length()];
    strcpy(ch, s.c_str());
    if (ch[j] == '0')
        ch[j] = '9';
    else
        ch[j] -= 1;
    string res(ch);
    return res;
}

// BFS framework to find the minimum number of moves
void BFS(string target) {
    queue<string> q;
    q.push("0000");
    
    while (!q.empty()) {
        int sz = q.size();
        // spread all nodes in the current queue
        for (int i = 0; i < sz; i++) {
            string cur = q.front(); q.pop();
            // determine if the end point is reached
            if (cur == target) {
                return step;
            }
            // a password can derive 8 neighboring passwords
            for (string neighbor : getNeighbors(cur)) {
                q.push(neighbor);
            }
        }
        // increment the step count here
        step++;
    }
    return -1;
}

// increment or decrement each digit of s by one, return 8 neighboring passwords
vector<string> getNeighbors(string s) {
    vector<string> neighbors;
    for (int i = 0; i < 4; i++) {
        neighbors.push_back(plusOne(s, i));
        neighbors.push_back(minusOne(s, i));
    }
    return neighbors;
}

python

from typing import List

# increment s[j] by one
def plusOne(s: str, j: int) -> str:
    ch = list(s)
    if ch[j] == '9':
        ch[j] = '0'
    else:
        ch[j] = chr(ord(ch[j]) + 1)
    return ''.join(ch)

# decrement s[j] by one
def minusOne(s: str, j: int) -> str:
    ch = list(s)
    if ch[j] == '0':
        ch[j] = '9'
    else:
        ch[j] = chr(ord(ch[j]) - 1)
    return ''.join(ch)

# BFS framework to find the minimum number of moves
def BFS(target: str) -> int:
    q = ['0000']
    
    while q:
        sz = len(q)
        # spread all nodes in the current queue to their surroundings
        for _ in range(sz):
            cur = q.pop(0)
            # determine if the end point is reached
            if cur == target:
                return step
            # add the neighbors of a node to the queue
            for neighbor in getNeighbors(cur):
                q.append(neighbor)
        # increment the step count here
        step += 1
    return -1

# increment or decrement each digit of s by one, return 8 neighboring passwords
def getNeighbors(s: str) -> List[str]:
    neighbors = []
    for i in range(4):
        neighbors.append(plusOne(s, i))
        neighbors.append(minusOne(s, i))
    return neighbors

// turn s[j] up by one
func plusOne(s string, j int) string {
    ch := []byte(s)
    if ch[j] == '9' {
        ch[j] = '0'
    } else {
        ch[j] += 1
    }
    return string(ch)
}

// turn s[i] down by one
func minusOne(s string, j int) string {
    ch := []byte(s)
    if ch[j] == '0' {
        ch[j] = '9'
    } else {
        ch[j] -= 1
    }
    return string(ch)
}

// BFS framework to find the minimum number of moves
func BFS(target string) int {
    q := []string{"0000"}
    step := 0

    for len(q) > 0 {
        sz := len(q)
        // spread all nodes in the current queue to their surroundings
        for i := 0; i < sz; i++ {
            cur := q[0]
            q = q[1:]
            // determine if the end point is reached
            if cur == target {
                return step
            }
            // add the neighbors of a node to the queue
            for _, neighbor := range getNeighbors(cur) {
                q = append(q, neighbor)
            }
        }
        // increment the step count here
        step++
    }
    return -1
}

// increment or decrement each digit of s by one, return 8 neighboring passwords
func getNeighbors(s string) []string {
    neighbors := []string{}
    for i := 0; i < 4; i++ {
        neighbors = append(neighbors, plusOne(s, i))
        neighbors = append(neighbors, minusOne(s, i))
    }
    return neighbors
}

javascript

// increment s[j] by one
var plusOne = function(s, j) {
    let ch = s.split('');
    if(ch[j] == '9') ch[j] = '0';
    else ch[j] = String.fromCharCode(ch[j].charCodeAt(0) + 1);
    return ch.join('');
};

// decrement s[i] by one
var minusOne = function(s, j) {
    let ch = s.split('');
    if(ch[j] == '0') ch[j] = '9';
    else ch[j] = String.fromCharCode(ch[j].charCodeAt(0) - 1);
    return ch.join('');
}

// BFS framework to find the minimum number of moves
var BFS = function(target) {
    let q = ['0000'];

    let step = 0;

    while(q.length > 0) {
        let sz = q.length;
        // spread all nodes in the current queue to their surroundings
        for(let i = 0; i < sz; i++) {
            let cur = q.shift();
            // determine if the end point is reached
            if(cur == target) {
                return step;
            }

            // add the neighbors of a node to the queue
            for(let neighbor of getNeighbors(cur)) {
                q.push(neighbor);
            }
        }
        // increment the step count here
        step++;
    }

    return -1;
}

// increment or decrement each digit of s by one, return 8 neighboring passwords
function getNeighbors(s) {
    let neighbors = [];
    for(let i = 0; i < 4; i++) {
        neighbors.push(plusOne(s, i));
        neighbors.push(minusOne(s, i));
    }
    return neighbors;
}

This code can already try all possible combinations, but there are still some problems to solve.

There will be repeated paths. For example, you can go from "0000" to "1000", but when you take "1000" from the queue, you can turn it back to "0000". This will create an infinite loop.

This is easy to fix. Actually, it is a cycle in the graph. We can use a visited set to record all passwords we have already tried. If you see the same password again, just don't add it to the queue.

We haven't handled deadends. We should avoid these "dead passwords".

This can also be fixed easily. Use a deadends set to record these passwords. Whenever you meet one, do not add it to the queue.

Or even simpler, just add all deadends to the visited set at the beginning. This works too.

Here is the complete code:

java

class Solution {
    public int openLock(String[] deadends, String target) {
        // record the deadends that need to be skipped
        Set<String> deads = new HashSet<>();
        for (String s : deadends) deads.add(s);
        if (deads.contains("0000")) return -1;

        // record the passwords that have been exhausted to prevent backtracking
        Set<String> visited = new HashSet<>();
        Queue<String> q = new LinkedList<>();
        // start breadth-first search from the starting point
        int step = 0;
        q.offer("0000");
        visited.add("0000");
        
        while (!q.isEmpty()) {
            int sz = q.size();
            // spread all nodes in the current queue to their surroundings
            for (int i = 0; i < sz; i++) {
                String cur = q.poll();
                
                // determine if the end is reached
                if (cur.equals(target))
                    return step;
                
                // add the valid adjacent nodes of a node to the queue
                for (String neighbor : getNeighbors(cur)) {
                    if (!visited.contains(neighbor) && !deads.contains(neighbor)) {
                        q.offer(neighbor);
                        visited.add(neighbor);
                    }
                }
            }
            // increment the step count here
            step++;
        }
        // if the target password is not found after exhaustion, then it is not found
        return -1;
    }

    // turn s[j] up once
    String plusOne(String s, int j) {
        char[] ch = s.toCharArray();
        if (ch[j] == '9')
            ch[j] = '0';
        else
            ch[j] += 1;
        return new String(ch);
    }

    // turn s[i] down once
    String minusOne(String s, int j) {
        char[] ch = s.toCharArray();
        if (ch[j] == '0')
            ch[j] = '9';
        else
            ch[j] -= 1;
        return new String(ch);
    }

    // increment or decrement each digit of s by one, return 8 neighboring passwords
    List<String> getNeighbors(String s) {
        List<String> neighbors = new ArrayList<>();
        for (int i = 0; i < 4; i++) {
            neighbors.add(plusOne(s, i));
            neighbors.add(minusOne(s, i));
        }
        return neighbors;
    }
}

cpp

class Solution {
public:
    int openLock(vector<string>& deadends, string target) {
        // record the deadends that need to be skipped
        unordered_set<string> deads(deadends.begin(), deadends.end());
        if (deads.count("0000")) return -1;

        // record the passwords that have been exhausted to prevent backtracking
        unordered_set<string> visited;
        queue<string> q;
        // start breadth-first search from the starting point
        int step = 0;
        q.push("0000");
        visited.insert("0000");
        
        while (!q.empty()) {
            int sz = q.size();
            // spread all nodes in the current queue to their surroundings
            for (int i = 0; i < sz; i++) {
                string cur = q.front();
                q.pop();
                
                // determine if the end is reached
                if (cur == target)
                    return step;
                
                // add the valid adjacent nodes of a node to the queue
                for (string neighbor : getNeighbors(cur)) {
                    if (!visited.count(neighbor) && !deads.count(neighbor)) {
                        q.push(neighbor);
                        visited.insert(neighbor);
                    }
                }
            }
            // increment the step count here
            step++;
        }
        // if the target password is not found after exhaustion, then it is not found
        return -1;
    }

    // turn s[j] up once
    string plusOne(string s, int j) {
        if (s[j] == '9')
            s[j] = '0';
        else
            s[j] += 1;
        return s;
    }

    // turn s[i] down once
    string minusOne(string s, int j) {
        if (s[j] == '0')
            s[j] = '9';
        else
            s[j] -= 1;
        return s;
    }

    // increment or decrement each digit of s by one, return 8 neighboring passwords
    vector<string> getNeighbors(string s) {
        vector<string> neighbors;
        for (int i = 0; i < 4; i++) {
            neighbors.push_back(plusOne(s, i));
            neighbors.push_back(minusOne(s, i));
        }
        return neighbors;
    }
};

python

class Solution:
    def openLock(self, deadends: List[str], target: str) -> int:
        # record the deadends that need to be skipped
        deads = set(deadends)
        if "0000" in deads:
            return -1

        # record the passwords that have been exhausted to prevent backtracking
        visited = set()
        q = collections.deque()
        # start breadth-first search from the starting point
        step = 0
        q.append("0000")
        visited.add("0000")
        
        while q:
            sz = len(q)
            # spread all nodes in the current queue to their surroundings
            for _ in range(sz):
                cur = q.popleft()
                
                # determine if the end is reached
                if cur == target:
                    return step
                
                # add the valid adjacent nodes of a node to the queue
                for neighbor in self.getNeighbors(cur):
                    if neighbor not in visited and neighbor not in deads:
                        q.append(neighbor)
                        visited.add(neighbor)
            
            # increment the step count here
            step += 1
        
        # if the target password is not found after exhaustion, then it is not found
        return -1

    # turn s[j] up once
    def plusOne(self, s: str, j: int) -> str:
        ch = list(s)
        if ch[j] == '9':
            ch[j] = '0'
        else:
            ch[j] = chr(ord(ch[j]) + 1)
        return ''.join(ch)

    # turn s[i] down once
    def minusOne(self, s: str, j: int) -> str:
        ch = list(s)
        if ch[j] == '0':
            ch[j] = '9'
        else:
            ch[j] = chr(ord(ch[j]) - 1)
        return ''.join(ch)

    # increment or decrement each digit of s by one, return 8 neighboring passwords
    def getNeighbors(self, s: str) -> List[str]:
        neighbors = []
        for i in range(4):
            neighbors.append(self.plusOne(s, i))
            neighbors.append(self.minusOne(s, i))
        return neighbors

func openLock(deadends []string, target string) int {
    // record the deadends that need to be skipped
    deads := make(map[string]struct{})
    for _, s := range deadends {
        deads[s] = struct{}{}
    }
    if _, found := deads["0000"]; found {
        return -1
    }

    // record the passwords that have been exhausted to prevent backtracking
    visited := make(map[string]struct{})
    q := make([]string, 0)
    // start breadth-first search from the starting point
    step := 0
    q = append(q, "0000")
    visited["0000"] = struct{}{}
    
    for len(q) > 0 {
        sz := len(q)
        // spread all nodes in the current queue to their surroundings
        for i := 0; i < sz; i++ {
            cur := q[0]
            q = q[1:]
            
            // determine if the end is reached
            if cur == target {
                return step
            }
            
            // add the valid adjacent nodes of a node to the queue
            for _, neighbor := range getNeighbors(cur) {
                if _, found := visited[neighbor]; !found {
                    if _, dead := deads[neighbor]; !dead {
                        q = append(q, neighbor)
                        visited[neighbor] = struct{}{}
                    }
                }
            }
        }
        // increment the step count here
        step++
    }
    // if the target password is not found after exhaustion, then it is not found
    return -1
}

// turn s[j] up once
func plusOne(s string, j int) string {
    ch := []rune(s)
    if ch[j] == '9' {
        ch[j] = '0'
    } else {
        ch[j]++
    }
    return string(ch)
}

// turn s[i] down once
func minusOne(s string, j int) string {
    ch := []rune(s)
    if ch[j] == '0' {
        ch[j] = '9'
    } else {
        ch[j]--
    }
    return string(ch)
}

// increment or decrement each digit of s by one, return 8 neighboring passwords
func getNeighbors(s string) []string {
    neighbors := make([]string, 0)
    for i := 0; i < 4; i++ {
        neighbors = append(neighbors, plusOne(s, i))
        neighbors = append(neighbors, minusOne(s, i))
    }
    return neighbors
}

javascript

var openLock = function(deadends, target) {
    // record the deadends that need to be skipped
    let deads = new Set(deadends);
    if (deads.has("0000")) return -1;

    // record the passwords that have been exhausted to prevent backtracking
    let visited = new Set();
    let q = [];
    // start breadth-first search from the starting point
    let step = 0;
    q.push("0000");
    visited.add("0000");
    
    while (q.length !== 0) {
        let sz = q.length;
        // spread all nodes in the current queue to their surroundings
        for (let i = 0; i < sz; i++) {
            let cur = q.shift();
            
            // determine if the end is reached
            if (cur === target)
                return step;
            
            // add the valid adjacent nodes of a node to the queue
            for (let neighbor of getNeighbors(cur)) {
                if (!visited.has(neighbor) && !deads.has(neighbor)) {
                    q.push(neighbor);
                    visited.add(neighbor);
                }
            }
        }
        // increment the step count here
        step++;
    }
    // if the target password is not found after exhaustion, then it is not found
    return -1;
};

// turn s[j] up once
var plusOne = function(s, j) {
    let ch = s.split('');
    if (ch[j] === '9')
        ch[j] = '0';
    else
        ch[j] = (parseInt(ch[j]) + 1).toString();
    return ch.join('');
};

// turn s[i] down once
var minusOne = function(s, j) {
    let ch = s.split('');
    if (ch[j] === '0')
        ch[j] = '9';
    else
        ch[j] = (parseInt(ch[j]) - 1).toString();
    return ch.join('');
};

// increment or decrement each digit of s by one, return 8 neighboring passwords
var getNeighbors = function(s) {
    let neighbors = [];
    for (let i = 0; i < 4; i++) {
        neighbors.push(plusOne(s, i));
        neighbors.push(minusOne(s, i));
    }
    return neighbors;
};

Bidirectional BFS Optimization

Now let's talk about an optimization for BFS called Bidirectional BFS. This method can make BFS faster.

Think of this technique as extra reading. In most interviews and tests, normal BFS is enough. Only consider bidirectional BFS when your solution is too slow or if the interviewer asks for more optimization.

Bidirectional BFS is an advanced version of standard BFS:

In normal BFS, you start from the starting point and search outwards until you find the target. In bidirectional BFS, you start searching from both the start and the end at the same time. When the two searches meet, you stop.

Why is this faster?

It's like person A is looking for person B. In normal BFS, A goes to find B while B stays in place. In bidirectional BFS, both A and B walk toward each other. Of course, they will meet faster this way.

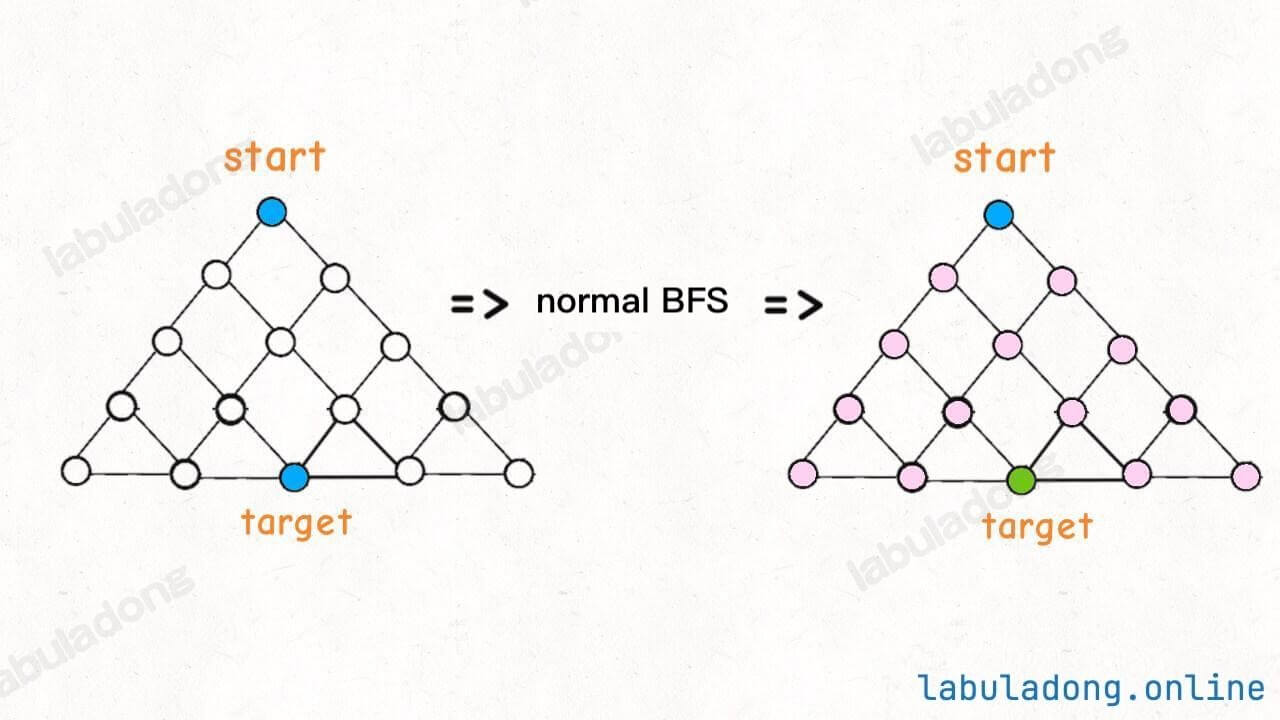
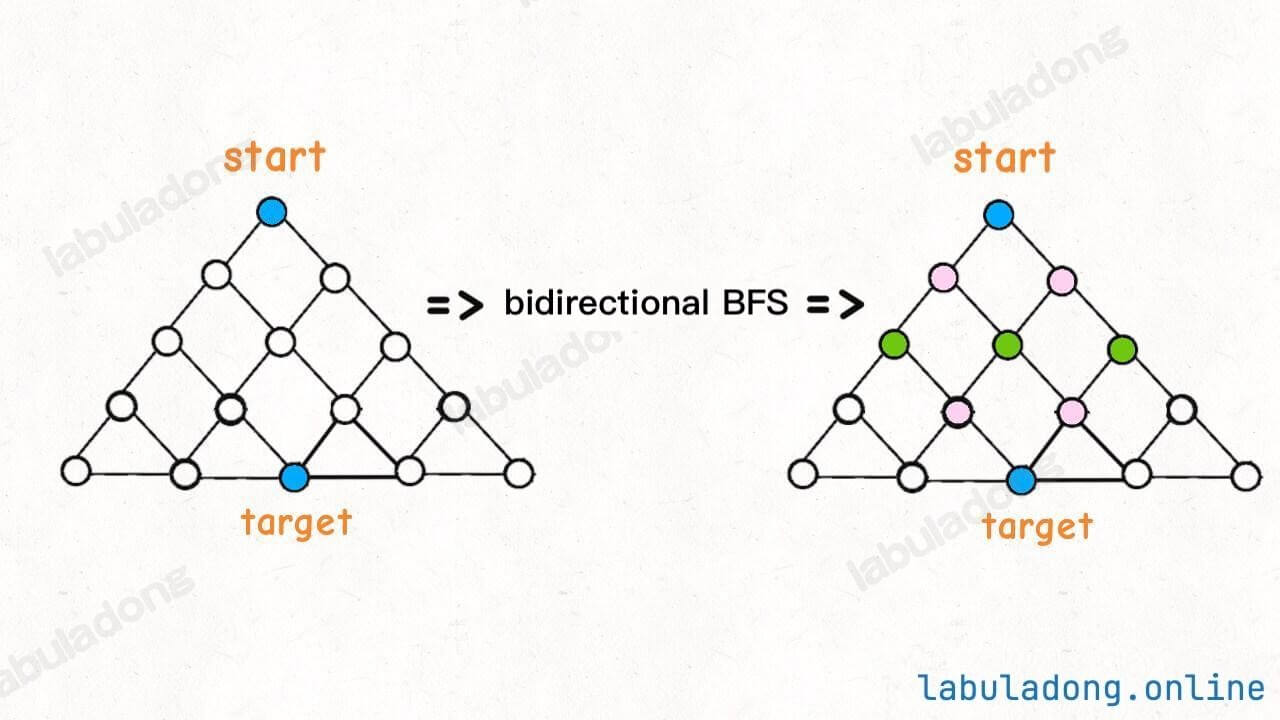
In the picture above, if the target is at the bottom of the tree, normal BFS will search the whole tree before finding the target. But bidirectional BFS only searches half the tree before the two searches meet, so it is faster.

From the Big O notation, both methods are $O(N)$ in the worst case, since both might search all nodes. But in real practice, bidirectional BFS is often much faster.

Limitations of Bidirectional BFS

You must know where the target is to use bidirectional BFS.

For BFS, you always know the start point. But sometimes you do not know the target node at the beginning.

For example, in the lock problem or the sliding puzzle problem above, the target is given, so you can use bidirectional BFS.

But in the Binary Tree DFS/BFS traversal, the start is the root, but the target is the nearest leaf, which you do not know at the start. So you can't use bidirectional BFS there.

Let's use the lock problem as an example to see how to upgrade BFS to bidirectional BFS. Here is the code:

java

class Solution {
    public int openLock(String[] deadends, String target) {
        Set<String> deads = new HashSet<>();
        for (String s : deadends) deads.add(s);
        // base case
        if (deads.contains("0000")) return -1;
        if (target.equals("0000")) return 0;

        // Use a set instead of a queue to quickly determine if an element exists
        Set<String> q1 = new HashSet<>();
        Set<String> q2 = new HashSet<>();
        Set<String> visited = new HashSet<>();
        
        int step = 0;
        q1.add("0000");
        visited.add("0000");
        q2.add(target);
        visited.add(target);

        while (!q1.isEmpty() && !q2.isEmpty()) {
            // Increment the step count here
            step++;

            // The hash set cannot be modified during traversal, so
            // use newQ1 to store the neighbor nodes
            Set<String> newQ1 = new HashSet<>();

            // Get the neighbors of all nodes in q1
            for (String cur : q1) {
                // Add an unvisited neighboring node of a node to the set
                for (String neighbor : getNeighbors(cur)) {
                    // Determine if the end point is reached
                    if (q2.contains(neighbor)) {
                        return step;
                    }
                    if (!visited.contains(neighbor) && !deads.contains(neighbor)) {
                        newQ1.add(neighbor);
                        visited.add(neighbor);
                    }
                }
            }
            // newQ1 stores the neighbors of q1
            q1 = newQ1;
            // Because each BFS spreads q1, the set with fewer elements is used as q1
            if (q1.size() > q2.size()) {
                Set<String> temp = q1;
                q1 = q2;
                q2 = temp;
            }
        }
        return -1;
    }

    // Turn s[j] up once
    String plusOne(String s, int j) {
        char[] ch = s.toCharArray();
        if (ch[j] == '9')
            ch[j] = '0';
        else
            ch[j] += 1;
        return new String(ch);
    }

    // Turn s[i] down once
    String minusOne(String s, int j) {
        char[] ch = s.toCharArray();
        if (ch[j] == '0')
            ch[j] = '9';
        else
            ch[j] -= 1;
        return new String(ch);
    }

    List<String> getNeighbors(String s) {
        List<String> neighbors = new ArrayList<>();
        for (int i = 0; i < 4; i++) {
            neighbors.add(plusOne(s, i));
            neighbors.add(minusOne(s, i));
        }
        return neighbors;
    }
}

cpp

class Solution {
public:
    int openLock(vector<string>& deadends, string target) {
        unordered_set<string> deads(deadends.begin(), deadends.end());
        
        // base case
        if (deads.count("0000")) return -1;
        if (target == "0000") return 0;

        // Use a set instead of a queue to quickly determine if an element exists
        unordered_set<string> q1;
        unordered_set<string> q2;
        unordered_set<string> visited;

        int step = 0;
        q1.insert("0000");
        visited.insert("0000");
        q2.insert(target);
        visited.insert(target);

        while (!q1.empty() && !q2.empty()) {

            // Increment the step count here
            step++;

            // The hash set cannot be modified during traversal, so
            // use newQ1 to store the neighbor nodes
            unordered_set<string> newQ1;

            // Get the neighbors of all nodes in q1
            for (const string& cur : q1) {
                // Add an unvisited neighboring node of a node to the set
                for (const string& neighbor : getNeighbors(cur)) {
                    // Determine if the end point is reached
                    if (q2.count(neighbor)) {
                        return step;
                    }
                    if (!visited.count(neighbor) && !deads.count(neighbor)) {
                        newQ1.insert(neighbor);
                        visited.insert(neighbor);
                    }
                }
            }
            // newQ1 stores the neighbors of q1
            q1 = newQ1;
            // Because each BFS spreads q1, the set with fewer elements is used as q1
            if (q1.size() > q2.size()) {
                swap(q1, q2);
            }
        }
        return -1;
    }

    // Turn s[j] up once
    string plusOne(string s, int j) {
        if (s[j] == '9')
            s[j] = '0';
        else
            s[j] += 1;
        return s;
    }

    // Turn s[i] down once
    string minusOne(string s, int j) {
        if (s[j] == '0')
            s[j] = '9';
        else
            s[j] -= 1;
        return s;
    }

    vector<string> getNeighbors(string s) {
        vector<string> neighbors;
        for (int i = 0; i < 4; i++) {
            neighbors.push_back(plusOne(s, i));
            neighbors.push_back(minusOne(s, i));
        }
        return neighbors;
    }
};

python

class Solution:
    def openLock(self, deadends: List[str], target: str) -> int:
        deads = set(deadends)
        # base case
        if "0000" in deads: return -1
        if target == "0000": return 0

        # Use a set instead of a queue to quickly determine if an element exists
        q1 = set()
        q2 = set()
        visited = set()
        
        step = 0
        q1.add("0000")
        visited.add("0000")
        q2.add(target)
        visited.add(target)

        while q1 and q2: 
            # Increment the step count here
            step += 1

            # The hash set cannot be modified during traversal,
            # so use newQ1 to store the neighbor nodes
            newQ1 = set()

            # Get the neighbors of all nodes in q1
            for cur in q1:
                # Add an unvisited neighboring node of a node to the set
                for neighbor in self.getNeighbors(cur):
                    # Determine if the end point is reached
                    if neighbor in q2:
                        return step
                    if neighbor not in visited and neighbor not in deads:
                        newQ1.add(neighbor)
                        visited.add(neighbor)
            # newQ1 stores the neighbors of q1
            q1 = newQ1
            # Because each BFS spreads q1, the set with fewer elements is used as q1
            if len(q1) > len(q2):
                q1, q2 = q2, q1
        return -1

    # Turn s[j] up once
    def plusOne(self, s: str, j: int) -> str:
        ch = list(s)
        if ch[j] == '9':
            ch[j] = '0'
        else:
            ch[j] = str(int(ch[j]) + 1)
        return ''.join(ch)

    # Turn s[i] down once
    def minusOne(self, s: str, j: int) -> str:
        ch = list(s)
        if ch[j] == '0':
            ch[j] = '9'
        else:
            ch[j] = str(int(ch[j]) - 1)
        return ''.join(ch)

    def getNeighbors(self, s: str) -> List[str]:
        neighbors = []
        for i in range(4):
            neighbors.append(self.plusOne(s, i))
            neighbors.append(self.minusOne(s, i))
        return neighbors

func openLock(deadends []string, target string) int {
    deads := make(map[string]struct{})
    for _, s := range deadends {
        deads[s] = struct{}{}
    }
    // base case
    if _, found := deads["0000"]; found {
        return -1
    }
    if target == "0000" {
        return 0
    }

    // Use a set instead of a queue to quickly determine if an element exists
    q1 := make(map[string]struct{})
    q2 := make(map[string]struct{})
    visited := make(map[string]struct{})

    step := 0
    q1["0000"] = struct{}{}
    visited["0000"] = struct{}{}
    q2[target] = struct{}{}
    visited[target] = struct{}{}

    for len(q1) != 0 && len(q2) != 0 {
        // Increment the step count here
        step++

        // The hash set cannot be modified during traversal,
        // so use newQ1 to store the neighbor nodes
        newQ1 := make(map[string]struct{})

        // Get the neighbors of all nodes in q1
        for cur := range q1 {
            // Add an unvisited neighboring node of a node to the set
            for _, neighbor := range getNeighbors(cur) {
                // Determine if the end point is reached
                if _, found := q2[neighbor]; found {
                    return step
                }
                if _, found := visited[neighbor]; !found {
                    if _, found := deads[neighbor]; !found {
                        newQ1[neighbor] = struct{}{}
                        visited[neighbor] = struct{}{}
                    }
                }
            }
        }
        // newQ1 stores the neighbors of q1
        q1 = newQ1
        // Because each BFS spreads q1, the set with fewer elements is used as q1
        if len(q1) > len(q2) {
            q1, q2 = q2, q1
        }
    }
    return -1
}

// Turn s[j] up once
func plusOne(s string, j int) string {
    ch := []rune(s)
    if ch[j] == '9' {
        ch[j] = '0'
    } else {
        ch[j]++
    }
    return string(ch)
}

// Turn s[i] down once
func minusOne(s string, j int) string {
    ch := []rune(s)
    if ch[j] == '0' {
        ch[j] = '9'
    } else {
        ch[j]--
    }
    return string(ch)
}

func getNeighbors(s string) []string {
    neighbors := []string{}
    for i := 0; i < 4; i++ {
        neighbors = append(neighbors, plusOne(s, i))
        neighbors = append(neighbors, minusOne(s, i))
    }
    return neighbors
}

javascript

var openLock = function(deadends, target) {
    let deads = new Set(deadends);
    // base case
    if (deads.has("0000")) return -1;
    if (target === "0000") return 0;

    // Use a set instead of a queue to quickly determine if an element exists
    let q1 = new Set();
    let q2 = new Set();
    let visited = new Set();

    let step = 0;
    q1.add("0000");
    visited.add("0000");
    q2.add(target);
    visited.add(target);

    while (q1.size && q2.size) {
        // Increment the step count here
        step++;

        // The hash set cannot be modified during traversal,
        // so use newQ1 to store the neighbor nodes
        let newQ1 = new Set();

        // Get the neighbors of all nodes in q1
        for (let cur of q1) {
            // Add an unvisited neighboring node of a node to the set
            for (let neighbor of getNeighbors(cur)) {
                // Determine if the end point is reached
                if (q2.has(neighbor)) {
                    return step;
                }
                if (!visited.has(neighbor) && !deads.has(neighbor)) {
                    newQ1.add(neighbor);
                    visited.add(neighbor);
                }
            }
        }
        // newQ1 stores the neighbors of q1
        q1 = newQ1;
        // Because each BFS spreads q1, the set with fewer elements is used as q1
        if (q1.size > q2.size) {
            let temp = q1;
            q1 = q2;
            q2 = temp;
        }
    }
    return -1;
};

// Turn s[j] up once
function plusOne(s, j) {
    let ch = s.split('');
    if (ch[j] === '9')
        ch[j] = '0';
    else
        ch[j] = (parseInt(ch[j]) + 1).toString();
    return ch.join('');
}

// Turn s[i] down once
function minusOne(s, j) {
    let ch = s.split('');
    if (ch[j] === '0')
        ch[j] = '9';
    else
        ch[j] = (parseInt(ch[j]) - 1).toString();
    return ch.join('');
}

function getNeighbors(s) {
    let neighbors = [];
    for (let i = 0; i < 4; i++) {
        neighbors.push(plusOne(s, i));
        neighbors.push(minusOne(s, i));
    }
    return neighbors;
}

Bidirectional BFS still follows the BFS framework, but there are a few differences:

Instead of using a queue, use a hash set to store elements. This makes it easier and faster to check if two sets have any common elements.
The place to return step is changed. In bidirectional BFS, you do not just check if you reached the end. Instead, you check if the two sets have common elements as soon as you find neighbors.
Another tip is to always make q1 the smaller set each time you search. This helps reduce the search size.

In BFS, the more elements in your queue (or set), the more neighbors you will add in the next round. In bidirectional BFS, if you always expand the smaller set, the total number of nodes searched grows more slowly and makes the algorithm faster.

Again, no matter if you use normal BFS or bidirectional BFS, and no matter if you optimize or not, the Big O time complexity is the same. Bidirectional BFS is just an advanced trick to speed up code in practice. It's not required.

The most important thing is to remember the general BFS framework and practice using it. Later, there is a BFS Exercise Section. Try to use the tips from this article to solve those problems.

Related Problems

You can install my Chrome extension then open the link.

LeetCode	Difficulty
1091. Shortest Path in Binary Matrix	🟠
111. Minimum Depth of Binary Tree	🟢
117. Populating Next Right Pointers in Each Node II	🟠
127. Word Ladder	🔴
1926. Nearest Exit from Entrance in Maze	🟠
2850. Minimum Moves to Spread Stones Over Grid	🟠
286. Walls and Gates🔒	🟠
310. Minimum Height Trees	🟠
329. Longest Increasing Path in a Matrix	🔴
365. Water and Jug Problem	🟠
431. Encode N-ary Tree to Binary Tree🔒	🔴
433. Minimum Genetic Mutation	🟠
490. The Maze🔒	🟠
505. The Maze II🔒	🟠
542. 01 Matrix	🟠
547. Number of Provinces	🟠
863. All Nodes Distance K in Binary Tree	🟠
994. Rotting Oranges	🟠

BFS Algorithm Common Patterns and Code Template

752. Open the Lock https://leetcode.com/problems/open-the-lock

773. Sliding Puzzle https://leetcode.com/problems/sliding-puzzle

Algorithm Framework

Sliding Puzzle

Minimum Turns to Unlock the Lock

Bidirectional BFS Optimization