How to Think About Data Structure and Algorithm

This article provides an overview of all the content on this site in two main parts: first, my understanding of the essence of data structures and algorithms; second, a summary of commonly used algorithms.

There is no complex code in this article. It is based on my experience and will help you avoid detours and deeply understand and master algorithms.

Summary of All Data Structures and Algorithms

All data structures are essentially transformations of arrays (sequential storage) and linked lists (linked storage).

The key point of data structures is in traversal and access, including basic operations such as adding, deleting, searching, and updating.

All algorithms are essentially brute-force.

The key to brute-force is no omission and no redundancy. Mastering algorithm frameworks allows for no omission; making full use of information ensures no redundancy.

If you truly understand the sentences above, you would not need to read the 7,000 words in this article, nor the dozens of algorithm tutorials and exercises on this site.

If you do not understand, then I will use the following thousands of words, as well as the upcoming articles and exercises, to explain these two sentences. While learning, always keep these two sentences in mind—they will greatly improve your learning efficiency.

Storage Methods of Data Structures

There are only two storage methods for data structures: Array (Sequential Storage) and Linked List (Linked Storage).

How should we understand this statement? Aren't there other data structures such as hash tables, stacks, queues, heaps, trees, graphs, etc.?

When analyzing issues, it's essential to have a recursive mindset, moving from the top down, from abstraction to concreteness. Listing many structures at the start overlooks that these belong to higher-level constructs, whereas arrays and linked lists form the foundational structure. All those diverse data structures ultimately originate from special operations on linked lists or arrays, differing only in their APIs.

For example, queues and stacks can be implemented using either linked lists or arrays. When using arrays, one must handle the issues of resizing; linked lists do not have this problem but require more memory space to store node pointers.

The two storage methods for graph structures are adjacency lists and adjacency matrices. An adjacency list is a linked list, while an adjacency matrix is a two-dimensional array. Adjacency matrices quickly determine connectivity and allow matrix operations to solve certain problems, but are space-consuming for sparse graphs. Adjacency lists save space, though many operations are less efficient than with adjacency matrices.

A hash table maps keys to a large array using a hash function. To resolve hash collisions, the chaining method uses linked list characteristics, which simplifies operations but requires extra space for pointers; the linear probing method utilizes array characteristics for continuous addressing, eliminating the need for pointer storage, but the operations are slightly more complex.

In tree structures, using an array results in a "heap" since a heap is a complete binary tree, and storing it in an array requires no node pointers, simplifying operations. A classic example is binary heap. Using linked lists results in the common "tree," which is unsuitable for array storage as it may not be a complete binary tree. Therefore, various ingenious designs are derived from this linked list "tree" structure to tackle different problems, such as binary search trees, AVL trees, red-black trees, interval trees, B-trees, and more.

In summary, there are many types of data structures, and you can even invent your own. However, the underlying storage is either arrays or linked lists. Their advantages and disadvantages are as follows:

Array is compactly and continuously stored, allowing random access and quick retrieval of elements via indexing while relatively conserving storage space. However, due to continuous storage, memory space must be allocated in one go, so resizing an array requires reallocating a larger space and copying all data, leading to a time complexity of O(N). Moreover, to insert or delete elements in the middle of an array, all subsequent data must be shifted to maintain continuity, resulting in a time complexity of $O(N)$.

Linked List elements are not continuous but are connected via pointers to the next element's location, avoiding the resizing issues of arrays. If the predecessor and successor of an element are known, the element can be deleted or a new one inserted by manipulating pointers, with a time complexity of $O(1)$. However, due to non-continuous storage space, the corresponding element's address cannot be calculated from an index, prohibiting random access. Each element must store pointers to adjacent elements, consuming relatively more storage space.

Basic Operations of Data Structures

For any data structure, the basic operations are traversal and access. More specifically, they are: insert, delete, search, and update.

There are many kinds of data structures. Their purpose is to perform insert, delete, search, and update as efficiently as possible in different situations. This is the mission of data structures.

How do we traverse and access? From a high level, there are only two types of traversal for all data structures: linear and nonlinear.

Linear traversal is usually done with for/while loops. Nonlinear traversal is usually done with recursion. More specifically, there are a few basic frameworks:

Array traversal framework, which is a typical linear iteration:

void traverse(int[] arr) {
    for (int i = 0; i < arr.length; i++) {
        // iterate through arr[i]
    }
}

void traverse(vector<int>& arr) {
    for (int i = 0; i < arr.size(); i++) {
        // iteratively access arr[i]
    }
}

def traverse(arr: List[int]):
    for i in range(len(arr)):
        # iterate over arr[i]

func traverse(arr []int) {
    for i := 0; i < len(arr); i++ {
        // iterate and access arr[i]
    }
}

var traverse = function(arr) {
  for (var i = 0; i < arr.length; i++) {
    // iterate and access arr[i]
  }
}

Linked list traversal framework, which can be both iterative and recursive:

// basic singly linked list node
class ListNode {
    int val;
    ListNode next;
}

void traverse(ListNode head) {
    for (ListNode p = head; p != null; p = p.next) {
        // iteratively access p.val
    }
}

void traverse(ListNode head) {
    // recursively access head.val
    traverse(head.next);
}

// basic singly-linked list node
class ListNode {
    public:
        int val;
        ListNode* next;
};

void traverse(ListNode* head) {
    for (ListNode* p = head; p != nullptr; p = p->next) {
        // iteratively access p->val
    }
}

void traverse(ListNode* head) {
    // recursively access head->val
    traverse(head->next);
}

# basic single linked list node
class ListNode:
    def __init__(self, val):
        self.val = val
        self.next = None

def traverse(head: ListNode) -> None:
    p = head
    while p is not None:
        # iteratively access p.val
        p = p.next

def traverse(head: ListNode) -> None:
    # recursively access head.val
    traverse(head.next)

// basic singly linked list node
type ListNode struct {
    val int
    next *ListNode
}

func traverse(head *ListNode) {
    for p := head; p != nil; p = p.next {
        // iteratively access p.val
    }
}

func traverse(head *ListNode) {
    // recursively access head.val
    traverse(head.next)
}

// basic single linked list node
class ListNode {
    constructor(val) {
        this.val = val;
        this.next = null;
    }
}

function traverse(head) {
    for (var p = head; p != null; p = p.next) {
        // iteratively access p.val
    }
}

function traverse(head) {
    // recursively access head.val
    traverse(head.next);
}

Binary tree traversal framework, which is a typical nonlinear recursive traversal:

// basic binary tree node
class TreeNode {
    int val;
    TreeNode left, right;
}

void traverse(TreeNode root) {
    traverse(root.left);
    traverse(root.right);
}

// basic binary tree node
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
};

void traverse(TreeNode* root) {
    traverse(root->left);
    traverse(root->right);
}

# basic binary tree node
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
        
def traverse(root: TreeNode):
    traverse(root.left)
    traverse(root.right)

// basic binary tree node
type TreeNode struct {
    val int
    left *TreeNode
    right *TreeNode
}

// post-order traversal of binary tree
func traverse(root *TreeNode) {
    if root != nil {
        traverse(root.left)
        traverse(root.right)
    }
}

// basic binary tree node
class TreeNode {
  constructor(val) {
    this.val = val;
    this.left = null;
    this.right = null;
  }
}

var traverse = function(root) {
  if (root === null) return;
  traverse(root.left);
  traverse(root.right);
};

Do you see the similarity between recursive traversal of binary trees and linked lists? Do you see how binary tree structure is similar to singly linked list structure? If you add more branches, can you traverse an N-ary tree?

The binary tree framework can be expanded to an N-ary tree traversal framework:

// basic N-ary tree node
class TreeNode {
    int val;
    TreeNode[] children;
}

void traverse(TreeNode root) {
    for (TreeNode child : root.children)
        traverse(child);
}

// basic N-ary tree node
class TreeNode {
public:
    int val;
    vector<TreeNode*> children;
};

void traverse(TreeNode* root) {
    for (TreeNode* child : root->children)
        traverse(child);
}

# basic N-ary tree node
class TreeNode:
    val: int
    children: List[TreeNode]

def traverse(root: TreeNode) -> None:
    for child in root.children:
        traverse(child)

// basic N-ary tree node
type TreeNode struct {
    val int
    children []*TreeNode
}

func traverse(root *TreeNode) {
    for _, child := range root.children {
        traverse(child)
    }
}

// basic N-ary tree node
var TreeNode = function(val, children) {
  this.val = val;
  this.children = children;
};

// traverse N-ary tree
var traverse = function(root) {
  for (var i = 0; i < root.children.length; i++) {
    traverse(root.children[i]);
  }
};

N-ary tree traversal can also be extended to graph traversal, because a graph is like a group of N-ary trees connected together. Worried about cycles in graphs? This is easy. Just use a boolean array called visited to mark nodes. For details, check Graph Traversal.

A framework is a template. No matter if you are inserting, deleting, searching, or updating, you always use these structures. You can treat the framework as an outline and add your code to it depending on the problem.

The Essence of Algorithms

If I had to sum up algorithms in one sentence, I would say: the essence of algorithms is "brute-force".

Some people might disagree. Are all algorithm problems really about brute-force? Aren’t there exceptions?

Of course, there are exceptions. For example, Some Problems You Can Solve in One Line of Code. These problems are like brain teasers. You need to observe, find patterns, and then get the best solution. But such problems are rare, so you don’t need to worry about them. Also, algorithms in cryptography or machine learning are not brute-force. They are based on math principles, so their essence is mathematics. They are not what we discuss in data structures and algorithms.

By the way, the "algorithm" that an algorithm engineer does is very different from the "algorithm" in data structures and algorithms. I want to make this clear, so beginners do not get confused.

For an algorithm engineer, the focus is on math modeling and tuning parameters. The computer is just a tool to do calculations. But for us, the focus is on computer thinking. You need to look at problems from a computer’s point of view, make them abstract and simple, and then use good data structures to solve them.

So, do not think that learning data structures and algorithms will make you an algorithm engineer. Also, do not think that if you are not going to be an algorithm engineer, you do not need to learn data structures and algorithms.

To be honest, most software jobs use existing frameworks and rarely touch low-level data structure and algorithm problems. But, if you want any tech-related job, you can’t escape data structure and algorithm questions. This knowledge is basic for programmers.

To make it clear, let’s call the algorithms in algorithm engineering "mathematical algorithms", and the algorithms for coding interviews "computer algorithms". What I write about focuses on "computer algorithms".

I hope this makes things clear. I guess most people’s goal is to pass algorithm tests and get a developer job. For that, you don’t need much math. You just need to learn how to use computer thinking to solve problems.

Computer thinking is not hard. Think about what a computer is good at. It is fast! Your brain can only think a few steps per second, but a CPU can do thousands or millions. So the computer’s way to solve problems is simple: brute-force.

When I started learning, I also thought algorithms were something very high-level. When I saw a problem, I wanted to find a math formula to get the answer quickly.

For example, if you tell someone who doesn’t know algorithms that you wrote an algorithm for permutations and combinations, they might think you invented a formula to give all answers. But the truth is, there is no fancy formula. I will explain this in Backtracking Kills Permutations and Combinations Problems. Actually, you just turn all possible combinations into a tree, and your code goes through this tree and collects all answers. That’s all. Nothing magical.

Maybe we misunderstand computer algorithms because of math classes. In math, you solve problems by observing, finding relationships, writing equations, and then getting the answer. If you try to brute-force in math, you probably have the wrong approach.

But computer thinking is the opposite. If there is a clever formula, that’s great. But if not, just brute-force! As long as the complexity is okay, brute-force will always find the answer. Theoretically, if you keep shuffling an array, one day it will be sorted! Of course, this is not a good algorithm, because who knows how long it will take.

In coding interviews, problems usually ask you to find the maximum or minimum. How do you do it? Just brute-force all possible answers and pick the best one. That’s all there is to it.

Difficulties of Brute-Force

How to Do Brute-Force

What kind of problems are hard because of "how to do brute-force"? Usually recursive problems, like backtracking or dynamic programming.

Let's start with backtracking. For example, when we learned permutations and combinations in high school, we could write them out by hand: pick the first position, then see all the choices for the second position, and so on. But, if you have not practiced, it is hard to turn this manual process into code. It is hard to find the pattern and write a program that tries all possibilities.

First, you need to think of permutations and combinations as a tree. Then, you need to use code to traverse all the nodes of the tree, not missing any, and not repeating. Only then will your code be correct. In later sections, I will introduce the core framework of backtracking, and then in backtracking to solve subsets, permutations, and combinations, I will show how to solve all these problems at once.

Dynamic programming is a bit harder than backtracking. Both are brute-force at heart, but the thinking is different. Backtracking is about "traversal", while dynamic programming is about "problem decomposition".

Now you can see why I say the hard part of dynamic programming is "how to do brute-force". Most people do not think about problems this way, but this thinking, combined with computers, is very powerful. So you need to practice. If you practice well, you can write algorithms easily and correctly.

In the core framework of dynamic programming, I explained how to solve dynamic programming problems. First, write the brute-force solution (the state transition equation). Then, add a memoization table and you have a top-down recursive solution. Change it a bit, and you get a bottom-up iterative solution. In dimension reduction in dynamic programming, I also talked about how to use space compression to make your code faster.

Adding memoization and space compression are standard tricks, not the hard part. When you do dynamic programming problems, you will find you often cannot even write the brute-force solution. You cannot find the state transition equation. So, finding the state transition equation (how to do brute-force) is the hard part.

I wrote a special article, Dynamic Programming Design: Mathematical Induction, to show you that the core of brute-force is mathematical induction. You need to clearly define the function, break down the problem, and then use this definition to solve subproblems with recursion.

How to Do Smart Brute-Force

What kind of algorithms focus on "how to do smart brute-force"? Many well-known non-recursive algorithm skills belong to this category.

The simplest example is searching for an element in a sorted array. Anyone can use a for loop to brute-force search, but the binary search algorithm is a smarter way to search, with better time complexity.

Another example is the Union Find algorithm mentioned before. It gives you a smart way to find connected components. In theory, to check whether two nodes in a graph are connected, you could use DFS or BFS to brute-force search. But the Union Find algorithm uses arrays to simulate tree structures, making the operation complexity for checking connections $O(1)$.

These are examples of smart brute-force. Experts invented these tricks. If you learn them, you can use them. If you haven't learned them, it's hard to come up with such ideas on your own.

Another example is the greedy algorithm. In Learning Greedy Algorithms, I said that greedy algorithms use patterns (called the greedy choice property) so that you don't need to brute-force all possible answers, but can still find the answer.

Dynamic programming at least tries all possible answers in a smart way to find the best one. But greedy algorithms sometimes do not need to try all solutions and can still find the answer, so in Greedy Algorithm for Jump Game, the greedy approach is even faster than dynamic programming. Of course, not every problem has the greedy choice property. That's why brute-force is simple and boring, but it always works when nothing else does.

Below, I list some common algorithm skills for you to learn and refer to.

Array/Singly Linked List Series Algorithms

A common technique for singly linked lists is the two-pointer method, which falls under the category of "smart brute-force". Summary of Two-Pointer Techniques for Singly Linked Lists provides a complete overview. For those who understand, it's easy; for those who don't, it's challenging.

For example, to determine if a singly linked list has a cycle, the brute-force method would involve using a data structure like a HashSet to store visited nodes, identifying a cycle when a duplicate is found. However, using fast and slow pointers can avoid additional space usage, which is a smarter brute-force approach.

Common techniques for arrays also involve the two-pointer method, which is part of "smart brute-force". Summary of Two-Pointer Techniques for Arrays covers everything. For those who understand, it's easy; for those who don't, it's challenging.

Firstly, the binary search technique can be categorized as two pointers moving from both ends to the center. If tasked with searching for an element in an array, a for loop with $O(N)$ time complexity can certainly accomplish the task. However, binary search shows that if the array is sorted, it only requires $O(logN)$ complexity, which is a smarter search method.

Detailed Framework of Binary Search provides a code template to ensure no boundary issues arise. Application of Binary Search Algorithms summarizes commonalities in binary search-related problems and how to apply the binary search concept to real-world algorithms.

Next, the Sliding Window Algorithm Technique is a typical fast and slow pointer method. Using nested for loops with $O(N^2)$ time complexity will certainly enumerate all subarrays and find those that meet the requirements. However, the sliding window algorithm demonstrates that in certain scenarios, using two pointers, one fast and one slow, only $O(N)$ time is needed to find the answer, which is a smarter brute-force approach.

Detailed Framework of Sliding Window Algorithm introduces applicable scenarios and a general code template for sliding window algorithms, ensuring you write correct code. Sliding Window Exercises guides you step by step to solve various problems using the sliding window framework.

Finally, the Prefix Sum Technique and Difference Array Technique.

If frequently required to calculate the sum of subarrays, using a for loop each time is feasible, but the prefix sum technique precomputes a preSum array to avoid loops.

Similarly, if frequently required to perform increment and decrement operations on subarrays, using a for loop each time is feasible, but the difference array technique maintains a diff array to avoid loops.

These are the main techniques for arrays and linked lists, which are relatively fixed. Once you've encountered them, applying them isn't too difficult. Let's move on to some slightly more challenging algorithms.

Binary Tree Algorithms

Old readers know that I always say how important binary trees are. The binary tree model is the foundation of many advanced algorithms. Many people have trouble understanding recursion, so it's best to practice binary tree problems.

As mentioned in Binary Tree Mindset (Summary), there are two main ideas for solving binary tree problems with recursion. The first is to traverse the binary tree to get the answer. The second is to break down the problem and calculate the answer. These two methods correspond to Backtracking Framework and Dynamic Programming Framework.

Traversal Thinking Pattern

What does it mean to get the answer by traversing the binary tree?

For example, to find the maximum depth of a binary tree, you need to write a function maxDepth. You can write code like this:

class Solution {

    // record the maximum depth
    int res = 0;
    // record the depth of the current node being traversed
    int depth = 0;

    // main function
    int maxDepth(TreeNode root) {
        traverse(root);
        return res;
    }

    // binary tree traversal framework
    void traverse(TreeNode root) {
        if (root == null) {
            // reach a leaf node
            res = Math.max(res, depth);
            return;
        }
        // pre-order traversal position
        depth++;
        traverse(root.left);
        traverse(root.right);
        // post-order traversal position
        depth--;
    }
}

class Solution {
public:

    // record the maximum depth
    int res = 0;
    // record the depth of the current node being traversed
    int depth = 0;

    // main function
    int maxDepth(TreeNode* root) {
        traverse(root);
        return res;
    }

    // binary tree traversal framework
    void traverse(TreeNode* root) {
        if (root == NULL) {
            // reached a leaf node
            res = max(res, depth);
            return;
        }
        // pre-order traversal position
        depth++;
        traverse(root->left);
        traverse(root->right);
        // post-order traversal position
        depth--;
    }
};

class Solution:
    def __init__(self):
        # record the maximum depth
        self.res = 0
        # record the depth of the current traversal node
        self.depth = 0
        
    def maxDepth(self, root: TreeNode) -> int:
        self.traverse(root)
        return self.res
        
    def traverse(self, root: TreeNode) -> None:
        if not root:
            # reached a leaf node
            self.res = max(self.res, self.depth)
            return
        # pre-order traversal position
        self.depth += 1
        self.traverse(root.left)
        self.traverse(root.right)
        # post-order traversal position
        self.depth -= 1

func maxDepth(root *TreeNode) int {
    // res records the maximum depth
    // depth records the depth of the current node being traversed
	res, depth := 0, 0
	traverse(root, &res, &depth)
	return res
}

func traverse(root *TreeNode, res *int, depth *int) {
	if root == nil {
		// reached a leaf node
		*res = max(*res, *depth)
		return
	}
	// pre-order traversal position
	*depth++
	traverse(root.left, res, depth)
	traverse(root.right, res, depth)
	// post-order traversal position
	*depth--
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

var maxDepth = function(root) {
    // record the maximum depth
    let res = 0;
    // record the depth of the current node being traversed
    let depth = 0;

    // main function
    function traverse(root) {
        if (root === null) {
            // reached a leaf node
            res = Math.max(res, depth);
            return;
        }
        // pre-order traversal position
        depth++;
        traverse(root.left);
        traverse(root.right);
        // post-order traversal position
        depth--;
    }

    traverse(root);
    return res;
};

This logic uses the traverse function to visit every node in the tree. It keeps track of the depth, and updates the maximum depth at leaf nodes.

Look at this code. Does it feel familiar? Can you relate it to the backtracking code template?

Try comparing it with the code for the permutation problem in Backtracking Framework. The backtrack function is just like the traverse function. The logic is almost the same:

class Solution {
    // record all permutations
    List<List<Integer>> res = new LinkedList<>();
    // record the current permutation being enumerated
    LinkedList<Integer> track = new LinkedList<>();

    // elements in track will be marked as true to avoid reuse
    boolean[] used;

    // main function, input a set of unique numbers, return all their permutations
    List<List<Integer>> permute(int[] nums) {
        used = new boolean[nums.length];
        
        backtrack(nums);
        return res;
    }

    // the core framework of the backtracking algorithm, traverse the
    // backtracking tree, collect all permutations at leaf nodes
    void backtrack(int[] nums) {
        // reached a leaf node, elements in track form a permutation
        if (track.size() == nums.length) {
            res.add(new LinkedList(track));
            return;
        }
        
        for (int i = 0; i < nums.length; i++) {
            // exclude invalid choices
            if (used[i]) {
                // nums[i] is already in track, skip
                continue;
            }
            // make a choice
            track.add(nums[i]);
            used[i] = true;

            // enter the next level of the recursion tree
            backtrack(nums);
            
            // undo the choice
            track.removeLast();
            used[i] = false;
        }
    }
}

class Solution {
public:
    // record all permutations
    vector<vector<int>> res;
    // record the current permutation being enumerated
    vector<int> track;

    // elements in track will be marked as true to avoid reuse
    vector<bool> used;

    // main function, input a set of unique numbers, return their permutations
    vector<vector<int>> permute(vector<int>& nums) {
        used = vector<bool>(nums.size(), false);
        
        backtrack(nums);
        return res;
    }

    // core framework of the backtracking algorithm, traverse the
    // backtracking tree, collect all permutations on the leaf nodes
    void backtrack(vector<int>& nums) {
        // reached a leaf node, elements in track form a permutation
        if (track.size() == nums.size()) {
            res.push_back(track);
            return;
        }
        
        for (int i = 0; i < nums.size(); i++) {
            // exclude illegal choices
            if (used[i]) {
                // nums[i] is already in track, skip
                continue;
            }
            // make a choice
            track.push_back(nums[i]);
            used[i] = true;

            // enter the next level of the recursive tree
            backtrack(nums);
            
            // undo the choice
            track.pop_back();
            used[i] = false;
        }
    }
};

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        # record all permutations
        res = []
        # record the current permutation being enumerated
        track = []

        # elements in track will be marked as true to avoid reuse
        used = [False] * len(nums)

        # main function, input a set of unique numbers, return all their permutations
        def backtrack(nums):
            # reach a leaf node, elements in track form a permutation
            if len(track) == len(nums):
                res.append(track[:])
                return

            for i in range(len(nums)):
                # exclude invalid choices
                if used[i]:
                    # nums[i] is already in track, skip
                    continue
                # make a choice
                track.append(nums[i])
                used[i] = True

                # enter the next level of the recursion tree
                backtrack(nums)

                # undo the choice
                track.pop()
                used[i] = False

        backtrack(nums)
        return res

func permute(nums []int) [][]int {
    // record all permutations
    var res [][]int
    // record the current permutation being enumerated
    var track []int

    // elements in track are marked as true to avoid reuse
    used := make([]bool, len(nums))

    // main function; input a set of distinct numbers and return their permutations
    backtrack(nums, &res, &track, used)
    return res
}

// core framework of backtracking algorithm, traverse the
// backtracking tree to collect all permutations at leaf nodes
func backtrack(nums []int, res *[][]int, track *[]int, used []bool) {
    // reach a leaf node, elements in track form a permutation
    if len(*track) == len(nums) {
        tmp := make([]int, len(*track))
        copy(tmp, *track)
        *res = append(*res, tmp)
        return
    }

    for i := 0; i < len(nums); i++ {
        // exclude invalid choices
        if used[i] {
            // nums[i] is already in track, skip it
            continue
        }
        // make a choice
        *track = append(*track, nums[i])
        used[i] = true

        // enter the next level of the recursion tree
        backtrack(nums, res, track, used)

        // undo the choice
        *track = (*track)[:len(*track)-1]
        used[i] = false
    }
}

var permute = function(nums) {
    // record all permutations
    let res = [];
    // record the current permutation being explored
    let track = [];

    // elements in track will be marked as true to avoid reuse
    let used = new Array(nums.length).fill(false);

    // main function, input a set of unique numbers, return their permutations
    function backtrack(nums) {
        // reached a leaf node, elements in track form a permutation
        if (track.length === nums.length) {
            res.push(track.slice());
            return;
        }

        for (let i = 0; i < nums.length; i++) {
            // exclude invalid choices
            if (used[i]) {
                // nums[i] is already in track, skip it
                continue;
            }
            // make a choice
            track.push(nums[i]);
            used[i] = true;

            // enter the next level of the recursive tree
            backtrack(nums);

            // undo the choice
            track.pop();
            used[i] = false;
        }
    }

    backtrack(nums);
    return res;
};

This code looks longer, but it's just a traversal of an N-ary tree. So, backtracking is really just tree traversal. If you can turn a problem into a tree, you can solve it with backtracking.

Decomposition Thinking Pattern

What does it mean to calculate the answer by breaking down the problem?

Still using the maximum depth problem, you can also solve it like this:

// definition: input the root node, return the maximum depth of this binary tree
int maxDepth(TreeNode root) {
	if (root == null) {
		return 0;
	}
	// recursively calculate the maximum depth of left and right subtrees
	int leftMax = maxDepth(root.left);
	int rightMax = maxDepth(root.right);
	// the maximum depth of the whole tree is the
// maximum depth of the left and right subtrees plus one
	int res = Math.max(leftMax, rightMax) + 1;

	return res;
}

// Definition: input the root node, return the maximum depth of the binary tree
int maxDepth(TreeNode* root) {
    if (root == nullptr) {
        return 0;
    }
    // Recursively calculate the maximum depth of the left and right subtrees
    int leftMax = maxDepth(root->left);
    int rightMax = maxDepth(root->right);
    // The maximum depth of the whole tree is the maximum
    // depth of the left and right subtrees plus one
    int res = max(leftMax, rightMax) + 1;

    return res;
}

# Definition: input the root node, return the maximum depth of this binary tree
def maxDepth(root: TreeNode) -> int:
    if root is None:
        return 0
    # Recursively calculate the maximum depth of the left and right subtrees
    leftMax = maxDepth(root.left)
    rightMax = maxDepth(root.right)
    # The maximum depth of the entire tree is the maximum
    # depth of the left and right subtrees plus one
    res = max(leftMax, rightMax) + 1

    return res

// Definition: input the root node, return the maximum depth of this binary tree
func maxDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    // recursively calculate the maximum depth of the left and right subtrees
    leftMax := maxDepth(root.left)
    rightMax := maxDepth(root.right)
    // the maximum depth of the entire tree is the maximum
    // depth of the left and right subtrees plus one
    res := max(leftMax, rightMax) + 1

    return res
}

// helper function
func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

// Definition: input the root node, return the maximum depth of this binary tree
var maxDepth = function(root) {
    if (root == null) {
        return 0;
    }
    // recursively calculate the maximum depth of the left and right subtrees
    let leftMax = maxDepth(root.left);
    let rightMax = maxDepth(root.right);
    // the maximum depth of the entire tree is the maximum
    // depth of the left and right subtrees plus one
    let res = Math.max(leftMax, rightMax) + 1;

    return res;
};

Does this code also look familiar? Does it look a bit like dynamic programming code?

Look at the brute-force solution for the coin change problem in Dynamic Programming Framework:

class Solution {
    public int coinChange(int[] coins, int amount) {
        // the final result required by the problem is dp(amount)
        return dp(coins, amount);
    }

    // definition: to make up the `amount`, at least dp(coins, amount) coins are needed
    int dp(int[] coins, int amount) {
        // base case
        if (amount == 0) return 0;
        if (amount < 0) return -1;

        int res = Integer.MAX_VALUE;
        for (int coin : coins) {
            // calculate the result of the subproblem
            int subProblem = dp(coins, amount - coin);
            // skip if the subproblem has no solution
            if (subProblem == -1) continue;
            // choose the optimal solution from the subproblem, then add one
            res = Math.min(res, subProblem + 1);
        }

        return res == Integer.MAX_VALUE ? -1 : res;
    }
}

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        // the final result required by the problem is dp(amount)
        return dp(coins, amount);
    }

private:
    // definition: to make up the `amount`, at least dp(coins, amount) coins are needed
    int dp(vector<int>& coins, int amount) {
        // base case
        if (amount == 0) return 0;
        if (amount < 0) return -1;

        int res = INT_MAX;
        for (int coin : coins) {
            // calculate the result of the subproblem
            int subProblem = dp(coins, amount - coin);
            // skip if the subproblem has no solution
            if (subProblem == -1) continue;
            // choose the optimal solution in the subproblem, then add one
            res = min(res, subProblem + 1);
        }

        return res == INT_MAX ? -1 : res;
    }
};

class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        # the final result required by the problem is dp(amount)
        return self.dp(coins, amount)

    # definition: to make up the `amount`, at least dp(coins, amount) coins are needed
    def dp(self, coins, amount):
        # base case
        if amount == 0: 
            return 0
        if amount < 0: 
            return -1

        res = float('inf')
        for coin in coins:
            # calculate the result of the subproblem
            subProblem = self.dp(coins, amount - coin)
            # skip if the subproblem has no solution
            if subProblem == -1: 
                continue
            # choose the optimal solution in the subproblem, then add one
            res = min(res, subProblem + 1)

        return res if res != float('inf') else -1

func coinChange(coins []int, amount int) int {
    // The final result required by the problem is dp(amount)
    return dp(coins, amount)
}

// Definition: to make up the `amount`, at least dp(coins, amount) coins are needed
func dp(coins []int, amount int) int {
    // base case
    if amount == 0 {
        return 0
    }
    if amount < 0 {
        return -1
    }

    res := math.MaxInt32
    for _, coin := range coins {
        // Calculate the result of the subproblem
        subProblem := dp(coins, amount - coin)
        // Skip if the subproblem has no solution
        if subProblem == -1 {
            continue
        }
        // Choose the optimal solution in the subproblem, then add one
        res = min(res, subProblem + 1)
    }

    if res == math.MaxInt32 {
        return -1
    }
    return res
}

func min(x, y int) int {
    if x < y {
        return x
    }
    return y
}

var coinChange = function(coins, amount) {
    // The final result required by the problem is dp(amount)
    return dp(coins, amount);
}

// Definition: to make up the `amount`, at least dp(coins, amount) coins are needed
function dp(coins, amount) {
    // base case
    if (amount === 0) return 0;
    if (amount < 0) return -1;

    let res = Number.MAX_SAFE_INTEGER;
    for (let coin of coins) {
        // Calculate the result of the subproblem
        let subProblem = dp(coins, amount - coin);
        // Skip if the subproblem has no solution
        if (subProblem === -1) continue;
        // Choose the optimal solution in the subproblem, then add one
        res = Math.min(res, subProblem + 1);
    }

    return res === Number.MAX_SAFE_INTEGER ? -1 : res;
}

Add a memo (memoization) to this brute-force solution, and you get top-down dynamic programming. Compare it with the code for the maximum depth of a binary tree. Do you see how similar they are?

Expanding Ideas

If you understand the difference between the two ways of solving the maximum depth problem, let’s keep going. Let me ask you: how do you write the preorder traversal of a binary tree?

I believe everyone can easily write the following code without hesitation:

List<Integer> res = new LinkedList<>();

// return the preorder traversal result
List<Integer> preorder(TreeNode root) {
    traverse(root);
    return res;
}

// binary tree traversal function
void traverse(TreeNode root) {
    if (root == null) {
        return;
    }
    // preorder traversal position
    res.add(root.val);
    traverse(root.left);
    traverse(root.right);
}

vector<int> res;

// return the preorder traversal results
vector<int> preorder(TreeNode* root) {
    traverse(root);
    return res;
}

// binary tree traversal function
void traverse(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    // preorder traversal position
    res.push_back(root->val);
    traverse(root->left);
    traverse(root->right);
}

class Solution:
    def __init__(self):
        # create a list as the result container
        self.res = []

    # return the preorder traversal result
    def preorder(self, root: TreeNode) -> List[int]:
        self.traverse(root)
        return self.res

    # binary tree traversal function
    def traverse(self, root: TreeNode) -> None:
        if not root:
            return
        # position for preorder traversal
        self.res.append(root.val)
        self.traverse(root.left)
        self.traverse(root.right)

// return the preorder traversal result
func preorder(root *TreeNode) []int {
    var res []int
    traverse(root, &res)
    return res
}

// binary tree traversal function
func traverse(root *TreeNode, res *[]int) {
    if root == nil {
        return
    }
    // preorder traversal position
    *res = append(*res, root.Val)
    traverse(root.Left, res)
    traverse(root.Right, res)
}

// return the preorder traversal result
function preorder(root) {
    let res = [];

    // binary tree traversal function
    function traverse(root) {
        if (root === null) {
            return;
        }
        // preorder traversal position
        res.push(root.val);
        traverse(root.left);
        traverse(root.right);
    }

    traverse(root);
    return res;
}

But if you think about the two problem-solving approaches above, can binary tree traversal also be solved by breaking down the problem?

Let’s look at the result of preorder traversal:

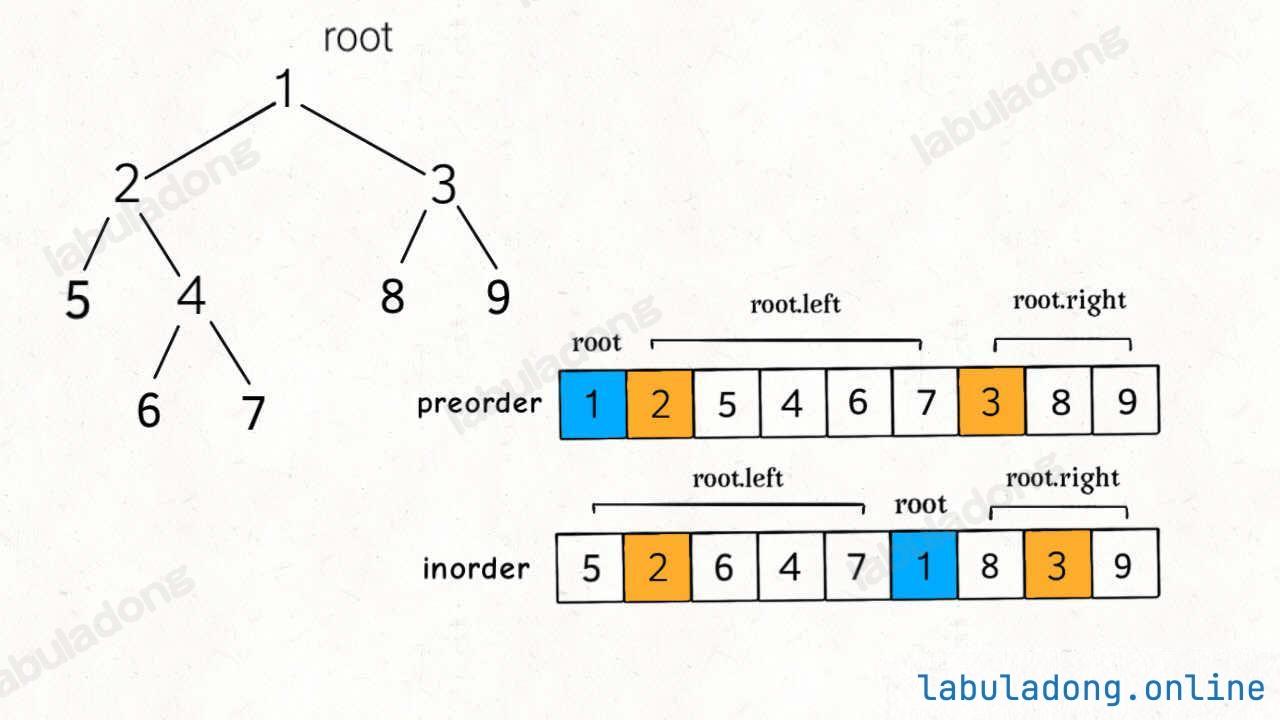
Notice that in preorder traversal, the root node comes first, then the preorder result of the left subtree, and finally the preorder result of the right subtree.

Do you see something here? You can actually rewrite the preorder traversal code using the idea of breaking down the problem:

// Definition: input the root node of a binary tree,
// return the preorder traversal result of this tree
List<Integer> preorder(TreeNode root) {
    List<Integer> res = new LinkedList<>();
    if (root == null) {
        return res;
    }
    // The result of preorder traversal, root.val is first
    res.add(root.val);
    // Followed by the preorder traversal result of the left subtree
    res.addAll(preorder(root.left));
    // Finally followed by the preorder traversal result of the right subtree
    res.addAll(preorder(root.right));
    return res;
}

// Definition: input the root of a binary tree,
// return the preorder traversal result of this tree
vector<int> preorder(TreeNode* root) {
    vector<int> res;
    if (root == nullptr) {
        return res;
    }
    // The preorder traversal result, root->val is first
    res.push_back(root->val);
    // Followed by the preorder traversal result of the left subtree
    vector<int> left = preorder(root->left);
    res.insert(res.end(), left.begin(), left.end());
    // Finally, followed by the preorder traversal result of the right subtree
    vector<int> right = preorder(root->right);
    res.insert(res.end(), right.begin(), right.end());
    return res;
}

from typing import List

# Definition: Given the root node of a binary tree,
# return the preorder traversal result of this tree
def preorder(root: TreeNode) -> List[int]:
    res = []
    if not root:
        return res
    # In the result of preorder traversal, root.val is the first
    res.append(root.val)
    # Then append the preorder traversal result of the left subtree
    res.extend(preorder(root.left))
    # Finally, append the preorder traversal result of the right subtree
    res.extend(preorder(root.right))
    return res

// Definition: Input the root node of a binary tree,
// return the preorder traversal result of this tree
func preorder(root *TreeNode) []int {
    res := []int{}
    if root == nil {
        return res
    }
    // The result of preorder traversal, root.val is the first
    res = append(res, root.val)
    // Followed by the preorder traversal result of the left subtree
    res = append(res, preorder(root.left)...)
    // Finally followed by the preorder traversal result of the right subtree
    res = append(res, preorder(root.right)...)
    return res
}

// Definition: given the root of a binary tree,
// return the preorder traversal result of this tree
var preorder = function(root) {
    var res = [];
    if (root === null) {
        return res;
    }
    // In the preorder traversal result, root.val is the first
    res.push(root.val);
    // Followed by the preorder traversal result of the left subtree
    res = res.concat(preorder(root.left));
    // Finally followed by the preorder traversal result of the right subtree
    res = res.concat(preorder(root.right));
    return res;
};

This is the preorder traversal written with the "decompose the problem" mindset. Inorder and postorder traversals can be written in a similar way.

Level Order Traversal

Besides dynamic programming, backtracking (DFS), and divide and conquer, another common algorithm is BFS. The BFS algorithm framework is based on the following level order traversal code for binary trees:

// Input the root node of a binary tree, perform level-order traversal on the binary tree
void levelTraverse(TreeNode root) {
    if (root == null) return;
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);

    int depth = 1;
    // Traverse each level of the binary tree from top to bottom
    while (!q.isEmpty()) {
        int sz = q.size();
        // Traverse each node of the level from left to right
        for (int i = 0; i < sz; i++) {
            TreeNode cur = q.poll();

            // put the nodes of the next level into the queue
            if (cur.left != null) {
                q.offer(cur.left);
            }
            if (cur.right != null) {
                q.offer(cur.right);
            }
        }
        depth++;
    }
}

// input the root node of a binary tree, perform a level order traversal of the tree
int levelTraverse(TreeNode* root) {
    if (root == nullptr) return;
    queue<TreeNode*> q;
    q.push(root);

    int depth = 0;
    // traverse each level of the binary tree from top to bottom
    while (!q.empty()) {
        int sz = q.size();
        // traverse each node of the level from left to right
        for (int i = 0; i < sz; i++) {
            TreeNode* cur = q.front();
            q.pop();

            // put the nodes of the next level into the queue
            if (cur->left != nullptr) {
                q.push(cur->left);
            }
            if (cur->right != nullptr) {
                q.push(cur->right);
            }
        }
        depth++;
    }
    return depth;
}

# input the root of a binary tree, perform level order traversal of this binary tree
class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root:
            return
        q = collections.deque()
        q.append(root)
        depth = 0
        # traverse each level of the binary tree from top to bottom
        while q:
            sz = len(q)
            # traverse each node of each level from left to right
            for i in range(sz):
                cur = q.popleft()

                # put the nodes of the next level into the queue
                if cur.left:
                    q.append(cur.left)
                if cur.right:
                    q.append(cur.right)
            depth += 1

// Input the root node of a binary tree and perform level order traversal of this binary tree
func levelTraverse(root *TreeNode) {
    if root == nil {
        return
    }

    q := make([]*TreeNode, 0)
    q = append(q, root)
    depth := 1

    // Traverse each level of the binary tree from top to bottom
    for len(q) > 0 {
        sz := len(q)

        // Traverse each node of each level from left to right
        for i := 0; i < sz; i++ {
            cur := q[0]
            q = q[1:]

            // put the nodes of the next level into the queue
            if cur.Left != nil {
                q = append(q, cur.Left)
            }
            if cur.Right != nil {
                q = append(q, cur.Right) 
            }
        }
        depth++
    }
}

// input the root node of a binary tree, perform level-order traversal of this binary tree
var levelTraverse = function(root) {
    if (root == null) return;
    var q = [];
    q.push(root);

    var depth = 1;
    // traverse each level of the binary tree from top to bottom
    while (q.length > 0) {
        var sz = q.length;
        // traverse each node of each level from left to right
        for (var i = 0; i < sz; i++) {
            var cur = q.shift();

            // put the nodes of the next level into the queue
            if (cur.left != null) {
                q.push(cur.left);
            }
            if (cur.right != null) {
                q.push(cur.right);
            }
        }
        depth++;
    }
}

Going further, graph algorithms are also extensions of binary tree algorithms.

For example, Basic Graph Theory, Cycle Detection and Topological Sort, and Bipartite Graph Algorithm use DFS. Also, Dijkstra Algorithm Template is an improved version of BFS.

To sum up, these algorithms are basically brute-forcing binary (or multiway) trees. If you can prune branches or use memoization, you can reduce extra work and improve efficiency. That’s the main idea.

Final Summary

Many people ask me what is the right way to practice coding problems. I think the right way is to solve one problem and learn enough so you get the value of solving ten. Otherwise, if there are 2,000 problems on LeetCode, are you planning to finish all of them?

How to do this? You need a framework mindset, learn to find the key points, and look for what doesn’t change. A single algorithm trick can show up in thousands of problems. If you can see through them, then a thousand problems are just one. Why waste time?

This is the power of frameworks. It helps you write correct code even when you're tired. Even if you haven't learned much, this way of thinking puts you at a higher level.

Teaching someone how to fish is better than giving them a fish. Algorithms aren’t really hard. If you want to learn, anyone can do it. I hope you can develop a systematic way of thinking here, enjoy mastering algorithms, and not be controlled by them.