Classic DP: Minimum Path Sum

Today, let's discuss a classic dynamic programming problem, which is LeetCode Problem 64: Minimum Path Sum:

64. Minimum Path Sum | LeetCode |  🟠

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right, which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

Example 1:

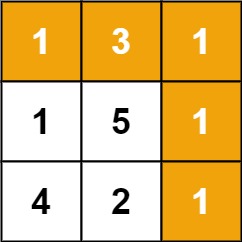
Input: grid = [[1,3,1],[1,5,1],[4,2,1]]
Output: 7
Explanation: Because the path 1 → 3 → 1 → 1 → 1 minimizes the sum.

Example 2:

Input: grid = [[1,2,3],[4,5,6]]
Output: 12

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• 0 <= grid[i][j] <= 200

The problem is from LeetCode 64. Minimum Path Sum.

The function signature is as follows:

int minPathSum(int[][] grid);

int minPathSum(vector<vector<int>>& grid);

def minPathSum(grid: List[List[int]]) -> int

func minPathSum(grid [][]int) int {}

var minPathSum = function(grid) {}

In fact, this problem is not very difficult, but you might encounter some more challenging variations. Therefore, it's essential to discuss a general approach for such problems.

Generally, when asked to solve optimization problems (finding maximum or minimum values) in a 2D matrix, recursion combined with memoization, also known as dynamic programming techniques, is necessary.

Take the example given in the problem; I've numbered some of the grid squares in the image for easier explanation:

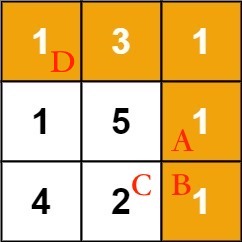
We want to calculate the minimum path sum from the starting point D to B. How can you reach B?

The problem states you can only move right or down, so you can only reach B from A or C.

How does the algorithm determine that moving from A to B results in the minimum path sum, rather than from C to B?

Is it because the element at position A is 1 and the element at position C is 2, and 1 is less than 2, so you must move from A to B to achieve the minimum path sum?

Actually, it's not. The real reason is that the minimum path sum from D to A is 6, while from D to C, it is 8. Since 6 is less than 8, you must move from A to B to achieve the minimum path sum.

In other words, we transformed the problem of "finding the minimum path sum from D to B" into the problems of "finding the minimum path sum from D to A" and "finding the minimum path sum from D to C."

Understanding the above analysis reveals a state transition equation, indicating that this problem will certainly use dynamic programming techniques to be solved.

For example, we can define a dp function as follows:

int dp(int[][] grid, int i, int j);

int dp(int grid[][], int i, int j);

def dp(grid: List[List[int]], i: int, j: int) -> int:

func dp(grid [][]int, i int, j int) int {}

var dp = function(grid, i, j) {}

The definition of this dp function is as follows:

The minimum path sum from the top-left corner position (0, 0) to the position (i, j) is dp(grid, i, j).

Based on this definition, the minimum path sum we want to find can be calculated by calling this dp function:

int minPathSum(int[][] grid) {
    int m = grid.length;
    int n = grid[0].length;
    // calculate the minimum path sum from the top-left corner to the bottom-right corner
    return dp(grid, m - 1, n - 1);
}

int minPathSum(vector<vector<int>>& grid) {
    int m = grid.size();
    int n = grid[0].size();
    // calculate the minimum path sum from the top-left corner to the bottom-right corner
    return dp(grid, m - 1, n - 1);
}

def minPathSum(grid: List[List[int]]) -> int:
    m = len(grid)
    n = len(grid[0])
    # calculate the minimum path sum from the top-left corner to the bottom-right corner
    return dp(grid, m - 1, n - 1)

func minPathSum(grid [][]int) int {
    m := len(grid)
    n := len(grid[0])
    // calculate the minimum path sum from the top-left corner to the bottom-right corner
    return dp(grid, m-1, n-1)
}

var minPathSum = function(grid) {
    var m = grid.length;
    var n = grid[0].length;
    // calculate the minimum path sum from the top-left corner to the bottom-right corner
    return dp(grid, m - 1, n - 1);
};

Based on the previous analysis, it's easy to see that the value of dp(grid, i, j) depends on the values returned by dp(grid, i - 1, j) and dp(grid, i, j - 1).

We can now write the code directly:

int dp(int[][] grid, int i, int j) {
    // base case
    if (i == 0 && j == 0) {
        return grid[0][0];
    }
    // if the index is out of bounds, return a very large value,
    // ensuring it won't be selected when taking the min
    if (i < 0 || j < 0) {
        return Integer.MAX_VALUE;
    }

    // the minimum path sum of the left and above plus grid[i][j]
    // is the minimum path sum to reach (i, j)
    return Math.min(
            dp(grid, i - 1, j), 
            dp(grid, i, j - 1)
        ) + grid[i][j];
}

int dp(vector<vector<int>>& grid, int i, int j) {
    // base case
    if (i == 0 && j == 0) {
        return grid[0][0];
    }
    // if the index is out of bounds, return a very large value,
    // ensuring it won't be chosen when taking the min
    if (i < 0 || j < 0) {
        return INT_MAX;
    }

    // the minimum path sum of the left and above plus grid[i][j]
    // is the minimum path sum to reach (i, j)
    return min(
            dp(grid, i - 1, j), 
            dp(grid, i, j - 1)
        ) + grid[i][j];
}

def dp(grid: List[List[int]], i: int, j: int) -> int:
    # base case
    if i == 0 and j == 0:
        return grid[0][0]

    # if the index is out of bounds, return a very large value,
    # ensuring it won't be chosen when taking the minimum
    if i < 0 or j < 0:
        return float('inf')

    # the minimum path sum from the left and above plus grid[i][j]
    # is the minimum path sum to reach (i, j)
    return min(
            dp(grid, i - 1, j), 
            dp(grid, i, j - 1)
        ) + grid[i][j]

func dp(grid [][]int, i int, j int) int {
    // base case
    if i == 0 && j == 0 {
        return grid[0][0]
    }
    // if the index is out of bounds, return a very large value,
    // to ensure it is not selected when taking the min
    if i < 0 || j < 0 {
        return math.MaxInt32
    }

    // the minimum path sum of the left and above plus grid[i][j]
    // is the minimum path sum to reach (i, j)
    return min(
            dp(grid, i - 1, j), 
            dp(grid, i, j - 1)
        ) + grid[i][j]
}

func min(a int, b int) int {
    if a < b {
        return a
    }
    return b
}

var dp = function(grid, i, j) {
  // base case
  if (i == 0 && j == 0) {
    return grid[0][0];
  }
  // if the index is out of bounds, return a very large value,
  // to ensure it is not chosen when taking the minimum
  if (i < 0 || j < 0) {
    return Number.MAX_VALUE;
  }
  
  // the minimum path sum from the left and above plus grid[i][j]
  // is the minimum path sum to reach (i, j)
  return Math.min(
    dp(grid, i - 1, j), 
    dp(grid, i, j - 1)
  ) + grid[i][j];
}

The logic of the above code is complete. Next, let's analyze whether this recursive algorithm has overlapping subproblems and if we need to use memoization to optimize its efficiency.

As mentioned multiple times in previous sections, the technique to identify overlapping subproblems is to abstract the recursive framework of the above code:

int dp(int i, int j) {
    dp(i - 1, j); // #1
    dp(i, j - 1); // #2
}

If I want to recurse from dp(i, j) to dp(i-1, j-1), how many different recursive call paths are there?

It can be dp(i, j) -> #1 -> #2 or dp(i, j) -> #2 -> #1. Since there is more than one path, it means dp(i-1, j-1) will be calculated multiple times, indicating that there are overlapping subproblems.

Therefore, we can use memoization to optimize it:

class Solution {
    // memoization table
    int[][] memo;

    public int minPathSum(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        // construct the memoization table with initial values set to -1
        memo = new int[m][n];
        for (int[] row : memo)
            Arrays.fill(row, -1);
        
        return dp(grid, m - 1, n - 1);
    }

    int dp(int[][] grid, int i, int j) {
        // base case
        if (i == 0 && j == 0) {
            return grid[0][0];
        }
        if (i < 0 || j < 0) {
            return Integer.MAX_VALUE;
        }
        // avoid repeated calculations
        if (memo[i][j] != -1) {
            return memo[i][j];
        }
        // record the calculation result in the memoization table
        memo[i][j] = Math.min(
            dp(grid, i - 1, j),
            dp(grid, i, j - 1)
        ) + grid[i][j];

        return memo[i][j];
    }
}

class Solution {
private:
    // memoization
    vector<vector<int>> memo;

    int dp(vector<vector<int>> &grid, int i, int j) {
        // base case
        if (i == 0 && j == 0) {
            return grid[0][0];
        }
        if (i < 0 || j < 0) {
            return INT_MAX;
        }
        // avoid repeated calculations
        if (memo[i][j] != -1) {
            return memo[i][j];
        }
        // record the calculation result in the memo
        memo[i][j] = min(
            dp(grid, i - 1, j),
            dp(grid, i, j - 1)
        ) + grid[i][j];

        return memo[i][j];
    }

public:
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        // construct the memo, initialize all values to -1
        memo = vector<vector<int>>(m, vector<int>(n, -1));
        return dp(grid, m - 1, n - 1);
    }
};

class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        # construct a memoization table with all initial values set to -1
        memo = [[-1 for _ in range(n)] for _ in range(m)]

        def dp(i, j):
            # base case
            if i == 0 and j == 0:
                return grid[0][0]
            if i < 0 or j < 0:
                return float('inf')
            # avoid redundant calculations
            if memo[i][j] != -1:
                return memo[i][j]
            # record the calculation result in the memoization table
            memo[i][j] = min(
                dp(i - 1, j),
                dp(i, j - 1)
            ) + grid[i][j]

            return memo[i][j]
        
        return dp(m - 1, n - 1)

func minPathSum(grid [][]int) int {
    // construct the memoization table
    memo := make([][]int, len(grid))
    for i := range memo {
        memo[i] = make([]int, len(grid[0]))
        for j := range memo[i] {
            memo[i][j] = -1
        }
    }

    return dp(grid, len(grid)-1, len(grid[0])-1, memo)
}

func dp(grid [][]int, i int, j int, memo [][]int) int {
    // base case
    if i == 0 && j == 0 {
        return grid[0][0]
    }
    if i < 0 || j < 0 {
        return math.MaxInt32
    }
    // avoid repeated calculations
    if memo[i][j] != -1 {
        return memo[i][j]
    }
    // record the calculation result in the memoization table
    memo[i][j] = int(math.Min(
        float64(dp(grid, i-1, j, memo)),
        float64(dp(grid, i, j-1, memo)),
    )) + grid[i][j]

    return memo[i][j]
}

var minPathSum = function(grid) {
    var m = grid.length;
    var n = grid[0].length;
    // construct a memoization table, initialize all values to -1
    var memo = new Array(m).fill(0).map(() => new Array(n).fill(-1));

    function dp(i, j) {
        // base case
        if (i == 0 && j == 0) {
            return grid[0][0];
        }
        if (i < 0 || j < 0) {
            return Number.MAX_VALUE;
        }
        // avoid repeated calculations
        if (memo[i][j] != -1) {
            return memo[i][j];
        }
        // record the calculation result in the memoization table
        memo[i][j] = Math.min(
            dp(i - 1, j),
            dp(i, j - 1)
        ) + grid[i][j];

        return memo[i][j];
    }

    return dp(m - 1, n - 1);
};

At this point, the problem is considered solved, with both time and space complexity being $O(MN)$, which is a standard top-down dynamic programming solution.

Some readers might ask if it's possible to solve this problem using a bottom-up iterative approach? It is absolutely possible.

First, similar to the previous dp function, we need a two-dimensional dp array, defined as follows:

The minimum path sum to reach position (i, j) from the top-left position (0, 0) is dp[i][j].

The state transition equation remains unchanged, as dp[i][j] still depends on dp[i-1][j] and dp[i][j-1]. Let's look directly at the code:

class Solution {
    public int minPathSum(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int[][] dp = new int[m][n];

        // **** base case ****
        dp[0][0] = grid[0][0];

        for (int i = 1; i < m; i++)
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        
        for (int j = 1; j < n; j++)
            dp[0][j] = dp[0][j - 1] + grid[0][j];        
        // *******************
        
        // state transition
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = Math.min(
                    dp[i - 1][j],
                    dp[i][j - 1]
                ) + grid[i][j];
            }
        }

        return dp[m - 1][n - 1];
    }
}

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        vector<vector<int>> dp(m, vector<int>(n, 0));

        // **** base case ****
        dp[0][0] = grid[0][0];

        for (int i = 1; i < m; i++)
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        
        for (int j = 1; j < n; j++)
            dp[0][j] = dp[0][j - 1] + grid[0][j];
        // *******************

        // state transition
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = min(
                    dp[i - 1][j],
                    dp[i][j - 1]
                ) + grid[i][j];
            }
        }

        return dp[m - 1][n - 1];
    }
};

class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        m = len(grid)
        n = len(grid[0])
        dp = [[0] * n for _ in range(m)]

        # **** base case ****
        dp[0][0] = grid[0][0]

        for i in range(1, m):
            dp[i][0] = dp[i - 1][0] + grid[i][0]
        
        for j in range(1, n):
            dp[0][j] = dp[0][j - 1] + grid[0][j]        
        # *******************
        
        # state transition
        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = min(
                    dp[i - 1][j],
                    dp[i][j - 1]
                ) + grid[i][j]

        return dp[m - 1][n - 1]

func minPathSum(grid [][]int) int {
	m := len(grid)
	n := len(grid[0])
	dp := make([][]int, m)
	for i := range dp {
		dp[i] = make([]int, n)
	}

	// **** base case ****
	dp[0][0] = grid[0][0]

	for i := 1; i < m; i++ {
		dp[i][0] = dp[i-1][0] + grid[i][0]
	}

	for j := 1; j < n; j++ {
		dp[0][j] = dp[0][j-1] + grid[0][j]
	}
	// *******************

	// state transition
	for i := 1; i < m; i++ {
		for j := 1; j < n; j++ {
			dp[i][j] = min(
				dp[i-1][j],
				dp[i][j-1],
			) + grid[i][j]
		}
	}

	return dp[m-1][n-1]
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

var minPathSum = function(grid) {
    var m = grid.length;
    var n = grid[0].length;
    var dp = new Array(m).fill(0).map(() => new Array(n).fill(0));

    // **** base case ****
    dp[0][0] = grid[0][0];

    for (let i = 1; i < m; i++)
        dp[i][0] = dp[i - 1][0] + grid[i][0];
    
    for (let j = 1; j < n; j++)
        dp[0][j] = dp[0][j - 1] + grid[0][j];        
    // *******************
    
    // state transition
    for (let i = 1; i < m; i++) {
        for (let j = 1; j < n; j++) {
            dp[i][j] = Math.min(
                dp[i - 1][j],
                dp[i][j - 1]
            ) + grid[i][j];
        }
    }

    return dp[m - 1][n - 1];
};

The base case for this solution seems slightly different from the recursive solution, but they are actually the same.

This is because the state transition is represented by the following code:

dp[i][j] = Math.min(
    dp[i - 1][j],
    dp[i][j - 1]
) + grid[i][j];

If i or j equals 0, an index out of bounds error will occur.

Therefore, we need to pre-calculate dp[0][..] and dp[..][0], and then start iterating with i and j from 1.

How do we calculate the values of dp[0][..] and dp[..][0]? It's actually quite simple, as the path sums for the first row and first column only have the following scenario:

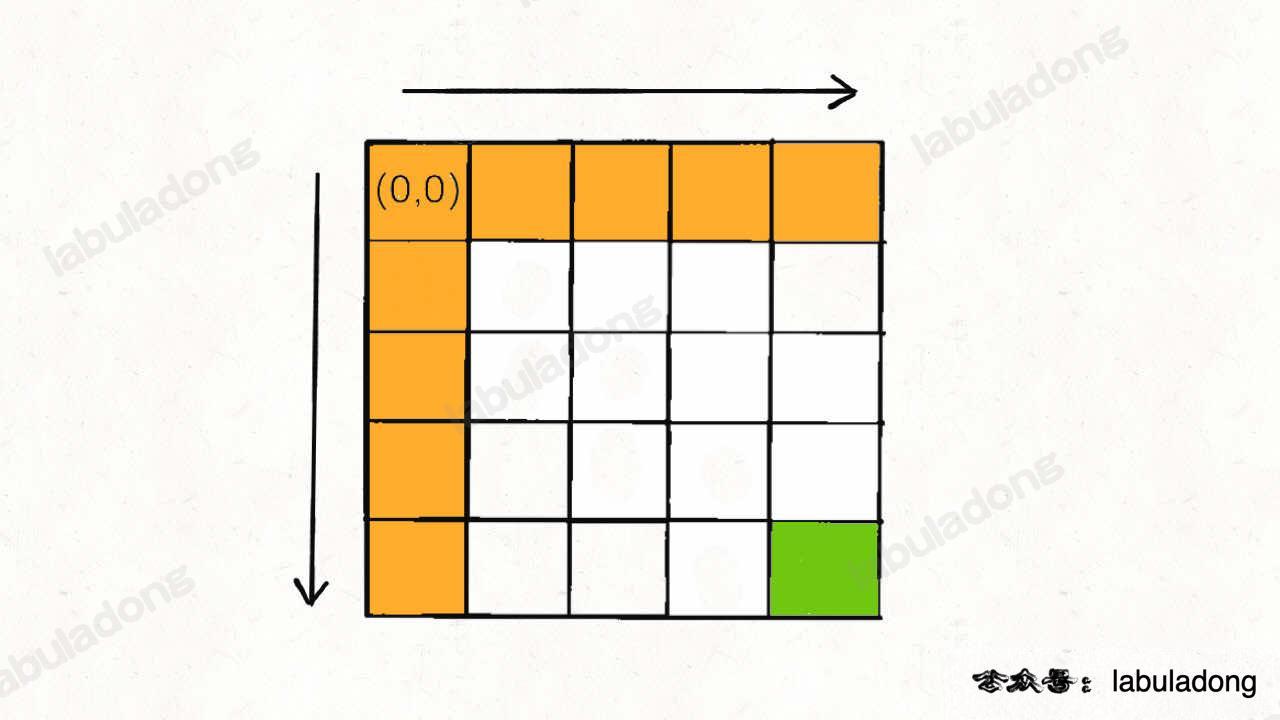
According to the definition of the dp array, dp[i][0] = sum(grid[0..i][0]) and dp[0][j] = sum(grid[0][0..j]), which can be implemented with the following code:

// **** base case ****
dp[0][0] = grid[0][0];

for (int i = 1; i < m; i++)
    dp[i][0] = dp[i - 1][0] + grid[i][0];

for (int j = 1; j < n; j++)
    dp[0][j] = dp[0][j - 1] + grid[0][j];        
// *******************

At this point, we've also covered the bottom-up iterative solution. Some readers might be wondering, can we optimize the space complexity of the algorithm?

In a previous article Dimensionality Reduction in Dynamic Programming: Space Compression, we discussed techniques for reducing the size of the dp array, which are applicable here as well, though slightly more complex. Due to space limitations in this article, we won't cover it here. Interested readers are encouraged to try it out on their own.

This concludes our article. In the next one, we'll tackle an advanced problem that is even more ingenious and interesting. Stay tuned!