How to Determine the Base Case and Initial Values for Memoization?
This article will resolve
| LeetCode | Difficulty |
|---|---|
| 931. Minimum Falling Path Sum | 🟠 |
Many readers have questions about the base case, and initial values in the memoization table for dynamic programming problems. In this article, I will explain these topics. I will also talk about how to find hints in the problem to help us solve it.
Let's look at LeetCode problem 931: Minimum Falling Path Sum. The input is an n * n 2D array matrix. You need to calculate the minimum path sum from the first row to the last row.
931. Minimum Falling Path Sum | LeetCode | 🟠
Given an n x n array of integers matrix, return the minimum sum of any falling path through matrix.
A falling path starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position (row, col) will be (row + 1, col - 1), (row + 1, col), or (row + 1, col + 1).
Example 1:
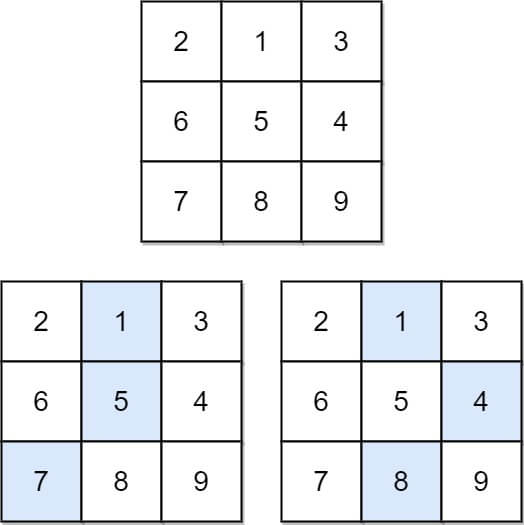
Input: matrix = [[2,1,3],[6,5,4],[7,8,9]] Output: 13 Explanation: There are two falling paths with a minimum sum as shown.
Example 2:
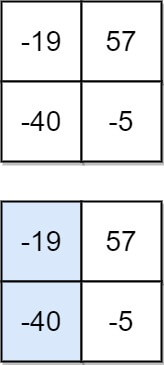
Input: matrix = [[-19,57],[-40,-5]] Output: -59 Explanation: The falling path with a minimum sum is shown.
Constraints:
n == matrix.length == matrix[i].length1 <= n <= 100-100 <= matrix[i][j] <= 100
The function signature is:
int minFallingPathSum(int[][] matrix);int minFallingPathSum(vector<vector<int>>& matrix);def minFallingPathSum(matrix: List[List[int]]) -> intfunc minFallingPathSum(matrix [][]int) int {}var minFallingPathSum = function(matrix) {}This problem is not very difficult. I will use it as an example to explain how to decide the return value of the base case, the initial value in the memoization table, and what to return when the index goes out of bounds.
But first, let's use the standard dynamic programming approach to explain how to solve this problem.