Play Dungeon Game with DP

"The Magic Tower" is a classic dungeon crawler game where you lose health when encountering monsters, gain health by consuming health potions, collect keys, and advance through levels to ultimately rescue the beautiful princess.

This game is still available on mobile devices today:

Many people probably have fond childhood memories of this game. I remember playing it alone on a gaming device, surrounded by two or three friends giving directions, which made the gaming experience quite frustrating for the player but extremely enjoyable for the onlookers 😂.

LeetCode Problem 174, "Dungeon Game" is a similar challenge:

174. Dungeon Game | LeetCode |  🔴

The demons had captured the princess and imprisoned her in the bottom-right corner of a dungeon. The dungeon consists of m x n rooms laid out in a 2D grid. Our valiant knight was initially positioned in the top-left room and must fight his way through dungeon to rescue the princess.

The knight has an initial health point represented by a positive integer. If at any point his health point drops to 0 or below, he dies immediately.

Some of the rooms are guarded by demons (represented by negative integers), so the knight loses health upon entering these rooms; other rooms are either empty (represented as 0) or contain magic orbs that increase the knight's health (represented by positive integers).

To reach the princess as quickly as possible, the knight decides to move only rightward or downward in each step.

Return the knight's minimum initial health so that he can rescue the princess.

Note that any room can contain threats or power-ups, even the first room the knight enters and the bottom-right room where the princess is imprisoned.

Example 1:

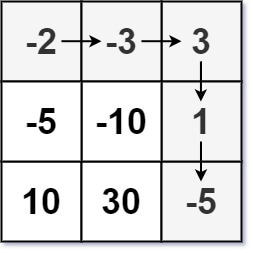
Input: dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]]
Output: 7
Explanation: The initial health of the knight must be at least 7 if he follows the optimal path: RIGHT-> RIGHT -> DOWN -> DOWN.

Example 2:

Input: dungeon = [[0]]
Output: 1

Constraints:

• m == dungeon.length
• n == dungeon[i].length
• 1 <= m, n <= 200
• -1000 <= dungeon[i][j] <= 1000

The problem is from LeetCode 174. Dungeon Game.

In simple terms, it asks how much initial health is needed for a knight to move from the top-left corner to the bottom-right corner, ensuring the health is always greater than 0.

The function signature is as follows:

int calculateMinimumHP(int[][] grid);

int calculateMinimumHP(vector<vector<int>>& grid);

def calculateMinimumHP(grid: List[List[int]]) -> int:

func calculateMinimumHP(grid [][]int) int

var calculateMinimumHP = function(grid) {}

The previous article Minimum Path Sum discussed a similar problem, asking for the minimum path sum from the top-left corner to the bottom-right corner.

When solving algorithm problems, we should always try to draw inferences from one instance to another. It feels like today's problem is somewhat related to the minimum path sum, right?

Minimizing the knight's initial health means maximizing the health potions along the knight's path. Isn't it equivalent to finding the "maximum path sum"? Can we directly apply the thought process of calculating the "minimum path sum"?

However, after some thought, this inference does not hold; collecting the most health potions does not necessarily result in the minimum initial health.

For example, in the following case, if you want to collect the most potions for the "maximum path sum," you should follow the path shown by the arrows in the image below, requiring an initial health of 11:

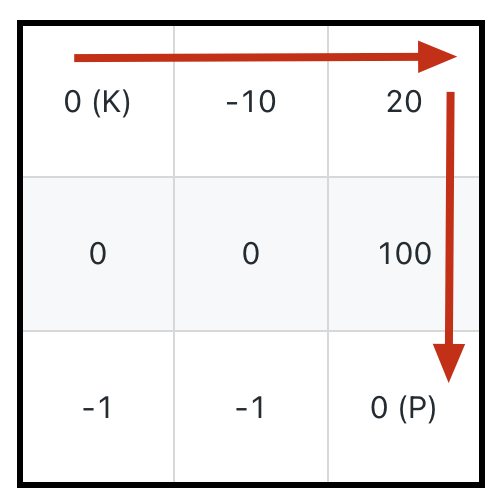
But it's easy to see that the correct path is shown by the arrows in the image below, requiring only an initial health of 1:

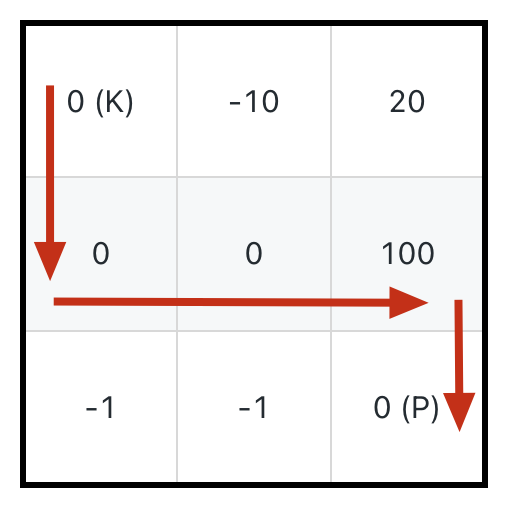
So, the key is not in collecting the most potions but in losing the least health.

For such optimization problems, dynamic programming techniques must be used, and the dp array/function definition must be designed appropriately. Referring to the previous article Minimum Path Sum Problem, the dp function signature will likely be as follows:

int dp(int[][] grid, int i, int j);

int dp(vector<vector<int>>& grid, int i, int j);

def dp(grid: List[List[int]], i: int, j: int) -> int:

func dp(grid [][]int, i int, j int) int {}

var dp = function(grid, i, j) {}

However, the definition of the dp function in this problem is quite interesting. Logically, the dp function should be defined as:

The minimum health required to reach grid[i][j] from the top-left corner (grid[0][0]) is dp(grid, i, j).

With this definition, the base case occurs when both i and j equal 0, and we can write the code as follows:

int calculateMinimumHP(int[][] grid) {
    int m = grid.length;
    int n = grid[0].length;
    // We want to calculate the minimum health required from
    // the top-left corner to the bottom-right corner
    return dp(grid, m - 1, n - 1);
}

int dp(int[][] grid, int i, int j) {
    // base case
    if (i == 0 && j == 0) {
        // Ensure the knight survives the landing
        return grid[i][j] > 0 ? 1 : -grid[i][j] + 1;
    }
    ...
}

int dp(vector<vector<int>>& grid, int i, int j) {
    // base case
    if (i == 0 && j == 0) {
        // ensure the knight survives upon landing
        return grid[i][j] > 0 ? 1 : -grid[i][j] + 1;
    }
    ...
}

int calculateMinimumHP(vector<vector<int>>& grid) {
    int m = grid.size();
    int n = grid[0].size();
    // we want to calculate the minimum health required from
    // the top-left corner to the bottom-right corner
    return dp(grid, m - 1, n - 1);
}

def calculateMinimumHP(grid: List[List[int]]) -> int:
    m = len(grid)
    n = len(grid[0])
    # we want to calculate the minimum health required
    # from the top-left corner to the bottom-right corner
    return dp(grid, m - 1, n - 1)

def dp(grid: List[List[int]], i: int, j: int) -> int:
    # base case
    if i == 0 and j == 0:
        # ensure the knight survives upon landing
        return 1 if grid[i][j] > 0 else -grid[i][j] + 1
    ...

func calculateMinimumHP(grid [][]int) int {
    m := len(grid)
    n := len(grid[0])
    // we want to calculate the minimum health value needed
    // from the top-left corner to the bottom-right corner
    return dp(grid, m-1, n-1)
}

func dp(grid [][]int, i int, j int) int {
    // base case
    if i == 0 && j == 0 {
        // ensure the knight survives the landing
        if grid[i][j] > 0 {
            return 1
        } else {
            return -grid[i][j] + 1
        }
    }
    ...
}

var calculateMinimumHP = function(grid) {
    var m = grid.length;
    var n = grid[0].length;
    // We want to calculate the minimum health required from
    // the top-left corner to the bottom-right corner
    return dp(grid, m - 1, n - 1);
}

var dp = function(grid, i, j) {
    // base case
    if (i == 0 && j == 0) {
        // Ensure the knight survives the landing
        return grid[i][j] > 0 ? 1 : -grid[i][j] + 1;
    }
    ...
}

For simplicity, we will abbreviate dp(grid, i, j) as dp(i, j) from now on, and you should understand the context.

Next, we need to find the state transition. Do you remember how to derive the state transition equation? Can we correctly perform state transitions with this definition of the dp function?

We want dp(i, j) to be derived from dp(i-1, j) and dp(i, j-1), so that we can progressively approach the base case and ensure correct state transitions.

Specifically, the "minimum health required to reach A" should be deduced from the "minimum health required to reach B" and the "minimum health required to reach C":

But the problem is, can we derive it? In fact, we cannot.

According to the definition of the dp function, you only know the "minimum health required to reach B from the top left corner," but you do not know the "health level when reaching B."

The "health level when reaching B" is a necessary reference for state transitions. Let me give you an example:

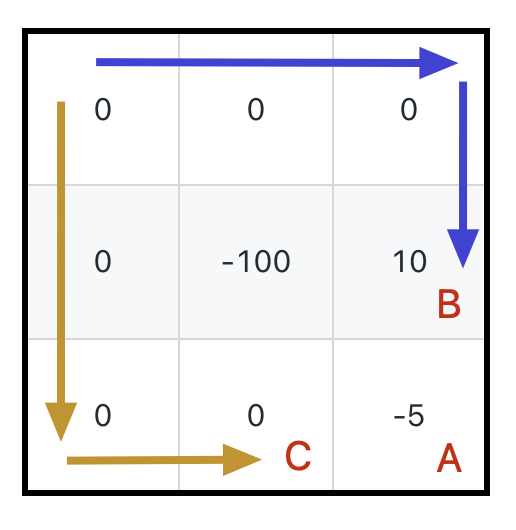
What do you think is the optimal path for the knight to rescue the princess in this scenario?

Clearly, it's to follow the blue line to B and then to A, right? This way, the initial health required is only 1. If you follow the yellow arrow path, first going to C and then to A, the initial health required would be at least 6.

Why is this the case? The minimum initial health to reach both B and C is 1. Why is the path from B to A preferred over C to A?

Because when the knight reaches B, the health level is 11, but when reaching C, it remains 1.

If the knight insists on going from C to A, the initial health must be increased to 6; but if from B to A, an initial health of 1 is sufficient because health potions picked up along the way provide enough health to withstand the damage from monsters above A.

This should be clear now. Reviewing our definition of the dp function, in the above scenario, the algorithm only knows that dp(1, 2) = dp(2, 1) = 1, which is the same. How can it make the right decision and compute dp(2, 2)?

Therefore, our previous definition of the dp array was incorrect; it lacked sufficient information for the algorithm to make correct state transitions.

The correct approach requires reverse thinking, still using the following dp function:

int dp(int[][] grid, int i, int j);

int dp(vector<vector<int>>& grid, int i, int j);

def dp(grid: List[List[int]], i: int, j: int) -> int:

func dp(grid [][]int, i int, j int) int {}

var dp = function(grid, i, j) {}

But we need to change the definition of the dp function:

The minimum health needed to go from grid[i][j] to the bottom-right corner is dp(grid, i, j).

We can write the code like this:

int calculateMinimumHP(int[][] grid) {
    // We want to calculate the minimum health value required
    // from the top-left corner to the bottom-right corner
    return dp(grid, 0, 0);
}

int dp(int[][] grid, int i, int j) {
    int m = grid.length;
    int n = grid[0].length;
    // base case
    if (i == m - 1 && j == n - 1) {
        return grid[i][j] >= 0 ? 1 : -grid[i][j] + 1;
    }
    ...
}

int calculateMinimumHP(vector<vector<int>>& grid) {
    // We want to calculate the minimum health required from
    // the top-left corner to the bottom-right corner
    return dp(grid, 0, 0);
}

int dp(vector<vector<int>>& grid, int i, int j) {
    int m = grid.size();
    int n = grid[0].size();
    // base case
    if (i == m - 1 && j == n - 1) {
        return grid[i][j] >= 0 ? 1 : -grid[i][j] + 1;
    }
    ...
}

def calculateMinimumHP(grid: List[List[int]]) -> int:
    # we want to calculate the minimum health value needed
    # from the top-left corner to the bottom-right corner
    return dp(grid, 0, 0)

def dp(grid: List[List[int]], i: int, j: int) -> int:
    m = len(grid)
    n = len(grid[0])
    # base case
    if i == m - 1 and j == n - 1:
        return 1 if grid[i][j] >= 0 else -grid[i][j] + 1
    ...

func calculateMinimumHP(grid [][]int) int {
    // We want to calculate the minimum health value required
    // from the top-left corner to the bottom-right corner
    return dp(grid, 0, 0)
}

func dp(grid [][]int, i int, j int) int {
    m := len(grid)
    n := len(grid[0])
    // base case
    if i == m-1 && j == n-1 {
        if grid[i][j] >= 0 {
            return 1
        } else {
            return -grid[i][j] + 1
        }
    }
    ...
}

// We want to calculate the minimum health required
// from the top-left corner to the bottom-right corner
var calculateMinimumHP = function(grid) {
    return dp(grid, 0, 0);
}

var dp = function(grid, i, j) {
    var m = grid.length;
    var n = grid[0].length;
    // base case
    if (i == m - 1 && j == n - 1) {
        return grid[i][j] >= 0 ? 1 : -grid[i][j] + 1;
    }
    ...
}

Based on this new definition and the base case, we want to find dp(0, 0). So we should use dp(i, j+1) and dp(i+1, j) to figure out dp(i, j), step by step, to get closer to the base case and do the state transition correctly.

More specifically, "the minimum health to reach the bottom-right from point A" should be decided by "the minimum health from B to the bottom-right" and "the minimum health from C to the bottom-right":

Can we figure it out? Yes. For example, if dp(0, 1) = 5 and dp(1, 0) = 4, it's better to go from A to C, because 4 is less than 5.

So how do we figure out the value for dp(0, 0)?

Suppose the value at A is 1. Since we know that the next step is to C, and dp(1, 0) = 4 means we need at least 4 health to reach grid[1][0], then at point A, the knight must have 4 - 1 = 3 health to continue.

If the value at A is 10, which means the knight goes up by 10 health right away, then 4 - 10 = -6, which is negative. But health should never be less than 1, otherwise the knight will die, so in this case, the required health is 1.

So we get the state transition formula:

int res = min(
    dp(i + 1, j),
    dp(i, j + 1)
) - grid[i][j];

dp(i, j) = res <= 0 ? 1 : res;

With this core logic and a memoization table to avoid overlapping subproblems, we can write the final code directly:

class Solution {

    public int calculateMinimumHP(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        // initialize the memo array with -1
        memo = new int[m][n];
        for (int[] row : memo) {
            Arrays.fill(row, -1);
        }

        return dp(grid, 0, 0);
    }

    // memo array to eliminate overlapping subproblems
    int[][] memo;

    // definition: the minimum initial health required
    // to reach the bottom-right corner from (i, j)
    int dp(int[][] grid, int i, int j) {
        int m = grid.length;
        int n = grid[0].length;
        // base case
        if (i == m - 1 && j == n - 1) {
            return grid[i][j] >= 0 ? 1 : -grid[i][j] + 1;
        }
        if (i == m || j == n) {
            return Integer.MAX_VALUE;
        }
        // avoid redundant calculations
        if (memo[i][j] != -1) {
            return memo[i][j];
        }
        // state transition logic
        int res = Math.min(
                dp(grid, i, j + 1),
                dp(grid, i + 1, j)
        ) - grid[i][j];
        // knight's health must be at least 1
        memo[i][j] = res <= 0 ? 1 : res;

        return memo[i][j];
    }
}

#include <vector>
#include <algorithm>
#include <climits>

using namespace std;

class Solution {

public:
    int calculateMinimumHP(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        // initialize the memo array with -1
        memo = vector<vector<int>>(m, vector<int>(n, -1));

        return dp(grid, 0, 0);
    }

private:
    // memo array to eliminate overlapping subproblems
    vector<vector<int>> memo;

    // definition: the minimum initial health required
    // to reach the bottom-right corner from (i, j)
    int dp(vector<vector<int>>& grid, int i, int j) {
        int m = grid.size();
        int n = grid[0].size();
        // base case
        if (i == m - 1 && j == n - 1) {
            return grid[i][j] >= 0 ? 1 : -grid[i][j] + 1;
        }
        if (i == m || j == n) {
            return INT_MAX;
        }
        // avoid redundant calculations
        if (memo[i][j] != -1) {
            return memo[i][j];
        }
        // state transition logic
        int res = min(
            dp(grid, i, j + 1),
            dp(grid, i + 1, j)
        ) - grid[i][j];
        // knight's health must be at least 1
        memo[i][j] = res <= 0 ? 1 : res;

        return memo[i][j];
    }
};

class Solution:

    def calculateMinimumHP(self, grid: List[List[int]]) -> int:
        m = len(grid)
        n = len(grid[0])
        # initialize the memo array with -1
        self.memo = [[-1] * n for _ in range(m)]

        return self.dp(grid, 0, 0)

    # memo array to eliminate overlapping subproblems
    memo = []

    # definition: the minimum initial health required
    # to reach the bottom-right corner from (i, j)
    def dp(self, grid: List[List[int]], i: int, j: int) -> int:
        m = len(grid)
        n = len(grid[0])
        # base case
        if i == m - 1 and j == n - 1:
            return 1 if grid[i][j] >= 0 else -grid[i][j] + 1
        if i == m or j == n:
            return float('inf')
        # avoid redundant calculations
        if self.memo[i][j] != -1:
            return self.memo[i][j]
        # state transition logic
        res = min(
            self.dp(grid, i, j + 1),
            self.dp(grid, i + 1, j)
        ) - grid[i][j]
        # knight's health must be at least 1
        self.memo[i][j] = 1 if res <= 0 else res

        return self.memo[i][j]

import (
	"math"
)

func calculateMinimumHP(grid [][]int) int {
	m := len(grid)
	n := len(grid[0])
	// initialize the memo array with -1
	memo := make([][]int, m)
	for i := range memo {
		memo[i] = make([]int, n)
		for j := range memo[i] {
			memo[i][j] = -1
		}
	}

	return dp(grid, 0, 0, memo)
}

// memo array to eliminate overlapping subproblems
// definition: the minimum initial health required to reach the bottom-right corner from (i, j)
func dp(grid [][]int, i, j int, memo [][]int) int {
	m := len(grid)
	n := len(grid[0])
	// base case
	if i == m-1 && j == n-1 {
		if grid[i][j] >= 0 {
			return 1
		}
		return -grid[i][j] + 1
	}
	if i >= m || j >= n {
		// Out of bounds, return a large number that represents impossible to proceed
		return math.MaxInt32
	}
	// avoid redundant calculations
	if memo[i][j] != -1 {
		return memo[i][j]
	}
	// state transition logic
	right := dp(grid, i, j+1, memo)
	down := dp(grid, i+1, j, memo)
	res := int(math.Min(float64(right), float64(down))) - grid[i][j]
	// knight's health must be at least 1
	memo[i][j] = max(res, 1)

	return memo[i][j]
}

// Helper function to return the maximum of two integers.
func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

var calculateMinimumHP = function(grid) {
    let m = grid.length;
    let n = grid[0].length;
    // initialize the memo array with -1
    let memo = Array.from({ length: m }, () => Array(n).fill(-1));

    return dp(grid, 0, 0, memo);
};

// memo array to eliminate overlapping subproblems
// definition: the minimum initial health required to reach the bottom-right corner from (i, j)
// @visualize status(i,j)
var dp = function(grid, i, j, memo) {
    let m = grid.length;
    let n = grid[0].length;
    // base case
    if (i == m - 1 && j == n - 1) {
        return grid[i][j] >= 0 ? 1 : -grid[i][j] + 1;
    }
    if (i == m || j == n) {
        return Number.MAX_SAFE_INTEGER;
    }
    // avoid redundant calculations
    if (memo[i][j] != -1) {
        return memo[i][j];
    }
    // state transition logic
    let res = Math.min(
        dp(grid, i, j + 1, memo),
        dp(grid, i + 1, j, memo)
    ) - grid[i][j];
    // knight's health must be at least 1
    memo[i][j] = res <= 0 ? 1 : res;

    return memo[i][j];
};

This is the top-down dynamic programming solution with memoization. You can check the previous article Dynamic Programming Pattern Explained to see how to write the iterative version with a dp array.

We can define the dp array like this:

The minimum health needed from grid[i][j] to the bottom-right is dp[i][j].

The base case is dp[m-1][n-1] = 1, that is, standing at the goal, the knight needs at least 1 health.

From each cell grid[i][j], you can go either right or down, so the state transition formula is:

dp[i][j] = Math.min(dp[i + 1][j], dp[i][j + 1]) - grid[i][j];

The value of dp[i][j] depends on the cell below (dp[i+1][j]) and to the right (dp[i][j+1]). So we first need to fill in the last row dp[n-1][..] and last column dp[..][m-1], and then fill the rest from bottom to top and right to left:

class Solution {

    public int calculateMinimumHP(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        final int INF = Integer.MAX_VALUE / 2;
        // dp[i][j] is the minimum initial health to reach bottom-right from (i, j)
        int[][] dp = new int[m][n];

        // base case, bottom-right needs at least 1 health
        dp[m - 1][n - 1] = Math.max(1, 1 - grid[m - 1][n - 1]);

        // last column
        for (int i = m - 2; i >= 0; i--) {
            int need = dp[i + 1][n - 1] - grid[i][n - 1];
            dp[i][n - 1] = need <= 0 ? 1 : need;
        }
        // last row
        for (int j = n - 2; j >= 0; j--) {
            int need = dp[m - 1][j + 1] - grid[m - 1][j];
            dp[m - 1][j] = need <= 0 ? 1 : need;
        }

        // fill the rest bottom-up, right-to-left
        for (int i = m - 2; i >= 0; i--) {
            for (int j = n - 2; j >= 0; j--) {
                int down = dp[i + 1][j];
                int right = dp[i][j + 1];
                int need = Math.min(down, right) - grid[i][j];
                dp[i][j] = need <= 0 ? 1 : need;
            }
        }

        return dp[0][0];
    }
}

class Solution {

public:
    int calculateMinimumHP(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        const int INF = INT_MAX / 2;
        // dp[i][j] is the minimum initial health to reach bottom-right from (i, j)
        vector<vector<int>> dp(m, vector<int>(n, INF));

        // base case, bottom-right needs at least 1 health
        dp[m - 1][n - 1] = max(1, 1 - grid[m - 1][n - 1]);

        // last column
        for (int i = m - 2; i >= 0; i--) {
            int need = dp[i + 1][n - 1] - grid[i][n - 1];
            dp[i][n - 1] = need <= 0 ? 1 : need;
        }
        // last row
        for (int j = n - 2; j >= 0; j--) {
            int need = dp[m - 1][j + 1] - grid[m - 1][j];
            dp[m - 1][j] = need <= 0 ? 1 : need;
        }

        // fill the rest bottom-up, right-to-left
        for (int i = m - 2; i >= 0; i--) {
            for (int j = n - 2; j >= 0; j--) {
                int need = min(dp[i + 1][j], dp[i][j + 1]) - grid[i][j];
                dp[i][j] = need <= 0 ? 1 : need;
            }
        }

        return dp[0][0];
    }
};

from typing import List


class Solution:

    def calculateMinimumHP(self, grid: List[List[int]]) -> int:
        m = len(grid)
        n = len(grid[0])
        INF = 10**18
        # dp[i][j] is the minimum initial health to reach bottom-right from (i, j)
        dp = [[INF] * n for _ in range(m)]

        # base case, bottom-right needs at least 1 health
        dp[m - 1][n - 1] = max(1, 1 - grid[m - 1][n - 1])

        # last column
        for i in range(m - 2, -1, -1):
            need = dp[i + 1][n - 1] - grid[i][n - 1]
            dp[i][n - 1] = 1 if need <= 0 else need
        # last row
        for j in range(n - 2, -1, -1):
            need = dp[m - 1][j + 1] - grid[m - 1][j]
            dp[m - 1][j] = 1 if need <= 0 else need

        # fill the rest bottom-up, right-to-left
        for i in range(m - 2, -1, -1):
            for j in range(n - 2, -1, -1):
                need = min(dp[i + 1][j], dp[i][j + 1]) - grid[i][j]
                dp[i][j] = 1 if need <= 0 else need

        return dp[0][0]

import "math"

func calculateMinimumHP(grid [][]int) int {
    m := len(grid)
    n := len(grid[0])
    // dp[i][j] is the minimum initial health to reach bottom-right from (i, j)
    dp := make([][]int, m)
    for i := range dp {
        dp[i] = make([]int, n)
        for j := range dp[i] {
            dp[i][j] = math.MaxInt32 / 2
        }
    }

    // base case, bottom-right needs at least 1 health
    dp[m-1][n-1] = max(1, 1-grid[m-1][n-1])

    // last column
    for i := m - 2; i >= 0; i-- {
        need := dp[i+1][n-1] - grid[i][n-1]
        dp[i][n-1] = max(1, need)
    }
    // last row
    for j := n - 2; j >= 0; j-- {
        need := dp[m-1][j+1] - grid[m-1][j]
        dp[m-1][j] = max(1, need)
    }

    // fill the rest bottom-up, right-to-left
    for i := m - 2; i >= 0; i-- {
        for j := n - 2; j >= 0; j-- {
            need := min(dp[i+1][j], dp[i][j+1]) - grid[i][j]
            dp[i][j] = max(1, need)
        }
    }

    return dp[0][0]
}

func min(a, b int) int {
    if a < b {
        return a
    }
    return b
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

var calculateMinimumHP = function(grid) {
    const m = grid.length;
    const n = grid[0].length;
    const INF = Number.MAX_SAFE_INTEGER;
    // dp[i][j] is the minimum initial health to reach bottom-right from (i, j)
    const dp = Array.from({ length: m }, () => Array(n).fill(INF));

    // base case, bottom-right needs at least 1 health
    dp[m - 1][n - 1] = Math.max(1, 1 - grid[m - 1][n - 1]);

    // last column
    for (let i = m - 2; i >= 0; i--) {
        const need = dp[i + 1][n - 1] - grid[i][n - 1];
        dp[i][n - 1] = need <= 0 ? 1 : need;
    }
    // last row
    for (let j = n - 2; j >= 0; j--) {
        const need = dp[m - 1][j + 1] - grid[m - 1][j];
        dp[m - 1][j] = need <= 0 ? 1 : need;
    }

    // fill the rest bottom-up, right-to-left
    for (let i = m - 2; i >= 0; i--) {
        for (let j = n - 2; j >= 0; j--) {
            const need = Math.min(dp[i + 1][j], dp[i][j + 1]) - grid[i][j];
            dp[i][j] = need <= 0 ? 1 : need;
        }
    }

    return dp[0][0];
};

This completes the dynamic programming solution for this problem. The hardest part is to define the dp function. Once you do that, you can find the correct state transition and get the right answer.