How to Design Transition Equations
This article will resolve
| LeetCode | Difficulty |
|---|---|
| 300. Longest Increasing Subsequence | 🟠 |
| 300. Longest Increasing Subsequence | 🟠 |
| 354. Russian Doll Envelopes | 🔴 |
Prerequisite Knowledge
Before reading this article, you should first learn:
Some readers may have read the previous article Detailed Explanation of Dynamic Programming and learned the dynamic programming approach: identifying the "state" of the problem, clarifying the meaning of the dp array/function, and defining the base case. However, they might still struggle with determining the "choices," or finding the state transition relationship, and thus fail to write a dynamic programming solution. What should they do?
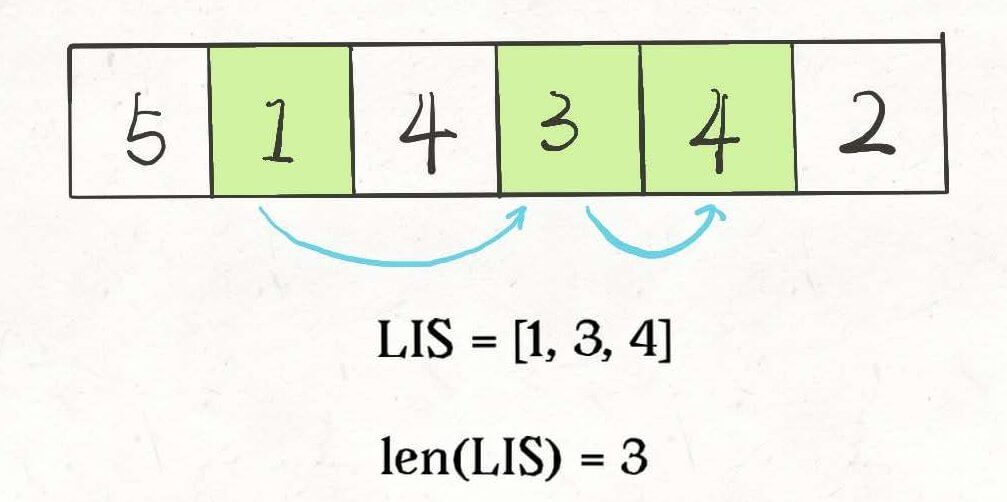
Do not worry. The difficulty of dynamic programming lies in finding the correct state transition equation. This article will use the classic "Longest Increasing Subsequence Problem" to explain general techniques for designing dynamic programming solutions: Mathematical Induction.
The Longest Increasing Subsequence (LIS) is a classic algorithm problem. A straightforward approach is the dynamic programming solution, with a time complexity of O(N^2). We will use this problem to explain step-by-step how to find the state transition equation and write a dynamic programming solution. A less obvious approach uses binary search, with a time complexity of O(NlogN), which we will understand through a simple card game to grasp this clever solution.
LeetCode Problem 300, "Longest Increasing Subsequence," addresses this problem:
300. Longest Increasing Subsequence | LeetCode | 🟠
Given an integer array nums, return the length of the longest strictly increasing subsequence.
Example 1:
Input: nums = [10,9,2,5,3,7,101,18] Output: 4 Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.
Example 2:
Input: nums = [0,1,0,3,2,3] Output: 4
Example 3:
Input: nums = [7,7,7,7,7,7,7] Output: 1
Constraints:
1 <= nums.length <= 2500-104 <= nums[i] <= 104
Follow up: Can you come up with an algorithm that runs in O(n log(n)) time complexity?
// Function signature
int lengthOfLIS(int[] nums);// function signature
int lengthOfLIS(vector<int>& nums);# Function signature
def lengthOfLIS(nums: List[int]) -> int:// function signature
func lengthOfLIS(nums []int) int {}// Function signature
var lengthOfLIS = function(nums) {}For example, given the input nums=[10,9,2,5,3,7,101,18], the longest increasing subsequence is [2,3,7,101], so the algorithm should output 4.
Note the difference between the terms "subsequence" and "substring": a substring must be continuous, while a subsequence does not have to be continuous. Let's first design a dynamic programming algorithm to solve this problem.
I. Dynamic Programming Solution
The core design idea of dynamic programming is mathematical induction.
Everyone should be familiar with mathematical induction, as it is taught in high school and the concept is straightforward. For instance, if we want to prove a mathematical statement, we first assume that the statement holds for k < n, and then based on this assumption, we try to derive and prove that the statement also holds for k = n. If we can prove this, then the statement is valid for any value of k.
Similarly, when designing a dynamic programming algorithm, we need a dp array, right? We can assume that dp[0...i-1] has already been calculated, and then ask ourselves: how can we use these results to calculate dp[i]?
Taking the longest increasing subsequence problem as an example will make this clear. However, first, we need to clearly define what the dp array represents, i.e., what does the value of dp[i] signify?
Our definition is as follows: dp[i] represents the length of the longest increasing subsequence ending with nums[i].
Info
Why define it this way? This is a common approach to solving subsequence problems, and the article Dynamic Programming for Subsequence Problems Template summarizes several common approaches. After reading all the dynamic programming problems in this chapter, you will find that there are only a few ways to define the dp array.
Based on this definition, we can derive the base case: the initial value of dp[i] is 1, because the longest increasing subsequence ending with nums[i] must at least include itself.
Here are two examples:
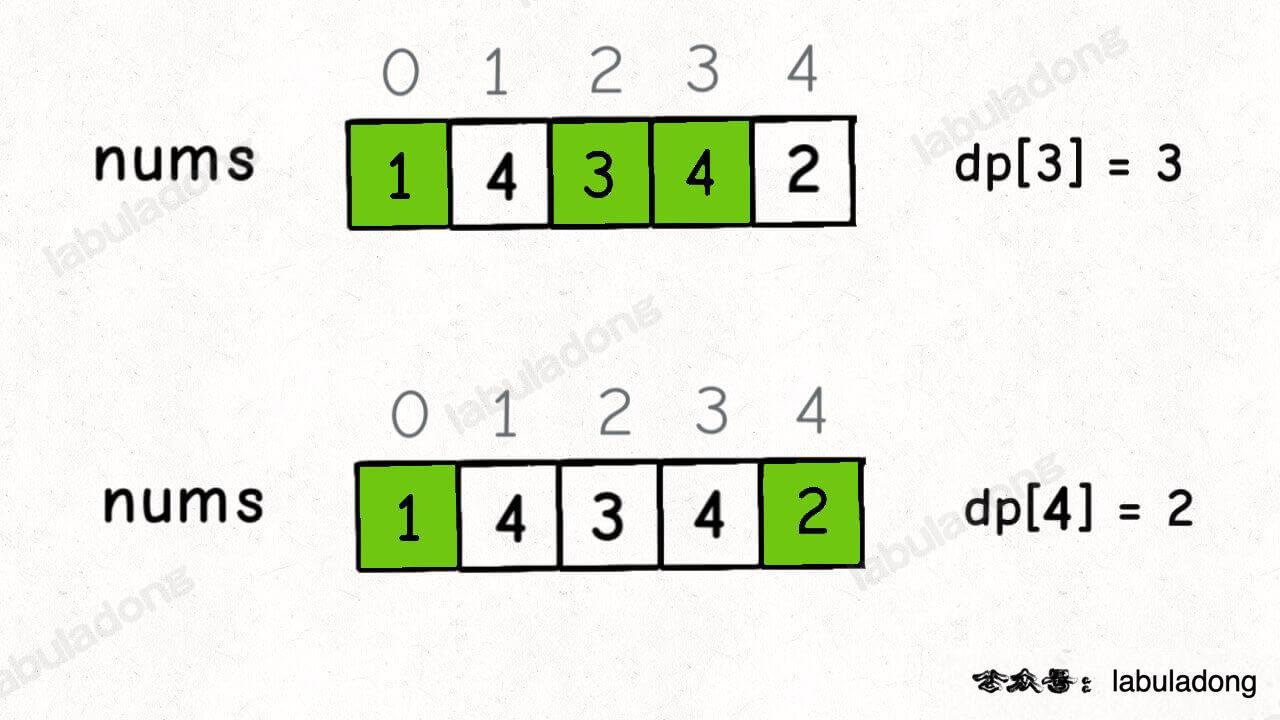
This GIF illustrates the evolution of the algorithm:
According to this definition, our final result (the maximum length of the subsequence) should be the maximum value in the dp array.
int res = 0;
for (int i = 0; i < dp.length; i++) {
res = Math.max(res, dp[i]);
}
return res;Readers might wonder, in the earlier algorithm progression, each result of dp[i] was observed with the naked eye. How should we design the algorithm logic to correctly compute each dp[i]?
This is the essence of dynamic programming: how to design the algorithm logic for state transitions to ensure correct execution. Here, we need to use the concept of mathematical induction:
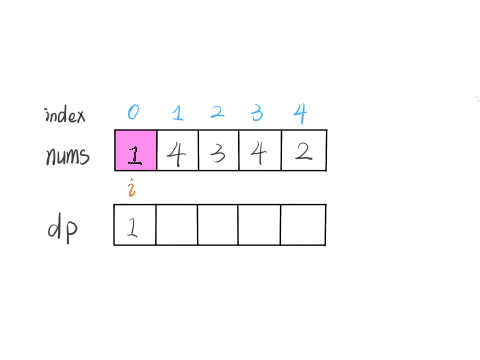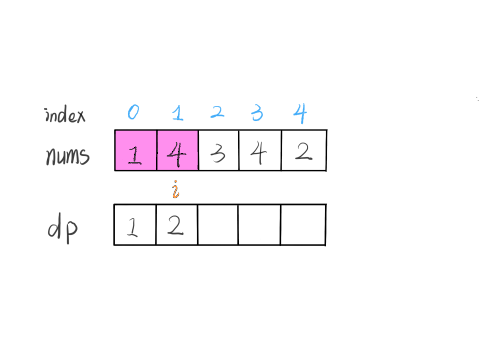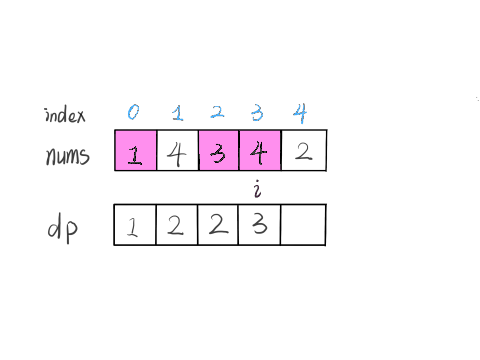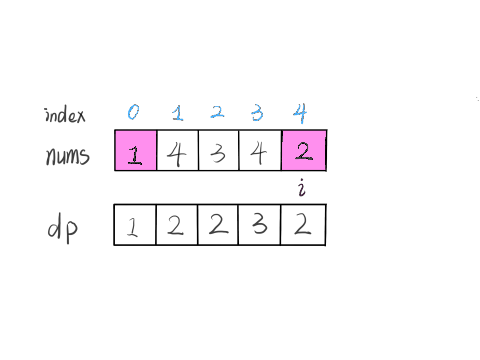
Assuming we already know all the results of dp[0..4], how can we derive dp[5] from these known results?

Based on our previous definition of the dp array, we now want to find the value of dp[5], which means we want the longest increasing subsequence ending with nums[5].
nums[5] = 3. Since it is an increasing subsequence, we just need to find the subsequences ending with elements smaller than 3, and then append 3 to the end of these subsequences to form a new increasing subsequence. The length of this new subsequence will increase by one.
Which elements before nums[5] are smaller than nums[5]? This is straightforward to calculate; a for loop can be used to compare and find these elements.
What is the length of the longest increasing subsequence ending with these elements? Let's recall our definition of the dp array, which records the length of the longest increasing subsequence ending with each element.
In our example, nums[0] and nums[4] are both smaller than nums[5]. By comparing the values of dp[0] and dp[4], we combine nums[5] with the longer increasing subsequence to get dp[5] = 3:
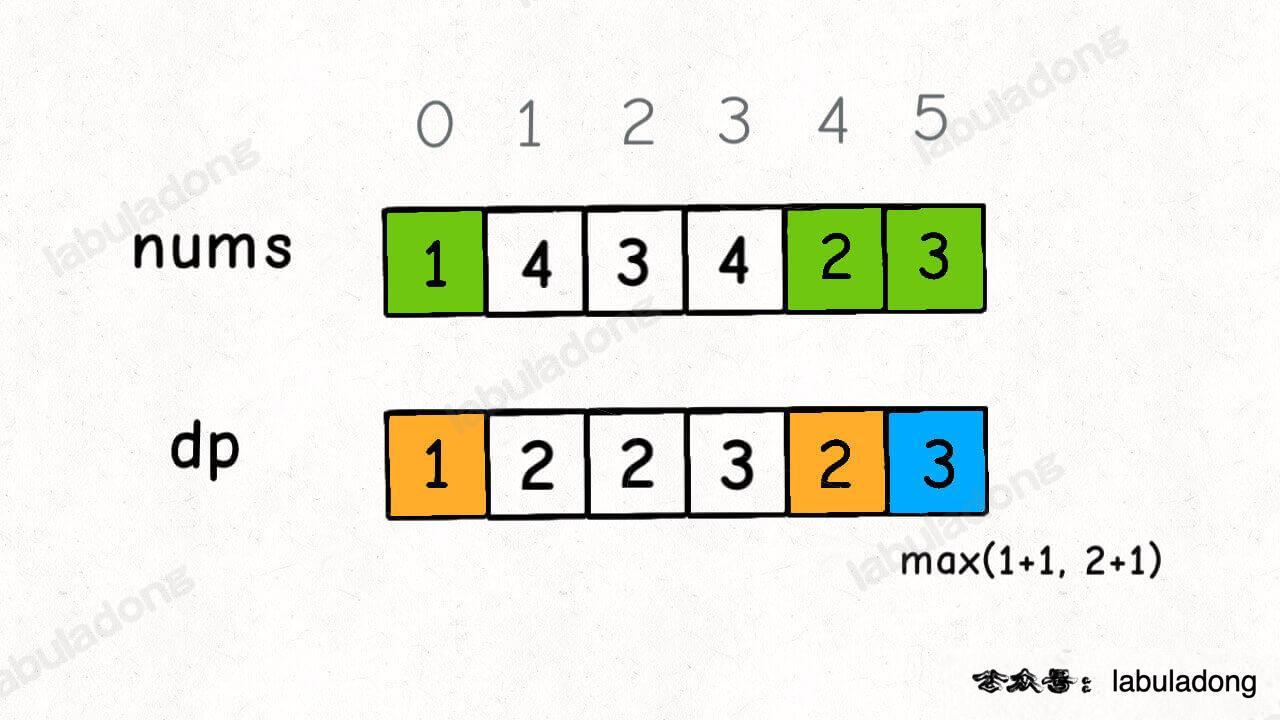
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}When i = 5, this code logic can calculate dp[5]. In fact, at this point, we have basically solved this algorithm problem.
Readers might wonder, we just calculated dp[5], how do we calculate dp[4], dp[3], and others? Similar to mathematical induction, once you can calculate dp[5], you can calculate the rest:
for (int i = 0; i < nums.length; i++) {
for (int j = 0; j < i; j++) {
// find elements in nums[0..i-1] that are smaller than nums[i]
if (nums[i] > nums[j]) {
// append nums[i] to the end, forming a subsequence of length dp[j] + 1,
// and it is an increasing subsequence ending with nums[i]
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}Combining the base case we just discussed, let's take a look at the complete code:
class Solution {
public int lengthOfLIS(int[] nums) {
// dp[i] represents the length of the longest increasing subsequence ending with nums[i]
int[] dp = new int[nums.length]; // base case: initialize all elements of the dp array to 1
Arrays.fill(dp, 1);
for (int i = 0; i < nums.length; i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j])
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
int res = 0;
for (int i = 0; i < dp.length; i++) {
res = Math.max(res, dp[i]);
}
return res;
}
}
// base case: initialize all elements of the dp array to 1
Arrays.fill(dp, 1);
for (int i = 0; i < nums.length; i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j])
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
int res = 0;
for (int i = 0; i < dp.length; i++) {
res = Math.max(res, dp[i]);
}
return res;
}
}class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
// Definition: dp[i] represents the length of the
// longest increasing subsequence ending with nums[i]
vector<int> dp(nums.size());
// base case: initialize all elements of dp array to 1
fill(dp.begin(), dp.end(), 1);
for (int i = 0; i < nums.size(); i++) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
dp[i] = max(dp[i], dp[j] + 1); }
}
}
int res = 0;
for (int i = 0; i < dp.size(); i++) {
res = max(res, dp[i]);
}
return res;
}
};
}
}
}
int res = 0;
for (int i = 0; i < dp.size(); i++) {
res = max(res, dp[i]);
}
return res;
}
};class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
# Definition: dp[i] represents the length of the
# longest increasing subsequence ending with nums[i]
dp = [1]*len(nums)
# base case: initialize all elements of dp array to 1
for i in range(len(nums)):
for j in range(i):
if nums[i] > nums[j]:
dp[i] = max(dp[i], dp[j] + 1)  res = 0
for i in range(len(dp)):
res = max(res, dp[i])
return res
res = 0
for i in range(len(dp)):
res = max(res, dp[i])
return resfunc lengthOfLIS(nums []int) int {
// Definition: dp[i] represents the length of the
// longest increasing subsequence ending with nums[i]
dp := make([]int, len(nums))
// base case: initialize all elements of dp array to 1
for i := range dp {
dp[i] = 1
}
for i := 0; i < len(nums); i++ {
for j := 0; j < i; j++ {
if nums[i] > nums[j] {
// dp[i] = Math.max(dp[i], dp[j] + 1);
dp[i] = max(dp[i], dp[j] + 1); }
}
}
res := 0
for i := 0; i < len(dp); i++ {
res = max(res, dp[i])
}
return res
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
}
}
}
res := 0
for i := 0; i < len(dp); i++ {
res = max(res, dp[i])
}
return res
}
func max(a, b int) int {
if a > b {
return a
}
return b
}var lengthOfLIS = function(nums) {
// Definition: dp[i] represents the length of the
// longest increasing subsequence ending with nums[i]
let dp = new Array(nums.length).fill(1);
// base case: initialize all elements of the dp array to 1
for (let i = 0; i < nums.length; i++) {
for (let j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j] + 1); }
}
}
let res = 0;
for (let i = 0; i < dp.length; i++) {
res = Math.max(res, dp[i]);
}
return res;
};
}
}
}
let res = 0;
for (let i = 0; i < dp.length; i++) {
res = Math.max(res, dp[i]);
}
return res;
};Algorithm Visualization
At this point, the problem is solved with a time complexity of . Here is a summary of how to determine the state transition relation in dynamic programming:
Clearly define the
dparray. This step is crucial for any dynamic programming problem. If the definition is inappropriate or unclear, it can hinder subsequent steps.Based on the definition of the
dparray, use the principle of mathematical induction. Assumedp[0...i-1]is known, and find a way to determinedp[i]. Once this step is completed, the problem is essentially solved.
However, if this step cannot be completed, it may indicate that the definition of the dp array is not appropriate and needs redefining. Alternatively, it might mean that the information stored in the dp array is insufficient to deduce the next answer, necessitating an expansion of the dp array into a two-dimensional or even three-dimensional array.
The current solution follows the standard dynamic programming approach, but for the longest increasing subsequence problem, this method may not be optimal and might not pass all test cases. A more efficient solution will be discussed below.
2. Binary Search Approach
This solution has a time complexity of . To be honest, it's not a method that most people would think of (though perhaps those who have played certain card games might come up with it). It's good to be aware of it, but in most cases, providing a dynamic programming solution is already quite commendable.
Based on the problem's description, it is hard to imagine how this issue could be related to binary search. In fact, the longest increasing subsequence problem is related to a card game known as patience game. There is even a sorting method called patience sorting.
For simplicity, we will skip all mathematical proofs and use a simplified example to understand the algorithm's concept.
First, imagine you have a row of playing cards. We process these cards one by one from left to right, just like traversing an array, and ultimately divide them into several piles.
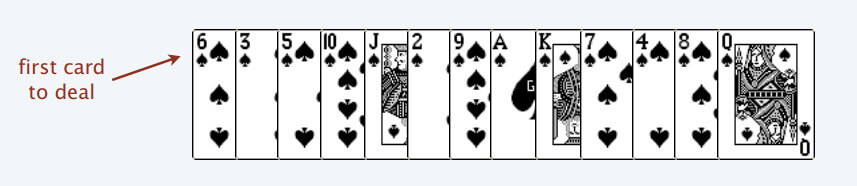
The rules for handling these playing cards are as follows:
- You can only place a card with a smaller value on top of a card with a larger value.
- If there is no pile where the current card can be placed due to its larger value, create a new pile and place the card there.
- If the current card can be placed on multiple piles, choose the leftmost pile.
For example, the aforementioned cards will ultimately be divided into 5 piles (we consider the Ace to have the highest value and the 2 to have the lowest value).
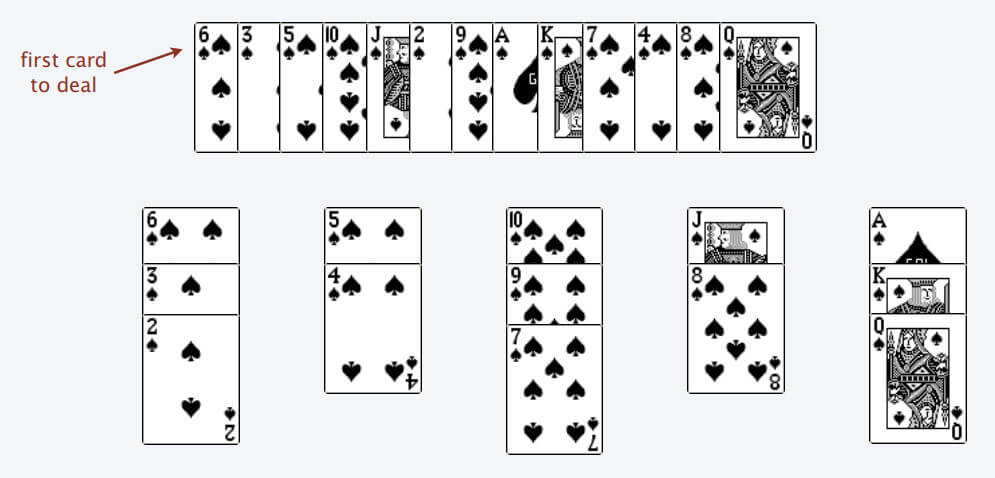
Why place the card on the leftmost pile when multiple options are available? This ensures that the top cards of the piles are in order (2, 4, 7, 8, Q), proof omitted.
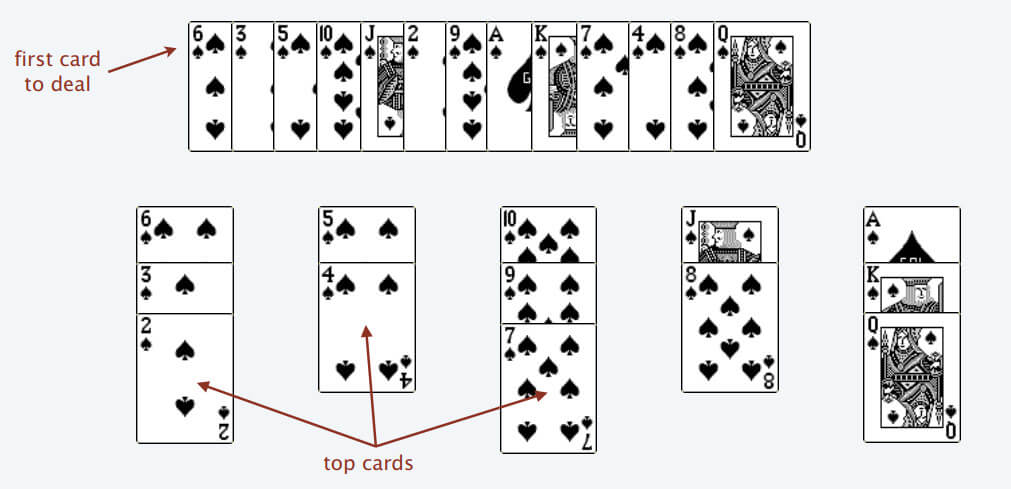
Following these rules, you can determine the longest increasing subsequence. The number of piles corresponds to the length of the longest increasing subsequence, proof omitted.
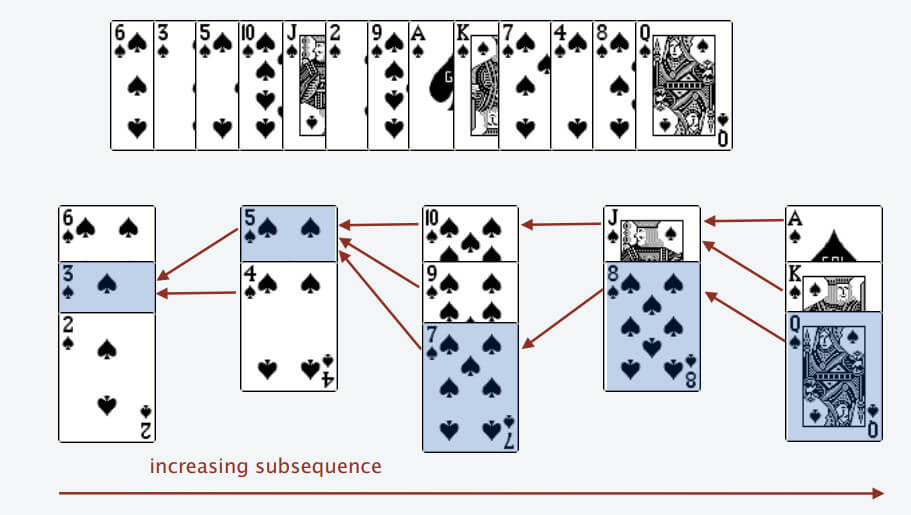
We simply need to program the process of handling the cards. Each time a card is processed, we need to find a suitable pile top to place it. Since the top cards of the piles are sorted, binary search can be applied: use binary search to find the appropriate position for the current card.
Tip
The previous article Binary Search Algorithm Detailed Explanation provides a thorough introduction to the details and variants of binary search. It is perfectly applicable here, and if you haven't read it, we strongly recommend doing so.
class Solution {
public int lengthOfLIS(int[] nums) {
int[] top = new int[nums.length];
// initialize the number of piles to 0
int piles = 0;
for (int i = 0; i < nums.length; i++) {
// the poker card to be processed
int poker = nums[i];
// ***** binary search for the left boundary *****
int left = 0, right = piles;
while (left < right) {
int mid = (left + right) / 2;
if (top[mid] > poker) {
right = mid;
} else if (top[mid] < poker) {
left = mid + 1;
} else {
right = mid;
}
}
// *********************************
// no suitable pile found, create a new pile
if (left == piles) piles++;
// place this card on the top of the pile
top[left] = poker;
}
// the number of piles is the length of LIS
return piles;
}
}class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
vector<int> top(nums.size());
// initialize the number of piles to 0
int piles = 0;
for (int i = 0; i < nums.size(); i++) {
// the card to be processed
int poker = nums[i];
// ***** binary search for the left boundary *****
int left = 0, right = piles;
while (left < right) {
int mid = (left + right) / 2;
if (top[mid] > poker) {
right = mid;
} else if (top[mid] < poker) {
left = mid + 1;
} else {
right = mid;
}
}
// ********************************
// no suitable pile found, create a new one
if (left == piles) piles++;
// place this card on the top of the pile
top[left] = poker;
}
// the number of piles is the length of LIS
return piles;
}
};class Solution:
def lengthOfLIS(self, nums):
top = [0] * len(nums)
# initialize the number of piles to 0
piles = 0
for i in range(len(nums)):
# the poker card to be processed
poker = nums[i]
# binary search for the left boundary
left, right = 0, piles
while left < right:
mid = (left + right) // 2
if top[mid] > poker:
right = mid
elif top[mid] < poker:
left = mid + 1
else:
right = mid
# no suitable pile found, create a new one
if left == piles:
piles += 1
# place this card on top of the pile
top[left] = poker
# the number of piles is the length of LIS
return pilesfunc lengthOfLIS(nums []int) int {
top := make([]int, len(nums))
// initialize the number of piles to 0
var piles int
for i := 0; i < len(nums); i++ {
// the poker card to be processed
poker := nums[i]
// ***** binary search for the left boundary *****
var left, right int = 0, piles
for left < right {
mid := (left + right) / 2
if top[mid] > poker {
right = mid
} else if top[mid] < poker {
left = mid + 1
} else {
right = mid
}
}
// ********************************
// no suitable pile found, create a new one
if left == piles {
piles++
}
// place this card on the top of the pile
top[left] = poker
}
// the number of piles is the length of LIS
return piles
}var lengthOfLIS = function(nums) {
var top = new Array(nums.length);
// initialize the number of piles to 0
var piles = 0;
for (var i = 0; i < nums.length; i++) {
// the poker card to be processed
var poker = nums[i];
// ***** binary search for the left boundary *****
var left = 0, right = piles;
while (left < right) {
var mid = Math.floor((left + right) / 2);
if (top[mid] > poker) {
right = mid;
} else if (top[mid] < poker) {
left = mid + 1;
} else {
right = mid;
}
}
// ********************************
// no suitable pile found, create a new one
if (left == piles) piles++;
// place this card on the top of the pile
top[left] = poker;
}
// the number of piles is the length of LIS
return piles;
};Algorithm Visualization
Here, the explanation of the binary search solution is complete.
This solution is indeed hard to come up with. First, it involves mathematical proof. Who would think that following these rules would yield the longest increasing subsequence? Second, it requires the application of binary search. If you're not clear on the details of binary search, even with the idea, it's hard to implement correctly.
Therefore, consider this method as a mental exercise. However, the design approach of dynamic programming should be fully understood: assume the previous answers are known, use mathematical induction to correctly deduce and transition states, and ultimately arrive at the solution.
3. Extending to Two Dimensions
Let's examine an interesting problem frequently encountered in life, LeetCode Problem 354: "Russian Doll Envelopes". Here's the problem description:
354. Russian Doll Envelopes | LeetCode | 🔴
You are given a 2D array of integers envelopes where envelopes[i] = [wi, hi] represents the width and the height of an envelope.
One envelope can fit into another if and only if both the width and height of one envelope are greater than the other envelope's width and height.
Return the maximum number of envelopes you can Russian doll (i.e., put one inside the other).
Note: You cannot rotate an envelope.
Example 1:
Input: envelopes = [[5,4],[6,4],[6,7],[2,3]]
Output: 3
Explanation: The maximum number of envelopes you can Russian doll is 3 ([2,3] => [5,4] => [6,7]).
Example 2:
Input: envelopes = [[1,1],[1,1],[1,1]] Output: 1
Constraints:
1 <= envelopes.length <= 105envelopes[i].length == 21 <= wi, hi <= 105
This problem is essentially a variation of the Longest Increasing Subsequence (LIS) problem. Since each valid nesting involves a larger envelope enveloping a smaller one, it's akin to finding the longest increasing subsequence on a two-dimensional plane, where the length represents the maximum number of nested envelopes.
The standard LIS algorithm can only find the longest subsequence in a one-dimensional array, while our envelopes are represented in the form of two-dimensional pairs (w, h). How can we apply the LIS algorithm in this context?
One might think of calculating the area using w × h and then applying the standard LIS algorithm to the area. However, a little consideration reveals this approach is flawed. For example, 1 × 10 is greater than 3 × 3, but clearly, such envelopes cannot nest within each other.
The solution to this problem is quite ingenious:
First, sort the widths w in ascending order. If there are ties in w, then sort the heights h in descending order. After that, treat all h as an array and calculate the length of the Longest Increasing Subsequence (LIS) on this array, which will be the answer.
To better understand, let's visualize it by first sorting these pairs:
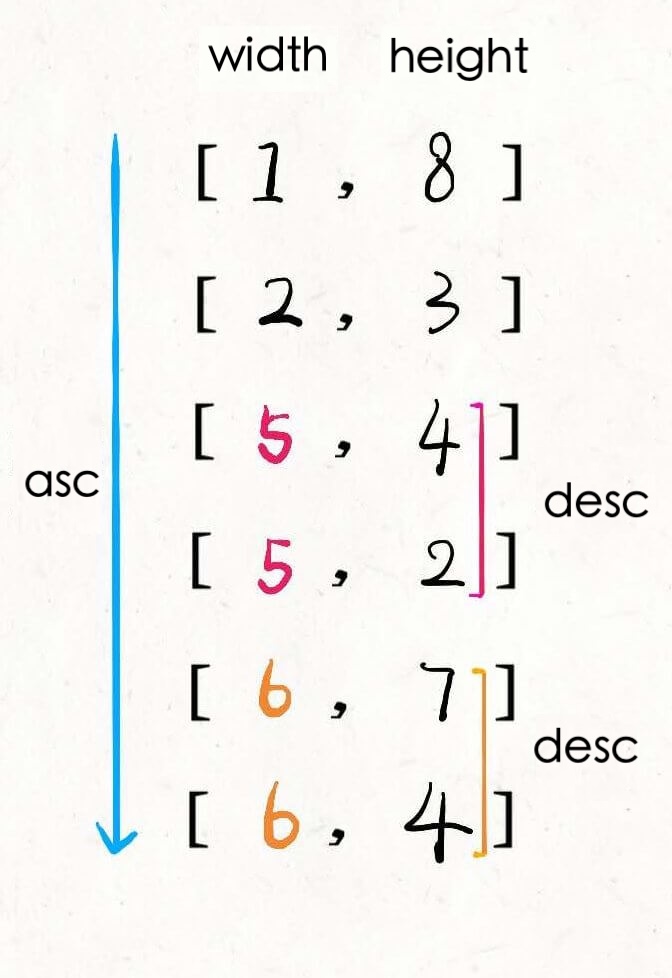
Then, find the Longest Increasing Subsequence on the h values. This subsequence represents the optimal nesting scheme:

Why does this approach find the sequence of envelopes that can be nested within each other? A bit of thought will make it clear:
Firstly, sorting the widths w in ascending order ensures that the w dimension can be nested. Thus, we only need to focus on the h dimension being able to nest.
Secondly, envelopes with the same width w cannot contain each other. Therefore, for envelopes with the same width w, we sort the heights h in descending order to ensure that there are no multiple envelopes with the same w in the two-dimensional LIS (as the problem states that identical dimensions cannot be nested).
Here is the code for the solution:
class Solution {
public int maxEnvelopes(int[][] envelopes) {
int n = envelopes.length;
// Sort by width in ascending order, and if widths are
// the same, sort by height in descending order
Arrays.sort(envelopes, new Comparator<int[]>()
{
public int compare(int[] a, int[] b) {
return a[0] == b[0] ?
b[1] - a[1] : a[0] - b[0];
}
});
// Find the LIS for the height array
int[] height = new int[n];
for (int i = 0; i < n; i++)
height[i] = envelopes[i][1];
return lengthOfLIS(height);
}
// Return the length of the LIS in nums
public int lengthOfLIS(int[] nums) {
int piles = 0, n = nums.length;
int[] top = new int[n];
for (int i = 0; i < n; i++) {
// The poker card to be processed
int poker = nums[i];
int left = 0, right = piles;
// Binary search for the insertion position
while (left < right) {
int mid = (left + right) / 2;
if (top[mid] >= poker)
right = mid;
else
left = mid + 1;
}
if (left == piles) piles++;
// Place this card on the top of the pile
top[left] = poker;
}
// The number of piles is the length of the LIS
return piles;
}
}#include <vector>
#include <algorithm>
class Solution {
public:
int maxEnvelopes(std::vector<std::vector<int>>& envelopes) {
int n = envelopes.size();
// Sort by width in ascending order, and if widths are
// the same, sort by height in descending order
std::sort(envelopes.begin(), envelopes.end(), [](const std::vector<int>& a, const std::vector<int>& b) {
return a[0] == b[0] ? b[1] < a[1] : a[0] < b[0];
});
// Find the LIS for the height array
std::vector<int> height(n);
for (int i = 0; i < n; i++)
height[i] = envelopes[i][1];
return lengthOfLIS(height);
}
// Return the length of the LIS in nums
int lengthOfLIS(std::vector<int>& nums) {
int piles = 0, n = nums.size();
std::vector<int> top(n);
for (int i = 0; i < n; i++) {
// The poker card to be processed
int poker = nums[i];
int left = 0, right = piles;
// Binary search for the insertion position
while (left < right) {
int mid = (left + right) / 2;
if (top[mid] >= poker)
right = mid;
else
left = mid + 1;
}
if (left == piles) piles++;
// Place this card on the top of the pile
top[left] = poker;
}
// The number of piles is the length of the LIS
return piles;
}
};class Solution:
def maxEnvelopes(self, envelopes: List[List[int]]) -> int:
n = len(envelopes)
# Sort by width in ascending order, and if widths are
# the same, sort by height in descending order
envelopes.sort(key=lambda x: (x[0], -x[1]))
# Find the LIS for the height array
height = [envelopes[i][1] for i in range(n)]
return self.lengthOfLIS(height)
# Return the length of the LIS in nums
def lengthOfLIS(self, nums: List[int]) -> int:
piles = 0
n = len(nums)
top = [0] * n
for i in range(n):
# The poker card to be processed
poker = nums[i]
left, right = 0, piles
# Binary search for the insertion position
while left < right:
mid = (left + right) // 2
if top[mid] >= poker:
right = mid
else:
left = mid + 1
if left == piles: piles += 1
# Place this card on the top of the pile
top[left] = poker
# The number of piles is the length of the LIS
return pilesfunc maxEnvelopes(envelopes [][]int) int {
n := len(envelopes)
// Sort by width in ascending order, and if widths are
// the same, sort by height in descending order
sort.Slice(envelopes, func(i, j int) bool {
if envelopes[i][0] == envelopes[j][0] {
return envelopes[i][1] > envelopes[j][1]
}
return envelopes[i][0] < envelopes[j][0]
})
// Find the LIS for the height array
height := make([]int, n)
for i := 0; i < n; i++ {
height[i] = envelopes[i][1]
}
return lengthOfLIS(height)
}
// Return the length of the LIS in nums
func lengthOfLIS(nums []int) int {
piles := 0
n := len(nums)
top := make([]int, n)
for _, poker := range nums {
// The poker card to be processed
left, right := 0, piles
// Binary search for the insertion position
for left < right {
mid := (left + right) / 2
if top[mid] >= poker {
right = mid
} else {
left = mid + 1
}
}
if left == piles {
piles++
}
// Place this card on the top of the pile
top[left] = poker
}
// The number of piles is the length of the LIS
return piles
}var maxEnvelopes = function(envelopes) {
let n = envelopes.length;
// Sort by width in ascending order, and if widths are
// the same, sort by height in descending order
envelopes.sort((a, b) => {
return a[0] === b[0] ? b[1] - a[1] : a[0] - b[0];
});
// Find the LIS for the height array
let height = new Array(n);
for (let i = 0; i < n; i++) {
height[i] = envelopes[i][1];
}
return lengthOfLIS(height);
};
// Return the length of the LIS in nums
var lengthOfLIS = function(nums) {
let piles = 0, n = nums.length;
let top = new Array(n);
for (let i = 0; i < n; i++) {
// The poker card to be processed
let poker = nums[i];
let left = 0, right = piles;
// Binary search for the insertion position
while (left < right) {
let mid = Math.floor((left + right) / 2);
if (top[mid] >= poker)
right = mid;
else
left = mid + 1;
}
if (left === piles) piles++;
// Place this card on the top of the pile
top[left] = poker;
}
// The number of piles is the length of the LIS
return piles;
};Algorithm Visualization
To reuse the previous function, I have divided the code into two functions. You can also merge the code to save space on the height array.
Due to the addition of test cases, the lengthOfLIS function using binary search must be used to pass all test cases. In this way, the algorithm's time complexity is , as both sorting and calculating the Longest Increasing Subsequence (LIS) require time, resulting in a combined complexity of . The space complexity is , because the function that calculates the LIS requires a top array.