Classic DP: Game Theory

In the previous article Several Brain Teasers, we discussed an interesting "Stone Game." Given the constraints of the problem, the first player is guaranteed to win. However, brain teasers are just that—brain teasers. Real algorithm problems can't be solved by mere clever tricks. Therefore, in this article, we will use the Stone Game to explain how to solve problems of the type "if both players are sufficiently smart, who will win" using dynamic programming algorithms.

The approach to game theory problems is quite similar. The following explanation is based on the ideas from this YouTube video. The core idea is to use tuples to store the results of both players' games on a two-dimensional dp array. Once you master this technique, when someone asks you about problems like pirates dividing gems or two people taking coins, you can simply say: "I'm too lazy to think, let me just write an algorithm to figure it out."

We generalize LeetCode problem #877 "Stone Game" to make it more universal:

You and your friend are facing a row of stone piles, represented by an array piles, where piles[i] indicates the number of stones in the i-th pile. You take turns picking stones, one pile at a time, but you can only take the pile from either the leftmost or rightmost end. The player with the most stones after all piles are taken wins.

The number of piles and the total number of stones can be any positive integers, which can break the scenario where the first player always wins. For example, with three piles piles = [1, 100, 3], whether the first player picks 1 or 3, the decisive 100 stones will be taken by the second player, who will win.

Assuming both players are very smart, write a stoneGame function that returns the difference between the final scores (total number of stones) of the first and second players. For the example above, the first player can get 4 points, and the second player will get 100 points, so your algorithm should return -96:

int stoneGame(int[] nums);

This generalization transforms the problem into a more challenging dynamic programming question. LeetCode problem #486 "Predict the Winner" is a similar problem:

Input: nums = [1,5,2]
Output: false
Explanation: Initially, player 1 can choose between 1 and 2. 
If he chooses 2 (or 1), then player 2 can choose from 1 (or 2) and 5. If player 2 chooses 5, then player 1 will be left with 1 (or 2). 
So, final score of player 1 is 1 + 2 = 3, and player 2 is 5. 
Hence, player 1 will never be the winner and you need to return false.

Input: nums = [1,5,233,7]
Output: true
Explanation: Player 1 first chooses 1. Then player 2 has to choose between 5 and 7. No matter which number player 2 choose, player 1 can choose 233.
Finally, player 1 has more score (234) than player 2 (12), so you need to return True representing player1 can win.

The function signature is as follows:

boolean predictTheWinner(int[] nums);

bool predictTheWinner(vector<int>& nums);

def predictTheWinner(nums: List[int]) -> bool:

func predictTheWinner(nums []int) bool

var predictTheWinner = function(nums) {}

So, if we have a stoneGame function that calculates the difference between the first and second player's scores, the solution to this problem becomes straightforward:

public boolean predictTheWinner(int[] nums) {
    // If the score of the first player is greater
    // than or equal to the second player, they can
    return stoneGame(nums) >= 0;
}

bool predictTheWinner(vector<int>& nums) {
    // if the score of the first player is greater
    // than or equal to the second player, they can
    return stoneGame(nums) >= 0;
}

def predictTheWinner(nums):
    # if the score of the first player is greater
    # than or equal to the second player, they can
    return stoneGame(nums) >= 0

func predictTheWinner(nums []int) bool {
    // if the score of the first player is greater
    // than or equal to the second player, they can
    return stoneGame(nums) >= 0
}

var predictTheWinner = function(nums) {
    // if the score of the first player is greater
    // than or equal to the second player, they can
    return stoneGame(nums) >= 0;
}

How should the stoneGame function be written? The challenge in game theory problems is that two players take turns making decisions, and both are extremely clever. How can this process be represented in programming? It's actually not difficult. Following the routine emphasized multiple times in the Core Framework of Dynamic Programming, first clearly define the meaning of the dp array. Once you identify the "states" and "choices," everything will fall into place.

1. Defining the Meaning of the dp Array

Defining the meaning of the dp array requires a lot of technical skill. A single problem may have multiple ways of defining it, and different definitions will lead to different state transition equations. However, as long as the logic is correct, the same answer can ultimately be achieved.

I recommend not getting too attached to solutions that seem impressive but have very concise code. It's best to be steady and adopt a solution that is easily interpretable and most generalizable. This article provides a general design framework for game theory problems.

Before introducing the meaning of the dp array, let's first look at what the dp array will ultimately look like:

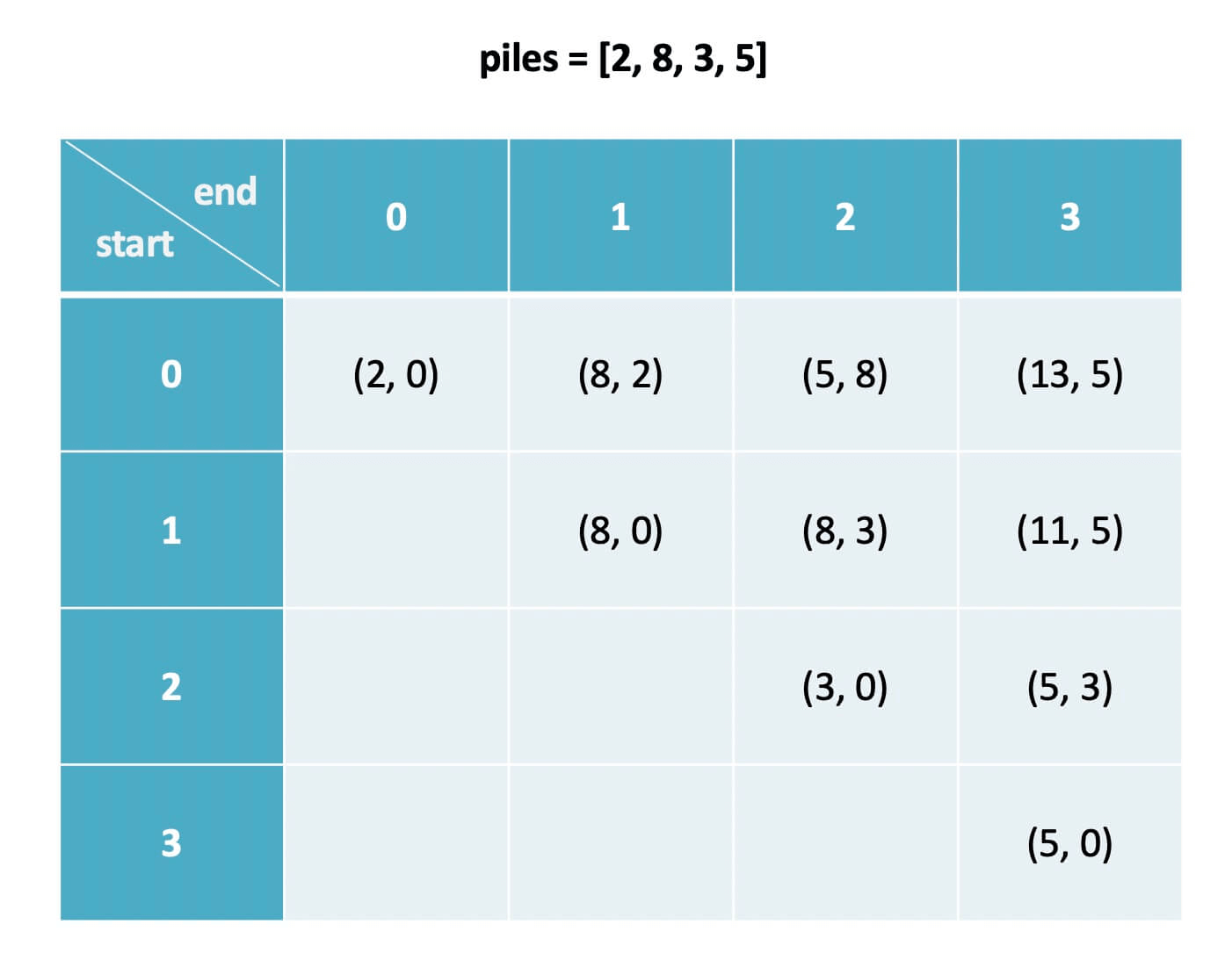
In the following explanation, a tuple is considered a class containing first and second attributes. To save space, these attributes are abbreviated as fir and sec. For example, with the data from the image above, we say dp[1][3].fir = 11 and dp[0][1].sec = 2.

First, let's address some questions readers might have:

How do you represent tuples in this 2D dp table programmatically? Why is half of this dp table unused, and how can it be optimized? The answer is simple: don't worry about these details for now. Focus on understanding the problem-solving approach first.

Here's an explanation of the dp array's meaning:

dp[i][j].fir = x means that for the stone piles piles[i...j], the maximum score the first player can achieve is x.

dp[i][j].sec = y means that for the stone piles piles[i...j], the maximum score the second player can achieve is y.

To illustrate, let's assume piles = [2, 8, 3, 5] with indices starting from 0. Then:

dp[0][1].fir = 8 implies that for the stone piles [2, 8], the first player can score up to 8 points. dp[1][3].sec = 5 implies that for the stone piles [8, 3, 5], the second player can score up to 5 points.

What we want to find is the difference between the final scores of the first and second players. According to this definition, it is dp[0][n-1].fir - dp[0][n-1].sec, which means the difference between the optimal scores of the first and second players when facing the entire piles.

II. State Transition Equation

Writing the state transition equation is straightforward. First, identify all the "states" and the "choices" available for each state, then choose the optimal one.

Based on the previous definition of the dp array, there are clearly three states: the starting index i, the ending index j, and the current player.

dp[i][j][fir or sec]
where:
0 <= i < piles.length
i <= j < piles.length

For each state in this problem, there are two choices: pick the leftmost pile of stones or the rightmost pile of stones. We can enumerate all states like this:

n = piles.length
for 0 <= i < n:
    for j <= i < n:
        for who in {fir, sec}:
            dp[i][j][who] = max(left, right)

The pseudocode above provides a general framework for dynamic programming. The challenge in this problem is that both players are sufficiently smart and take turns making choices, meaning the first player's choice affects the second player. How do we express this?

Based on our definition of the dp array, it's easy to overcome this challenge and write the state transition equation:

dp[i][j].fir = max(piles[i] + dp[i+1][j].sec, piles[j] + dp[i][j-1].sec)
dp[i][j].fir = max(     选择最左边的石头堆     ,     选择最右边的石头堆      )
# Explanation: As the first player, when facing piles[i...j], I have two choices:

# Either I choose the leftmost pile piles[i], making the situation piles[i+1...j],
# then it's the opponent's turn, I become the second player,
# and my optimal score as the second player is dp[i+1][j].sec

# Or I choose the rightmost pile piles[j], making the situation piles[i...j-1]
# then it's the opponent's turn, I become the second player,
# and my optimal score as the second player is dp[i][j-1].sec

if 先手选择左边:
    dp[i][j].sec = dp[i+1][j].fir
if 先手选择右边:
    dp[i][j].sec = dp[i][j-1].fir
# Explanation: As the second player, I wait for the
# first player to choose first, there are two

# If the first player chooses the leftmost pile, leaving me with piles[i+1...j]
# now it's my turn, I become the first player, and my
# optimal score as the first player is dp[i+1][j].fir

# If the first player chooses the rightmost pile, leaving me with piles[i...j-1]
# now it's my turn, I become the first player, and my
# optimal score as the first player is dp[i][j-1].fir

According to the definition of the dp array, we can also identify the base case, which is the simplest scenario:

dp[i][j].fir = piles[i]
dp[i][j].sec = 0
其中 0 <= i == j < n
# Explanation: i and j being equal means there is only one pile of stones piles[i] in front
# Obviously, the score of the first player is piles[i]
# The second player has no stones to take, so the score is 0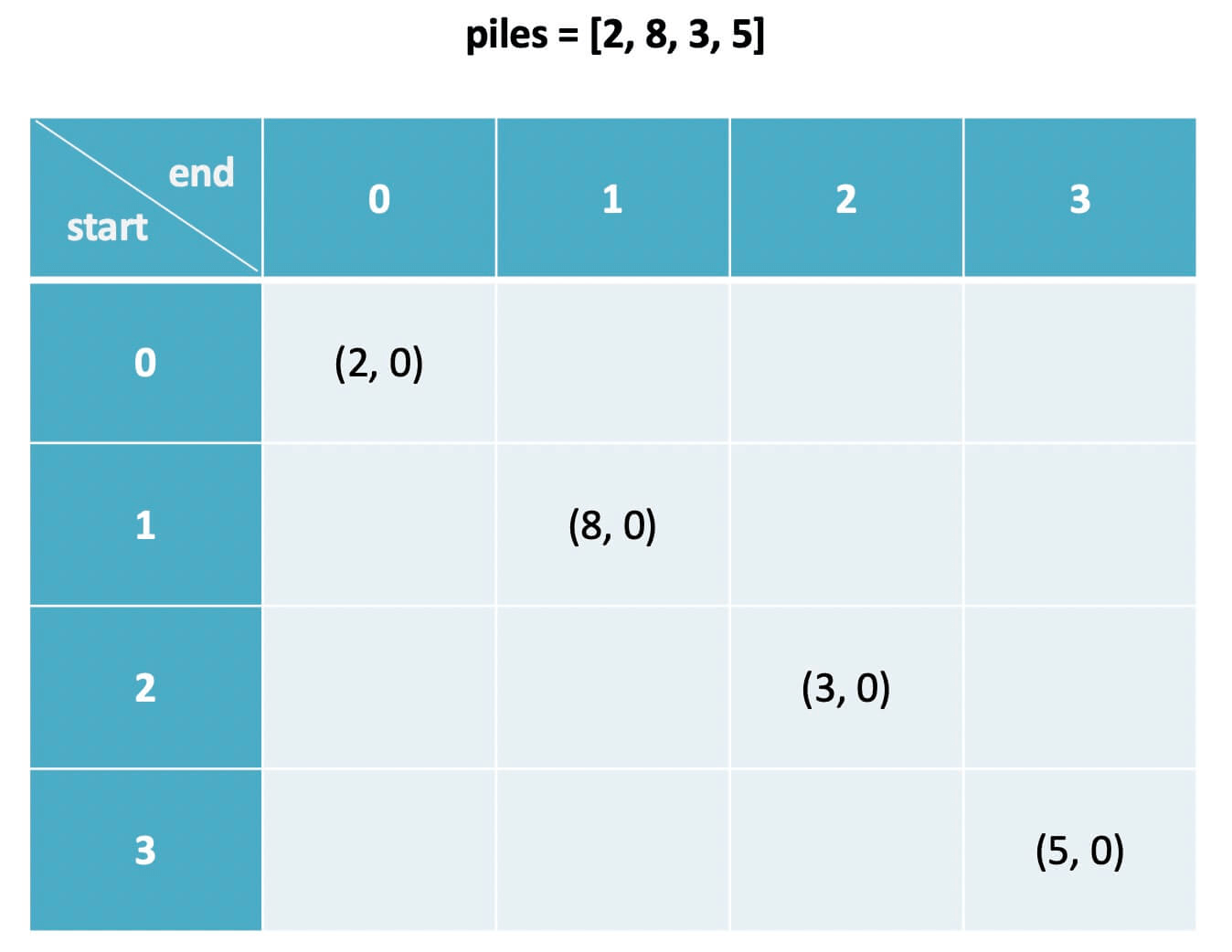

Here, it is important to note that we find the base case is diagonal, and when calculating dp[i][j], we need dp[i+1][j] and dp[i][j-1]:

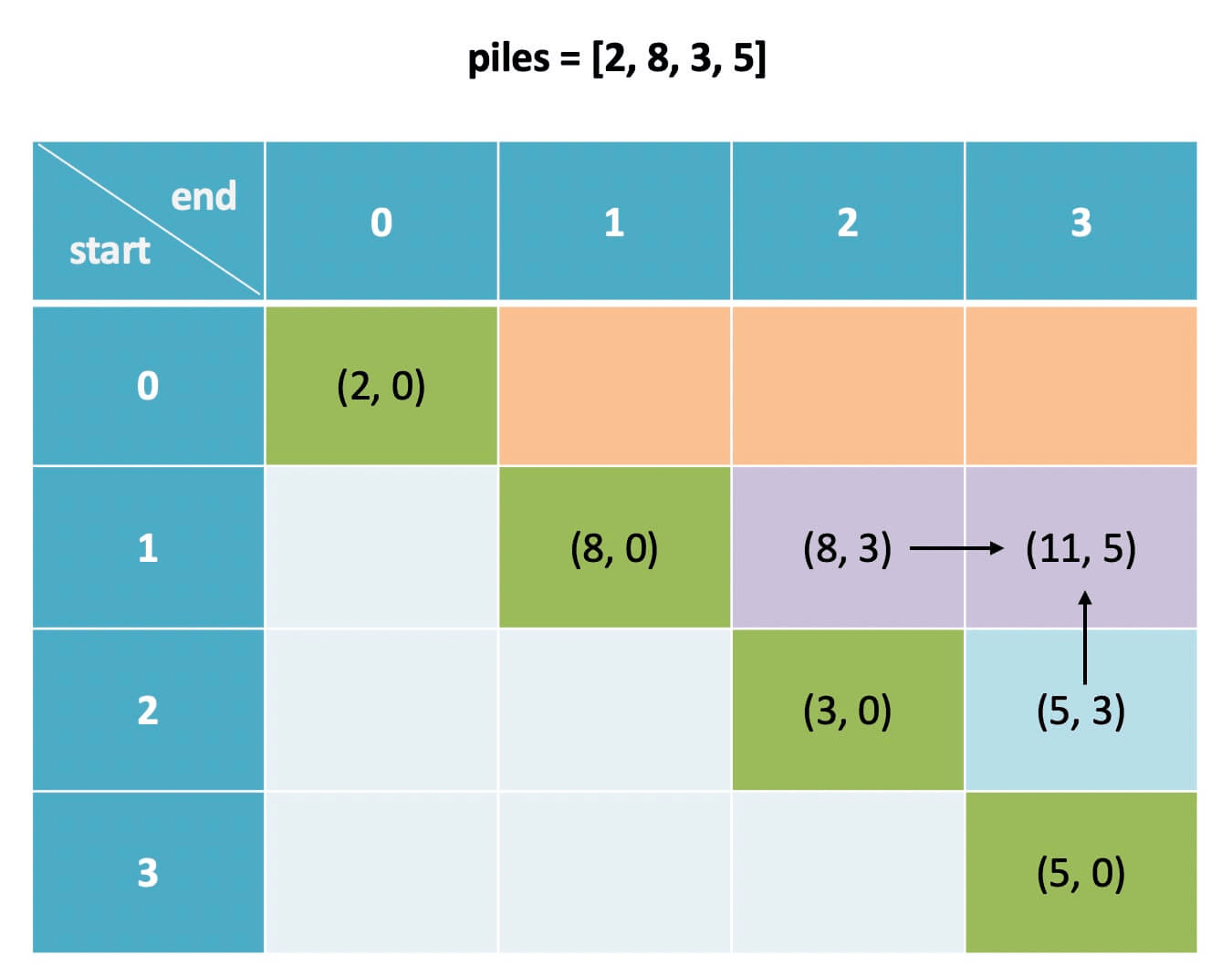
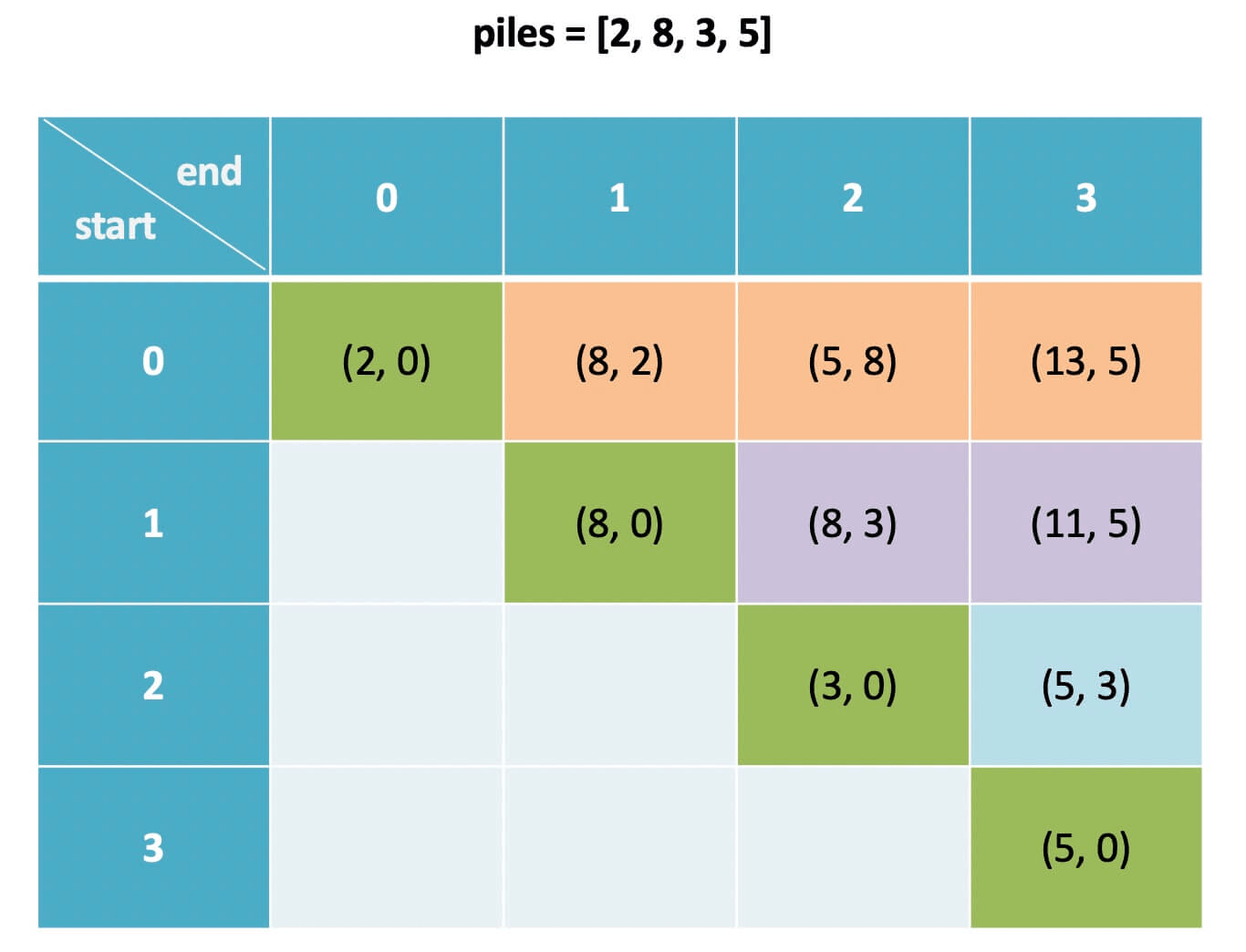
According to the principle of determining the traversal direction of the dp array from the previous article Dynamic Programming Q&A, the algorithm should traverse the dp array backward:

for (int i = n - 2; i >= 0; i--) {
    for (int j = i + 1; j < n; j++) {
        dp[i][j] = ...
    }
}

3. Code Implementation

How can we implement the fir and sec tuple? You can use Python, which has a built-in tuple type; or use C++'s pair container; or use a three-dimensional array dp[n][n][2], where the last dimension acts as a tuple; or we can write a Pair class ourselves:

class Pair {
    int fir, sec;
    Pair(int fir, int sec) {
        this.fir = fir;
        this.sec = sec;
    }
}

class Pair {
public:
    int fir, sec;
    Pair(int fir, int sec) {
        this->fir = fir;
        this->sec = sec;
    }
};

class Pair:
    def __init__(self, fir: int, sec: int):
        self.fir = fir
        self.sec = sec

type Pair struct {
    fir int
    sec int
}

func NewPair(fir int, sec int) *Pair {
    return &Pair{fir, sec}
}

function Pair(fir, sec) {
    this.fir = fir;
    this.sec = sec;
}

Then, we can directly translate our state transition equation into code. Note that we need to traverse the array in reverse order:

// Return the score difference between the first and second player at the end of the game
int stoneGame(int[] piles) {
    int n = piles.length;
    // Initialize the dp array
    Pair[][] dp = new Pair[n][n];
    for (int i = 0; i < n; i++) 
        for (int j = i; j < n; j++)
            dp[i][j] = new Pair(0, 0);
    // Fill in the base case
    for (int i = 0; i < n; i++) {
        dp[i][i].fir = piles[i];
        dp[i][i].sec = 0;
    }

    // Traverse the array in reverse order
    for (int i = n - 2; i >= 0; i--) {
        for (int j = i + 1; j < n; j++) {
            // The first player chooses the score from the leftmost or rightmost
            int left = piles[i] + dp[i+1][j].sec;
            int right = piles[j] + dp[i][j-1].sec;
            // Apply the state transition equation
            // The first player will definitely choose the larger
            // result, and the second player's choice will change
            if (left > right) {
                dp[i][j].fir = left;
                dp[i][j].sec = dp[i+1][j].fir;
            } else {
                dp[i][j].fir = right;
                dp[i][j].sec = dp[i][j-1].fir;
            }
        }
    }
    Pair res = dp[0][n-1];
    return res.fir - res.sec;
}

#include <iostream>
#include <algorithm>
using namespace std;
class Pair {
public:
    int fir, sec;
    Pair(int fir, int sec) {
        this->fir = fir;
        this->sec = sec;
    }
};

// Return the difference in scores between the first and second players at the end of the game
int stoneGame(vector<int>& piles) {
    int n = piles.size();
    // Initialize the dp array
    vector<vector<Pair>> dp(n, vector<Pair>(n, Pair(0, 0)));
    // Fill in the base case
    for (int i = 0; i < n; i++) {
        dp[i][i].fir = piles[i];
        dp[i][i].sec = 0;
    }

    // Traverse the array in reverse
    for (int i = n - 2; i >= 0; i--) {
        for (int j = i + 1; j < n; j++) {
            // The first player chooses the score from the leftmost or rightmost
            int left = piles[i] + dp[i+1][j].sec;
            int right = piles[j] + dp[i][j-1].sec;
            // Apply the state transition equation
            // The first player will definitely choose the larger
            // result, and the second player's choice will change
            if (left > right) {
                dp[i][j].fir = left;
                dp[i][j].sec = dp[i+1][j].fir;
            } else {
                dp[i][j].fir = right;
                dp[i][j].sec = dp[i][j-1].fir;
            }
        }
    }
    Pair res = dp[0][n-1];
    return res.fir - res.sec;
}

# Return the difference in scores between the first and second players at the end of the game
def stoneGame(piles: List[int]) -> int:
    n = len(piles)
    # Initialize the dp array
    dp = [[Pair(0, 0) for _ in range(n)] for _ in range(n)]
    for i in range(n): 
        for j in range(i, n):
            dp[i][j] = Pair(0, 0)
    # Fill in the base case
    for i in range(n):
        dp[i][i].fir = piles[i]
        dp[i][i].sec = 0

    # Traverse the array in reverse
    for i in range(n - 2, -1, -1):
        for j in range(i + 1, n):
            # The first player chooses the score from the leftmost or rightmost
            left = piles[i] + dp[i+1][j].sec
            right = piles[j] + dp[i][j-1].sec
            # Apply the state transition equation
            # The first player will definitely choose the larger
            # result, and the second player's choice will change
            if left > right:
                dp[i][j].fir = left
                dp[i][j].sec = dp[i+1][j].fir
            else:
                dp[i][j].fir = right
                dp[i][j].sec = dp[i][j-1].fir

    res = dp[0][n-1]
    return res.fir - res.sec

// Return the difference in scores between the first and second players at the end of the game
func stoneGame(piles []int) int {
    n := len(piles)
    // Initialize the dp array
    dp := make([][]Pair, n)
    for i := 0; i < n; i++ {
        dp[i] = make([]Pair, n)
        for j := 0; j < n; j++ {
            dp[i][j] = Pair{0, 0}
        }
    }
    // Fill in the base case
    for i := 0; i < n; i++ {
        dp[i][i].fir = piles[i]
        dp[i][i].sec = 0
    }

    // Traverse the array in reverse
    for i := n - 2; i >= 0; i-- {
        for j := i + 1; j < n; j++ {
            // The first player chooses the score from the leftmost or rightmost
            left := piles[i] + dp[i+1][j].sec
            right := piles[j] + dp[i][j-1].sec
            // Apply the state transition equation
            // The first player will definitely choose the larger
            // result, and the second player's choice will change
            if left > right {
                dp[i][j].fir = left
                dp[i][j].sec = dp[i+1][j].fir
            } else {
                dp[i][j].fir = right
                dp[i][j].sec = dp[i][j-1].fir
            }
        }
    }

    res := dp[0][n-1]
    return res.fir - res.sec
}

var stoneGame = function(piles) {
    const n = piles.length;
    // initialize the dp array
    const dp = new Array(n).fill(0).map(() => new Array(n).fill(0).map(() => new Pair(0, 0)));
    // fill in the base case
    for (let i = 0; i < n; i++) {
        dp[i][i].fir = piles[i];
        dp[i][i].sec = 0;
    }

    // traverse the array in reverse order
    for (let i = n - 2; i >= 0; i--) {
        for (let j = i + 1; j < n; j++) {
            // the first player chooses the score from the leftmost or rightmost
            const left = piles[i] + dp[i+1][j].sec;
            const right = piles[j] + dp[i][j-1].sec;
            // apply the state transition equation
            // the first player will definitely choose the larger
            // result, and the second player's choice will change
            if (left > right) {
                dp[i][j].fir = left;
                dp[i][j].sec = dp[i+1][j].fir;
            } else {
                dp[i][j].fir = right;
                dp[i][j].sec = dp[i][j-1].fir;
            }
        }
    }

    const res = dp[0][n-1];
    return res.fir - res.sec;
};

The dynamic programming solution can be confusing without the guidance of a state transition equation. However, with the detailed explanation provided earlier, readers should be able to clearly understand the meaning of this chunk of code.

Moreover, notice that calculating dp[i][j] only depends on its left and bottom elements. This indicates there is room for optimization by converting it into a one-dimensional dp array. Imagine flattening the two-dimensional plane, projecting it onto one dimension. However, a one-dimensional dp is more complex and less interpretable, so it's not worth spending time to understand it.

IV. Final Summary

This article presents a dynamic programming solution to game theory problems. Typically, these problems involve two intelligent players. The general approach to describe such games in programming is using a two-dimensional dp array, where tuples represent the optimal decisions for both players.

This design is chosen because after the first player makes a choice, they become the second player, and after the second player makes their choice, they become the first player again. This role switch allows us to reuse previous results, a classic hallmark of dynamic programming.

By this point, readers should grasp the pattern of using algorithms to solve game theory problems. When learning algorithms, focus on the template frameworks rather than seemingly brilliant ideas. Don't expect to write the optimal solution right away. Don't hesitate to use more space, avoid premature optimization, and don't be afraid of multi-dimensional arrays. The dp array is there to store information and avoid redundant calculations, so use it freely until you are satisfied.